Gated Recurrent Unit Network of Particle Swarm Optimization for Drifting Buoy Trajectory Prediction
-
摘要: 该文针对漂流浮标的轨迹预测问题,提出一种基于深度学习框架的端对端预测模型。由于不同海域的水动力模型存在较大差异,针对海面漂流浮标的流体载荷计算也较为复杂。因此,该文根据漂流浮标历史轨迹形成的多维时间序列,提出更具有普适性的基于数据驱动的轨迹预测模型。该模型将粒子群优化算法(PSO)与门控循环单元(GRU)结合,使用PSO算法对GRU神经网络的超参数进行初始化,经过多次迁移迭代训练后获得最优漂流浮标轨迹预测模型。最后使用多个北大西洋真实漂流浮标轨迹数据进行验证,结果表明PSOGRU算法能够实现准确的漂流浮标轨迹预测。Abstract: Considering the trajectory prediction problem of drift buoys, an end-to-end prediction model based on the depth learning framework is proposed in this paper.The hydrodynamic models in different sea areas are quite different, and the calculation of fluid load of floating buoys on the sea surface is also complicated. Therefore, a more universal data-driven trajectory prediction model based on the multidimensional time series formed by the historical trajectories of drifting buoys is proposed. In this model, Particle Swarm Optimization (PSO) is combined with Gated Recurrent Unit (GRU), and the PSO is used to initialize the hyperparameters of the GRU neural network. The optimal drifting buoy trajectory prediction model is obtained after multiple migration iteration training. Finally, several real drifting buoy track data in the North Atlantic are used to verify the results. The results show that the PSOGRU algorithm can achieve accurate drifting buoy track prediction results.
-
表 1 4只漂流浮标轨迹预测的网络模型超参数最优解
神经网络超参数 1号浮标 2号浮标 3号浮标 4号浮标 初始化中间层神经元个数$\lambda $ 50 35 32 13 初始学习率$\alpha $ 0.05 0.05 0.04 0.03 表 2 7种模型对4只漂流浮标72 h漂流轨迹预测的ADE结果(m)
模型 1号浮标 2号浮标 3号浮标 4号浮标 平均值 卡尔曼滤波 180.93 506.72 472.33 332.75 373.18 无迹卡尔曼滤波 99.51 198.73 169.62 106.99 143.71 LSTM神经网络 141.43 495.79 191.99 140.63 242.46 GRU神经网络 95.51 434.04 107.20 135.18 192.98 Transformer网络 100.24 418.28 83.22 223.17 185.42 PSOLSTM网络模型 136.95 369.35 88.98 155.42 187.68 PSOGRU网络模型 50.79 152.21 79.72 101.87 96.15 表 3 7种模型对4只漂流浮标72小时漂流轨迹预测的FDE结果(m)
模型 1号浮标 2号浮标 3号浮标 4号浮标 平均值 卡尔曼滤波 2 604.10 2 919.93 7 157.77 3 850.37 4 133.04 无迹卡尔曼滤波 723.83 1 456.09 2 844.72 683.77 1 427.10 LSTM神经网络 2 844.00 1 659.31 1 280.71 2 409.21 2 048.31 GRU神经网络 2 433.24 1 283.96 1 443.72 2 045.37 1 801.58 Transformer网络 2 064.30 3 776.45 929.65 3 594.53 2 591.23 PSOLSTM网络模型 2 122.79 1 477.55 1 124.07 1 269.57 1 498.50 PSOGRU网络模型 980.05 791.39 774.96 807.41 838.45 表 4 7种模型下的预测时间对比(s)
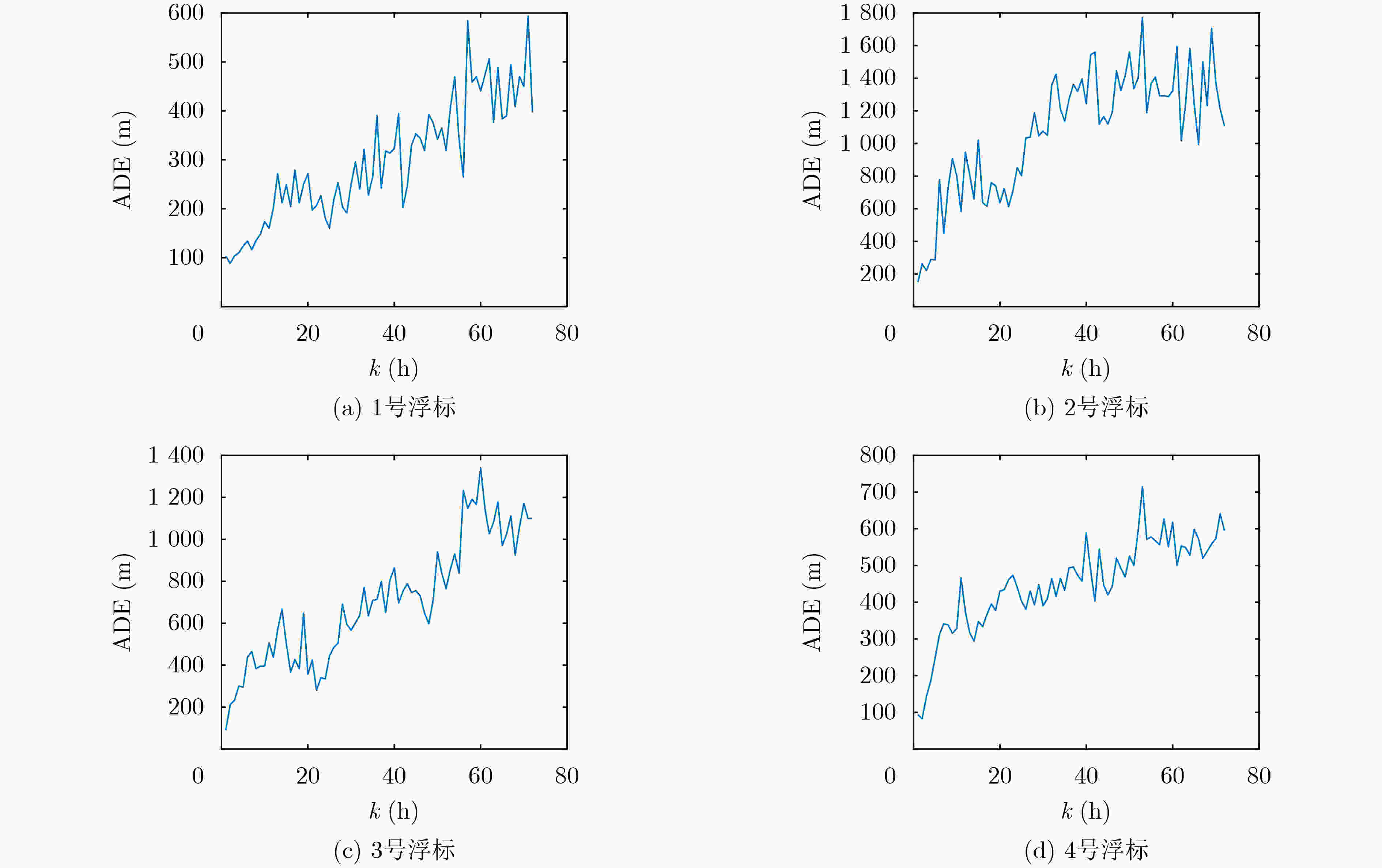
模型 1号浮标 2号浮标 3号浮标 4号浮标 平均预测时间 卡尔曼滤波 0.017 0.017 0.016 0.015 0.016 无迹卡尔曼滤波 0.017 0.017 0.016 0.015 0.016 LSTM神经网络 1 425.01 1 425.73 1 425.72 1 425.03 1 425.37 GRU神经网络 972.74 969.91 969.90 974.18 971.68 Transformer网络 834.44 836.43 846.26 836.25 838.35 PSOLSTM网络模型 929.43 927.31 927.30 928.03 928.02 PSOGRU网络模型 641.88 636.21 636.91 641.19 639.05 表 5 ADE(m)最值对应的预测时间k (h)
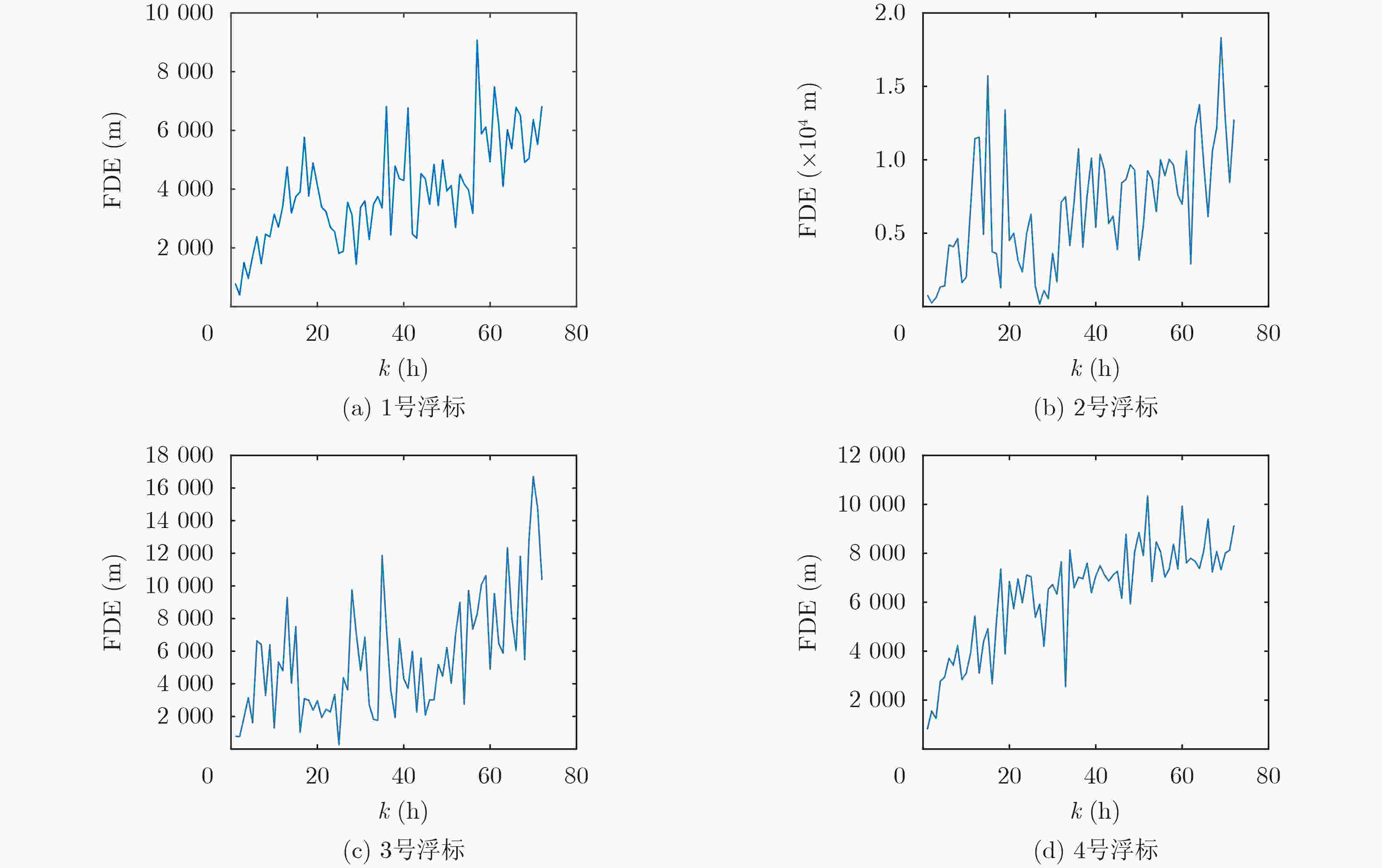
1号浮标 2号浮标 3号浮标 4号浮标 最大值 593.18 k = 71 1772.63 k = 53 1340.71 k =60 715.01 k =53 最小值 88.17 k = 2 149.66 k = 1 90.23 k =1 83.15 k =2 表 6 FDE (m)最值对应的预测时间k (h)
1号浮标 2号浮标 3号浮标 4号浮标 最大值 9 074.36 k =57 18 316.02 k =69 16 694.51 k =70 10 343.81 k =52 最小值 399.34 k =2 174.82 k =27 257.29 k =25 807.41 k =1 -
[1] 蔡树群, 张文静, 王盛安. 海洋环境观测技术研究进展[J]. 热带海洋学报, 2007, 26(3): 76–81. doi: 10.3969/j.issn.1009-5470.2007.03.014.CAI Shuqun, ZHANG Wenjing, and WANG Sheng’an. An advance in marine environment observation technology[J]. Journal of Tropical Oceanography, 2007, 26(3): 76–81. doi: 10.3969/j.issn.1009-5470.2007.03.014. [2] ZHAO Zhiqiang. Research on monitoring technology of marine oil spill environment based on LoT+GIS[C]. 2022 International Conference on Educational Informatization, E-commerce and Information System, Macao, China, 2022: 134–138. doi: 10.25236/iceieis.2022.031. [3] WANG Wei, SU Jintao, YU Xiaohong, et al. Research on attitude stability of AUV towed communication buoy[C]. 2022 IEEE 6th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Beijing, China, 2022: 1450–1455. doi: 10.1109/IAEAC54830.2022.9929985. [4] ROH H, JOE H, and YU S C. Modeling trajectory characteristic of moor-less buoy system under ocean current[C]. 2016 IEEE/OES Autonomous Underwater Vehicles (AUV), Tokyo, Japan, 2016: 307–310. doi: 10.1109/AUV.2016.7778688. [5] ZHU Kui, MU Lin, and XIA Xiaoyu. An ensemble trajectory prediction model for maritime search and rescue and oil spill based on sub-grid velocity model[J]. Ocean Engineering, 2021, 236: 109513. doi: 10.1016/j.oceaneng.2021.109513. [6] 龙绍桥, 娄安刚, 谭海涛, 等. 海上溢油粒子追踪预测模型中的两种数值方法比较[J]. 中国海洋大学学报, 2006, 36(S): 157–162. doi: 10.3969/j.issn.1672-5174.2006.z1.031.LONG Shaoqiao, LOU Angang, TAN Haitao, et al. Comparison of two numerical methods for solving the model for oil spill particle trajectory on the sea[J]. Periodical of Ocean University of China, 2006, 36(S): 157–162. doi: 10.3969/j.issn.1672-5174.2006.z1.031. [7] TENG Fei, DING Zhaohao, HU Zechun, et al. Technical review on advanced approaches for electric vehicle charging demand management, part I: Applications in electric power market and renewable energy integration[J]. IEEE Transactions on Industry Applications, 2020, 56(5): 5684–5694. doi: 10.1109/TIA.2020.2993991. [8] CHEN Shuo, LIN Rongheng, and ZENG Wei. Short-term load forecasting method based on ARIMA and LSTM[C]. 2022 IEEE 22nd International Conference on Communication Technology (ICCT), Nanjing, China, 2022: 1913–1917. doi: 10.1109/ICCT56141.2022.10073051. [9] ZHANG Jing, WU Yingnian, and JIAO Shuai. Research on trajectory tracking algorithm based on LSTM-UKF[C]. 2021 7th IEEE International Conference on Network Intelligence and Digital Content (IC-NIDC), Beijing, China, 2021: 61–65. doi: 10.1109/IC-NIDC54101.2021.9660592. [10] XING Yang, LV Chen, and CAO Dongpu. Personalized vehicle trajectory prediction based on joint time-series modeling for connected vehicles[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 1341–1352. doi: 10.1109/TVT.2019.2960110. [11] WU Yuankang, ZHONG Youjing, and PHAN Q T. Overview of day-ahead solar power forecasts based on weather classifications[C]. 2023 IEEE/IAS 59th Industrial and Commercial Power Systems Technical Conference (I&CPS), Las Vegas, USA, 2023: 1–8. doi: 10.1109/ICPS57144.2023.10142132. [12] HELMY I, TARAFDER P, and CHOI W. LSTM-GRU model-based channel prediction for one-bit massive MIMO system[J]. IEEE Transactions on Vehicular Technology, 2023, 72(8): 11053–11057. doi: 10.1109/TVT.2023.3262951. [13] HAN Ping, WANG Wenqing, SHI Qingyan, et al. Real-time short- term trajectory prediction based on GRU neural network[C]. IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, USA, 2019: 1–8. doi: 10.1109/DASC43569.2019.9081618. [14] CHEN Zexuan and WANG Lan. Aircraft trajectory prediction model based on improved GRU structure[C]. 2023 3rd International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 2023: 225–228. doi: 10.1109/ICCECE58074.2023.10135263. [15] AÇIKKAR M and ALTUNKOL Y. A novel hybrid PSO- and GS-based hyperparameter optimization algorithm for support vector regression[J]. Neural Computing and Applications, 2023, 35(27): 19961–19977. doi: 10.1007/s00521-023-08805-5. [16] KALITA D J, SINGH V P, and KUMAR V. A lightweight knowledge-based PSO for SVM hyper-parameters tuning in a dynamic environment[J]. The Journal of Supercomputing, 2023, 79(16): 18777–18799. doi: 10.1007/s11227-023-05385-y. [17] KENNEDY J and EBERHART R. Particle swarm optimization[C]. ICNN’95 - International Conference on Neural Networks, Perth, Australia, 1995: 1942–1948. doi: 10.1109/ICNN.1995.488968. [18] GUPTA A, JOHNSON J, FEI-FEI L, et al. Social GAN: Socially acceptable trajectories with generative adversarial networks[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 2255–2264. doi: 10.1109/CVPR.2018.00240. [19] ALAHI A, GOEL K, RAMANATHAN V, et al. Social LSTM: Human trajectory prediction in crowded spaces[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016: 961–971. doi: 10.1109/CVPR.2016.110. [20] SHI Yuhui and EBERHART R. A modified particle swarm optimizer[C]. 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat No98TH8360), Anchorage, USA, 1998: 69–73. doi: 10.1109/ICEC.1998.699146. [21] CLERC M. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization[C]. The 1999 Congress on Evolutionary Computation-CEC99 (Cat No 99TH8406), Washington, USA, 1999: 1951–1957. doi: 10.1109/CEC.1999.785513. [22] YE Zehao, SONG Yawei, HUA Liangfa, et al. Radar target tracking based on some multi-dimensional adaptive UKF[C]. 2022 2nd International Conference on Frontiers of Electronics, Information and Computation Technologies (ICFEICT), Wuhan, China, 2022: 28–33. doi: 10.1109/ICFEICT57213.2022.00013. -





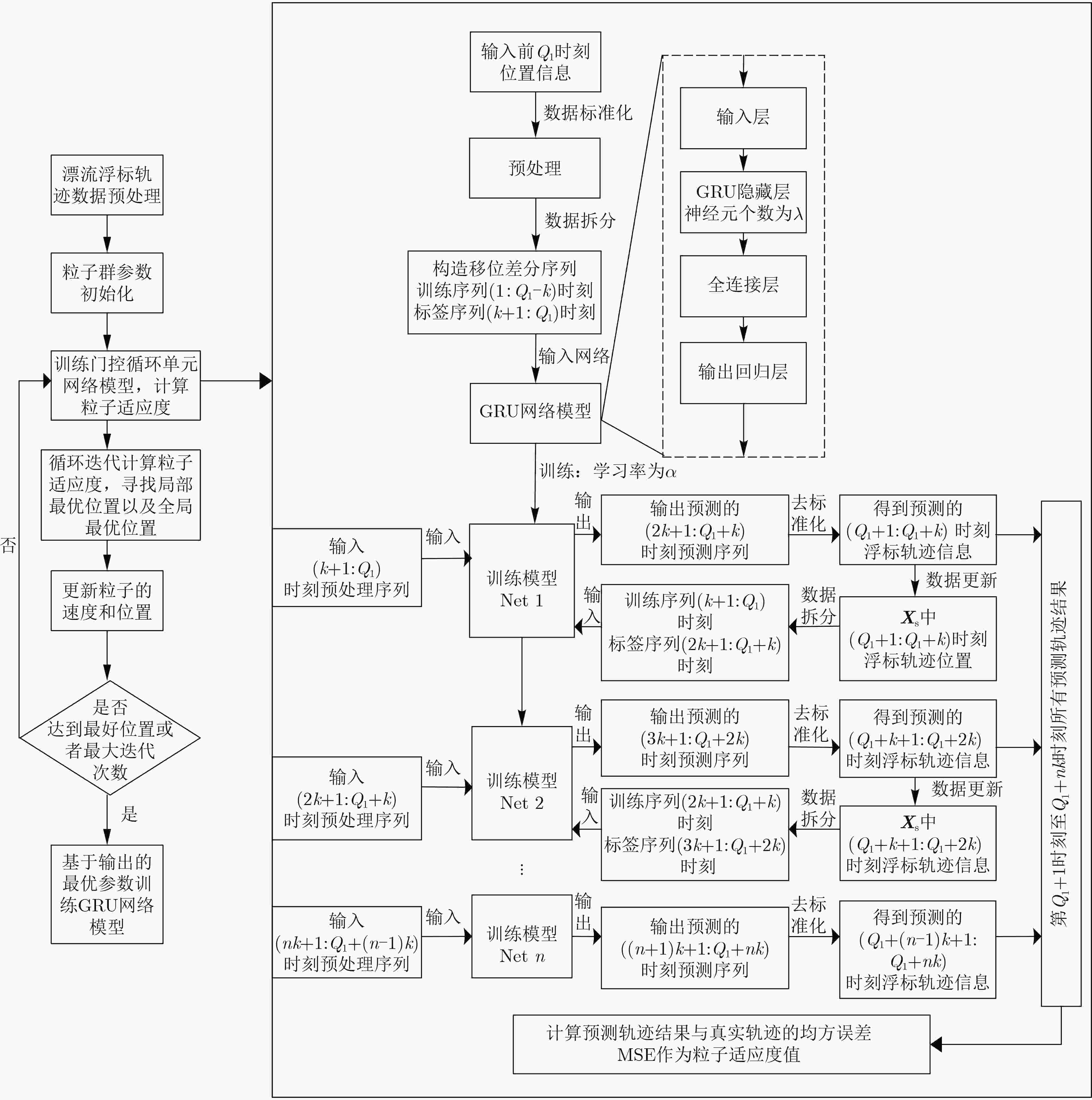
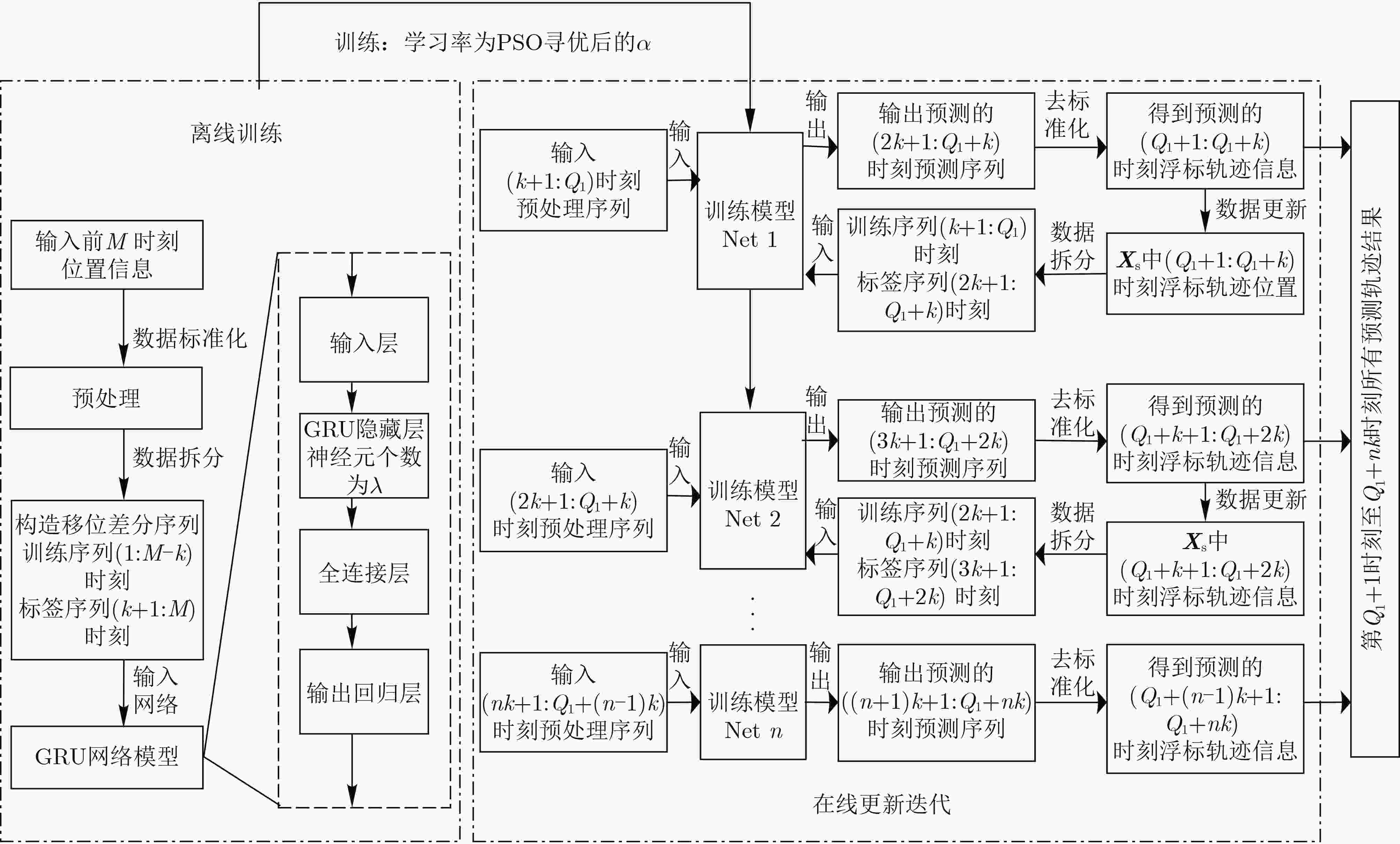
 下载:
下载:
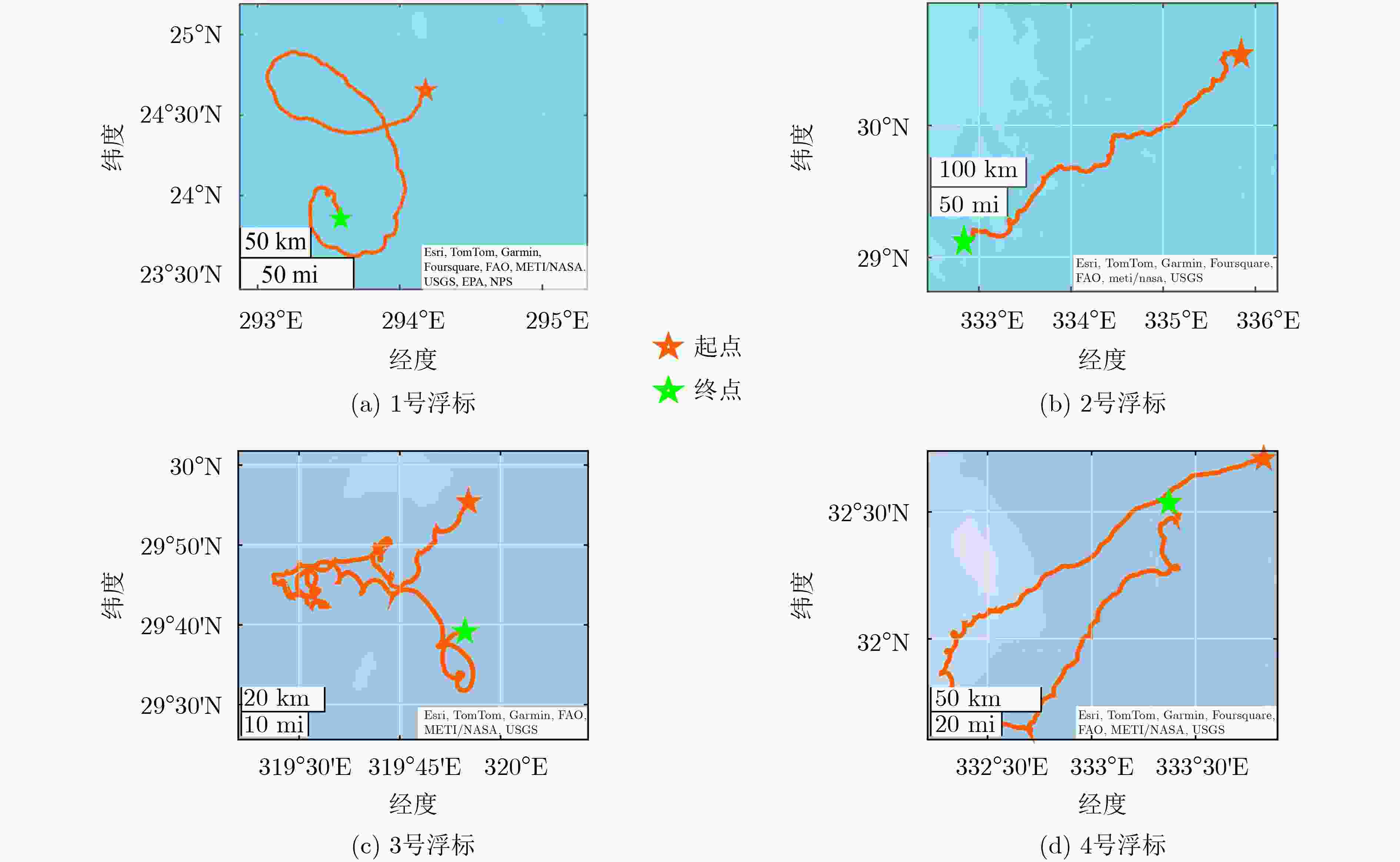



 下载:
下载:
