Anomaly Detection of Small Targets on Sea Surface Based on Deep Graph Infomax
-
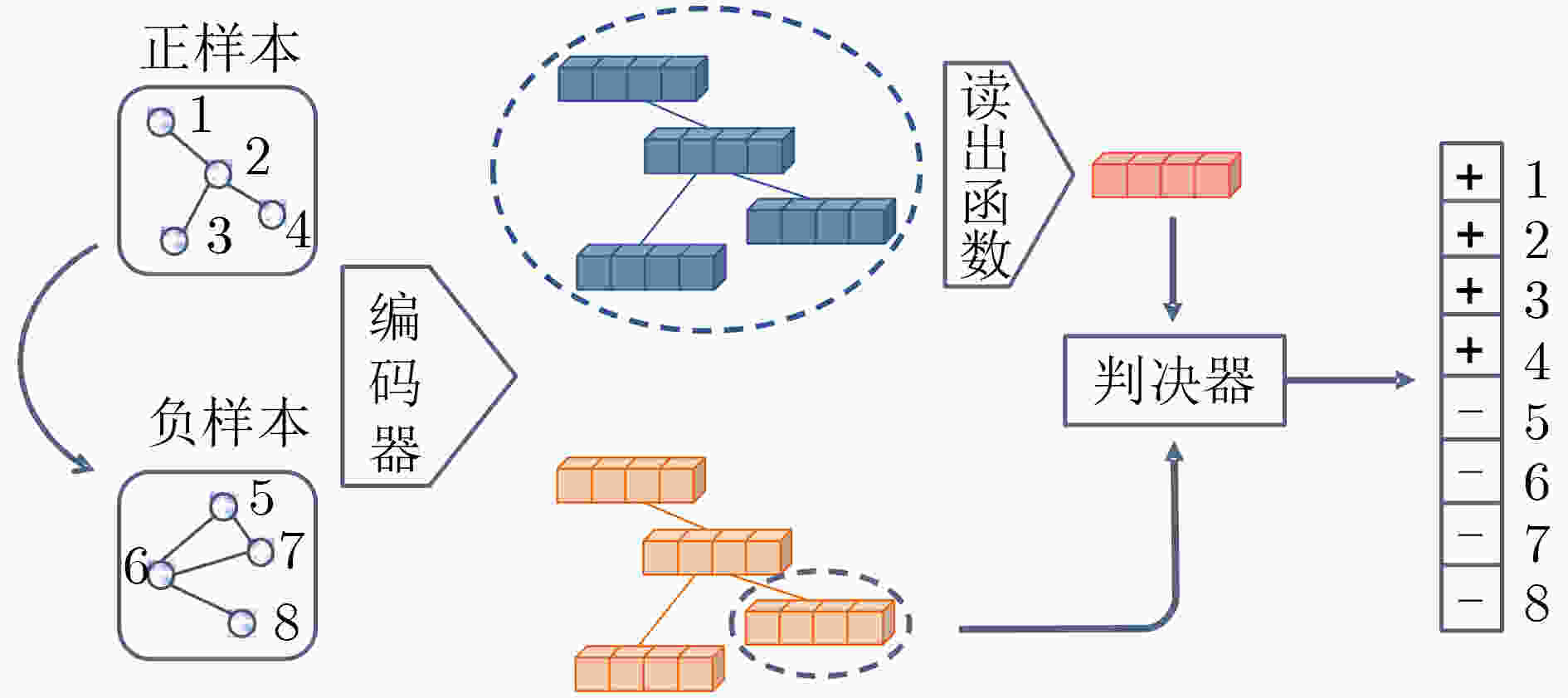
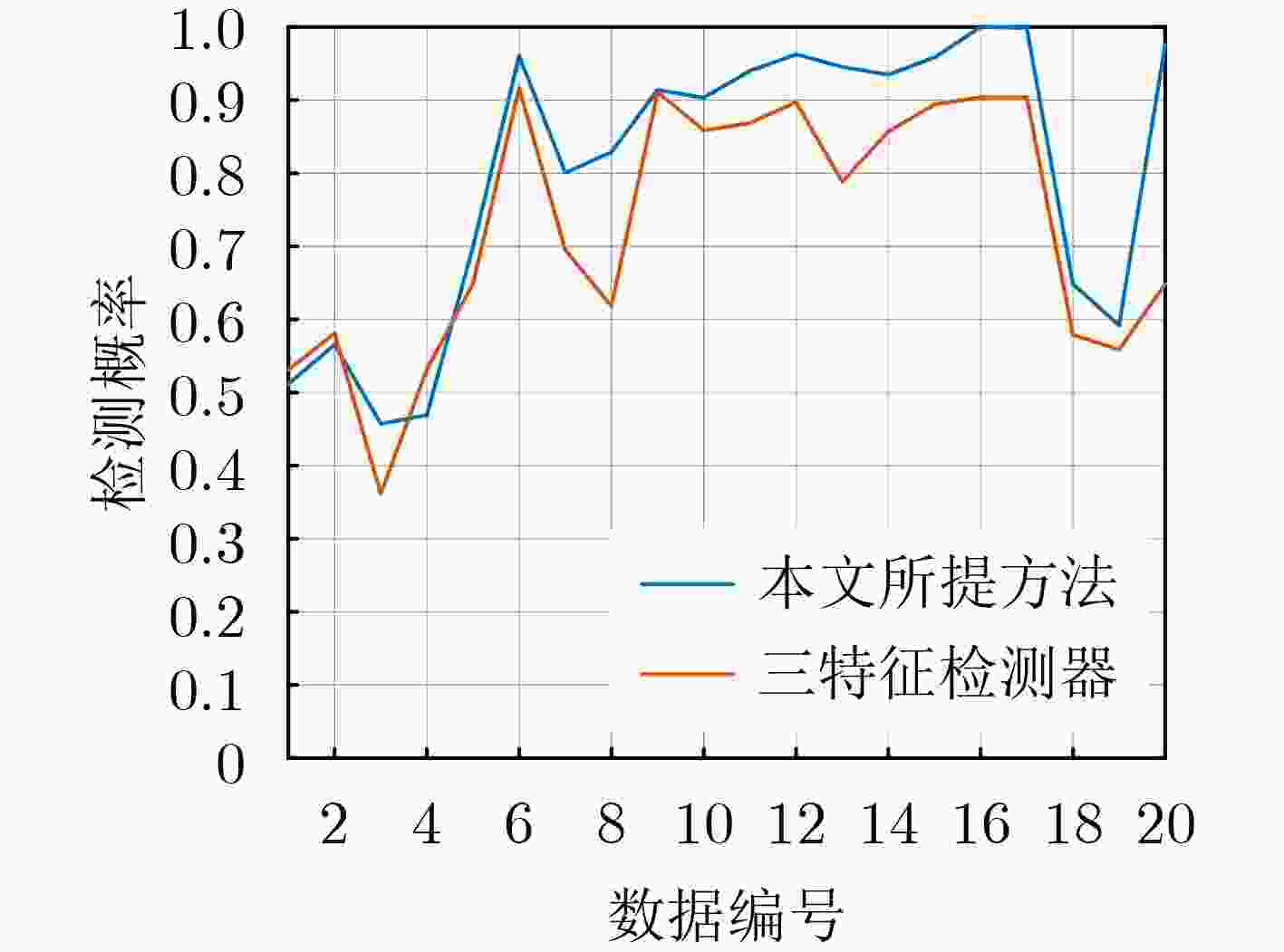
摘要: 受到复杂海洋环境的影响，雷达对海面慢速小目标难以实现高性能检测。对于这类目标，传统的基于能量的统计检测方法存在着严重的性能损失。针对这一问题，该文提出了基于互信息最大化框架下的海面小目标检测方法，实现海杂波背景下的无监督目标异常检测任务。首先，考虑到高分辨雷达回波不满足传统神经网络对样本独立同分布的假设，该文从图的角度重新建模数据，利用回波的空时相关特性来构建图拓扑结构。该文提出相对最大节点度并联合7个已有特征作为节点的初始表示向量。接下来，采用图注意力网络作为互信息最大化框架中的编码器学习节点表示向量。最后，使用异常检测算法进行目标检测，并实现虚警可控。经实测数据验证，使用快速凸包学习算法时，相比三特征检测器，所提检测器性能提升了9.2%；相比时频三特征检测器，性能提升了7.9%。当网络输出更高维的表示向量时，使用孤立森林算法的检测器的性能提升了27.4%。Abstract: Due to the complex marine environment, it is difficult for a maritime radar to achieve high-performance detection of slow and small targets on the sea surface. For such targets, the traditional energy-based statistical detection algorithms suffer from serious performance loss. Confronted with this problem, a detection algorithm of small targets based on Deep Graph Infomax framework is proposed to realize unsupervised target anomaly detection in the background of sea clutter. In the traditional neural networks, there is an assumption that the samples are independent and identically distributed, which, however, the high-resolution radar echo does not meet. Therefore, this paper re-models the data from the perspective of graph and constructs the graph topological structure according to the correlation characteristics of the echo. Moreover, this paper puts forward the relative maximum node degree, and combines it with the relative average amplitude and the relative Doppler vector entropy to be the initial representation vectors of the graph nodes. With the graph modeling done, the graph attention network is used as the encoder in the Deep Graph Infomax framework to learn representation vectors. Finally, the anomaly detection algorithm is used to detect the targets, and the false alarm can be controlled. The detection result on the measured datasets shows that the performance of the proposed detector is improved by 9.2% compared to the three-feature detector when using the fast convex hull learning algorithm. Compared to the time-frequency three-feature detector, the performance is improved by 7.9%. When the network outputs a higher-dimensional representation vectors, the performance of the detector using the isolated forest algorithm is improved by 27.4%.
-
Key words:
- Sea clutter /
- Target detection /
- Graph neural network /
- Unsupervised learning
-
1. 引言
随着无线移动通信的发展，由5G异构蜂窝网络、无线局域网等多种接入技术构成的超密集异构无线网络，可为终端提供多种接入方式，支持终端的无缝移动。超密集组网会带来较高的能耗问题，引入休眠机制会一定程度降低能耗，同时，会进一步增强网络的动态性，导致终端服务质量和网络吞吐量等性能均下降。如何在高动态的超密集异构无线网络，保证终端所获得的吞吐量，并提升网络系统综合切换性能，成为当前研究需要解决的重要课题[1]。
目前，国内外相关研究工作较多，从采取的研究方法来划分，网络选择算法大致可以分成两类：(1)基于参数阈值的网络选择算法[2-5]，主要是以接收信号强度(Receive Signal Strength, RSS)等参数进行网络选择判决。文献[4]基于RSS的阈值，通过比较候选网络的RSS数值大小，从而进行网络选择。该类算法实现简单，选网参数易于获取，计算复杂度较低；但是，该类算法容易导致乒乓效应，无法完全体现接入网络的服务质量。(2)基于模糊逻辑或强化学习等人工智能方法的网络选择算法[6-14]。文献[6]采用模糊逻辑算法，根据终端应用对QoS参数的需求，通过设计不同的隶属度函数，合理地选择网络。该类算法选网效率较高，但是需要事先建立相应的模糊推理规则库，在输入参数增加的情况下，模糊规则库的数量会激增，导致推理时间复杂度过大。文献[8]基于神经网络算法，根据不同业务类型，对分类后的参数进行训练，从而进行网络选择。该类算法具有强大的学习能力，能够根据环境自适应地进行调整。文献[11]提出一种基于体验质量(Quality of Experience, QoE)感知的网络选择方案，将QoS的网络参数映射成QoE参数，然后利用QoE参数构造回报函数，最后采用Q学习算法进行网络选择。该类算法能够通过不断的学习强化已有收益，从而选择高收益网络；但是，如果网络环境过于复杂，会导致网络控制模块学习效果下降，继而导致无法选择到最佳网络。
对于引入休眠机制的超密集异构无线网络环境，随着该网络环境下基站数量的激增，同时引入休眠机制以节能，导致基站数量发生动态改变，继而导致网络动态性增强，网络拓扑结构时变性提高。同时，终端自身的移动性和基站之间由于密集布网所产生的干扰，导致网络动态性进一步加剧，而现有的相关文献，解决的是常规异构无线网络下的网络选择问题，并未考虑到如此高动态的网络环境，这样会使终端在通过现有选网算法切换到目标网络之后，可能因目标网络突然休眠，导致所获得的吞吐量出现快速下滑，无法为终端提供持续稳定的吞吐量，基站之间产生的干扰又会严重影响到终端的服务满意度，最终发生系统切换性能严重降低的问题。因此，上述算法对于这一严峻问题，关注不足。
通过上述对引入休眠机制的超密集异构无线网络环境进行动态性分析，可以得出，该网络环境具有高动态特性，会使现有的网络选择算法出现切换性能严重下降的问题。因此，本文基于一种改进深度Q学习算法，以保证终端所获得的网络吞吐量，缓解系统因高动态性网络环境导致的切换性能严重降低的问题。同时，针对传统的深度Q学习算法在进行网络选择时，由于在线训练神经网络导致时延过大，出现算法失效的情况，本文利用迁移学习，加速训练神经网络，以降低在线选网的时间复杂度。综上，本文的主要贡献可概括为：
(1)针对由无线局域网络和引入休眠机制的超密集蜂窝网络异构而成的超密集异构无线网络环境，进行动态性分析，以期缓解系统切换性能降低的问题。
(2)本文采用迁移学习对深度Q学习算法进行改良，提出一种基于改进深度Q学习的网络选择算法，降低了传统深度Q学习算法在线上选网过程中的时间复杂度。
2. 算法流程
本文算法的流程图如图1所示，主要包括参数采样及初始化过程、深度Q学习选网模型、最优策略及网络选择3个阶段。第1阶段通过周期性采样网络参数的值来初始化深度Q学习选网模型，该模型由线下训练模块与线上决策模块构成，上述两个模块均采用深度Q网络构建；第2阶段利用迁移学习对线下训练模块和线上决策模块进行协同交互；第3阶段通过深度Q学习选网模型得到最优策略并进行网络选择。图1的历史信息数据库包含网络参数的采样值以及历史选网信息数据，作为深度Q学习选网模型的训练数据。
3. 参数采样及初始化过程
3.1 参数采样
由于本文采用深度Q学习算法对网络选择行为进行建模，因此，在通过深度Q学习算法进行建模的过程中，需要周期性采样网络参数的值来构建深度Q学习的动作空间、状态空间和回报函数，以初始化深度Q学习选网模型，本文采样的参数如下。
(1)接收信号强度表示为
RSS=ρij−ηlg(dij)+u1 (1) 其中，
dij 为用户终端i 到网络接入点j 的距离，ρij 为用户终端i 接收到网络接入点j 的发射功率，η 为路径损耗因子，u1 为服从均值为0、标准差为σ1 的高斯白噪声。(2)终端所获下行吞吐量可表示为
C=Wlog2(1+SINR) (2) 其中，
W 为网络的可用带宽，SINR 为用户终端的信干噪比。(3)根据文献[15]建立的干扰模型，干扰影响因子可表示为
ψ=E[exp(I⋅(−β⋅rjαρij))] (3) 其中，
I 为干扰信号强度，β 为用户终端所能接受的最低信干噪比阈值，本文设置为1 dB，rj 为网络接入点j 的半径，α 为路径衰落因子，E(⋅) 为期望函数。(4)根据泊松点过程模型的特征，休眠概率可表示为
P=P(λnow<λmin)=1−λmax∑λmine−λnowλnowλminλmin! (4) 其中，
λnow 为基站当前所接入的终端数，λmin 为基站处于活跃状态的最低接入终端数，λmax 为基站最大可容纳终端数，当λnow<λmin 时，基站进行休眠操作。3.2 初始化过程
本文将超密集异构无线网络环境中终端可以接入的候选网络(基站和访问点)用集合
N={n1,n2,⋯,ni} 表示；其中终端在t 时刻接入候选网络ni 表示为at(ni) ，则本文的动作空间可定义为At={at,at∈{at(n1),at(n2),⋯,at(ni)}} 。本文将状态空间定义为
St=(rsst,ct,ψt,pt) ，其中，rsst 表示在t 时刻各候选网络的接收信号强度集合，ct 表示在t 时刻各候选网络的吞吐量集合，ψt 表示在t 时刻各候选网络的干扰影响因子集合，pt 表示在t 时刻各候选网络的休眠概率集合。本文为最大化终端所获得的吞吐量，通过考虑网络的吞吐量、干扰影响因子和休眠概率，结合文献[16]中回报函数的构造方式，将回报函数定义为
R(St,at)={1−e−Ct(ni)Pt(ni)ψt(ni),at=at(ni)−1,其他 (5) 其中，
Ct(ni) 表示在t 时刻终端接入候选网络ni 获得的吞吐量，ψt(ni) 表示在t 时刻终端接入候选网络ni 后受到的干扰影响因子，Pt(ni) 表示在t 时刻候选网络ni 的休眠概率。4. 深度Q学习选网模型
4.1 改进深度Q学习算法
本文将引入休眠机制的超密集异构无线网络环境下的选网问题，基于深度Q学习算法进行建模求解，该算法过程利用Q函数实现。Q函数表示在状态
S 下执行动作a ，以及采取后续动作所产生累计回报值的期望，定义为Q(S,a)=∞∑t=0γtE(R(St,at)) (6) 其中，
γt∈[0,1] 为折扣因子，用于调整对未来回报的重视程度，随着时刻t 的增加而呈现指数型下降趋势，E(⋅) 为期望函数。由式(6)可得，
Q(S,a) 在t→+∞ 时才能收敛到最佳Q值，在实际的网络选择过程中很难实现。因此，深度Q学习算法利用神经网络构建Q(S,a;θ) ，其中，θ 为权值，使得Q(S,a;θ)≈max(Q(S,a)) 来进行近似求解。对于传统的深度Q学习算法，终端需要多次进行交互以获取足够样本，但是，这样会使神经网络的训练时间过长，导致算法因延迟过高而失效。综上，本文引入迁移学习[17]，提出一种改进深度Q学习算法，来解决上述问题，该算法能够减少终端与网络环境实时交互的次数。同时，相比传统深度Q学习算法以随机赋权值的方法来训练神经网络，迁移线下训练权值之后，使得训练的起点更加接近神经网络收敛条件，从而加速了算法的收敛性。
4.2 线上线下协同模块
4.2.1 样本与权重的生成及迁移
本文所提的深度Q学习选网模型由线下训练模块与线上决策模块构成，而上述两个模块均由深度Q网络构建。为了加速线上决策模块的神经网络训练过程，通过迁移线下训练模块的训练样本与权值，并对迁移后上述两个模块产生的训练误差进行校正，直到误差恒定，整个迁移学习过程结束。其中，训练样本与权值的生成及迁移过程如下：
神经网络的训练样本是由历史信息数据库中不同时刻的当前状态、动作、回报值以及未来状态所构成的，即
(St,at,Rt,St+1) ，其中，t∈(0,+∞) 。在深度Q网络中，为了高效地训练神经网络，通过设置经验回放池，以缓解训练过程中出现的迭代不稳定问题。因此，本文将线下训练模块的训练样本迁移到线上决策模块中，利用迁移的线下训练样本以及线上学习样本，构建线上决策模块的经验回放池，表示为Dsum=Don+ξtDoff (7) 其中，
Dsum 为经验回放池存放的样本总量，Don 为线上学习样本的总量，初始值为0，Doff 为线下训练样本的总量，ξt 为样本迁移率，ξ∈[0,1] 为迁移率因子，ξt 随着时刻t 的增加呈现指数型下降的趋势，即有t→∞ ，ξt→0 。在线上决策模块的经验回放池构建完成后，将线下训练得到的神经网络权值
θoff 迁移到线上决策模块中，作为神经网络训练的初始权值，即θon=θoff 。4.2.2 迁移误差调整
在神经网络进行迭代训练时，由于线下训练模块与线上决策模块之间在训练样本、权值存在差异的情况，可能出现训练样本、权值迁移过后，线上决策模块的神经网络训练效果不佳，从而导致神经网络的收敛速度未能达到预期效果。为了解决上述问题，本文将线下训练与线上决策模块之间产生的训练误差定义为策略损失，为了将策略损失降至最低，采用策略模仿机制，通过线下训练模块中，预估Q值
Qoff(St,at;θoff) 的玻尔兹曼分布，将线下训练模块的估值网络转化为线下策略网络πoff(St,at;θoff) ，表示为πoff(St,at;θoff)=e1TQoff(St,at;θoff)∑at+1∈Aoffe1TQoff(St,at+1;θoff) (8) 其中，
T 为服从玻尔兹曼分布的参数，Aoff 为线下训练时的动作空间。同样，利用线上决策模块的预估Q值Qon(St,at;θon) ，将估值网络转化为线上策略网络πon(St,at;θon) ，表示为πon(St,at;θon)=e1TQon(St,at;θon)∑at+1∈Aone1TQon(St,at+1;θon) (9) 线下训练与线上决策模块之间的策略损失采用交叉熵衡量，则策略模仿损失函数表示为
F(θoff)=∑at∈Aoffπoff(St,at;θoff)∑at∈Aonlgπon(St,at;θon) (10) 在策略损失存在的情况下，线上决策模块预估Q值
Qon(St,at;θon) 的梯度更新表示为ΔF(θoff)=[Qπ(St,at;θon)−Qon(St,at;θon)]⋅∂Qon(St,at;θon)∂F(θoff) (11) 其中，
Qπ(St,at;θon) 表示在策略π 下预估Q值的无偏差估计值。当
ΔF(θoff)=0 时，线下训练与线上决策模块之间的策略损失不再改变，即基于策略模仿机制的训练迭代过程实现收敛，则Qπ(St,at;θon)≈Qon(St,at;θon) ，此时迁移学习过程结束。5. 最优策略及网络选择
终端在移动过程中，当其将要进入或者离开某个基站时，会出现网络选择决策时刻，此时终端需要进行网络选择，本文为了得到终端所要面临的网络选择决策时刻，根据网络的接收信号强度与终端的移动速度来进行预测，假设终端在基站覆盖范围内的移动模型如图2所示，O点表示基站所在的位置，M点为弦AC的中点，A点表示终端在网络选择决策时刻
tA 所处的位置，B点表示终端自A点移动Δl 后所处的位置，根据终端当前的运动趋势，预测在C点处将出现网络选择决策时刻tC ，由图2中△OAM 和△OBM 的关系可以得到r2=l2OM+(Δl+lBM)2l2OB=l2OM+l2BM} (12) 其中，
lBM=r2−l2OB−(Δl)22Δl (13) 通过检测B点接收信号强度值，可得到基站到B点的距离
lOB ，终端在基站覆盖范围内的平均移动速度可表示为¯V ，则网络选择决策时刻tC 表示为tC=tA+2(Δl+lBM)¯V (14) 假设在网络决策时刻
t ，候选网络中最大Q值对应的网络为nm ，则终端在决策时刻t 的最佳选网动作为at(nm) ，以此类推，终端在不同网络决策时刻所构成的最佳选网动作集合，定义为最优策略π∗ ，该策略表示终端与候选网络在不同的网络决策时刻实现最佳匹配。6. 仿真结果与分析
6.1 系统模型和仿真参数设置
本文采用5G异构蜂窝网络和无线局域网(Wireless Local Area Network, WLAN)组成超密集异构无线网络环境，无线接入网络均采用正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术。仿真场景如图3所示，并在MATLAB平台进行仿真。仿真场景中，有2个5G宏基站、4个5G微基站和3个WLAN接入点，5G宏基站的半径均为800 m，5G微基站的半径均为300 m，WLAN的半径均为80 m。假设用户随机分布在仿真区域内，每隔一段时间随机改变运动方向。仿真过程中，假设终端在网络选择决策时刻
k 获得的候选网络参数如表1所示。表 1 候选网络的参数值网络 接收信号强度(dBm) 路径损失(dB) 噪声偏差(dBm) 吞吐量(kbps) 负载量(个) MBS1 –85 48 6 1100 68 MBS2 –70 51 9 900 52 SBS1 –78 47 8 2700 16 SBS2 –72 53 8 2600 23 SBS3 –86 50 7 2900 25 SBS4 –95 49 6 3100 20 AP1 –60 45 9 4800 12 AP2 –75 43 6 6400 8 AP3 –71 47 7 5500 10 仿真对比了本文算法与现有基于Q学习(Q-learning)的网络选择算法[11]、基于深度Q学习网络(Deep Q-Network, DQN)的网络选择算法[12]以及基于长短期记忆神经网络(Long Short-Term Memory, LSTM)的网络选择算法[13]。
6.2 时间复杂度分析
时间复杂度是网络选择算法的一个重要指标，本文算法与另外3种算法的时间开销对比如图4所示，随着迭代次数的增加，4种算法所消耗的时间都在增加；但是，本文所采用的算法时间增加的幅度明显慢于另外3种算法。这是因为本文算法采用迁移学习对传统深度Q学习算法进行改进，极大地减少了神经网络训练时间，从而使整个算法的时间消耗降低。对于Q学习算法，在状态与动作空间迅速增大的时候，计算能力持续下降，耗时逐渐加大，与本文算法的时间差距逐渐拉开。而DQN算法和LSTM算法，则直接采用深度神经网络进行迭代运算，在迭代次数巨大的情况下，它们与本文算法的时间消耗差距将更为显著。
6.3 信干噪比分析
图5给出了随着仿真次数的增加，终端在4种算法下受到的平均信干噪比数值情况。通过对比可以看到，采用本文算法所得到的平均信干噪比，高于另外3种算法。这是因为本文考虑到终端所受到的干扰，将干扰因素考虑进来，成功预测了基站未来对终端所造成的干扰影响情况，最大限度地降低了因基站所产生的干扰而对终端造成损失；同时，通过引用干扰影响因子参数来构建深度Q学习算法的回报函数，有效缓解了干扰对终端产生的影响，从而为用户带来更高的信干噪比。对于其他3种算法，由于没有专门考虑终端受到干扰的情况，为用户设计合适的回报函数来降低干扰影响，导致了平均信干噪比没有本文算法高。
6.4 网络吞吐量分析
图6给出了随着仿真次数的增加，终端在4种算法下平均吞吐量变化情况。通过对比可以得出，采用本文算法所得到的平均吞吐量，远高于另外3种算法。这是因为本文采用深度Q学习算法成功预测了基站未来因休眠机制所导致的状态变化情况，使得终端可以根据网络未来发生的动态性变化合理地选择网络，极大地降低了由于基站干扰和休眠情况造成的吞吐量损失；同时，本文根据用户获得的吞吐量定义深度Q学习算法的回报函数，更加符合用户的实际需求。对于3种算法，由于它们既没有充分考虑在未来网络环境下基站的状态，也没有为用户设计合适的回报函数来增加网络吞吐量，从而导致了吞吐量没有本文算法高。
6.5 掉话率分析
图7为4种算法的掉话率与用户数之间的比较。由图可以看出，虽然4种算法的掉话率都在缓慢增加，但是，在用户数增加到40以后，本文算法的掉话率增加幅度最小，另外3种算法增加幅度明显高于本文算法。这是因为本文算法相比较其他3种算法，在网络动态性持续增加的情况下，能够预测到未来网络的变化情况，继而为用户提供较高质量的网络进行选择，有效地降低了切换失败的可能性。对于Q学习算法，由于不能够准确地对网络状态进行预测，在用户数增加的情况下，掉话率急剧增加。同样，对于DQN和LSTM算法，由于在训练深度神经网络的过程中，会造成选网时延较高的结果，使得掉话率上升明显。
6.6 乒乓效应分析
图8为用户采用4种算法后产生的总切换次数。由图可以看出，在用户数不断增加的情况下，采用本文算法产生的网络总切换次数，在所述4种算法中始终处于最低。这是因为本文考虑了因网络环境动态性增强，导致算法切换失效率增加，从而发生频繁切换的情况。本文算法成功预测了用户在进行网络选择之后的网络状态变化情况，从而使发生切换的次数大大降低。而另外3种算法，由于均未妥善解决基站因休眠机制带来的网络高动态性影响，导致网络的切换频发，乒乓效应加剧；因此，本文算法能够有效地降低无谓的网络切换。
7. 结束语
本文提出一种基于改进深度Q学习的网络选择算法，缓解了在引入休眠机制的超密集异构无线网络中，由于网络动态性的明显提升而引发系统切换性能降低的问题。通过利用网络参数来构建回报函数，从而尽可能地降低引入休眠机制后，网络高动态性所造成的影响；同时，通过迁移学习对传统的深度Q学习算法进行优化，使得算法的时间复杂度大大降低。实验结果表明，该算法在提升网络吞吐量的同时，降低了时间复杂度，减少了网络切换次数。
-
表 1 快速凸包算法在IPIX数据集20组数据不同极化情况下平均检测概率
检测器 HH HV VH VV 平均 三特征检测器 0.6544 0.7825 0.8222 0.6343 0.7234 时频三特征检测器 0.6961 0.7911 0.8173 0.6426 0.7368 本文所提检测器 0.7800 0.8505 0.8749 0.7574 0.8157 
下载: 导出CSV
表 2 孤立森林算法在IPIX数据集20组数据不同极化情况下平均检测概率
检测器 HH HV VH VV 平均 8特征孤立森林检测器 0.3269 0.5085 0.5623 0.2998 0.4244 本文所提检测器 0.5965 0.8001 0.8252 0.5716 0.6983
下载: 导出CSV
-
[1] 许述文, 白晓惠, 郭子薰, 等. 海杂波背景下雷达目标特征检测方法的现状与展望[J]. 雷达学报, 2020, 9(4): 684–714. doi: 10.12000/JR20084.XU Shuwen, BAI Xiaohui, GUO Zixun, et al. Status and prospects of feature-based detection methods for floating targets on the sea surface[J]. Journal of Radars, 2020, 9(4): 684–714. doi: 10.12000/JR20084. [2] HU Jing, TUNG W W, and GAO Jianbo. Detection of low observable targets within sea clutter by structure function based multifractal analysis[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(1): 136–143. doi: 10.1109/TAP.2005.861541. [3] SHI Sainan and SHUI Penglang. Sea-surface floating small target detection by one-class classifier in time-frequency feature space[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(11): 6395–6411. doi: 10.1109/TGRS.2018.2838260. [4] SHUI Penglang, LI Dongchen, and XU Shuwen. Tri-feature-based detection of floating small targets in sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1416–1430. doi: 10.1109/taes.2014.120657. [5] LI Yuzhou, XIE Pengcheng, TANG Zeshen, et al. SVM-based sea-surface small target detection: A false-alarm-rate-controllable approach[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(8): 1225–1229. doi: 10.1109/LGRS.2019.2894385. [6] 郭子薰, 水鹏朗, 白晓惠, 等. 海杂波中基于可控虚警K近邻的海面小目标检测[J]. 雷达学报, 2020, 9(4): 654–663. doi: 10.12000/JR20055.GUO Zixun, SHUI Penglang, BAI Xiaohui, et al. Sea-Surface small target detection based on K-NN with controlled false alarm rate in sea clutter[J]. Journal of Radars, 2020, 9(4): 654–663. doi: 10.12000/JR20055. [7] 苏宁远, 陈小龙, 陈宝欣, 等. 雷达海上目标双通道卷积神经网络特征融合智能检测方法[J]. 现代雷达, 2019, 41(10): 47–52,57. doi: 10.16592/j.cnki.1004-7859.2019.10.009.SU Ningyuan, CHEN Xiaolong, CHEN Baoxin, et al. Dual-channel convolutional neural networks feature fusion method for radar maritime target intelligent detection[J]. Modern Radar, 2019, 41(10): 47–52,57. doi: 10.16592/j.cnki.1004-7859.2019.10.009. [8] WAN Hao, TIAN Xiaoqing, LIANG Jing, et al. Sequence-feature detection of small targets in sea clutter based on Bi-LSTM[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 4208811. doi: 10.1109/TGRS.2022.3198124. [9] YAN Kun, BAI Yu, WU H C, et al. Robust target detection within sea clutter based on graphs[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(9): 7093–7103. doi: 10.1109/TGRS.2019.2911451. [10] 时艳玲, 姚婷婷, 郭亚星. 基于图连通密度的海面漂浮小目标检测[J]. 电子与信息学报, 2021, 43(11): 3185–3192. doi: 10.11999/JEIT201028.SHI Yanling, YAO Tingting, and GUO Yaxing. Floating small target detection based on graph connected density in sea surface[J]. Journal of Electronics & Information Technology, 2021, 43(11): 3185–3192. doi: 10.11999/JEIT201028. [11] 许述文, 焦银萍, 白晓惠, 等. 基于频域多通道图特征感知的海面小目标检测[J]. 电子与信息学报, 2023, 45(5): 1567–1574. doi: 10.11999/JEIT220188.XU Shuwen, JIAO Yinping, BAI Xiaohui, et al. Small target detection based on frequency domain multichannel graph feature perception on sea surface[J]. Journal of Electronics & Information Technology, 2023, 45(5): 1567–1574. doi: 10.11999/JEIT220188. [12] SU Ningyuan, CHEN Xiaolong, GUAN Jian, et al. Maritime target detection based on radar graph data and graph convolutional network[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4019705. doi: 10.1109/lgrs.2021.3133473. [13] CHEN Simin, FENG Chen, HUANG Yong, et al. Small target detection in x-band sea clutter using the visibility graph[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5115011. doi: 10.1109/TGRS.2022.3186283. [14] VELIČKOVIĆ P, FEDUS W, HAMILTON W L, et al. Deep graph infomax[J]. arXiv: 1809.10341, 2018. doi: 10.48550/arXiv.1809.10341. [15] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks[C]. Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 2018. [16] LACASA L, LUQUE B, BALLESTEROS F, et al. From time series to complex networks: The visibility graph[J]. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(13): 4972–4975. doi: 10.1073/pnas.07092471. [17] BRUNA J, ZAREMBA W, SZLAM A, et al. Spectral networks and locally connected networks on graphs[J]. arXiv: 1312.6203, 2013. doi: 10.48550/arXiv.1312.6203. [18] DEFFERRARD M, BRESSON X, and VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering[C]. Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 2016. [19] KIPF T N and WELLING M. Semi-supervised classification with graph convolutional networks[C]. Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 2017. [20] LIU F T, TING Kaiming, and ZHOU Zhihua. Isolation forest[C]. Proceedings of the 8th IEEE International Conference on Data Mining, Pisa, Italy, 2008: 413–422. doi: 10.1109/ICDM.2008.17. [21] XU Shuwen, ZHU Jianan, JING Junzheng, et al. Sea-surface floating small target detection by multifeature detector based on isolation forest[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 704–715. doi: 10.1109/JSTARS.2020.3033063. [22] ECHARD J D. Estimation of radar detection and false alarm probability[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(2): 255–260. doi: 10.1109/7.78300. -
下载:
计量
- 文章访问数: 346
- HTML全文浏览量: 181
- PDF下载量: 70
- 被引次数: 0
下载:
