1.   引言

电磁环境频谱地图(Spectrum Map)也称为频谱态势图或者无线环境地图，能够从时间、空间、频率和能量等多个维度对电磁环境的当前状态和未来发展趋势进行定量描述，并结合地理信息系统(Geographic Information System, GIS)进行可视化呈现。频谱地图在干扰协调、无线网络规划、动态频谱共享以及频谱管控等方面具有广泛应用，能够有效缓解频谱冲突、降低无线通信系统开销，提高电磁频谱管理效率和智能化水平^[1]。频谱地图是由辐射源和地理环境共同作用的结果，可建模为地理空间位置、时间和频率的复杂函数。受限于传感器数量、数据计算、存储和通信资源的约束，很难对每个地理空间位置部署传感器采集样本数据，而利用少量传感器获取局部监测样本数据以构建出全局频谱地图的算法成为该领域研究的重点。

目前已经提出了大量的频谱地图构建算法。Atanasovski等人^[2]提出了一种频谱地图的原型，旨在存储和估计从传感器获得的频谱数据，这为频谱地图构建提供了指导性工作。Romero 等人^[3]使用在线随机梯度下降法来重建功率谱密度图，该算法需要辐射源位置作为先验信息。文献[4]提出了一种基于自适应高斯径向基函数的频谱地图构建框架，不需要辐射源的先验信息，能够非参数地构建频谱地图。此外，克里金法^[5]、字典学习^[6]、稀疏贝叶斯学习^[7]、矩阵补全^[8]等算法也被用于频谱地图构建。上述算法都是基于插值或者模拟无线电传播现象的模型驱动算法，算法的性能高度依赖于模型的准确性。然而，实际的无线电传播环境是动态复杂的，不适合的模型会严重影响频谱地图的构建精度。为了解决这一问题，提出了数据驱动算法，利用深度神经网络(Deep Neural Network, DNN)从历史数据集中学习潜在的电磁波传播现象，如自由空间损耗、阴影、反射和衍射等。在此基础上，Krijestorac等人^[9]提出了一种基于生成对抗网络的功率谱图估计算法，并建立了回归图像重建模型。Teganya等人^[10]设计了一种深度补全自编码器，从电磁环境中预先学习传播现象，仅需要少量的样本数据即可重建高精度的频谱地图。在上述研究中，传感器监测的位置是固定的或者随机的，没有考虑对监测位置的优化以捕捉不同空间位置相关性。对此，Shen等人^[11]提出了基于QR旋转的观测位置优化算法，但是该算法需要地理环境的先验信息来建立准确的电磁波传播模型。文献[12]提出了空间相关性不确定度的概念，认为不确定度越高的区域频谱信息越丰富，并提出了一种基于动态规划的传感器采样路径算法，以构建精确的频谱地图。此外还有一些特定场景下的算法，文献[13]研究了不可达区域的远程频谱地图构建问题，利用可达区域中的少量采样数据来预测不可达区域的频谱地图，并提出了一种基于交替方向乘子法来估计不可达区域的功率大小。

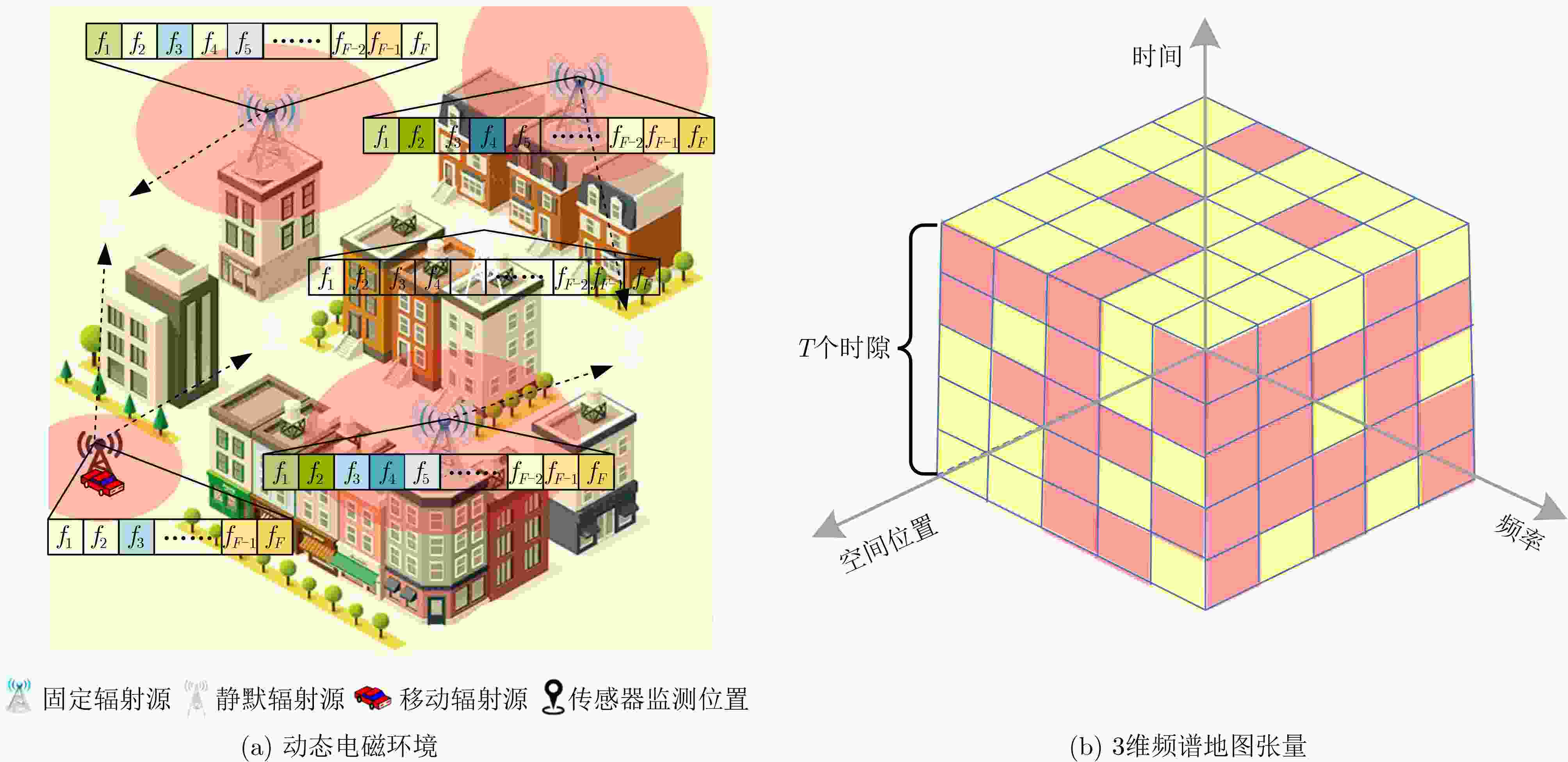
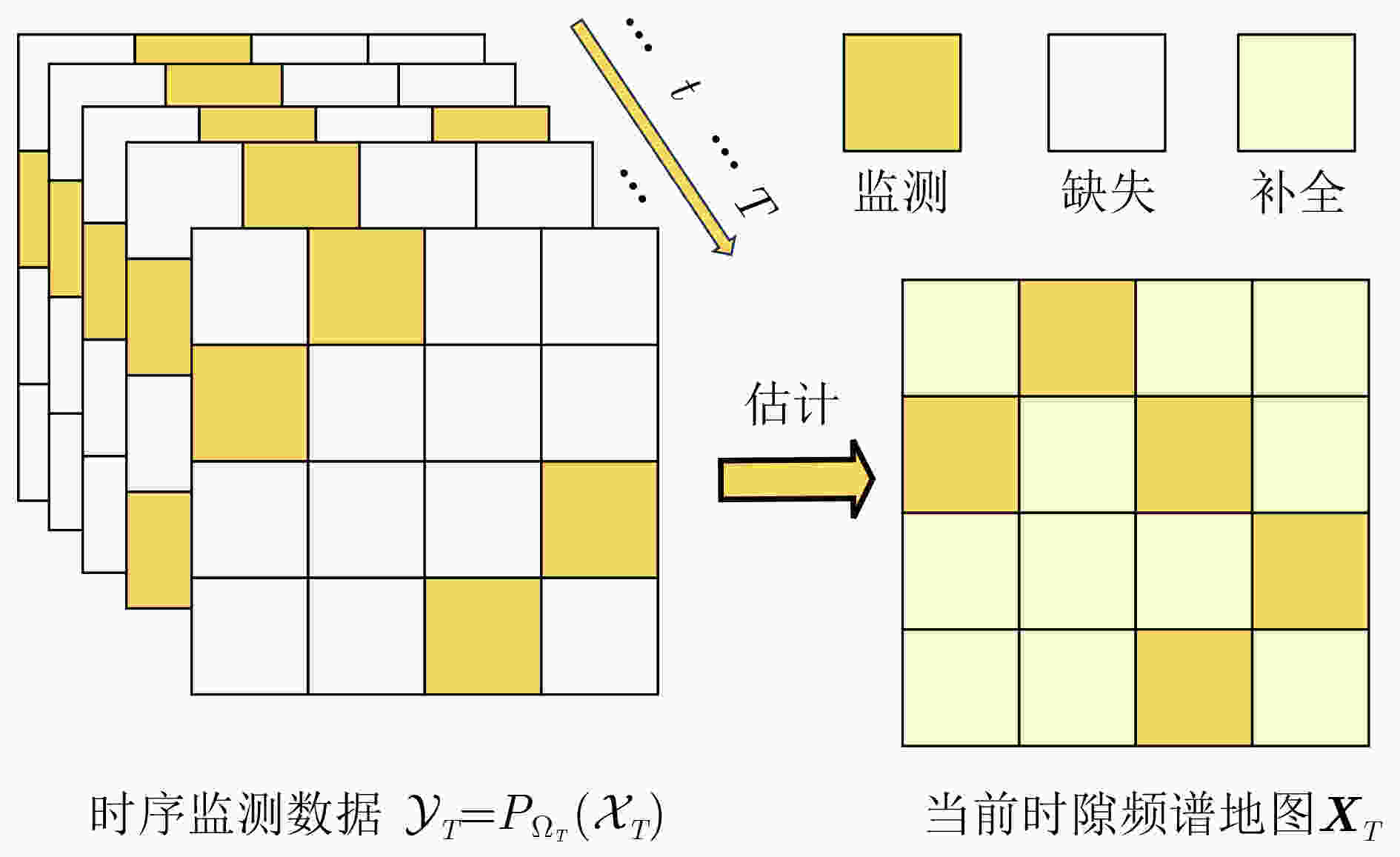
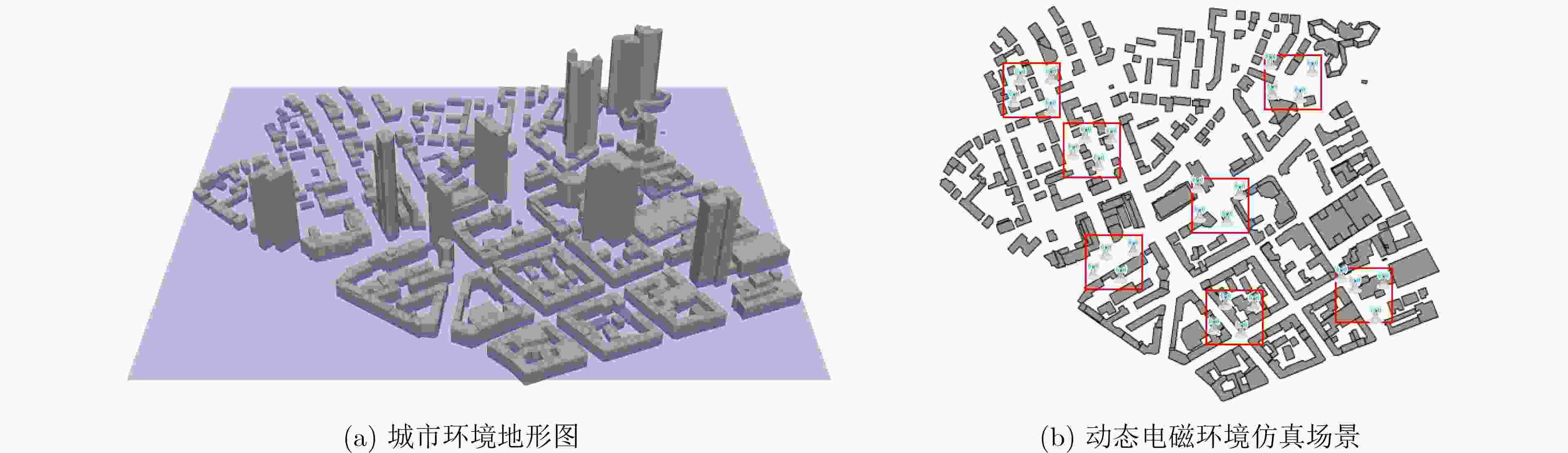
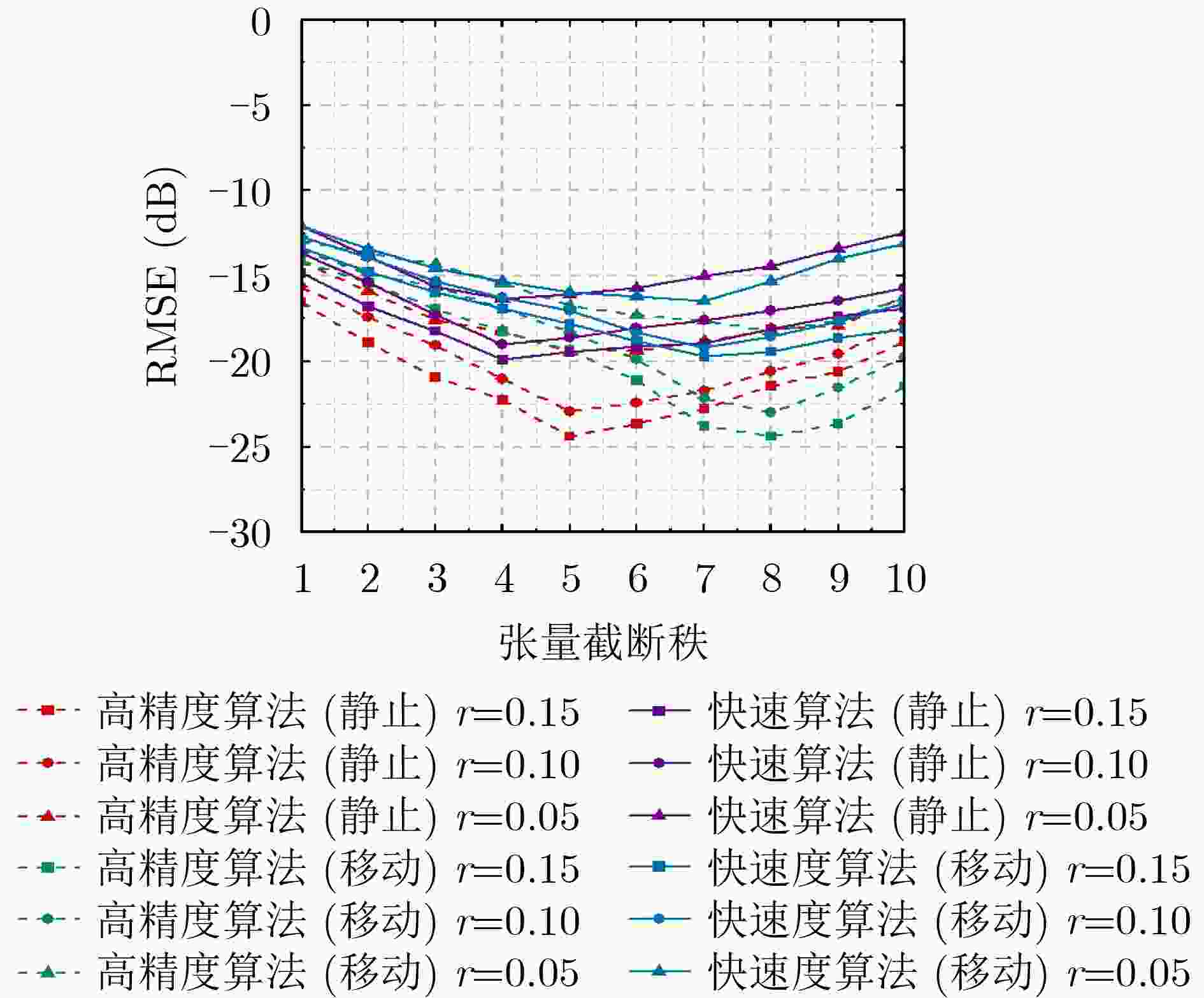
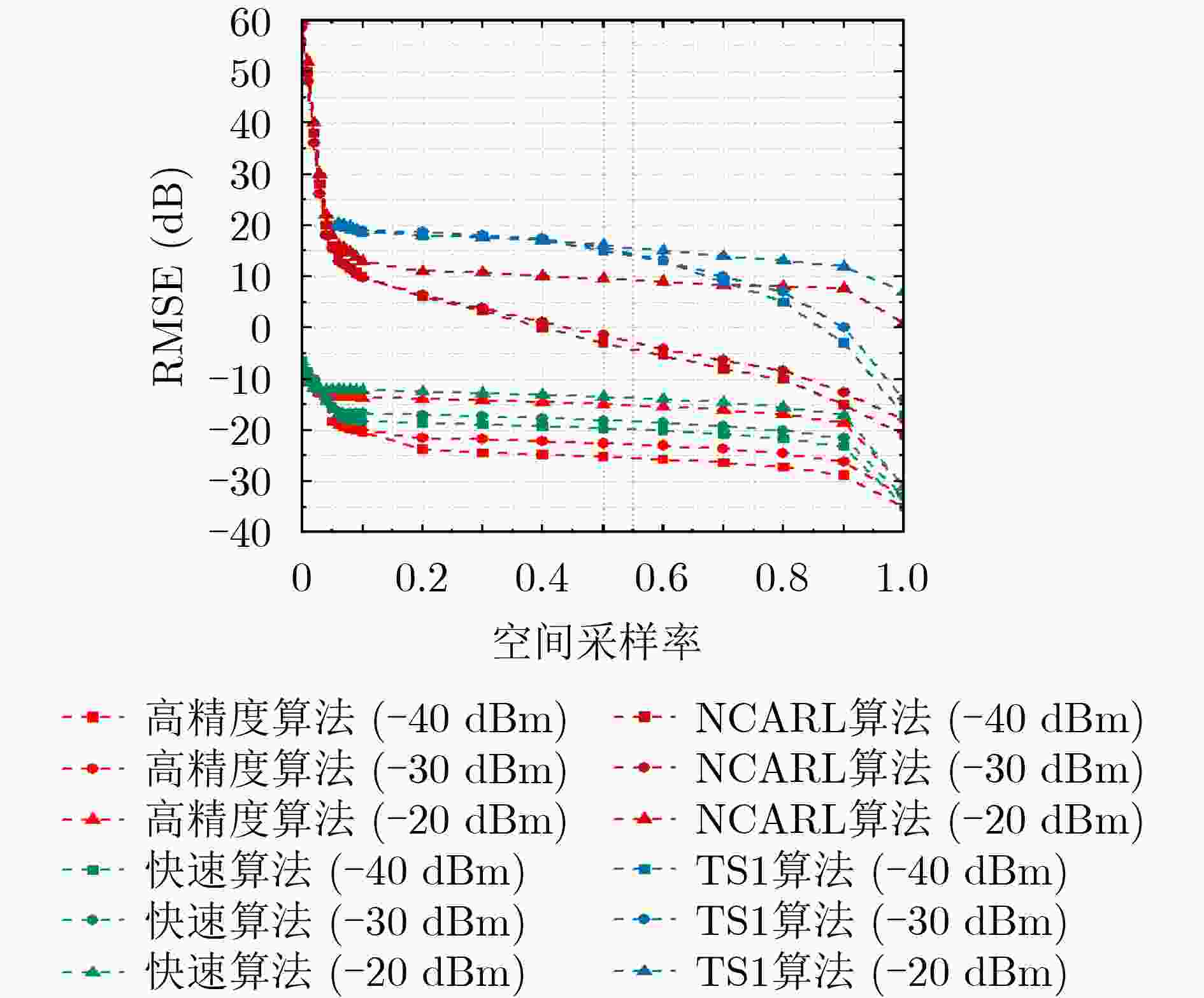
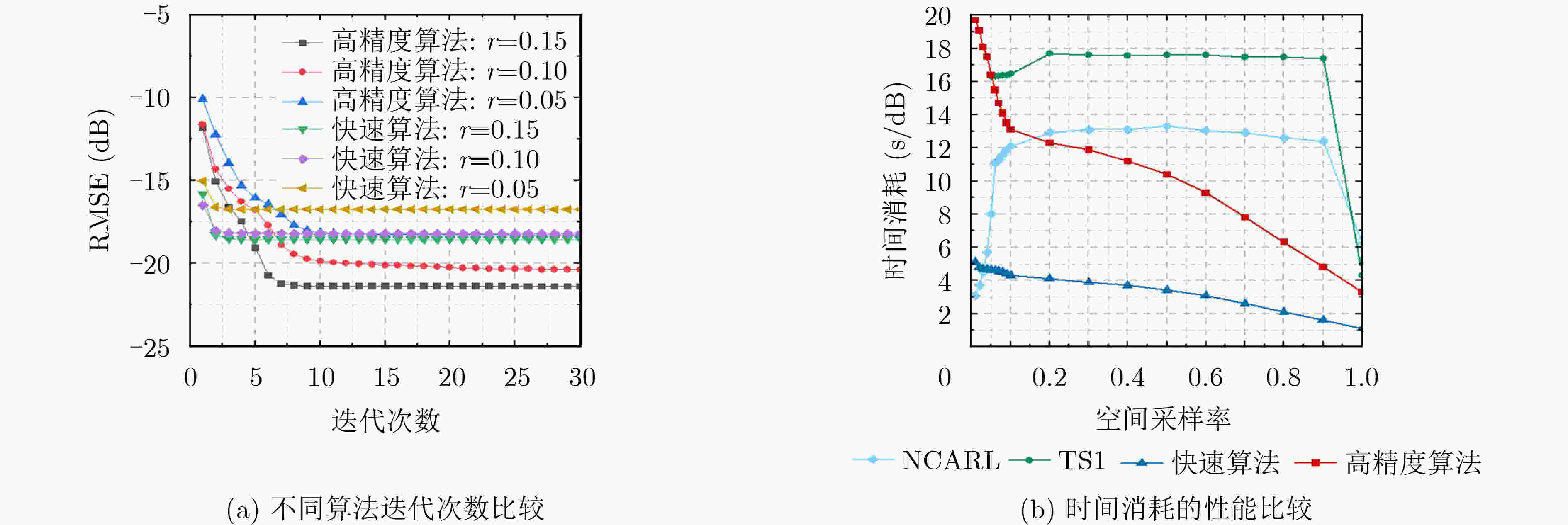
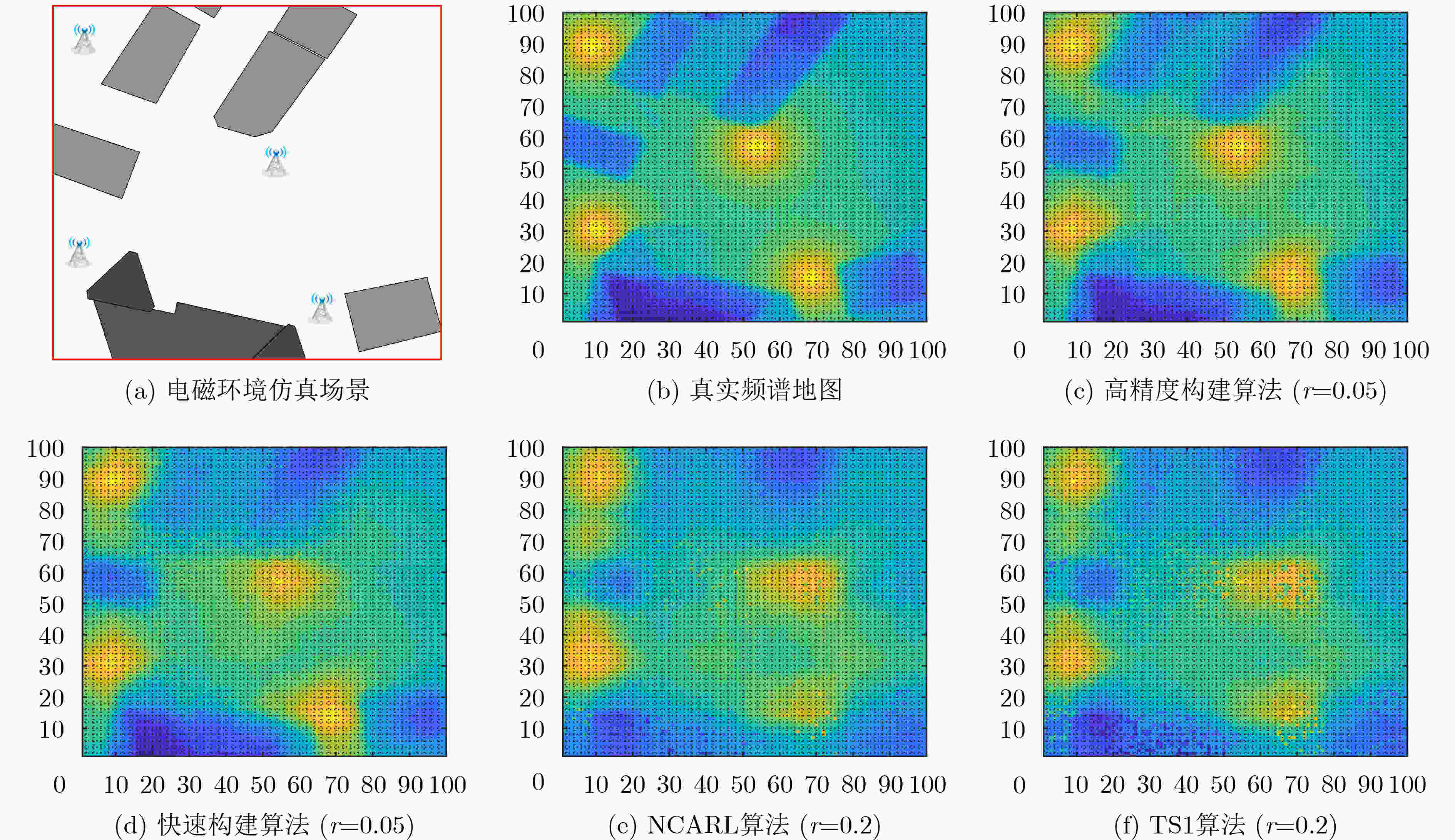
本文研究使用少量监测样本数据构建动态电磁环境的时变频谱地图。首先采用张量表征方法将动态电磁环境的时变频谱地图建模为3维频谱张量。根据时间、空间、频率对辐射源信号传播的影响，对3维频谱张量进行Tucker分解，提取出具有物理意义的核张量和因子矩阵等低维特征，这是首次将张量Tucker分解模型应用到时序频谱地图构建。根据频谱张量时域、空域、频域之间的相关性以及监测样本数据的稀疏性，设计一种基于Tucker分解的低秩张量补全模型，将频谱地图构建任务转化为数据缺失的低秩张量补全优化问题。相比于矩阵表征法，张量表征法能够有效保持多维数据空间结构信息，在较弱的约束条件下具有本征唯一性，能够唯一地求解出具有物理意义的低维特征成分。本文提出了两种无需先验信息的频谱地图构建算法：高精度频谱地图构建算法和快速频谱地图构建算法。前者采用交替最小二乘法(Alternating Least Squares, ALS)求解数据缺失的低秩张量补全问题，对核张量和因子矩阵交替求解，通过“补全-分解”的迭代过程实现对频谱地图的高精度构建。后者采用序列截断高阶奇异值分解法(Sequential Truncated High Order Singular Value Decomposition, ST-HOSVD)，对潜在多个低秩近似张量加权平均，该算法具有收敛快速和计算复杂度低的优势，在牺牲少量构建精度的情况下能够快速构建频谱地图。本文采用真实的城市地理数据进行广泛的仿真研究。仿真结果显示，与传统的基准频谱地图构建算法相比，我们提出的两种频谱地图构建算法在所需样本数量方面表现更出色，并且能够实现更高的构建精度和噪声鲁棒性。

2.   符号和相关定义

本文通篇使用了以下符号，小写字母 $\left( {a,b,\cdots } \right)$表示标量，小写粗体字母 $\left( {{\boldsymbol{a}},{\boldsymbol{b}},\cdots } \right)$表示向量，大写粗体字母 $\left( {{\boldsymbol{A}},{\boldsymbol{B}},\cdots } \right)$表示矩阵，大写花体字母 $\left( {\mathcal{A},\mathcal{B},\cdots } \right)$表示张量。 $N$阶张量 $\mathcal{X} \in {\mathbb{R}^{{I_1} \times {I_2} \times \cdots \times {I_N}}}$，其元素表示为 $x_{{i_1},{i_2},\cdots ,{{i_N}}},{i_n} \in \left\{ {1,2,\cdots ,{I_n}} \right\},n \in \left\{ {1,2,\cdots ,N} \right\}$。张量可以用一组2维切片的矩阵表示，3阶张量 $\mathcal{X} \in {\mathbb{R}^{{I_1} \times {I_2} \times {I_3}}}$的切片分别表示为 ${\mathcal{X}_{{i_1},:,:}},{\mathcal{X}_{:,{i_2},:}}, {\mathcal{X}_{:,:,{i_3}}}$。模 $n$展开是将张量 $\mathcal{X} \in {\mathbb{R}^{{I_1} \times {I_2} \times \cdots \times {I_N}}}$沿着第 $n$维展开为一个矩阵 ${{\boldsymbol{X}}_{\left( n \right)}} \in {\mathbb{R}^{{I_n} \times \prod\nolimits_{k \ne n} {{I_k}} }}$。张量中的任一元素可以在展开矩阵 ${{\boldsymbol{X}}_{\left( n \right)}}$的位置 $\left( {{i_n},{i_c}} \right)$上找到，其中 ${i_c} = 1 + \displaystyle\sum\nolimits_{m = 1,m \ne n}^N {\left[ {\left( {{i_m} - 1} \right)\prod\nolimits_{l = 1,l \ne n}^{m - 1} {{I_l}} } \right]}$。定义 ${\left\| \mathcal{X} \right\|_{\mathrm{F}}} = {\left( {{{\displaystyle\sum\nolimits_{{i_1},{i_2},\cdots ,{i_N}} {\left| {{x_{{{{{i_1},}}{{i_2},\cdots ,}}{{i_N}}}}} \right|} }^2}} \right)^{\tfrac{1}{2}}}$为张量的Frobenius范数。对于任意的 $1 \le k \le N$阶张量，有 ${\left\| \mathcal{X} \right\|_{\text{F}}} = {\left\| {{{\boldsymbol{X}}_{\left( k \right)}}} \right\|_{\text{F}}}$， $1 \le k \le N$。非负的上标符号表示迭代索引， ${\mathcal{X}^k}$表示张量 $\mathcal{X}$的第 $k$次迭代。本文还使用了以下矩阵计算符号，其中 $\left\langle {{\boldsymbol{X,Y}}} \right\rangle$表示矩阵的内积， ${\boldsymbol{X}} \otimes {\boldsymbol{Y}}$表示矩阵的Kronecker积。

3.   系统模型和问题表述

3.1   系统模型

考虑如图1(a)所示的电磁环境，固定辐射源和移动辐射源工作在 $F$个频段上，形成了动态时变的电磁频谱环境，红色区域表示频谱能量高，黄色区域表示频谱能量低，环境中随机部署传感器接收辐射源的信号。将2维平面地理空间划分为一组 $L = n \times n$的正方形小网格，网格内一个时隙的平均接收信号强度作为频谱数据， $T$个时隙的历史频谱数据可以建模为如图1(b)的3维频谱地图张量 ${\mathcal{X}_T} \in {\mathbb{R}^{L \times F \times T}}$, $x$轴、 $y$轴、 $z$轴分别是空间位置、频率和时间的索引，张量的元素 ${x_{l,f,t}},l \in \left\{ {1,2,\cdots ,L} \right\}, f \in \left\{ {1,2,\cdots ,F} \right\},t \in \left\{ {1,2,\cdots ,T} \right\}$表示在第 $f$个频段、第 $l$个网格位置、第 $t$个时隙的信号强度。为了对频谱地图张量已知的元素和未知的元素进行建模，构建索引集合 ${\Omega _T}$和采样函数 ${P_{{\Omega _T}}}\left( \cdot \right)$，则监测样本数据 ${\mathcal{Y}_{\text{T}}}$表示为

图 1  动态电磁环境时变频谱地图建模

下载: 全尺寸图片 幻灯片

将每个时隙的监测样本数据按照时间顺序堆叠，形成监测样本张量，如图2所示。频谱地图构建任务是根据时序监测样本数据 ${\mathcal{Y}_T}$，构建出当前时隙的频谱地图 ${{\boldsymbol{X}}_T} = {\mathcal{X}_{:,:,T}}$。

图 2  频谱地图构建任务

下载: 全尺寸图片 幻灯片

3.2   问题表述

频谱地图构建的任务是基于时序监测样本张量 ${\mathcal{Y}_T}$，对当前 $T$时隙的频谱地图 ${{\boldsymbol{X}}_T}$进行估计补全，该问题属于张量补全的范畴。待补全张量具有低秩特征是使用张量补全的先决条件，即张量数据具有高相关性。文献[14]利用实地测量的频谱数据证明了3阶频谱张量的时间、空间地理位置、频率之间具有高相关性和良好的低秩结构。因此，频谱地图重建任务可以视为数据缺失张量的低秩近似补全，并建模为如下的优化问题

其中， $\mathcal{X}$是待补全张量， $\mathcal{Y}$是监测样本张量， ${\rm{rank}}\left( \cdot \right)$表示张量的秩。式(2)假定待补全张量具有低秩结构，对张量秩进行最小化优化，从而补全张量。但张量秩的优化是NP-hard问题，为使式(2)的优化问题可解，本文采用Tucker分解实现张量低秩补全。对张量 $\mathcal{X}$进行Tucker分解可得

其中， $\left( {{R_1},{R_2},{R_3}} \right)$是张量 $\mathcal{X}$的Tucker秩， ${\boldsymbol{S}},{\boldsymbol{U}},{\boldsymbol{V}}$表示因子矩阵， $\mathcal{G}$表示核张量。可以将Tucker分解简写为 $\mathcal{X}=\left[\kern-0.15em\left[ \left. {\mathcal{G};{\boldsymbol{S}},{\boldsymbol{U}},{\boldsymbol{V}}} \right]\kern-0.15em\right] \right.$。对于张量 $\mathcal{X}$中的元素有如下计算公式

根据式(4)，将张量Tucker分解模型应用到时序频谱地图构建中，对3维频谱张量的Tucker分解所得到的低维特征信息赋予物理含义。当因子矩阵单位正交时，Tucker分解具有本征唯一性。核张量以及因子矩阵的物理意义能够为频谱地图的参数估计和信息挖掘等应用提供理论依据。3维频谱张量每个元素表示的能量强度 ${x_{l,f,t}}$是该频段上经过路径损耗(自由空间损耗)和阴影衰落(障碍物影响)的所有辐射源信号强度线性叠加得到的。频谱张量的Tucker秩表示电磁环境中辐射源的数量，核张量 $\mathcal{G}$表示辐射源功率，空间因子矩阵 ${\boldsymbol{S}}$表示辐射源与传感器之间的路径损耗系数，频率因子矩阵 ${\boldsymbol{U}}$表示辐射源的频率传播损耗系数。动态电磁环境中，辐射源位置随时间变化，辐射源与地理空间中障碍物的相对位置也随时间变化，导致不同程度的阴影衰落，因此时间因子矩阵 ${\boldsymbol{V}}$表示辐射源的阴影衰落损耗系数。综上所述，在张量Tucker分解的框架下求解缺失张量补全估计问题，可建模为如下的优化问题

本节将频谱地图构建任务转化为数据缺失的低秩张量补全问题，并给出式(5)的优化问题，在第4节中，将分别采用迭代交替最小二乘法和序列截断高阶奇异值分解法对问题式(5)进行求解，并设计高精度频谱地图构建算法以及快速频谱地图重建算法。

4.   问题求解

4.1   基于迭代交替最小二乘法的高精度频谱地图构建算法

式(6)的优化问题是对数据缺失的Tucker分解张量补全，求解使得近似误差的F范数最小化。该优化问题简写为

其中，为保证Tucker分解的本征唯一性，因子矩阵满足列正交 ${{\boldsymbol{S}}}^{\text{T}}\cdot {\boldsymbol{S}}={I}_{{R}_{1}\times {R}_{1}},\;{{\boldsymbol{U}}}^{\text{T}}\cdot {\boldsymbol{U}}={I}_{{R}_{2}\times {R}_{2}}, {{\boldsymbol{V}}}^{\text{T}}\cdot {\boldsymbol{V}}= {I}_{{R}_{3}\times {R}_{3}}$。在最优解的条件下，核张量满足： $\mathcal{G}= \mathcal{X}{\times }_{1}{{\boldsymbol{S}}}^{\text{T}}{\times }_{2}{{\boldsymbol{U}}}^{\text{T}}{\times }_{3}{{\boldsymbol{V}}}^{\text{T}}$。根据式(6)的优化问题，得到

优化目标可以重写为

将式(8)重写为矩阵形式得到：

其中， ${{\boldsymbol{A}}}^{\left(n\right)},\;n=1,2,3$分别表示3个因子矩阵， ${\boldsymbol{W}} = {{\boldsymbol{X}}_{\left( n \right)}}\left( {{{\boldsymbol{A}}^{\left( N \right)}} \otimes \cdots \otimes {{\boldsymbol{A}}^{\left( {n + 1} \right)}} \otimes {{\boldsymbol{A}}^{\left( {n - 1} \right)}} \otimes \cdots \otimes {{\boldsymbol{A}}^{\left( 1 \right)}}} \right)$。该问题通过交替最小二乘法(Alternating Least Squares, ALS)，转为对因子矩阵 ${\boldsymbol{S}}, \;{\boldsymbol{U}},\;{\boldsymbol{V}}$的一系列子问题。根据奇异值分解(Singular Value Decomposition, SVD)原理，求解的因子矩阵为 ${{\boldsymbol{Z}}^{\left( n \right)}}$的前 ${R_n}$个左奇异值向量，定义为

交替最小二乘法的流程为：根据设置的张量Tucker秩，初始化因子矩阵 ${\boldsymbol{S}},\; {\boldsymbol{U}},\;{\boldsymbol{V}}$，固定因子矩阵 ${\boldsymbol{U}}, {\boldsymbol{V}}$，利用式(10)求出因子矩阵 ${\boldsymbol{S}}$。同理，固定 ${\boldsymbol{S}}, {\boldsymbol{V}}$计算 ${\boldsymbol{U}}$，固定 ${\boldsymbol{S}},{\boldsymbol{ U}}$计算 ${\boldsymbol{V}}$，再求出核张量 $\mathcal{G}$。最后，根据式(3)，求出补全的估计张量 $\hat {\mathcal{X} }$。通过“补全-分解”的迭代使得算法收敛至误差最小，从而实现对张量的高精度补全。对于因子矩阵的初始化，可以随机初始化或者采用高阶奇异值分解(High Order Singular Value Decomposition, HOSVD)算法^[15]。上述使用的ALS算法需要预先设置Tucker秩。对张量秩的准确计算是NP-hard问题，难以设置准确的Tucker秩来执行算法。如果设置的秩 ${R_n} < {\rm{rank}} \left( {{{\boldsymbol{X}}_{\left( n \right)}}} \right)$，则称为截断秩，通过对核张量核因子矩阵进行截断操作同样得到低秩近似。张量的截断秩可视为超参数，截断秩的设置会影响张量补全的性能。对于本文研究频谱地图构建问题，张量的Tucker秩与电磁环境中辐射源的数量相关，在后续的仿真实验中验证了当截断秩的设置接近辐射源的数量时，频谱地图构建的精度更高，综上，基于交替最小二乘法的高精度频谱地图构建算法如算法1所示。

算法 1 基于迭代交替最小二乘法的高精度频谱地图构建算法
输入： $\mathcal{X} \in {\mathbb{R}^{L \times F \times T}}$，采样索引 ${\varOmega _T}$，截断秩 $\left( {{R_1},{R_2},{R_3}} \right)$
输出： $\hat {\mathcal{X}}$，核张量 $\mathcal{G}$，因子矩阵 ${\boldsymbol{S}},\; {\boldsymbol{U}}\;{\boldsymbol{V}}$, $t$时隙频谱地图 ${{\boldsymbol{X}}_T}$
初始化： ${\mathcal{X}^0} = {P_{{\Omega _T}}}\left( \mathcal{X} \right)$, ${\mathcal{D}_0} \leftarrow \mathcal{O}$, $i \leftarrow 0$，初始化因子矩阵 　 ${\boldsymbol{S}}\in {{\mathbb{R}}}^{S\times {R}_{1}}, {\boldsymbol{U}}\in {{\mathbb{R}}}^{F\times {R}_{2}}，{\boldsymbol{V}}\in {{\mathbb{R}}}^{T\times {R}_{3}}$
Repeat
${\mathcal{Z}^i} \leftarrow {\mathcal{X}^i}{ \times _2}{{\boldsymbol{U}}^{\text{T}}}{ \times _3}{{\boldsymbol{V}}^{\text{T}}}$
${\boldsymbol{S}} \leftarrow {\boldsymbol{Z}}_i^{(1)}$前 ${R_1}$个左奇异值向量
${\mathcal{Z}^i} \leftarrow {\mathcal{X}^i}{ \times _1}{{\boldsymbol{S}}^{\text{T}}}{ \times _3}{{\boldsymbol{V}}^{\text{T}}}$
${\boldsymbol{U}} \leftarrow {\boldsymbol{Z}}_i^{(2)}$前 ${R_2}$个左奇异值向量
${\mathcal{Z}^i} \leftarrow {\mathcal{X}^i}{ \times _1}{{\boldsymbol{S}}^{\text{T}}}{ \times _2}{{\boldsymbol{U}}^{\text{T}}}$
${\boldsymbol{V}} \leftarrow {\boldsymbol{Z}}_i^{(3)}$前 ${R_3}$个左奇异值向量
$\mathcal{G}\text{ }\leftarrow {\mathcal{X}}^{i}{\times }_{1}{{\boldsymbol{S}}}^{\text{T}}{\times }_{2}{{\boldsymbol{U}}}^{\text{T}}{\times }_{3}{{\boldsymbol{V}}}^{\text{T}}$
${\mathcal{D}^i} \leftarrow \mathcal{G}{ \times _1}{\boldsymbol{S}}{ \times _2}{\boldsymbol{U}}{ \times _3}{\boldsymbol{V}}$
更新对缺失数据的估计： ${\hat {\mathcal{X}}^i} \leftarrow {P_{{\Omega _T}}}\left( {{\mathcal{X}^0}} \right) + {P_{\left( { \sim {\Omega _T}} \right)}}\left( {{\mathcal{D}^i}} \right)$
$i \leftarrow i + 1$
Until $\frac{{\left\| {{{\hat {\mathcal{X}}}^i} - {{\hat {\mathcal{X}}}^{i - 1}}} \right\|_{\text{F}}^2}}{{\left\| {{{\hat {\mathcal{X}}}^i}} \right\|_{\text{F}}^2}} < \varepsilon$or $i > maxiterationtimes$
$\hat {\mathcal{X}} \leftarrow {\hat{ \mathcal{X}}^i}$
${{\boldsymbol{X}}_T} = {\hat {\mathcal{X}}_{:,:,T}}$

下载: 导出CSV 

| 显示表格

算法1的计算复杂度包括3个方面：根据因子矩阵交替计算 ${\mathcal{Z}^i}$产生的张量矩阵模态积运算，对 ${{\boldsymbol{Z}}^{\left( k \right)}}$进行SVD分解的计算以及 ${\mathcal{D}^i} \leftarrow \mathcal{G}{ \times _1}{\boldsymbol{S}}{ \times _2} {\boldsymbol{U}}{ \times _3}{\boldsymbol{V}}$。假设 ${\mathcal{X}^i}$的维度为 ${I_1} \times \cdots {I_N}$，则按照第 $k$模态展开后的矩阵尺寸为 ${I_k} \times {J_k}$，其中 $J_{k}=I_{1} \times \cdots I_{k-1} \times I_{k+1} \times \cdots I_{N}$，则计算 ${\mathcal{Z}^i}$的时间复杂度为 $O \left( {\displaystyle\sum\nolimits_k {I_k^2 \cdot J_k^2} } \right)$，SVD分解的时间复杂度为 $O\left( {\displaystyle\sum\nolimits_k {{I_k} \cdot \prod\nolimits_k {{I_k}} } } \right)$，计算 ${\mathcal{D}^i}$的时间复杂度为 $O\left( {\displaystyle\sum\nolimits_k {{r_k} \cdot {I_k}} } \right)$，其中 ${r_k}$为设置的截断秩。假设算法1达到收敛时的迭代次数为 ${\rm{iter}}$，则算法1的时间复杂度为 $O\left( {\rm{iter}} \cdot \left( \displaystyle\sum\nolimits_k {I_k^2 \cdot J_k^2} + \displaystyle \sum\nolimits_k {{I_k} \cdot \prod\nolimits_k {{I_k}} } \right) \right)$。

4.2   基于序列截断高阶奇异值分解的快速频谱地图构建算法

4.1节利用ALS算法求解数据缺失的低秩张量补全问题，该算法采用了循环迭代的方式，在算法收敛之前的迭代过程中，大量的张量矩阵模态积的运算花费相当的时间代价。此外，该算法需要多次迭代才能达到收敛，因此计算复杂度较高。为了解决这一问题，本节提出一种基于序列截断高阶奇异值分解(ST-HOSVD)的快速张量补全算法。该算法通过截断高阶奇异值分解找到张量 $\mathcal{X}$的低秩近似，使得已知数据上的重构误差较小，再将获得的所有低秩近似张量加权平均来获得最佳的补全结果。

首先，设置截断秩 $\left( {{R_1},{R_2},{R_3}} \right)$，对待补全张量 $\mathcal{X}$在第1模态进行截断操作，则因子矩阵 ${\boldsymbol{S}}$是 ${{\boldsymbol{X}}_{\left( 1 \right)}}$的左奇异值向量按照对应奇异值降序构成的矩阵。保留因子矩阵的前 ${R_1}$列，得到估计的因子矩阵 ${\boldsymbol{\hat S}} \in {\mathbb{R}^{L \times {R_1}}}$。临时核张量为 ${\mathcal{G}^1} = \mathcal{X}{ \times _1}{\boldsymbol{\hat S}}$，视为张量 ${\mathcal{X}_T}$在第1模态上的投影，则张量 ${\mathcal{X}_T}$的一个低秩近似为

对第2模态进行截断操作，计算出估计的因子矩阵 ${\boldsymbol{\hat U}} \in {\mathbb{R}^{F \times {R_2}}}$，临时核张量 ${\mathcal{G}^2} = \mathcal{X}{ \times _1}{\boldsymbol{\hat S}}{ \times _2}{\boldsymbol{\hat U}}$视为张量 $\mathcal{X}$在第1模态、第2模态上的投影，进而得到张量 $\mathcal{X}$的另一个低秩近似

最后，对第3模态截断操作，得到估计的因子矩阵 ${\boldsymbol{\hat V}} \in {\mathbb{R}^{T \times {R_3}}}$，临时核张量 ${\mathcal{G}^3} = \mathcal{X}{ \times _1}{\boldsymbol{\hat S}}{ \times _2}{\boldsymbol{\hat U}}{ \times _3}{\boldsymbol{\hat V}}$视为张量 $\mathcal{X}$在第1模态、第2模态和第3模态上的投影，得到张量 ${\mathcal{X}_T}$的第3个低秩近似

每个 ${\hat {\mathcal{T}}_i}$都是对待补全的张量 $\mathcal{X}$的一个低秩近似。通常张量分解算法取最后一个低秩近似项作为最终结果输出，如果得到若干个近似值，在没有其他先验信息的条件下，对 $\mathcal{X}$的最佳估计值为全部低秩近似的平均值。综上，基于序列截断高阶奇异值分解的快速频谱地图构建算法如算法2所示。

算法2　基于序列截断高阶奇异值分解的快速频谱地图构建算法
输入： ${\hat {\mathcal{X}}_{T - 1}}$， ${P_{{\Omega _T}}}\left( {{{\boldsymbol{X}}_T}} \right)$，截断秩 $\left( {{R_1},{R_2},{R_3}} \right)$
输出： ${\hat {\mathcal{X}}_T}$， $t$时隙频谱地图 ${{\boldsymbol{X}}_T}$
初始化： ${\mathcal{X}^0} = \left[ {{{\hat {\mathcal{X}}}_{T - 1}},{P_{{\Omega _T}}}\left( {{{\boldsymbol{X}}_T}} \right)} \right]$， ${\mathcal{D}^0} \leftarrow \mathcal{O}$， $i \leftarrow 0$
Repeat
使用HOSVD算法，对 ${\mathcal{X}^i}$依据截断秩进行分解，得到因子矩 　　　阵 ${\boldsymbol{S}}\in {{\mathbb{R}}}^{S\times {R}_{1}},\;{\boldsymbol{U}}\in {{\mathbb{R}}}^{F\times {R}_{2}},\,{\boldsymbol{V}}\in {{\mathbb{R}}}^{T\times {R}_{3}}$，临时核张量 　　　 ${\mathcal{G}^1} \leftarrow {\mathcal{X}^i}{ \times _1}{\boldsymbol{S}}$
根据式(11)计算张量 ${\mathcal{X}_T}$的第1个低秩近似 ${\hat {\mathcal{T}}^1}$
临时核张量 ${\mathcal{G}^2} \leftarrow {\mathcal{X}^i}{ \times _1}{\boldsymbol{S}}{ \times _2}{\boldsymbol{U}}$
根据式(12)计算张量 ${\mathcal{X}_T}$的第2个低秩近似 ${\hat {\mathcal{T}}^2}$
临时核张量 ${\mathcal{G}^3} \leftarrow {\mathcal{X}^i}{ \times _1}{\boldsymbol{S}}{ \times _2}{\boldsymbol{U}}{ \times _3}{\boldsymbol{V}}$
根据式(13)计算张量 ${\mathcal{X}_T}$的第3个低秩近似 ${\hat {\mathcal{T}}^3}$
计算低秩近似的平均值 ${\mathcal{D}^i} = \dfrac{1}{3}\left( {{{\hat {\mathcal{T}}}^1} + {{\hat {\mathcal{T}}}^2} + {{\hat {\mathcal{T}}}^3}} \right)$
更新对缺失数据的估计： ${\hat {\mathcal{X}}^i} = {P_{{\Omega _T}}}\left( {{\mathcal{X}^0}} \right) + {P_{( \sim {\Omega _T})}}\left( {{\mathcal{D}^i}} \right)$
Until $\frac{{\left\| {{{\hat {\mathcal{X}}}^i} - {{\hat {\mathcal{X}}}^{i - 1}}} \right\|_{\text{F}}^2}}{{\left\| {{{\hat {\mathcal{X}}}^i}} \right\|_{\text{F}}^2}} < \varepsilon$ or $i > {\rm{maxiterationtimes}}$
${\hat {\mathcal{X}}_T} \leftarrow {\hat {\mathcal{X}}^i}$
${{\boldsymbol{X}}_T} \leftarrow \hat {\mathcal{X}}_{:,:,T}^i$

下载: 导出CSV 

| 显示表格

假设 ${\mathcal{X}^i}$的维度为 ${I_1} \times \cdots {I_N}$，则按照第 $k$模态展开后的矩阵尺寸为 ${I_k} \times {J_k}$，则 ${\mathcal{X}^i}$的SVD分解的时间复杂度为 $O\left( {\displaystyle\sum\nolimits_k {{I_k} \cdot \prod\nolimits_k {{I_k}} } } \right)$。计算低秩近似张量 ${\widehat{\mathcal{T}}}^{k},\;k=1,2,3$的时间复杂度为 $O\left( {\displaystyle\sum\nolimits_k {{I_k} \cdot \prod\nolimits_k {{I_k}} } } \right)$。计算 ${\mathcal{D}^i}$以及 ${\hat {\mathcal{X}}^i}$的时间复杂度为 $O\left( {\displaystyle\prod\nolimits_k {{I_k}} } \right)$。假设算法2达到收敛时的迭代次数为 ${\rm{iter}}$，则算法2的时间复杂度为 $O\left( {{\rm{iter}} \cdot \displaystyle\sum\nolimits_k {{I_k} \cdot \prod\nolimits_k {{I_k}} } } \right)$。

5.   仿真实验与分析

5.1   仿真环境设置

本节提供了数值仿真结果以评估本文提出的两种频谱地图构建算法的性能。本文使用如图3(a)所示的法兰克福的部分城市地形数据，利用电磁波传播模拟软件WinProp模拟部署辐射源和传感器，以构建城市电磁波传播环境。为了验证电磁仿真场景的实用性和算法在不同环境下的泛化能力，在图3(a)的环境内随机选取边长为100 m的待监测区域，并离散为n=100的小网格，频谱地图的空间分辨率为1 m，如图3(b)所示。在待监测区域内随机部署4个移动的辐射源，运动速率1 m/s，高度为1.5 m，工作在1800～2000 MHz频段上，频率分辨率为1 MHz。定义空间位置采样率为 $r = {{{n_r}} \mathord{\left/ {\vphantom {{{n_r}} {{n^2}}}} \right. } {{n^2}}}$，其中 ${n_r}$是部署传感器的网格数， ${n^2}$是待检测区域全部网格的数量。根据设定的空间采样率在待监测区域内部署相应数量的传感器接收信号，用于构建完整的频谱地图，传感器部署位置是随机均匀选取的。考虑移动辐射源的运动状态，每1 s生成1张频谱地图，持续观测100 s，获得的3阶频谱张量的维度为 $\left(10\; 000, 200,100\right)$。仿真生成的完整无缺失的张量可以作为频谱地图重建的基础。为了评价频谱地图重建的精度，采用均方根误差(Relative Mean Square Error, RMSE)作为性能评价指标

图 3  仿真场景示意图

下载: 全尺寸图片 幻灯片

其中 ${{\boldsymbol{X}}_t},{{\boldsymbol{\hat X}}_t}$分别为 $t$时隙的原始频谱地图和估计的频谱地图， $N$为频谱地图的元素数量。为了对比本文提出算法的性能，引入了NCARL算法^[16]和TS1算法^[17]作为基准对比算法，其中NCARL算法和TS1算法的时间复杂度均为 $O\left( {{\rm{iter}} \cdot T \cdot {{(n)}^{\tfrac{3}{2}}}} \right)$， ${\rm{iter}}$是迭代次数。

5.2   性能评估

本文提出的两种频谱地图构建算法均要预先设置张量的Tucker秩，对于 $N$阶张量，需要分别指定 $N$阶的秩，算法调优的过程和实施的过程都需要考虑对秩的设置。图4研究了张量截断秩对所提出的频谱地图构建算法性能的影响。为了验证辐射源运动对算法性能的影响，在仿真中加入静止辐射源场景作为对比。仿真结果表明，在相同空间采样率的条件下，随着截断秩的增加，算法性能先上升后下降。并且当辐射源保持静止，高精度构建算法在截断秩设置为5时，算法性能达到最优；快速构建算法的截断秩设置为4时，算法性能达到最优。当辐射源移动，形成动态频谱环境时，两种算法性能达到最优时的截断秩分别为8和7。这是因为在动态电磁环境中，不同时隙的频谱地图按照时序堆叠后，移动的辐射源被视为多个等效辐射源，此时的频谱地图是多个等效辐射源线性叠加而成，这导致了3阶频谱张量的Tucker秩的变化。因此，在算法的实际部署应用中，需要对张量Tucker秩进行调优，以实现最佳的频谱地图构建精度。

图 4  张量截断秩对频谱地图构建精度的影响

下载: 全尺寸图片 幻灯片

本文研究了不同空间采样率和背景噪声对频谱地图构建精度的影响，仿真结果如图5所示。根据图4的结论，将高精度构建算法和快速构建算法的截断秩设置为8和7，使得两种频谱地图构建算法均达到最佳性能。在不同的背景噪声条件下，随着空间采样率的增加，高精度构建算法和快速构建算法的性能显著提升，随后保持平稳。当采样率小于0.05时，信息丢失过多导致构建的频谱地图误差较大，当采样率大于0.2时，信息冗余，构建的频谱地图精度提升有限，采样成本显著提高。在仿真实验中，TS1算法没有给出采样率小于5%时的性能曲线，因为该算法无法在这样低的采样率下运行，并且NCARL算法在采样率小于0.2时的性能较差，难以构建出可用的频谱地图。而本文提出的频谱构建算法在采样率为0.05时，即可重构出较为精确的频谱地图。在实际应用场景中，本文提出的算法能够显著降低传感器的数量，从而降低监测网络的构建成本。同时还能观察到，当背景噪声功率小于–30 dBm时，对4种算法性能的影响几乎可以忽略，而当噪声功率达到–20 dBm时，4种算法的性能均有显著下降。此外，在所有背景噪声设置下，本文提出的两种频谱地图构建算法的精度均显著优于对比算法。噪声功率为–40 dBm, –30 dBm, –20 dBm，空间采样率为0.05时，高精度算法的频谱地图构建精度误差为–18.02 dB, –15.62 dB, –13.44 dB，快速算法的频谱地图构建精度为–16.76 dB, –15.4 dB, –12.07 dB，本文提出的两种算法具有更高的噪声鲁棒性，在较高的噪声水平下仍能正常工作。

图 5  不同噪声水平频谱地图构建算法性能比较

下载: 全尺寸图片 幻灯片

本文还研究了不同算法在时间复杂度上的性能比较，以验证上节给出的算法时间复杂度计算公式，其中TS1算法和NCARL算法不需要多次迭代，仅给出算法运行时间消耗的对比。从图6(a)中可以看出，在背景噪声为–40 dBm的条件下，随着空间采样率的降低，高精度构建算法和快速构建算法达到收敛时所需的迭代次数增加。这是因为缺失的元素数量大，需要多次分解重建才能达到设定的频谱地图精度。从图中还能够看出，在0.05的空间采样率条件下，高精度构建算法迭代22次达到收敛，能够实现–18.02 dB的构建精度误差；快速构建算法仅需6次迭代即可达到收敛，能够实现–16.76 dB的构建精度误差。图6(b)中给出了不同算法构建频谱地图的时间消耗，可以看出，NCARL算法的运行时间消耗在空间采样率小于0.1时会随着空间采样率的增加而迅速增加，当空间采样率大于0.1时，该算法的运行时间消耗相对平稳。当采样率大于0.05时，TS1算法的运行时间消耗是所有算法中最大的，并且在采样率大于0.2之后保持平稳。本文提出的快速构建算法的运行时间消耗在空间采样率大于0.05时最低，并且随着采样率的增大，运行时间不断降低，这是因为需要估计重建的元素数量减少，算法运行迭代次数少。高精度构建算法在空间采样率小于0.05时运行时间消耗最大，因为大量需要重建估计的元素使得算法需要多次迭代，导致计算时间较长。然而，随着空间采样率的增加，该算法的运行时间消耗迅速降低，当空间采样率大于0.2时，高精度算法的计算时间消耗小于NCARL算法和TS1算法。根据上述算法性能分析，在实际应用中可以根据不同的构建精度需求和硬件条件选择最佳的算法进行频谱地图的构建。

图 6  不同算法时间复杂度的性能比较

下载: 全尺寸图片 幻灯片

最后，图7给出了4种算法在时间 $t = 10$时的频谱地图的可视化效果。与传统算法相比，在–40 dBm的背景噪声条件下，本文提出的高精度频谱地图构建算法和快速频谱地图构建算法能以更少的传感器采样数量实现更好的频谱地图构建效果，这与图5的性能结果一致。从可视化效果能够看出，本文提出的构建算法能够获得更加精确的频谱地图，能清晰地反映出辐射源信号强度、辐射源位置、信号空白区域和信号覆盖区域。不仅显著提升了频谱地图在频谱管理、网络规划、干扰协调、频谱管理等常规任务中的作用，还能够在目标搜索和多辐射源定位任务中实现更高的定位精度。

图 7  不同算法构建频谱地图可视化效果

下载: 全尺寸图片 幻灯片

6.   结束语

本文研究了使用少量监测样本构建动态电磁环境频谱地图的问题，将动态电磁环境的时变频谱地图建模为3维频谱张量，通过张量Tucker分解提取低维特征并给出其物理意义，设计一种基于Tucker分解的低秩张量补全模型，并开发两种无需先验信息的频谱地图构建算法对模型求解，在5%的空间采样率下，实现了对频谱地图的高精度和快速重建。本文提出的两种算法能够在更低的采样率条件下构建出误差更小精度更高的频谱地图，并且具有良好的噪声鲁棒性，能显著提升在频谱管理和辐射源定位等任务中的作用。此外，本文首次给出了符合Tucker分解的频谱地图构建模型，在仿真实验中验证了可行性。下一步将继续深入研究Tucker分解与动态电磁环境频谱地图构建模型之间的关系。此外，时序频谱数据的存储的长度会影响频谱地图构建的精度，在未来的工作中将面向采样率设计一种动态加窗算法，通过逐步淘汰过时数据，增加新到达数据的权重，从而提高更新算法的性能。