基于数字孪生的多自动驾驶车辆分布式协同路径规划算法

唐伦; 戴军; 成章超; 张鸿鹏; 陈前斌

doi:10.11999/JEIT230678

基于数字孪生的多自动驾驶车辆分布式协同路径规划算法

doi: 10.11999/JEIT230678

1.
重庆邮电大学通信与信息工程学院重庆 400065
2.
移动通信技术重庆市重点实验室重庆 400065

基金项目: 国家自然科学基金(62071078)，川渝联合实施重点研发项目(2021YFQ0053)

详细信息

作者简介:
唐伦：男，教授，博士生导师，研究方向为新一代无线通信网络、异构蜂窝网络、软件定义无线网络等

戴军：男，硕士生，研究方向为自动驾驶的路径规划、数字孪生、联邦学习优化等

成章超：男，硕士生，研究方向为车联网、数字孪生、深度强化学习等

张鸿鹏：男，硕士生，研究方向为车联网中的网络切片、数字孪生、资源分配策略等

陈前斌：男，教授，博士生导师，研究方向为个人移动通信、多媒体信息处理与传输、下一代移动通信网络、异构蜂窝网络等

通讯作者:
戴军　878607471@qq.com

中图分类号: TN929.5
计量
- 文章访问数: 261
- HTML全文浏览量: 403
- PDF下载量: 61
- 被引次数: 0
出版历程
- 收稿日期: 2023-07-07
- 修回日期: 2024-01-04
- 网络出版日期: 2024-01-29
- 刊出日期: 2024-06-30

Distributed Collaborative Path Planning Algorithm for Multiple Autonomous vehicles Based on Digital Twin

1.
School of Communications and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
2.
Chongqing Key Laboratory of Mobile Communications Technology, Chongqing 400065, China

Funds: The National Natural Science Foundation of China (62071078), Sichuan and Chongqing Key R&D Projects (2021YFQ0053)

摘要

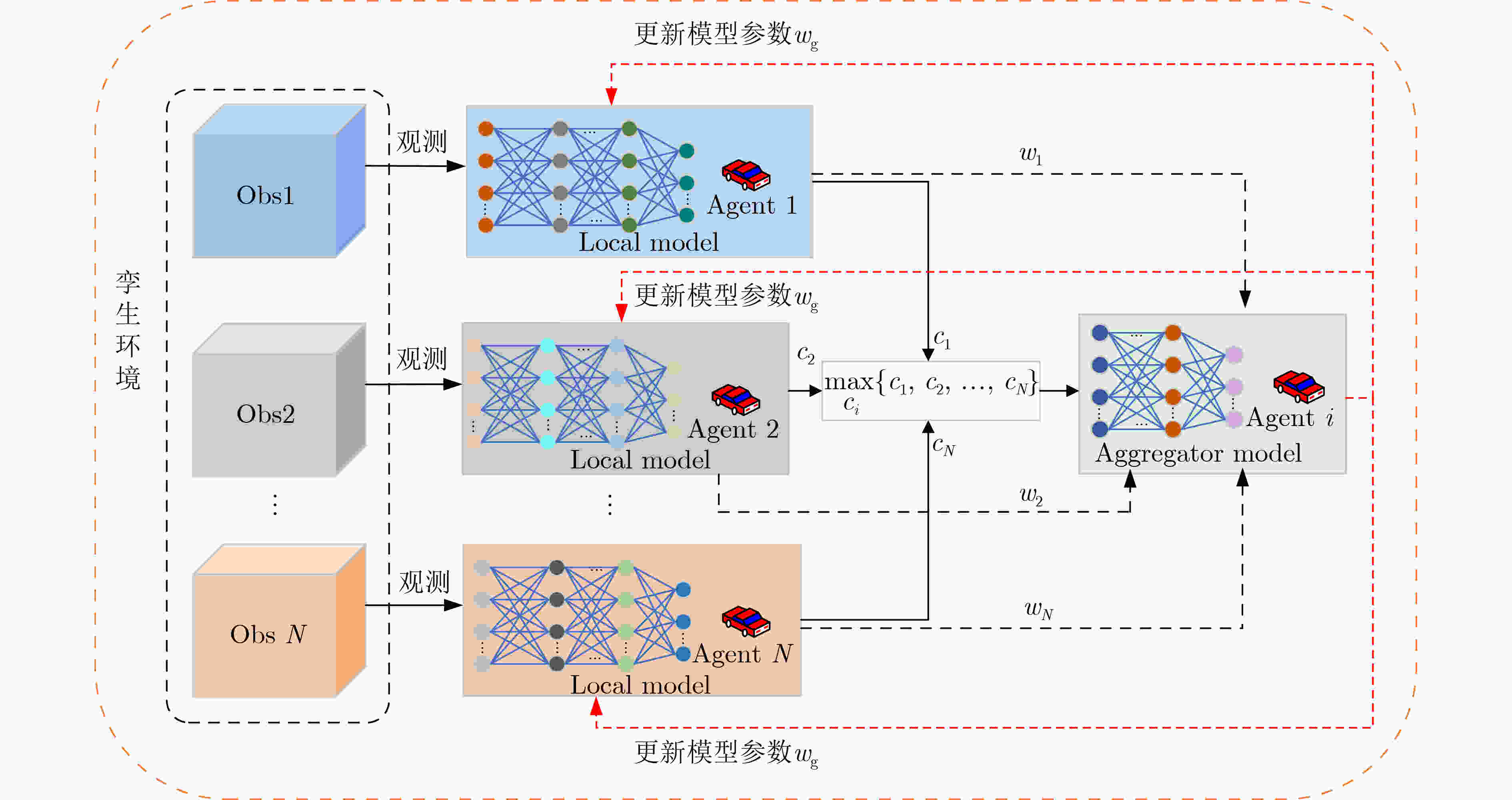
摘要: 针对多辆自动驾驶车辆(AVs)在进行路径规划过程中存在的车辆之间协作难、协作训练出来的模型质量低以及所求结果直接应用到物理车辆的效果较差的问题，该文提出一种基于数字孪生(DT)的多AVs分布式协同路径规划算法，基于可信度加权去中心化的联邦强化学习方法(CWDFRL)来实现多AVs的路径规划。首先将单个AVs的路径规划问题建模成在驾驶行为约束下的最小化平均任务完成时间问题，并将其转化成马尔可夫决策过程(MDP)，使用深度确定性策略梯度算法(DDPG)进行求解；然后使用联邦学习(FL)保证车辆之间的协同合作，针对集中式的FL中存在的全局模型更新质量低的问题，使用基于可信度的动态节点选择的去中心化FL训练方法改善了全局模型聚合质量低的问题；最后使用DT辅助去中心化联邦强化学习(DFRL)模型的训练，利用孪生体可以从DT环境中学习的优点，快速将训练好的模型直接部署到现实世界的AVs上。仿真结果表明，与现有的方法相比，所提训练框架可以得到一个较高的奖励，有效地提高了车辆对其本身速度的利用率，与此同时还降低了车辆群体的平均任务完成时间和碰撞概率。
- 数字孪生 /
- 自动驾驶 /
- 去中心化联邦强化学习 /
- 路径规划
Abstract: Focusing on the problems of difficult cooperation between vehicles, low quality of the model trained by cooperation and poor effect of direct application of the obtained results to physical vehicles in the process of path planning for multiple Autonomous Vehicles (AVs), a distributed collaborative path planning algorithm is proposed for multiple AVs based on Digital Twin (DT). The algorithm is based on the Credibility-Weighted Decentralized Federated Reinforcement Learning (CWDFRL) to realize the path planning of multiple AVs. In this paper, the path planning problem of a single AVs is first modeled as the problem of minimizing the average task completion time under the constraints of driving behavior, which is transformed into Markov Decision Process (MDP) and solved by Deep Deterministic Policy Gradient algorithm (DDPG). Then Federated Learning (FL) is used to ensure the cooperation between vehicles. Aiming at the problem of low quality of global model update in centralized FL, this paper uses a decentralized FL training method based on dynamic node selection of reliability to improve the low quality. Finally, the DT is used to assist the training of the Decentralized Federated Reinforcement Learning (DFRL) model, and the trained model can be quickly deployed directly to the real-world AVs by taking advantage of the twin’s ability of learning from DT environment. The simulation results show that compared with the existing methods, the proposed training framework can obtain a higher reward, effectively improve the utilization of the vehicle’s own speed, and at the same time reduce the average task completion time and collision probability of the vehicle swarm.
- Digital Twin (DT) /
- Autonomous driving /
- Decentralized Federated Reinforcement Learning (DFRL) /
- Path planning

HTML全文

图 1 系统框图

下载: 全尺寸图片幻灯片

图 2 DT-CWDFRL训练框架

下载: 全尺寸图片幻灯片

图 3 平均累计奖励

下载: 全尺寸图片幻灯片

图 4 损失值对比

下载: 全尺寸图片幻灯片

图 5 车辆群体平均碰撞概率

下载: 全尺寸图片幻灯片

图 6 车辆群体归一化平均转向角

下载: 全尺寸图片幻灯片

图 7 车辆群体平均任务完成时间

下载: 全尺寸图片幻灯片

图 8 车辆群体归一化平均速度

下载: 全尺寸图片幻灯片

1 本地车辆训练算法

输入：车辆数$ N $，噪声$ n $，全局模型参数$ {w_g} = ({\pi _g},{\theta _g}) $
输出：每个车辆训练模型的可信度$ {c_i} $
(1) for $ {\mathrm{vehicle}} \in 1,2, \cdots ,N $ do
(2) 　将全局模型参数同步到本地运行的DDPG网络
(3) 　根据当前环境做出动作，并增添随机噪声进行探索：　　　 $ {\boldsymbol{a}}(t) = \pi ({\boldsymbol{s}}(t)\|{\theta ^\pi }) + {\boldsymbol{n}} $
(4) 　执行动作$ {\boldsymbol{a}}(t) $，得到状态$ {\boldsymbol{s}}(t + 1) $以及奖励$ r(t) $
(5) 　if 经验回放池还没存满 then
(6) 　　将$ \left( {{\boldsymbol{s}}(t),{\boldsymbol{a}}(t),r(t),{\boldsymbol{s}}(t + 1)} \right) $存入经验回放池中
(7) 　else
(8) 　　用$ \left( {{\boldsymbol{s}}(t),{\boldsymbol{a}}(t),{\boldsymbol{r}}(t),{\boldsymbol{s}}(t + 1)} \right) $代替经验池中的经验
(9) 　end if
(10) 　从经验池中随机选择batch-size条经验构成样本
(11) 　通过目标评论家网络得到$ Q({\boldsymbol{s}}(t + 1),{\boldsymbol{a}}(t + 1)\|{\theta ^{Q'}}) $，　　　　计算损失函数$ L({\theta ^Q}) $
(12) 　然后更新估计评论家网络参数$ {\theta ^Q} $
(13) 　根据估计评论家网络得到$ Q\left( {{\boldsymbol{s}}(t),{\boldsymbol{a}}(t)\|{\theta ^Q}} \right) $，用策略梯　　　　度更新估计行动家网络参数$ {\theta ^\pi } $
(14) 　软更新目标行动家网络和目标评论家网络的参数　　　　 $ {\theta ^{\pi '}},{\theta ^{Q'}} $
(15) 　通过式(13)计算出车辆节点的可信度$ {c_i} $
(16)end for

下载: 导出CSV

2 车辆协同训练算法

输入：回合数$ M $，每回合训练次数$ {\mathrm{step}}\_{\mathrm{per}}\_{\mathrm{episode}} $，车辆数$ N $，聚合周期$ {A_{\mathrm{g}}} $
输出：最优策略$ {\pi ^*} $
(1) for $ {\mathrm{episode}} = 1,2, \cdots ,M $ do
(2) 　为每辆车初始化全局模型参数$ {w_{\mathrm{g}}} = ({\pi _{\mathrm{g}}},{\theta _{\mathrm{g}}}) $
(3) 　初始化环境$ s(0) $
(4) 　for $ {\mathrm{step}} \in {\mathrm{step}}\_{\mathrm{per}}\_{\mathrm{episode}} $ do
(5) 　　for $ {\mathrm{vehicle}} \in 1,2, \cdots ,N $ do
(6) 　　　调用算法1，得到每个车辆节点训练模型的可信度$ {c_i} $
(7) 　　　if 处于聚合周期$ {A_{\mathrm{g}}} $，则需要进行全局模型的更新
(8) 　　　　选择聚合节点，聚合全局模型$ {w_{\mathrm{g}}} = ({\pi _{\mathrm{g}}},{\theta _{\mathrm{g}}}) $
(9) 　　　　使用全局模型权重$ {w_{\mathrm{g}}} = ({\pi _{\mathrm{g}}},{\theta _{\mathrm{g}}}) $来更新　　　　　　　$ {\theta ^\pi },{\theta ^Q},{\theta ^{\pi '}},{\theta ^{Q'}} $
(10) 　　　end if
(11) 　　end for
(12) 　end for
(13) end for

下载: 导出CSV

表 1 CWDF-DDPG仿真参数

仿真参数	值	仿真参数	值
经验池大小批尺寸折扣因子价值网络学习率策略网络学习率软更新系数最大回合数隐藏层单元数聚合周期免碰撞的最小安全时间	100000 128 0.99 0.001 0.0001 0.01 10000 256 5 2.5s	AVs的速度范围 HDV的数量碰撞系数($ {w_{\mathrm{c}}} $) 连接系数($ {w_{{\mathrm{connec}}}} $) 接近目标系数($ {w_1} $) 舒适度奖励系数($ {w_2} $) 效率奖励系数($ {w_3} $) AVs之间的安全距离($ {d_1} $) AVs与HDV的安全距离($ {d_2} $) AVs的最大通信距离($ {d_3} $)	[0,15] 10 –50 0.2 0.1 1 1 2m 2m 50m

下载: 导出CSV

参考文献(15)

[1]	KIRAN B R, SOBH I, TALPAERT V, et al. Deep reinforcement learning for autonomous driving: A survey[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(6): 4909–4926. doi: 10.1109/TITS.2021.3054625.
[2]	LI Yanqiang, MING Yu, ZHANG Zihui, et al. An adaptive ant colony algorithm for autonomous vehicles global path planning[C]. 2021 IEEE 24th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Dalian, China, 2021: 1117–1122. doi: 10.1109/CSCWD49262.2021.9437682.
[3]	ZHOU Jian, ZHENG Hongyu, WANG Junmin, et al. Multiobjective optimization of lane-changing strategy for intelligent vehicles in complex driving environments[J]. IEEE Transactions on Vehicular Technology, 2020, 69(2): 1291–1308. doi: 10.1109/TVT.2019.2956504.
[4]	ZHU Gongsheng, PEI Chunmei, DING Jiang, et al. Deep deterministic policy gradient algorithm based lateral and longitudinal control for autonomous driving[C]. 2020 5th International Conference on Mechanical, Control and Computer Engineering (ICMCCE), Harbin, China, 2020: 740–745. doi: 10.1109/ICMCCE51767.2020.00163.
[5]	SHI Dian, DING Jiahao, ERRAPOTU S M, et al. Deep Q-network-based route scheduling for TNC vehicles with passengers’ location differential privacy[J]. IEEE Internet of Things Journal, 2019, 6(5): 7681–7692. doi: 10.1109/JIOT.2019.2902815.
[6]	KHALIL A A and RAHMAN M A. FED-UP: Federated deep reinforcement learning-based UAV path planning against hostile defense system[C]. 2022 18th International Conference on Network and Service Management (CNSM), Thessaloniki, Greece, 2022: 268–274. doi: 10.23919/CNSM55787.2022.9964907.
[7]	LI Yijing, TAO Xiaofeng, ZHANG Xuefei, et al. Privacy-preserved federated learning for autonomous driving[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(7): 8423–8434. doi: 10.1109/TITS.2021.3081560.
[8]	唐伦, 文明艳, 单贞贞, 等. 移动边缘计算辅助智能驾驶中基于高效联邦学习的碰撞预警算法[J]. 电子与信息学报, 2023, 45(7): 2406–2414. doi: 10.11999/JEIT220797. TANG Lun, WEN Mingyan, SHAN Zhenzhen et al. Collision warning algorithm based on efficient federated learning in mobile edge computing assisted intelligent driving[J]. Journal of Electronics & Information Technology, 2023, 45(7): 2406–2414. doi: 10.11999/JEIT220797.
[9]	KARRAS A, KARRAS C, GIOTOPOULOS K C, et al. Peer to peer federated learning: Towards decentralized machine learning on edge devices[C]. 2022 7th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Ioannina, Greece, 2022: 1–9. doi: 10.1109/SEEDA-CECNSM57760.2022.9932980.
[10]	SHEN Gaoqing, LEI Lei, LI Zhilin, et al. Deep reinforcement learning for flocking motion of multi-UAV systems: Learn from a digital twin[J]. IEEE Internet of Things Journal, 2022, 9(13): 11141–11153. doi: 10.1109/JIOT.2021.3127873.
[11]	GLAESSGEN E and STARGEL D. The digital twin paradigm for future NASA and U. S. air force vehicles[C]. The 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, Hawaii, 2012: 1818. doi: 10.2514/6.2012-1818.
[12]	TAO Fei, ZHANG He, LIU Ang, et al. Digital twin in industry: State-of-the-art[J]. IEEE Transactions on Industrial Informatics, 2019, 15(4): 2405–2415. doi: 10.1109/TII.2018.2873186.
[13]	唐伦, 贺兰钦, 谭颀, 等. 基于深度确定性策略梯度的虚拟网络功能迁移优化算法[J]. 电子与信息学报, 2021, 43(2): 404–411. doi: 10.11999/JEIT190921. TANG Lun, HE Lanqin, TAN Qi, et al. Virtual network function migration optimization algorithm based on deep deterministic policy gradient[J]. Journal of Electronics & Information Technology, 2021, 43(2): 404–411. doi: 10.11999/JEIT190921.
[14]	LIN Qifeng and LING Qing. Byzantine-robust federated deep deterministic policy gradient[C]. ICASSP 2022 - 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 2022: 4013–4017. doi: 10.1109/ICASSP43922.2022.9746320.
[15]	MA Xu, SUN Xiaoqian, WU Yuduo, et al. Differentially private byzantine-robust federated learning[J]. IEEE Transactions on Parallel and Distributed Systems, 2022, 33(12): 3690–3701. doi: 10.1109/TPDS.2022.3167434.