结合深度强化学习的边缘计算网络服务功能链时延优化部署方法

孙春霞; 杨丽; 王小鹏; 龙良

doi:10.11999/JEIT230632

结合深度强化学习的边缘计算网络服务功能链时延优化部署方法

doi: 10.11999/JEIT230632

兰州交通大学电子与信息工程学院兰州 730070

基金项目: 甘肃省高校产业支撑计划(2023CYZC-40)，甘肃省优秀研究生“创新之星”项目(2023CXZX-546)

详细信息

作者简介:
孙春霞：女，副教授，研究方向为电路与系统

杨丽：女，硕士生，研究方向为信号处理、网络功能虚拟化、强化学习和资源分配

王小鹏：男，教授，研究方向为信息与通信工程、智能化信息处理等

龙良：男，硕士生，研究方向为室内定位、人工智能

通讯作者:
杨丽　2980094475@qq.com

中图分类号: TN929.5; TP393
计量
- 文章访问数: 326
- HTML全文浏览量: 297
- PDF下载量: 57
- 被引次数: 0
出版历程
- 收稿日期: 2023-06-26
- 修回日期: 2023-11-06
- 网络出版日期: 2023-11-13
- 刊出日期: 2024-04-24

Optimized Deployment Method of Edge Computing Network Service Function Chain Delay Combined with Deep Reinforcement Learning

School of Electronics and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China

Funds: Gansu Province Higher Education Industry Support Plan Project (2023CYZC-40), Gansu Province Excellent Graduate 'Innovation Star' Program (2023CXZX-546)

摘要

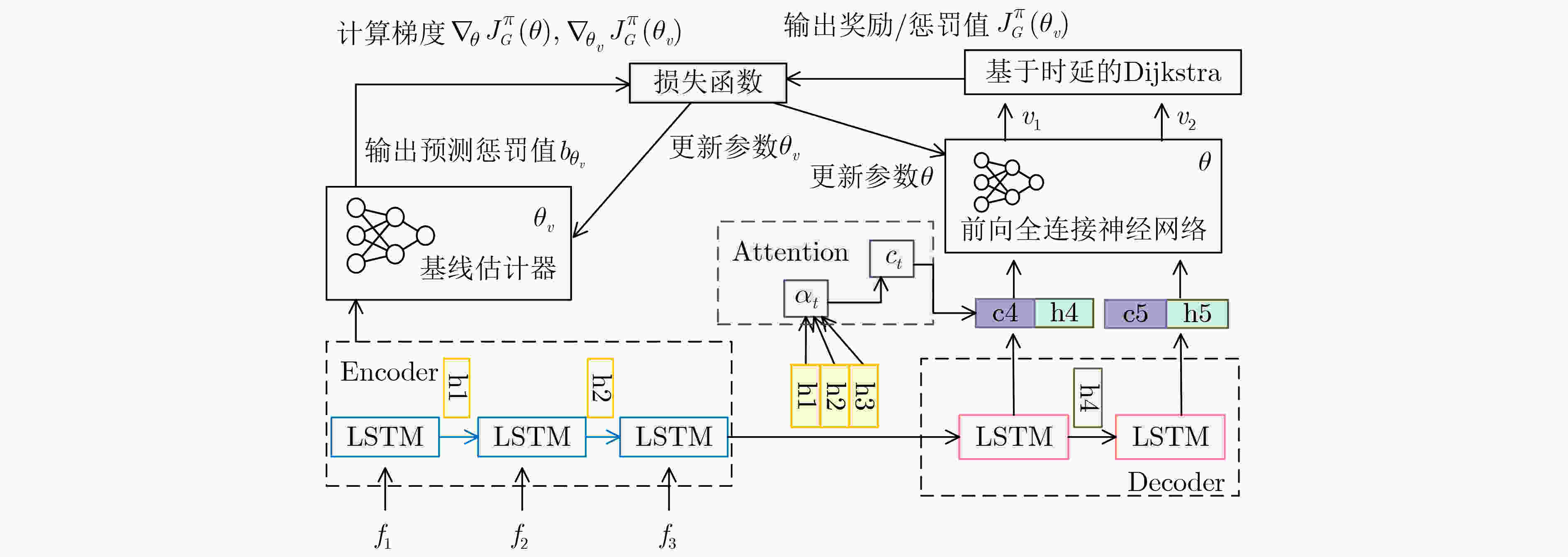
摘要: 该文针对边缘网络资源受限且对业务流端到端时延容忍度低的问题，结合深度强化学习与基于时延的Dijkstra寻路算法提出一种面向时延优化的服务功能链(SFC)部署方法。首先，设计一种基于注意力机制的序列到序列(Seq2Seq)代理网络和基于时延的Dijkstra寻路算法，用于产生虚拟网络功能(VNF)的部署以及服务SFC的链路映射，同时考虑了时延优化模型的约束问题，采用拉格朗日松弛技术将其纳入强化学习目标函数中；其次，为了辅助网络代理快速收敛，采用基线评估器网络评估部署策略的预期奖励值；最后，在测试阶段，通过贪婪搜索及抽样技术降低网络收敛到局部最优的概率，从而改进模型的部署。对比实验表明，该方法在网络资源受限的情况下，比First-Fit算法与TabuSearch算法的时延分别降低了约10%和86.3%，且较这两种算法稳定约74.2%与84.4%。该方法能较稳定地提供更低时延的端到端服务，使时延敏感类业务获得更好体验。
- 服务功能链部署 /
- 深度强化学习 /
- 边缘网络 /
- 端到端时延
Abstract: A delay-optimized Service Function Chain (SFC) deployment approach is proposed by combining deep reinforcement learning with the delay-based Dijkstra pathfinding algorithm for the problem of resource-constrained edge networks and low end-to-end delay tolerance for service flows. Firstly, an attention mechanism-based Sequence to Sequence (Seq2Seq) agent network and a delay-based Dijkstra pathfinding algorithm are designed for generating Virtual Network Function(VNF) deployments and link mapping for SFC, while the constraint problem of the delay optimization model is considered and incorporated into the reinforcement learning objective function using Lagrangian relaxation techniques; Secondly, to assist the network agent in converging quickly, a baseline evaluator network is used to assess the expected reward value of the deployment strategy; Finally, in the testing phase, the deployment strategy of the agent is improved by reducing the probability of convergence of the network to a local optimum through greedy search and sampling techniques. Comparison experiments show that the method reduces the latency by about 10% and 86.3% than the First-Fit algorithm and TabuSearch algorithm, respectively, and is about 74.2% and 84.4% more stable than these two algorithms in the case of limited network resources. This method provides a more stable end-to-end service with lower latency, enabling a better experience for latency-sensitive services.
- Service Function Chain(SFC) deployment /
- Deep reinforcement learning /
- Edge networks /
- End-to-end latency

HTML全文

图 1 DDRL学习框架

下载: 全尺寸图片幻灯片

图 2 网络代理的训练过程

下载: 全尺寸图片幻灯片

图 3 小型网络场景中各算法生成策略的服务时延对比

下载: 全尺寸图片幻灯片

图 4 3种算法在大型网络场景下生成的放置策略的时延对比

下载: 全尺寸图片幻灯片

图 5 3种算法在不同网络场景下的运算时长

下载: 全尺寸图片幻灯片

图 6 DDRL与FF的时延优劣数量比较

下载: 全尺寸图片幻灯片

图 7 3种算法时延的算术平均值以及平均方差

下载: 全尺寸图片幻灯片

算法1　结合基于时延的Dijkstra与DRL算法的训练过程
输入：网络服务请求${s_i}$和网络状态信息；惩罚权重${\alpha _{{\rm{occupancy}}}}$, ${\alpha _{{\rm{bandwidth}}}}$；环境时延的相关参数； epoch, batch；
输出：SFC的部署策略${p^{{s_i}}}$，以及业务请求的端到端时延预估值
DDRL训练过程：
(1) 初始化参数$\theta $, ${\theta _v}$；$p \leftarrow \varnothing $, $\varOmega \leftarrow 0$, ${l_i} \leftarrow \varnothing $ , ${s_i} \leftarrow \varnothing $, $L\left( {p\|s} \right) \leftarrow 0$和循环次数epoch
(2) for epoch = 1, 2 ,···, do
(3) 　　重置梯度${\mathrm{d}}\theta \leftarrow 0$
(4) 　　生成batch个SFC实例$S$；根据式(11)计算的概率为VNF${f_i}$选择部署位置${v_i} \in {V^P}$
(5) 　　由基于时延的Dijkstra寻路算法为各VNF${f_i}$找到时延最小的路径树${l_i}$
(6) 　　${s_j}$～对输入$S$进行采样，$j \in \left\{ {1,2,\cdots,B} \right\}$；${p_j}$对相应策略${\pi _\theta }$ 进行抽样，$j \in \left\{ {1,2,\cdots,B} \right\}$
(7) 　　采样得到的${s_j}$通过基线估计器预估奖励${b_j} \leftarrow {b_{{\theta _v}}}\left( {{s_j}} \right)$,$j \in \left\{ {1,2,\cdots,B} \right\}$
(8) 　　计算真实奖励$G\left( {{p_j}} \right)$、根据式(11)计算近似梯度${\nabla _\theta }J_G^\pi \left( \theta \right)$
(9) 　　根据式(15)计算预测奖励值${b_j}$与真实奖励值$G\left( {{p_j}} \right)$均方误差${\nabla _{{\theta _v}}}J_G^\pi \left( {{\theta _v}} \right)$
(10) 　 $\theta \leftarrow {\mathrm{Adam}}\left( {\theta ,{\nabla _\theta }J_G^\pi \left( \theta \right)} \right)$, ${\theta _v} \leftarrow {\mathrm{Adam}}\left( {{\theta _v},{\nabla _{{\theta _v}}}J_G^\pi \left( {{\theta _v}} \right)} \right)$
(11) end for
(12) return$\theta $,${\theta _v}$, $L\left( {p\|{s_j}} \right)$, $\zeta \left( {p\|{s_j}} \right)$
(13) 训练结束

下载: 导出CSV

算法2　结合基于时延的Dijkstra与DRL算法的SFC部署方法
输入：网络服务请求${s_i}$和网络状态信息；惩罚权重${\alpha _{{\rm{occupancy}}}}$, ${\alpha _{{\rm{bandwidth}}}}$；环境时延的相关参数
输出：SFC的部署策略${p^{{s_i}}}$
DDRL网络服务请求部署过程：
(1) 初始化放置序列$p \leftarrow \varnothing $，时延奖励$L\left( {p\|s} \right) \leftarrow \varnothing $，惩罚值$\zeta \left( {p\|s} \right) \leftarrow \varnothing $，拉格朗日值$G\left( {p\|s} \right) \leftarrow \varnothing $以及2个约束${\alpha _{{\mathrm{occupancy}}}} \leftarrow \varnothing $, 　${\alpha _{{\rm{bandwidth}}}} \leftarrow \varnothing $
(2) 遍历每个网络模型for m in range(models)：
(3) 　　加载模型m的参数$ \theta $,${\theta _v}$
(4) 　　for batch in range(128):
(5) 　　　　生成第batch条SFC的贪婪放置序列$p$, ${\text{l\_m}}[{\text{batch}}] \leftarrow G\left( {p\|s} \right)$
(6) 　　　　for sample in range(${\text{temp\_sample}}$):
(7) 　　　　　　通过温度超参数$T$控制输出分布的稀疏性，生成稀疏的放置序列${\text{p\_temp}}$
(8) 　　　　　　${\text{l\_m\_temp[sample][batch]}} \leftarrow G({\text{p\_temp}}\|s)$
(9) 　　　　取$G({\text{p\_temp}}\|s)$最小的放置序列作为第m个网络模型的温度抽样放置序列${\text{p\_m\_temp}}$
(10) 　　　生成贪婪放置${\text{p\_m}}$对应的拉格朗日值序列${\text{l\_m}}$, ${\text{l\_m\_temp}}$与惩罚值序列${\text{penalty\_m}}$, ${\text{penalty\_m\_temp}}$
(11)　　　取两种搜索算法的最小惩罚值，对应的放置序列为最优放置决策$p$
(12)　　　 end for
(13) return ${\mathrm{placement}}$, $L\left( {p\|s} \right)$,$\zeta \left( {p\|s} \right)$
(14) 部署结束

下载: 导出CSV

表 1 VNF的主要参数

VNF类型	所需CPU资源量	所需带宽	处理数据所消耗时延(ms)
1	4	10	10
2	3	8	8
3	2	6	6
4	1	2	2

下载: 导出CSV

参考文献(18)

[1]	陈卓, 冯钢, 刘怡静, 等. MEC中基于改进遗传模拟退火算法的虚拟网络功能部署策略[J]. 通信学报, 2020, 41(4): 70–80. doi: 10.11959/j.issn.1000-436x.2020074. CHEN Zhuo, FENG Gang, LIU Yijing, et al. Virtual network function deployment strategy based on improved genetic simulated annealing algorithm in MEC[J]. Journal on Communications, 2020, 41(4): 70–80. doi: 10.11959/j.issn.1000-436x.2020074.
[2]	ALLAHVIRDI A, YOUSEFI S, and SARDROUD A A. Placement of dynamic service function chains in partially VNF-enabled networks[J]. Telecommunication Systems, 2022, 81(2): 225–240. doi: 10.1007/s11235-022-00939-6.
[3]	YANG Song, LI Fan, YAHYAPOUR R, et al. Delay-sensitive and availability-aware virtual network function scheduling for NFV[J]. IEEE Transactions on Services Computing, 2022, 15(1): 188–201. doi: 10.1109/TSC.2019.2927339.
[4]	YAGHOUBPOUR F, BAKHSHI B, and SEIFI F. End-to-end delay guaranteed Service Function Chain deployment: A multi-level mapping approach[J]. Computer Communications, 2022, 194: 433–445. doi: 10.1016/j.comcom.2022.08.005.
[5]	唐伦, 李师锐, 杜雨聪, 等. 基于多智能体柔性演员-评论家学习的服务功能链部署算法[J]. 电子与信息学报, 2022, 45(8): 2893–2901. doi: 10.11999/JEIT220803. TANG Lun, LI Shirui, DU Yucong, et al. Deployment algorithm of service function chain based on multi-agent soft actor-critic learning[J]. Journal of Electronics & Information Technology, 2022, 45(8): 2893–2901. doi: 10.11999/JEIT220803.
[6]	LIU Hongtai, DING Shengduo, WANG Shunyi, et al. Multi-objective optimization service function chain placement algorithm based on reinforcement learning[J]. Journal of Network and Systems Management, 2022, 30(4): 58. doi: 10.1007/s10922-022-09673-5.
[7]	徐泽汐, 庄雷, 张坤丽, 等. 基于知识图谱的服务功能链在线部署算法[J]. 通信学报, 2022, 43(8): 41–51. doi: 10.11959/j.issn.1000-436x.2022154. XU Zexi, ZHUANG Lei, ZHANG Kunli, et al. Online placement algorithm of service function chain based on knowledge graph[J]. Journal on Communications, 2022, 43(8): 41–51. doi: 10.11959/j.issn.1000-436x.2022154.
[8]	HU Haiyan, KANG Qiaoyan, ZHAO Shuo, et al. Service function chain deployment method based on traffic prediction and adaptive virtual network function scaling[J]. Electronics, 2022, 11(16): 2625. doi: 10.3390/electronics11162625.
[9]	YALA L, FRANGOUDIS P A, and KSENTINI A. Latency and availability driven VNF placement in a MEC-NFV environment[C]. 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 2018: 1–7. doi: 10.1109/GLOCOM.2018.8647858.
[10]	石尚. 蜂窝移动网络下服务功能链的部署与动态配置研究[D]. [硕士论文], 北京邮电大学, 2021. doi: 10.26969/d.cnki.gbydu.2021.002972. SHI Shang. Research on deployment and dynamic configuration of service function chain in mobile cellular network[D]. [Master dissertation], Beijing University of Posts and Telecommunications, 2021. doi: 10.26969/d.cnki.gbydu.2021.002972.
[11]	NAM Y, SONG S, and CHUNG J M. Clustered NFV Service chaining optimization in mobile edge clouds[J]. IEEE Communications Letters, 2017, 21(2): 350–353. doi: 10.1109/LCOMM.2016.2618788.
[12]	ADDIS B, BELABED D, BOUET M, et al. Virtual network functions placement and routing optimization[C]. 2015 IEEE 4th International Conference on Cloud Networking (CloudNet), Niagara Falls, Canada, 2015: 171–177. doi: 10.1109/CloudNet.2015.7335301.
[13]	MIJUMBI R, SERRAT J, GORRICHO J L, et al. Design and evaluation of algorithms for mapping and scheduling of virtual network functions[C]. The 2015 1st IEEE Conference on Network Softwarization (NetSoft), London, UK, 2015: 1–9. doi: 10.1109/NETSOFT.2015.7116120.
[14]	TESSLER C, MANKOWITZ J D, and MANNOR S. Reward constrained policy optimization[C]. International Conference on Learning Representations, New Orleans, USA, 2019. doi: 10.48550/arXiv.1805.11074.
[15]	MIJUMBI R, SERRAT J, GORRICHO J, et al. Network function virtualization: State-of-the-art and research challenges[J]. IEEE Communications Surveys & Tutorials, 2016, 18(1): 236–262. doi: 10.1109/COMST.2015.2477041.
[16]	ZHANG Yuchao, XU Ke, WANG Haiyang, et al. Going fast and fair: Latency optimization for cloud-based service chains[J]. IEEE Network, 2018, 32(2): 138–143. doi: 10.1109/MNET.2017.1700275.
[17]	WILLIAMS R. J. Simple statistical gradient-following algorithms for connectionist reinforcement learning[J]. Machine Learning, 1992, 8(3/4): 229–256. doi: 10.1007/BF00992696.
[18]	SUTTON R S and BARTO A G. Reinforcement Learning: An Introduction[M]. Cambridge, USA: MIT Press, 1998: 229–235.