Downlink Transmission for RIS-Assisted MIMO NOMA by Exploiting Statistical CSI
-
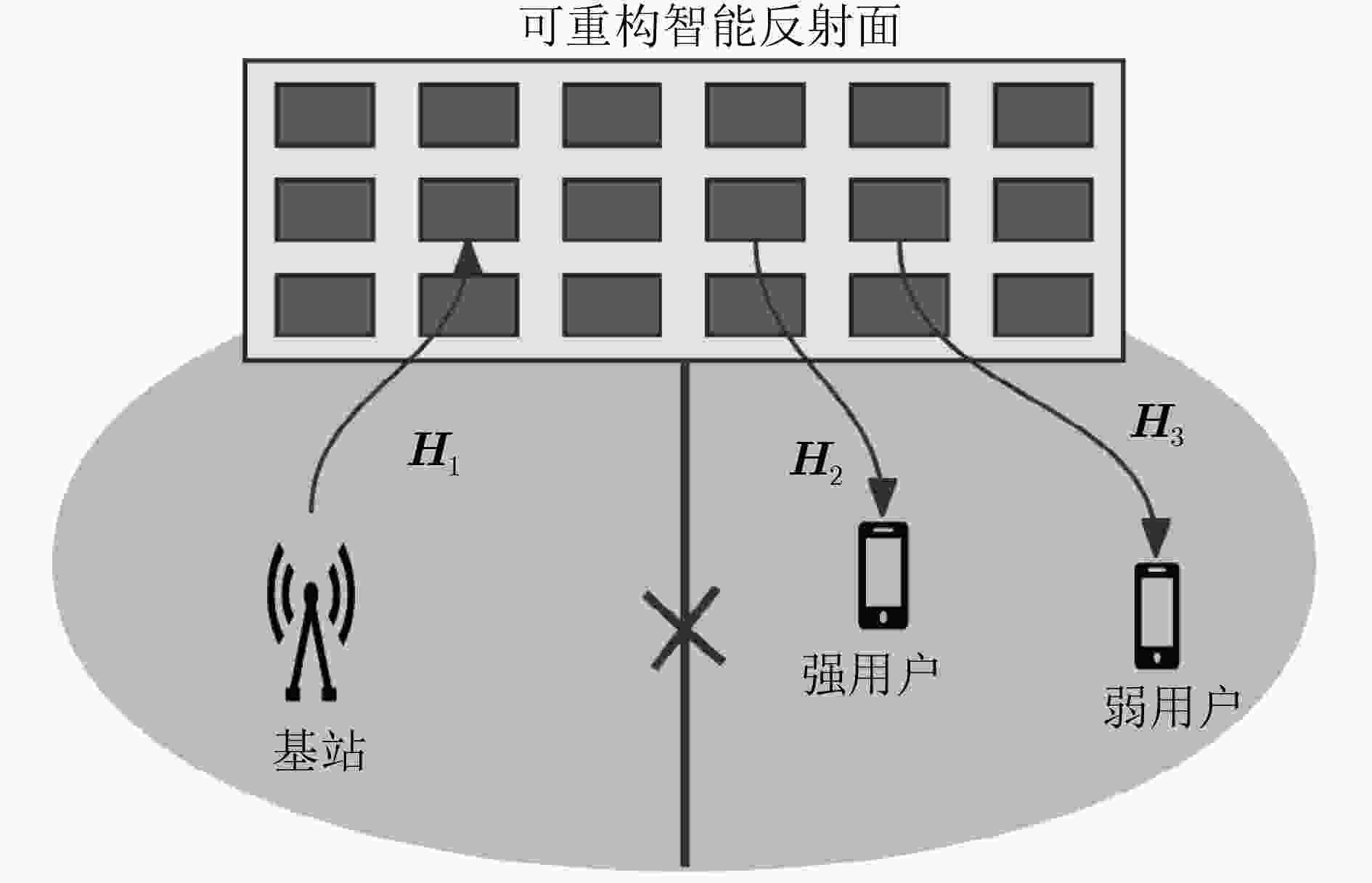
摘要: 针对可重构智能反射表面(RIS)辅助多输入多输出(MIMO)非正交多址接入(NOMA)下行传输系统,该文提出利用统计信道状态信息(CSI)的基站发送协方差矩阵与RIS相移矩阵设计方法。首先,在莱斯空间相关信道假设下,利用大维随机矩阵理论,推导了RIS辅助MIMO NOMA系统遍历和速率的确定性表达式;然后,在弱用户速率约束与发送功率受限的条件下,通过最大化确定性大系统近似和速率,利用统计CSI,分别设计了强、弱用户的次优发送协方差矩阵和RIS的相移矩阵。仿真结果表明,所推导的近似表达式具有很好的近似效果,所设计的发送协方差矩阵和相移矩阵能显著提升系统的和速率。Abstract: For a Reconfigurable Intelligent Surface (RIS)-assisted Multiple Input Multiple Output (MIMO) Non-Orthogonal Multiple Access (NOMA) downlink system, the transmit covariances matrix at the base station and the phase-shifting matrix at the RIS are jointly designed based on statistical Channel State Information (CSI). First, in the spatial correlated Rician channel, a deterministic large-system approximation for the ergodic sum rate is obtained for an RIS-assisted MIMO-NOMA system by resorting to the large-dimensional random matrix theory. Then, by maximizing the approximated sum rate, the transmit covariances matrix for the strong and weak user as well as the phase-shifting matrix at the RIS are designed based on statistical CSI under the constraints of total transmit power and the rates threshold for weak user. The simulations validate the high accuracy of our approximations and our proposed transmit covariances and phase-shifting matrix can improve the system performances significantly.
-
1 交替优化算法
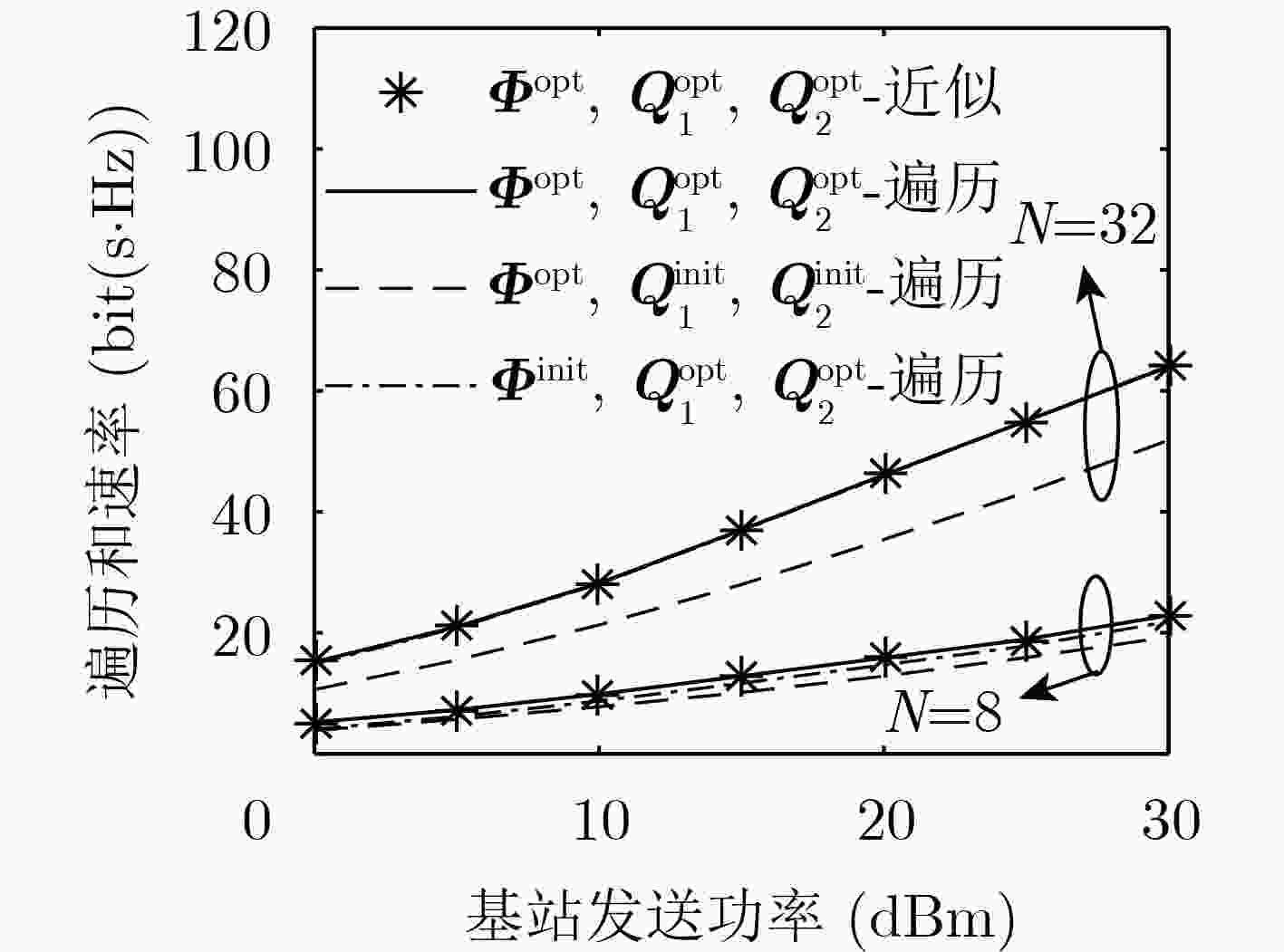
(1) 初始化:${\boldsymbol{Q}}_1^{(0)} = {{\boldsymbol{I}}_N},{\boldsymbol{\tilde Q}}_1^{(0)} = { {\textit{0}}},{\boldsymbol{Q}}_2^{(0)} = {{\boldsymbol{I}}_N},P_1^{(0)} = 0.5$,
${{\boldsymbol{\varPhi }}^{(0)}} = {{\boldsymbol{\varPhi }}^{{\text{rand}}}},\varepsilon = {10^{ - 5}},t = 0 $;(2) 步骤1 给定${\boldsymbol{\varPhi }}$,求解${\boldsymbol{Q}}_1^{{\text{opt}}}$, ${\boldsymbol{Q}}_2^{{\text{opt}}}$; (a) 根据${\boldsymbol{Q}}_1^{(t - 1)}$和$P_1^{(t - 1)}$,求解问题$({\text{P}}3)$得到${\boldsymbol{Q}}_2^{(t)}$; (b) 根据${\boldsymbol{\tilde Q}}_1^{(t - 1)}$, ${\boldsymbol{Q}}_2^{(t)}$和$P_1^{(t - 1)}$,求解问题$({\text{P}}4)$得到${\boldsymbol{Q}}_1^{(t)}$; (c) 记${\boldsymbol{Q}}_1^{{\text{opt}}} = {\boldsymbol{Q}}_1^{(t)}$, ${\boldsymbol{Q}}_2^{{\text{opt}}} = {\boldsymbol{Q}}_2^{(t)}$; (3) 步骤2 给定${{\boldsymbol{Q}}_1}$, ${{\boldsymbol{Q}}_2}$,求解${{\boldsymbol{\varPhi }}^{{\text{opt}}}}$; (a) 由${{\boldsymbol{\varPhi }}^{\left( {t - 1} \right)}}$以及式(35)计算${\nabla _{\boldsymbol{\theta}} }{\bar R^{(t - 1)}}_{{\text{sum}}}$; (b) 由式(37)计算${{\boldsymbol{\theta }}^{(t)}}$,得${{\boldsymbol{\varPhi }}^{(t)}} = {\text{diag(}}{{\boldsymbol{\theta }}^{(t)}}{\text{)}}$ (c) 更新$t = t + 1$; (d) 循环步骤2直至速率增量满足$\left| \bar R_{{\text{sum}}}^{(t + 1)} - \bar R_{{\text{sum}}}^{(t)} \right| < \varepsilon $; (e) 记${{\boldsymbol{\varPhi }}^{{\text{opt}}}} = {{\boldsymbol{\varPhi }}^{\left( t \right)}}$; (f) 根据${\boldsymbol{Q}}_1^{(t)}$, ${\boldsymbol{Q}}_2^{(t)}$和${{\boldsymbol{\varPhi }}^{\left( t \right)}}$,求解问题$({\text{P8}})$得到功率分配因子
$P_1^{(t)}$;(g) 记${\boldsymbol{Q}}_1^{{\text{opt}}} = P_1^{(t)}{\boldsymbol{Q}}_1^{{\text{opt}}}$和${\boldsymbol{Q}}_2^{{\text{opt}}} = (P - P_1^{(t)}){\boldsymbol{Q}}_2^{{\text{opt}}}$; (4) 循环步骤1~2直至${\bar R_{{\text{sum}}}}$增量小于$\varepsilon $; (5) 输出${\boldsymbol{Q}}_1^{{\text{opt}}}$, ${\boldsymbol{Q}}_2^{{\text{opt}}}$和${{\boldsymbol{\varPhi }}^{{\text{opt}}}}$。 表 1 默认仿真参数设置
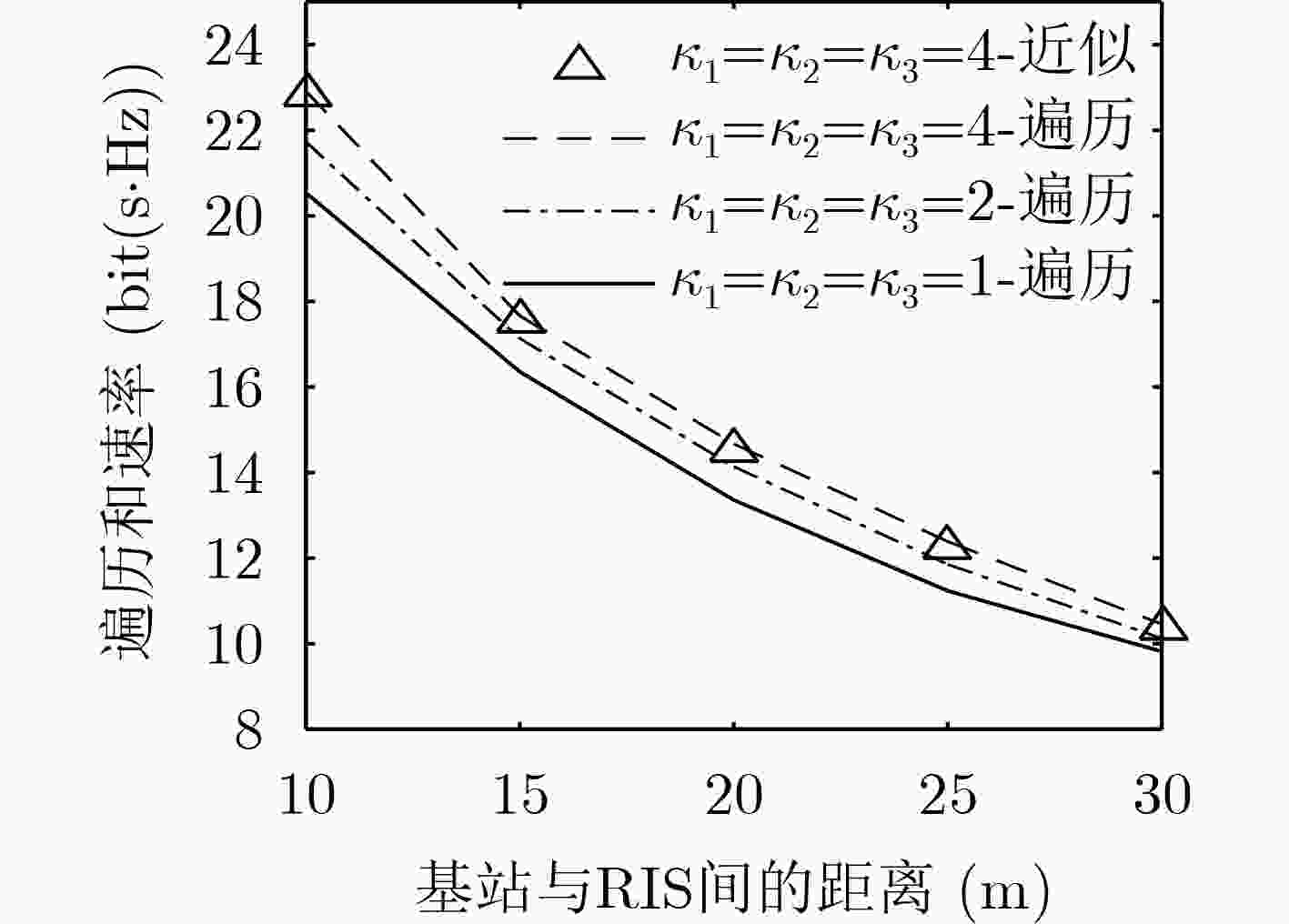
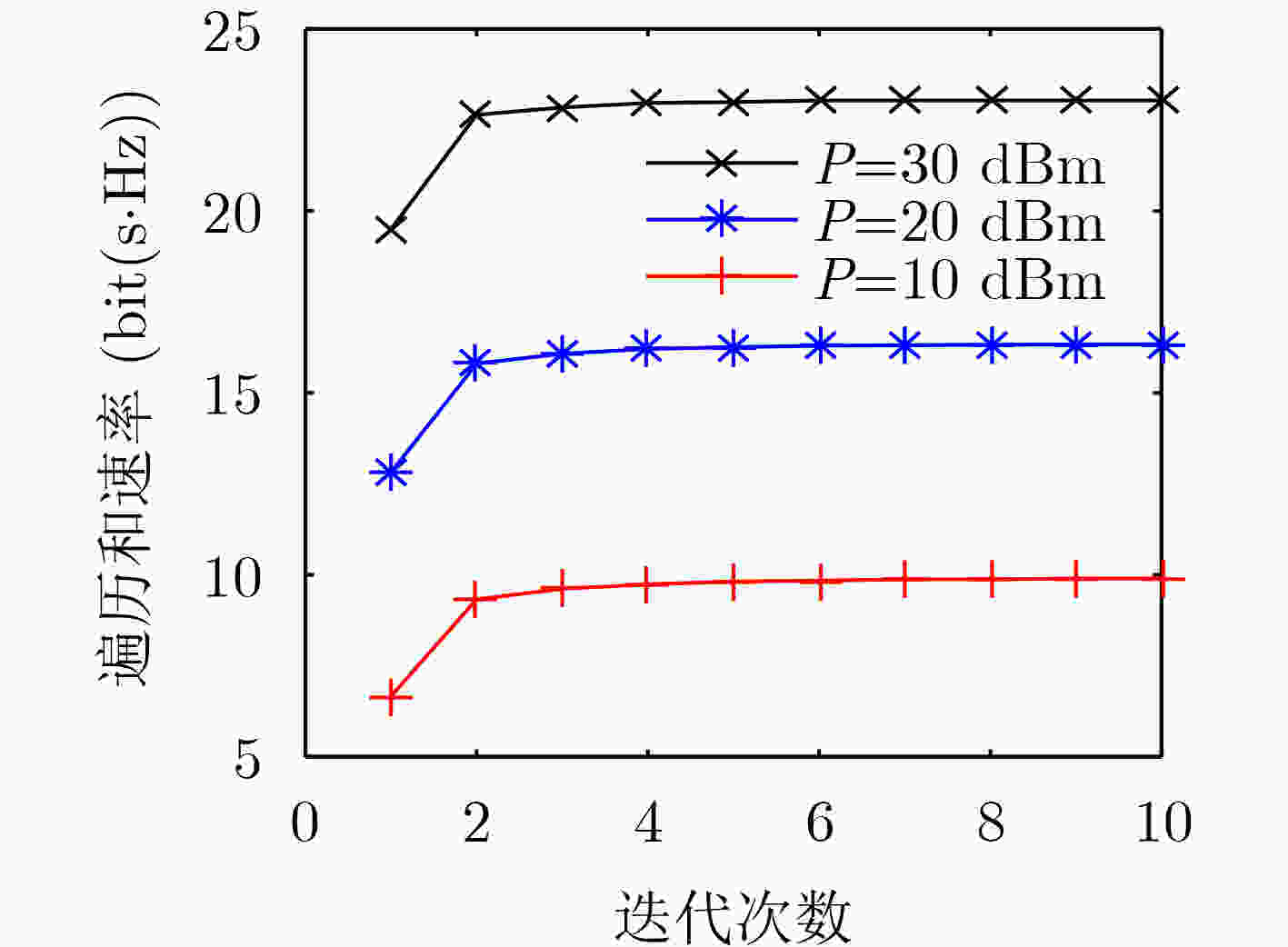
总功率$ P $ 噪声功率 弱用户速率需求$ {R_0} $ 角度拓展$ {\delta _i} $ 平均角度 试验次数 30 dBm –80 dBm 1.5 bps/Hz $ {10^ \circ } $ $ \begin{gathered} {\theta _{{T_1}}} = {\theta _{{T_2}}} = {0^ \circ },{\theta _{{T_3}}} = {10^ \circ } \\ {\theta _{{R_1}}} = {\theta _{{R_2}}} = - {5^ \circ },{\theta _{{R_3}}} = {5^ \circ } \\ \end{gathered} $ $ {10^4} $ -
[1] YOU Xiaohu, WANG Chengxiang, HUANG Jie, et al. Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts[J]. Science China Information Sciences, 2021, 64(1): 110301. doi: 10.1007/s11432-020-2955-6. [2] 钱志鸿, 肖琳, 王雪. 面向未来移动网络密集连接的关键技术综述[J]. 通信学报, 2021, 42(4): 22–43. doi: 10.11959/j.issn.1000-436x.2021094.QIAN Zhihong, XIAO Lin, and WANG Xue. Review on strategic technology of dense connection for the future mobile network[J]. Journal on Communications, 2021, 42(4): 22–43. doi: 10.11959/j.issn.1000-436x.2021094. [3] 刘期烈, 辛雅楠, 高俊鹏, 等. 可重构智能表面辅助的非正交多址接入网络鲁棒能量效率资源分配算法[J]. 电子与信息学报, 2022, 44(7): 2332–2341. doi: 10.11999/JEIT210521.LIU Qilie, XIN Yanan, GAO Junpeng, et al. Robust energy efficiency resource allocation algorithm in reconfigurable intelligent surface-assisted non-orthogonal multiple access networks[J]. Journal of Electronics & Information Technology, 2022, 44(7): 2332–2341. doi: 10.11999/JEIT210521. [4] ZHANG Shuhang, ZHANG Hongliang, DI Boya, et al. Intelligent omni-surfaces: Ubiquitous wireless transmission by reflective-refractive metasurfaces[J]. IEEE Transactions on Wireless Communications, 2022, 21(1): 219–233. doi: 10.1109/TWC.2021.3094869. [5] ZUO Jiakuo, LIU Yuanwei, QIN Zhijin, et al. Resource allocation in intelligent reflecting surface assisted NOMA systems[J]. IEEE Transactions on Communications, 2020, 68(11): 7170–7183. doi: 10.1109/TCOMM.2020.3016742. [6] ZUO Jiakuo, LIU Yuanwei, BASAR E, et al. Intelligent reflecting surface enhanced millimeter-wave NOMA systems[J]. IEEE Communications Letters, 2020, 24(11): 2632–2636. doi: 10.1109/LCOMM.2020.3009158. [7] CHEN Jiagao and YU Xiangbin. Ergodic rate analysis and phase design of STAR-RIS aided NOMA with statistical CSI[J]. IEEE Communications Letters, 2022, 26(12): 2889–2893. doi: 10.1109/LCOMM.2022.3202346. [8] WU Chenyu, SHI Shuo, YOU Changsheng, et al. STAR-RIS aided NOMA communication system with statistical CSI[C]. 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 2022: 100–105. doi: 10.1109/GCWkshps56602.2022.10008705. [9] ZHANG Zhen, CHEN Jian, LIU Yuanwei, et al. On the secrecy design of STAR-RIS assisted uplink NOMA networks[J]. IEEE Transactions on Wireless Communications, 2022, 21(12): 11207–11221. doi: 10.1109/TWC.2022.3190563. [10] ZHANG Jun, LIU Jie, MA Shaodan, et al. Large system achievable rate analysis of RIS-assisted MIMO wireless communication with statistical CSIT[J]. IEEE Transactions on Wireless Communications, 2021, 20(9): 5572–5585. doi: 10.1109/TWC.2021.3068494. [11] SHIU D S, FOSCHINI G J, GANS M J, et al. Fading correlation and its effect on the capacity of multielement antenna systems[J]. IEEE Transactions on Communications, 2000, 48(3): 502–513. doi: 10.1109/26.837052. [12] ZHANG Jun, YUEN Chao, WEN Chaokai, et al. Large system secrecy rate analysis for SWIPT MIMO wiretap channels[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(1): 74–85. doi: 10.1109/TIFS.2015.2477050. [13] ZHANG Jun, WEN Chaokai, JIN Shi, et al. On capacity of large-scale MIMO multiple access channels with distributed sets of correlated antennas[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(2): 133–148. doi: 10.1109/JSAC.2013.130203. [14] FAKOORIAN S A A and SWINDLEHURST A L. Optimal power allocation for GSVD-based beamforming in the MIMO Gaussian wiretap channel[C]. 2012 IEEE International Symposium on Information Theory Proceedings, Cambridge, USA, 2012: 2321–2325. doi: 10.1109/ISIT.2012.6283927. [15] NADEEM Q U A, KAMMOUN A, CHAABAN A, et al. Asymptotic max-min SINR analysis of reconfigurable intelligent surface assisted MISO systems[J]. IEEE Transactions on Wireless Communications, 2020, 19(12): 7748–7764. doi: 10.1109/TWC.2020.2986438. [16] MOUSTAKAS A L, SIMON S H, and SENGUPTA A M. MIMO capacity through correlated channels in the presence of correlated interferers and noise: A (not so) large N analysis[J]. IEEE Transactions on Information Theory, 2003, 49(10): 2545–2561. doi: 10.1109/TIT.2003.817427. -





 下载:
下载:
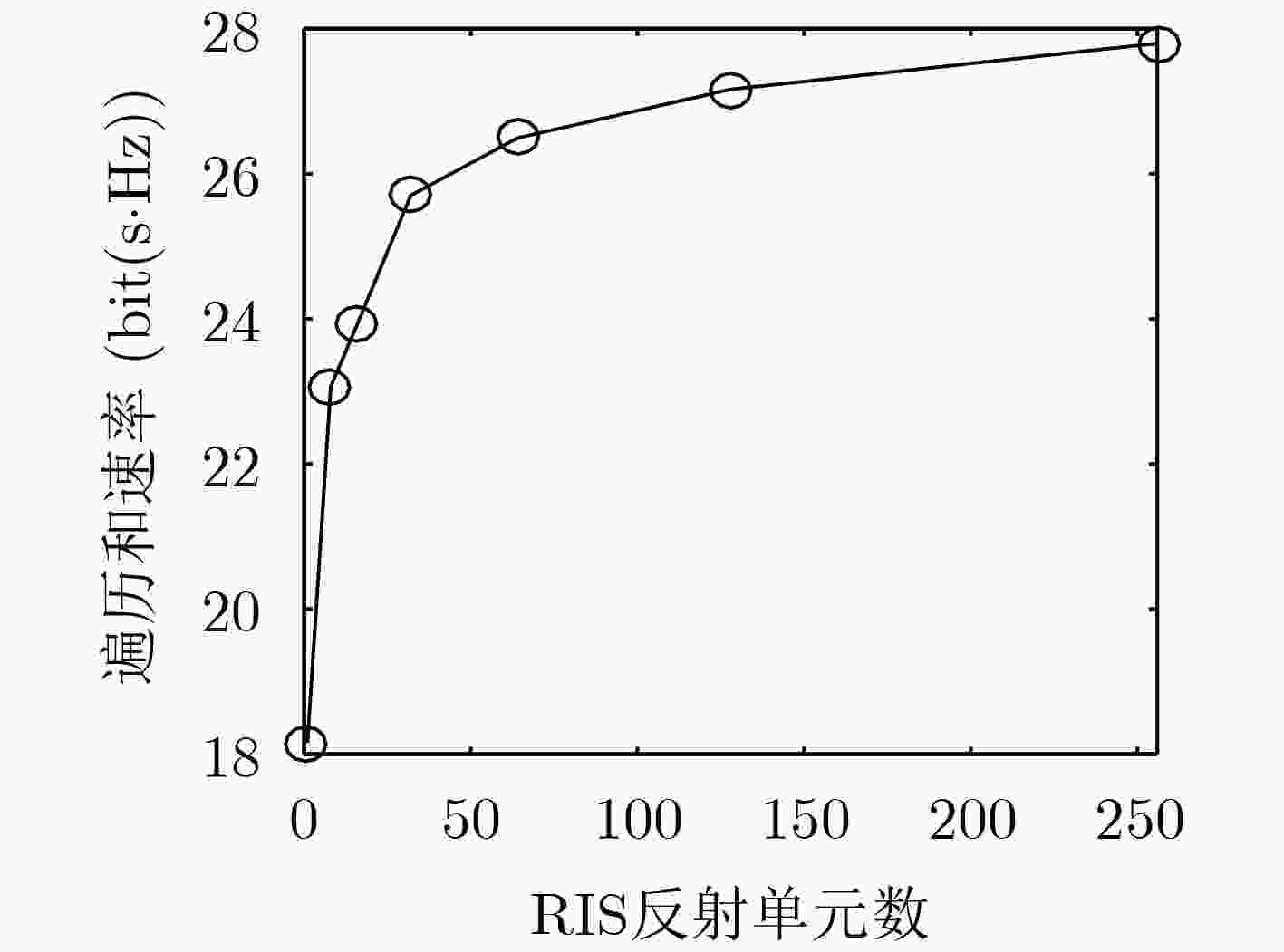
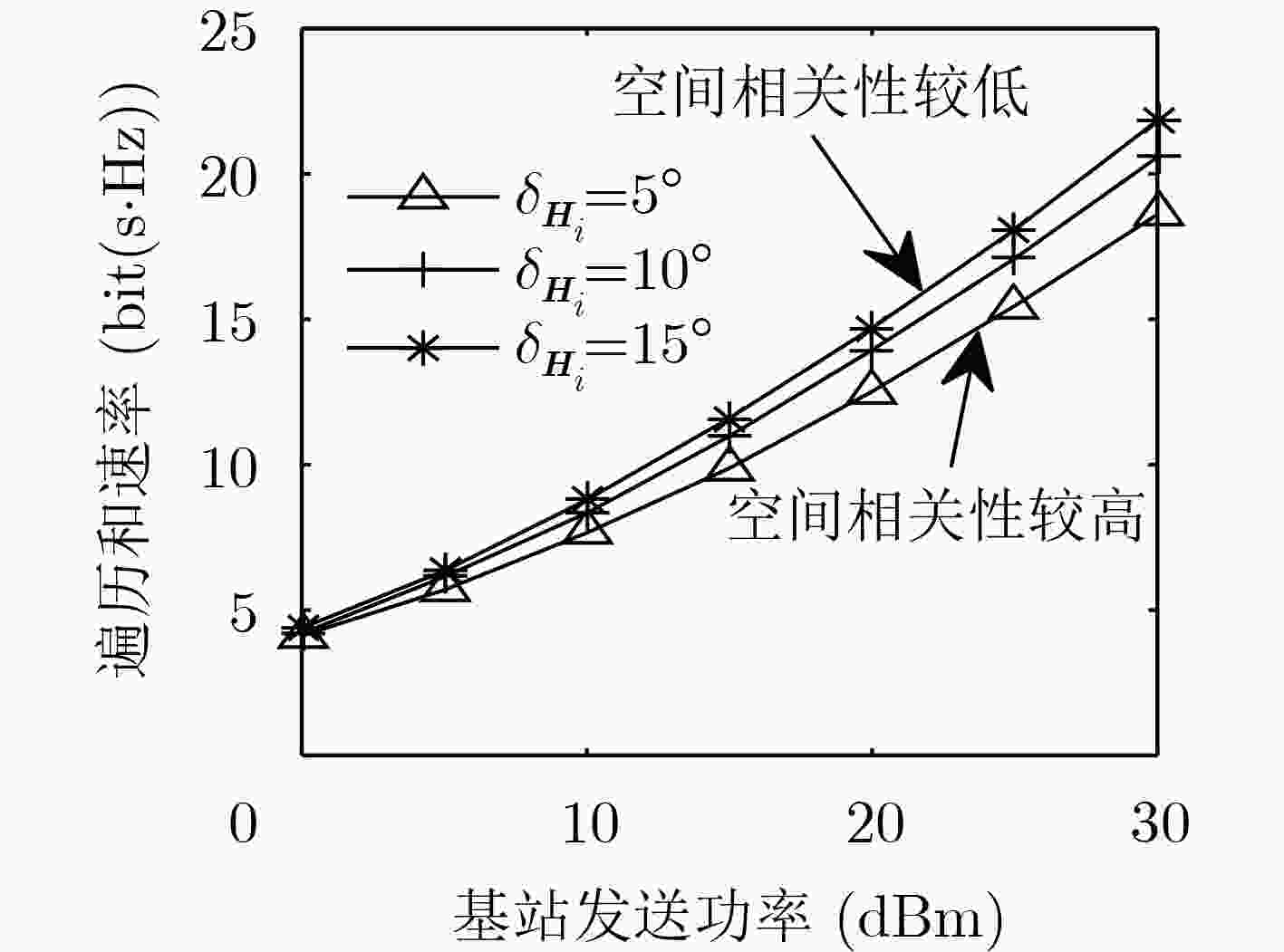


 下载:
下载:
