A Noise Subspace Projection Method Based on Spatial Transformation Preprocessing
-
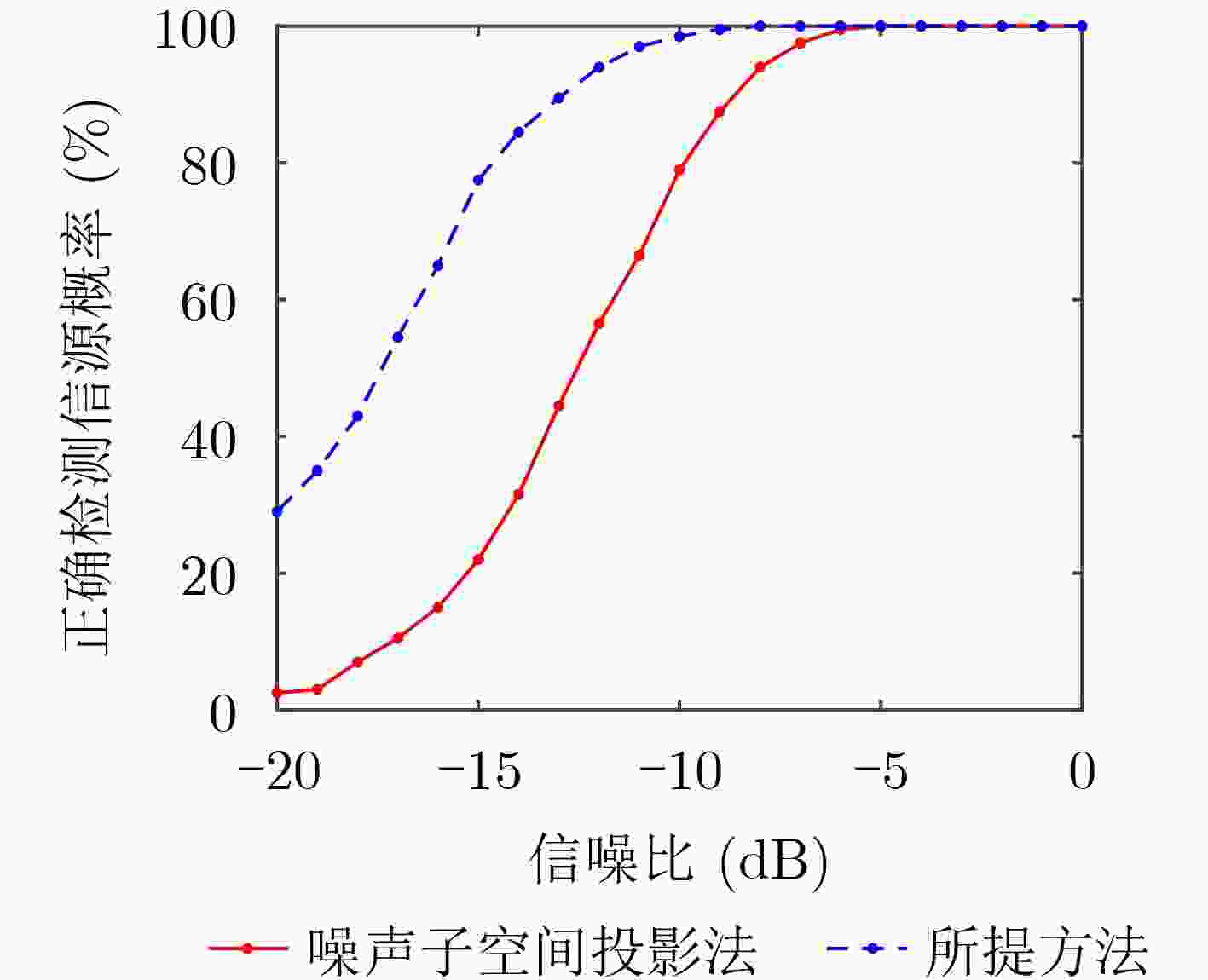
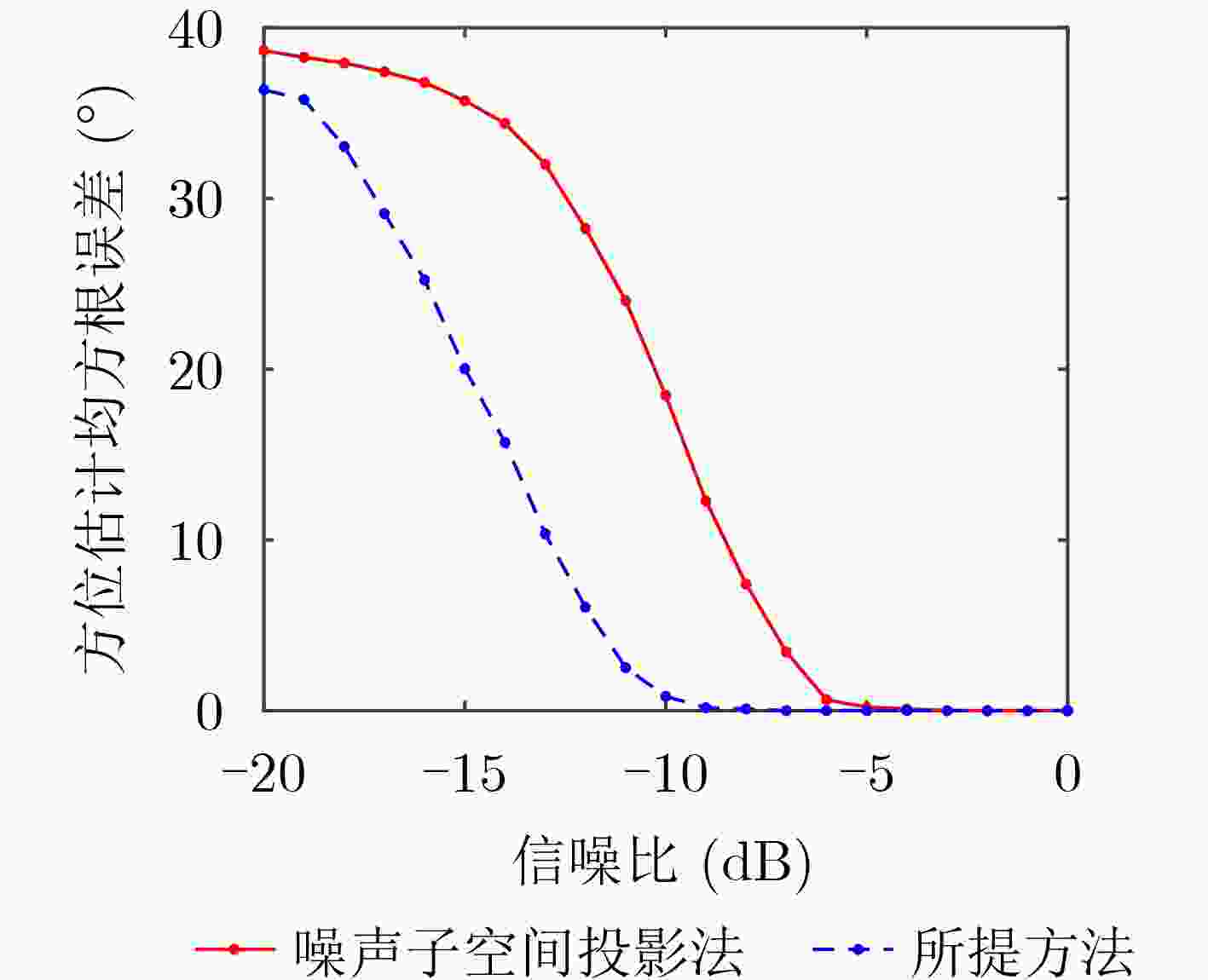
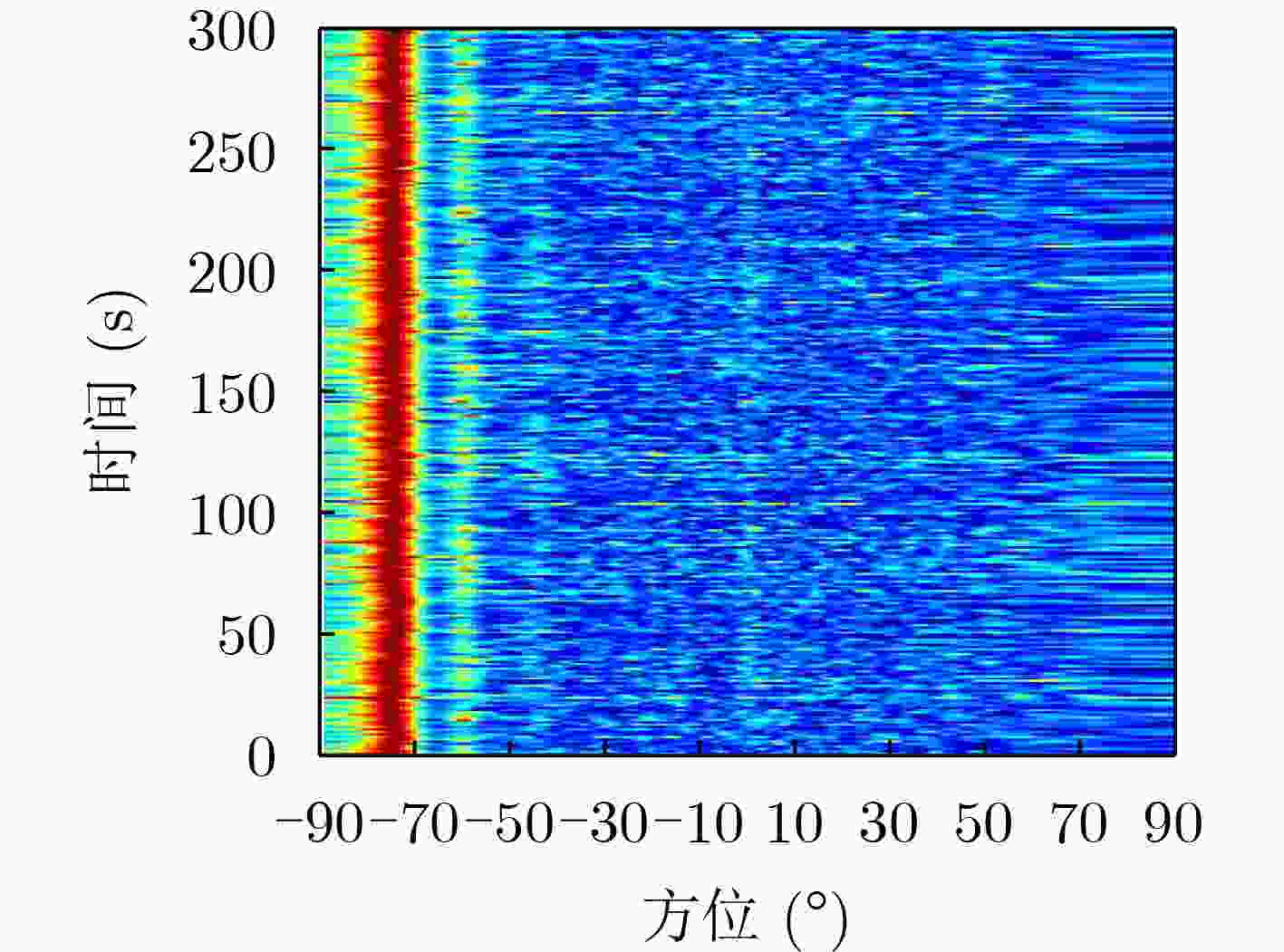
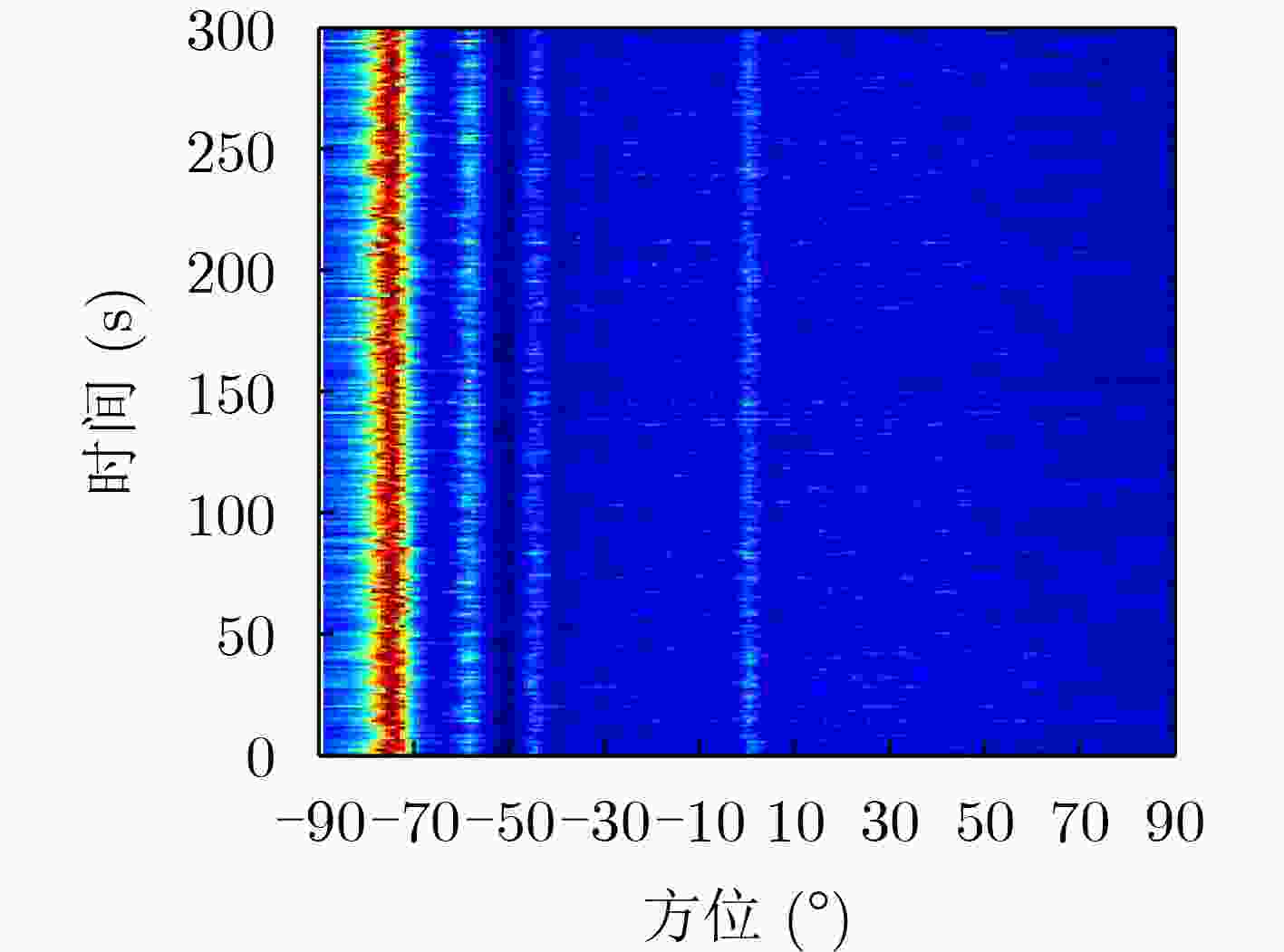
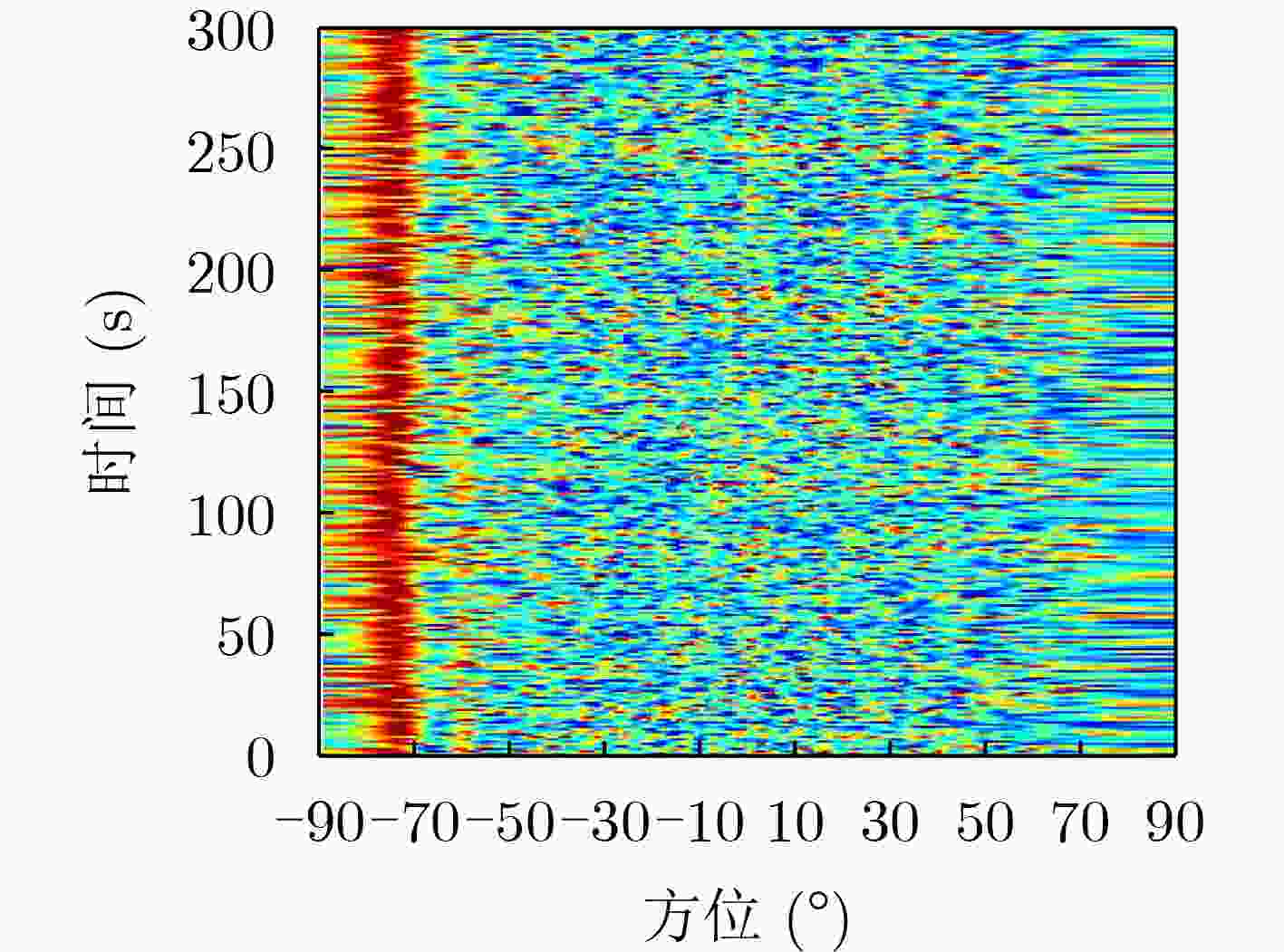
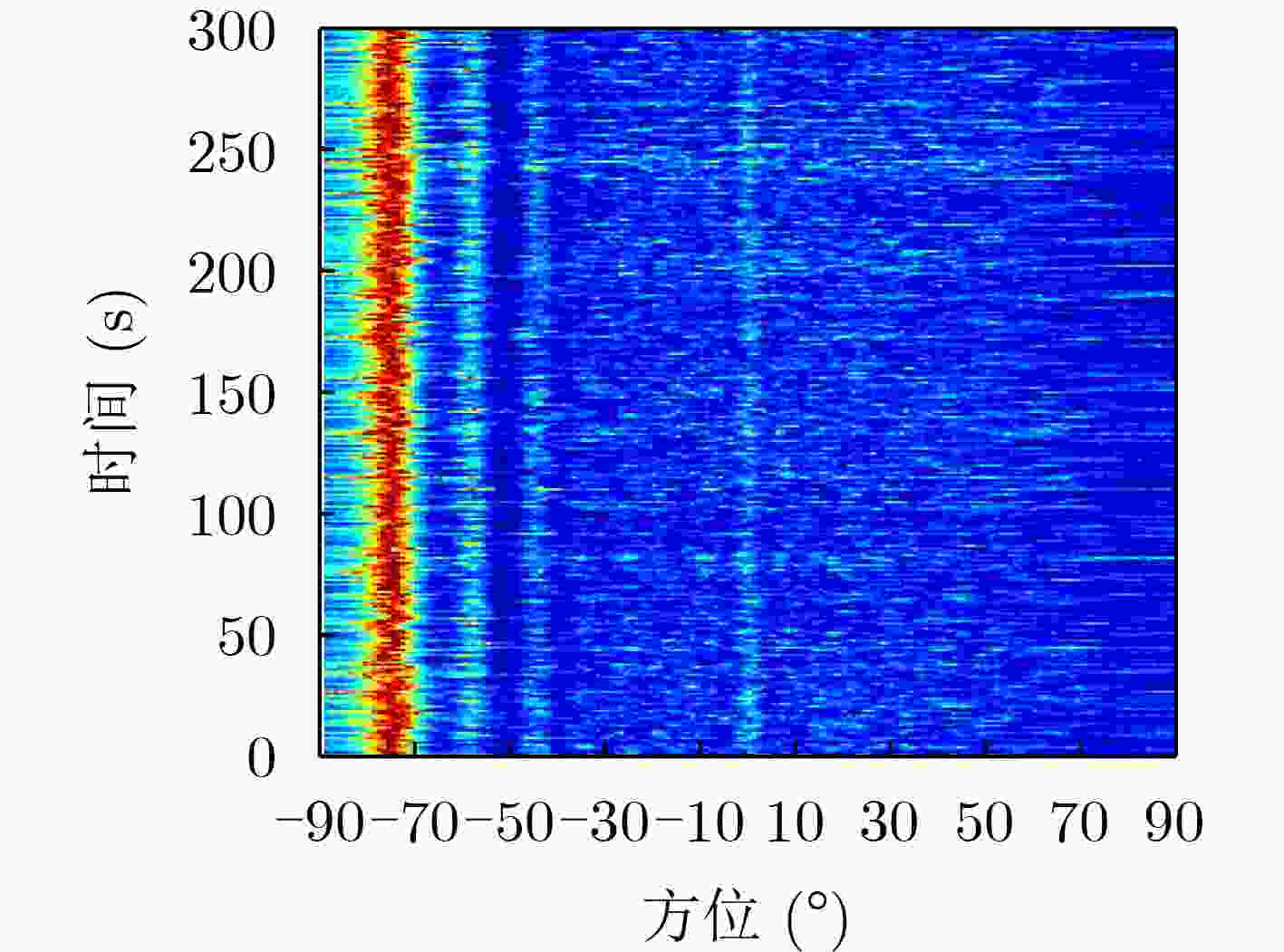
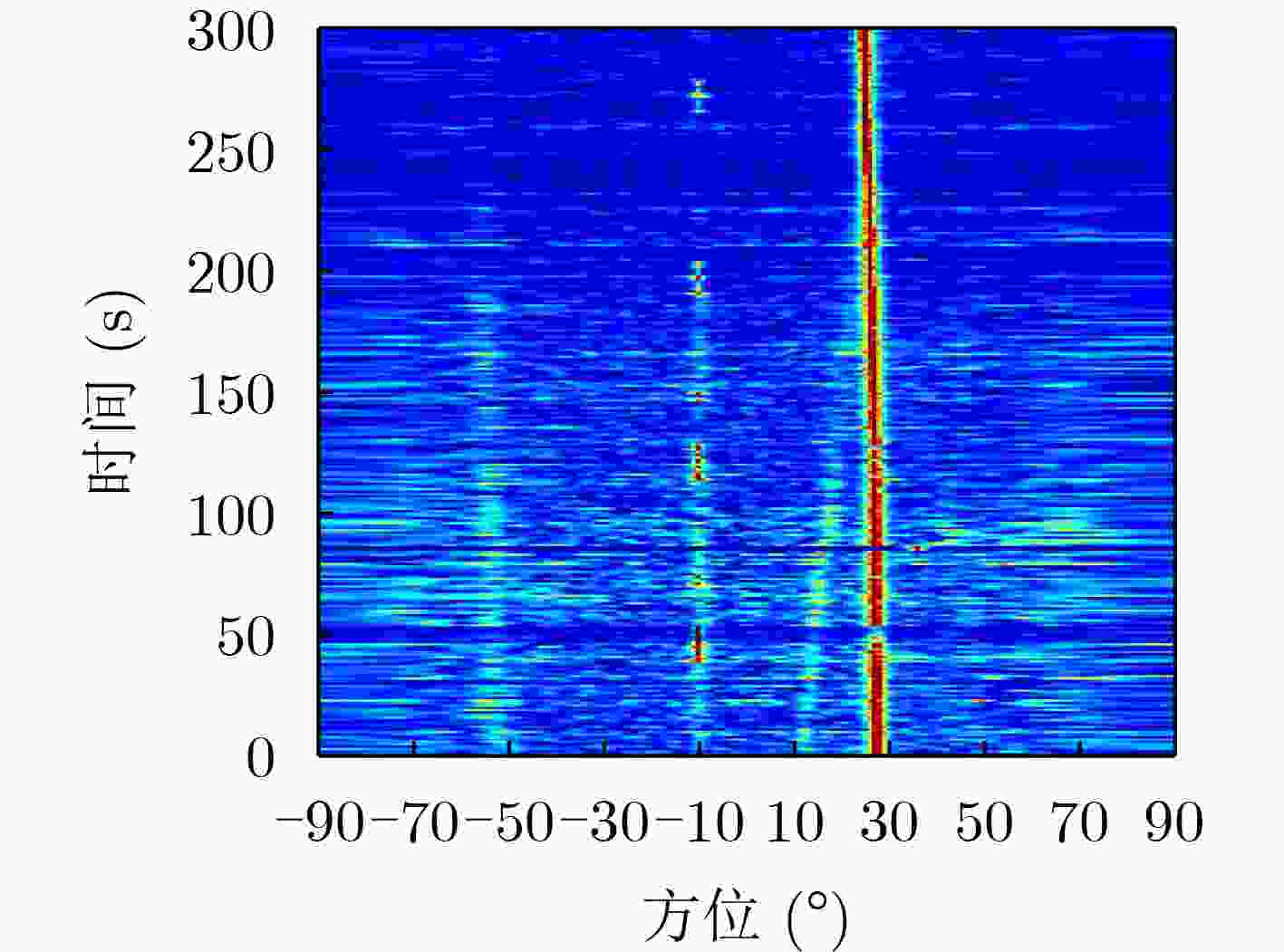
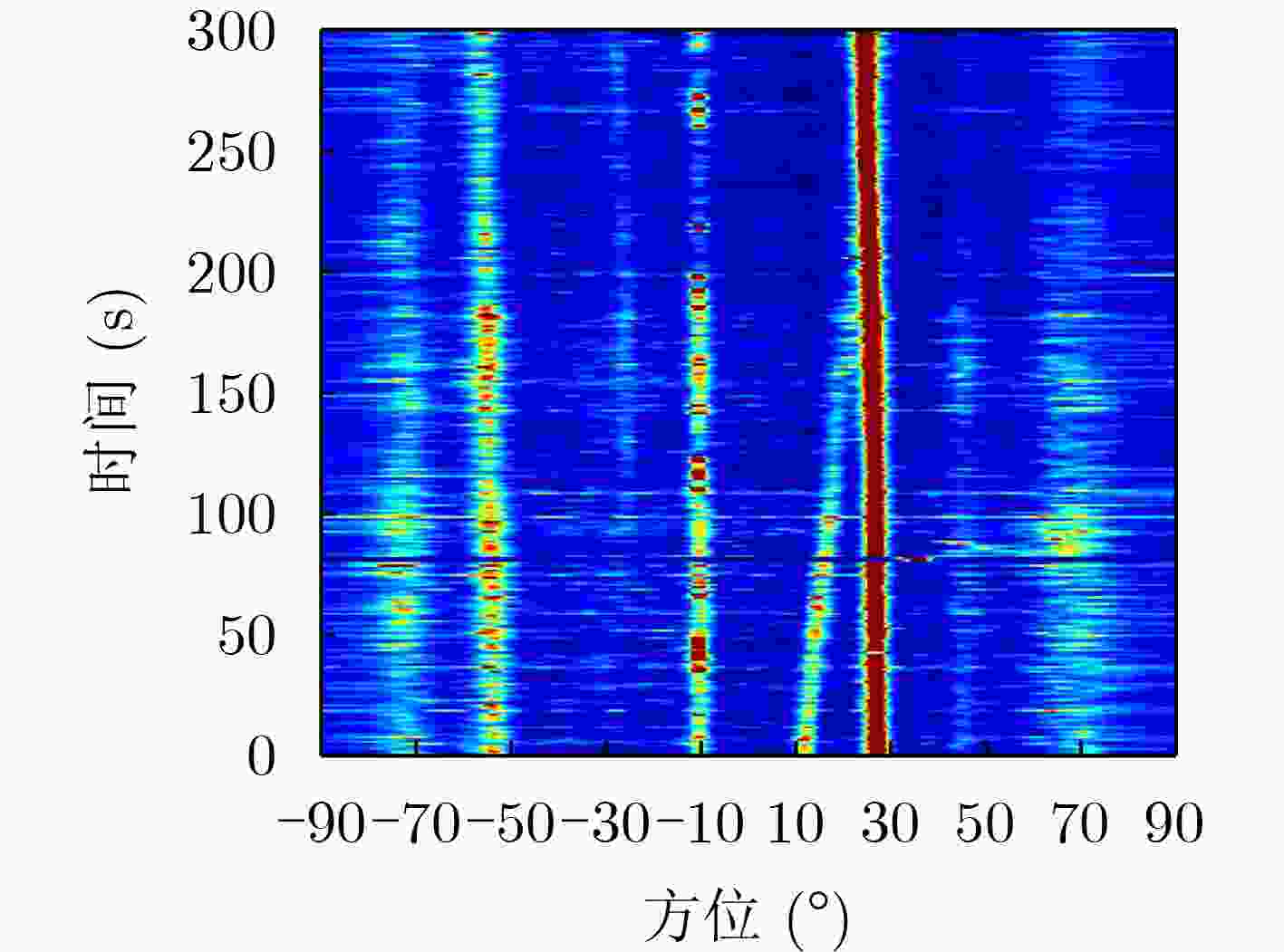
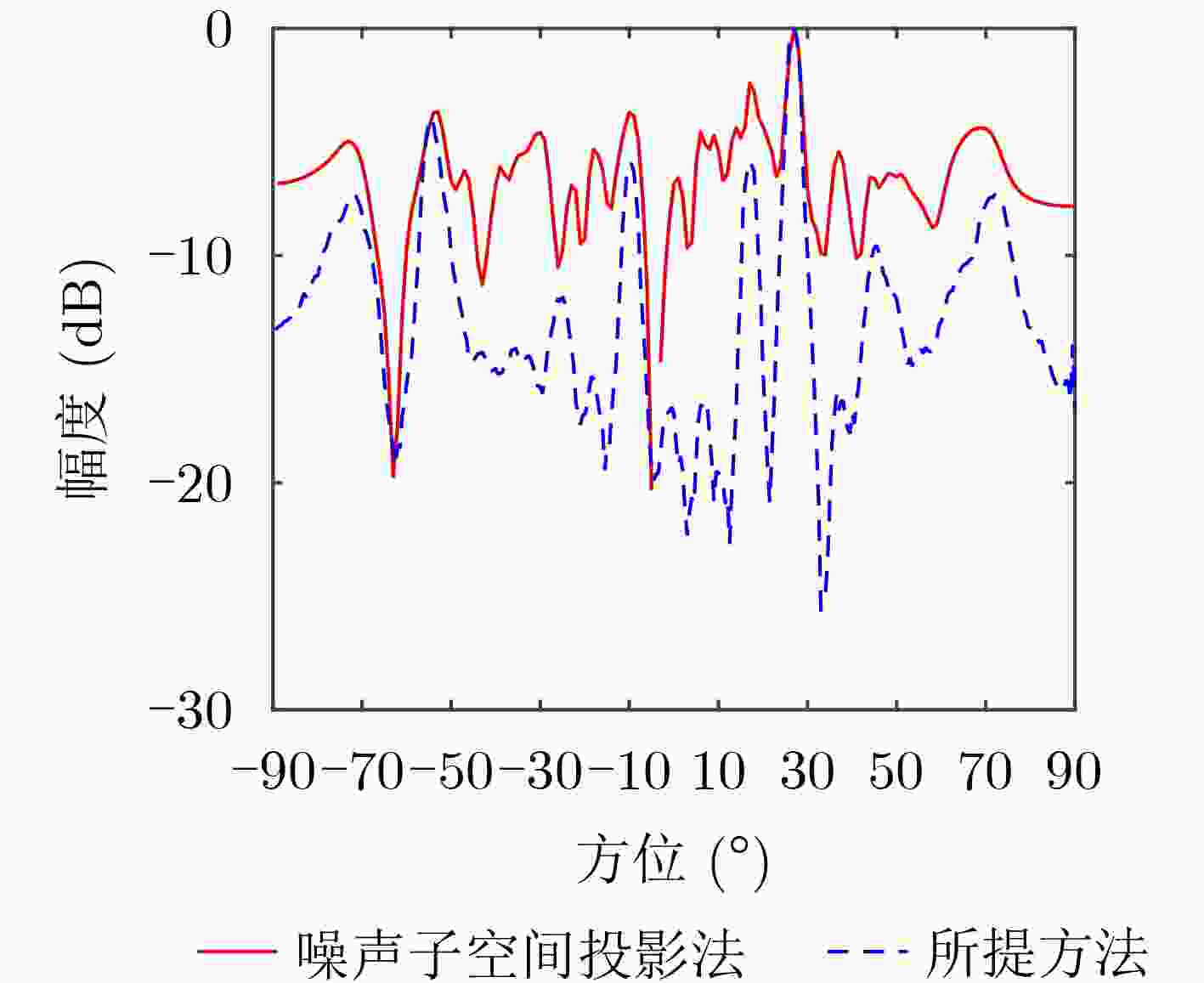
摘要: 针对基于噪声子空间投影的空间谱合成技术对输入信噪比(SNR)要求较高的问题,该文提出一种基于空间变换预处理的改进噪声子空间投影法。在子阵维度上,对阵列数据进行拆分处理,得到空间-空间-频率3维数据;利用空间投影变换,将其重新投影为空间-频率2维数据,实现子阵维度相干累积,提高空间变换后输入信噪比;采用噪声子空间投影法,对变换后数据进行处理,实现空间谱合成。数值仿真和实测数据处理结果表明:相比噪声子空间投影法,在保持方位分辨率不变的前提下,所提方法对输入信噪比的最低要求降低约6 dB,有效提升了噪声子空间投影法的弱信源检测性能。Abstract: To address the issue of high input Signal-to-Noise Ratio (SNR) in the spatial spectrum synthesis technique based on noise subspace projection, an improved noise subspace projection method based on spatial transformation preprocessing is proposed. First, the receiver array is uniformly split into sub-arrays to form three-dimensional space-space-frequency data. Then, three-dimensional data is projected into two-dimensional space-frequency data by spatial transformation, realizing coherent accumulation in the sub-array dimension and enhancing the input SNR after spatial transformation. Finally, the spatial spectrum synthesis is achieved by processing the two-dimensional transformed data, based on the noise subspace projection method. Numerical simulation and data processing results demonstrate that, compared with the noise subspace projection method, the proposed method decreases effectively the minimum input SNR by 6 dB while maintaining the bearing resolution, enhancing effectively the weak target detection performance of the noise subspace projection method.
-
表 1 数值仿真参数设置
参数类型 参数设置 阵型 水平线列阵 阵元数量M 32 阵元间距$ d $ 2 m 采样频率$ {f_s} $ 5 kHz 正横方位 0° 信源方位 $ {\theta _0} $ 中心频率$ {f_0} $ 375 Hz 表 2 2种方法对应空间谱对比度评价
方法 边缘锐度 背景级(dB) 噪声子空间投影法 0.69 –21.56 所提方法 0.98 –48.67 表 3 数据处理参数设置
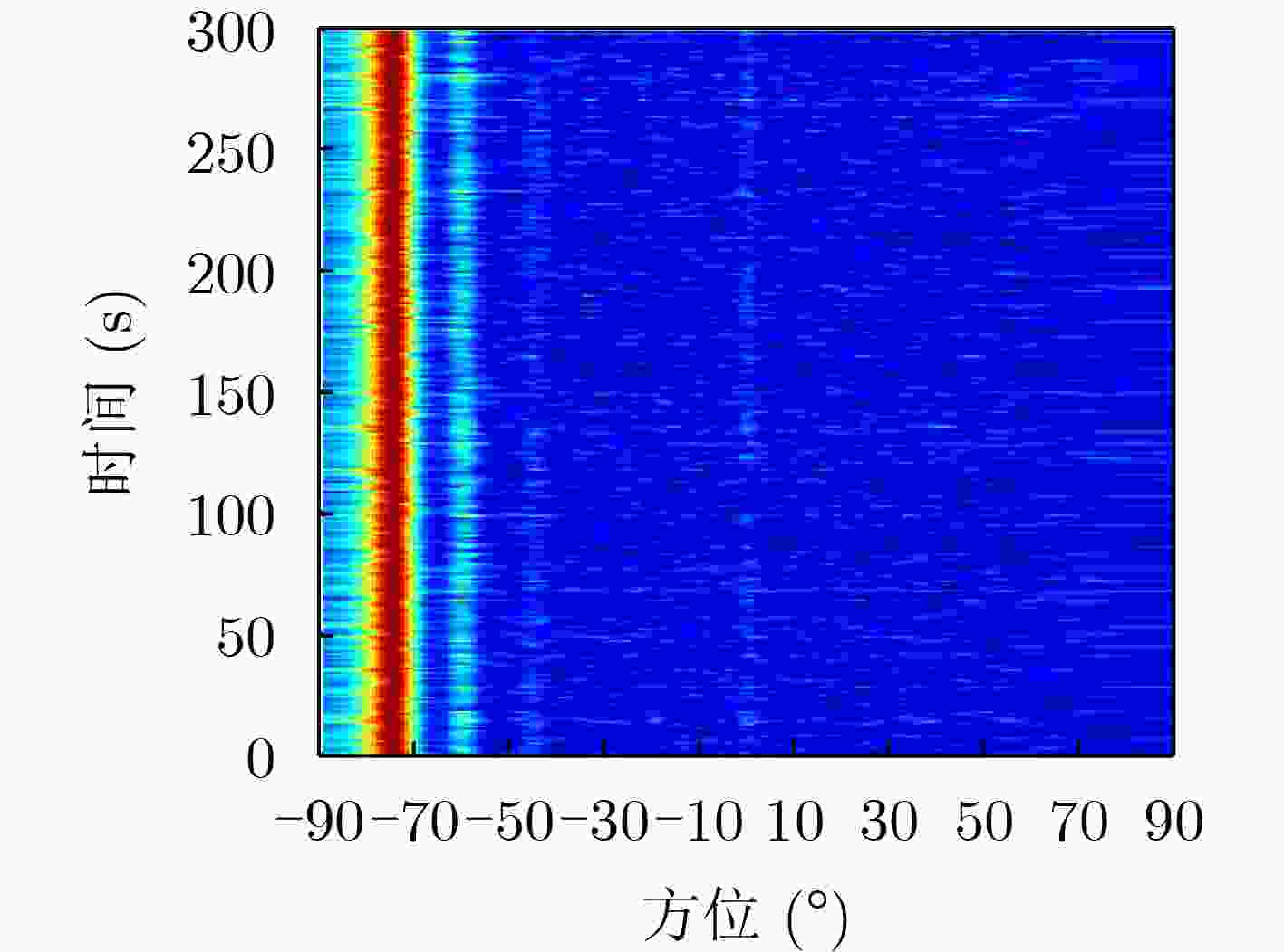
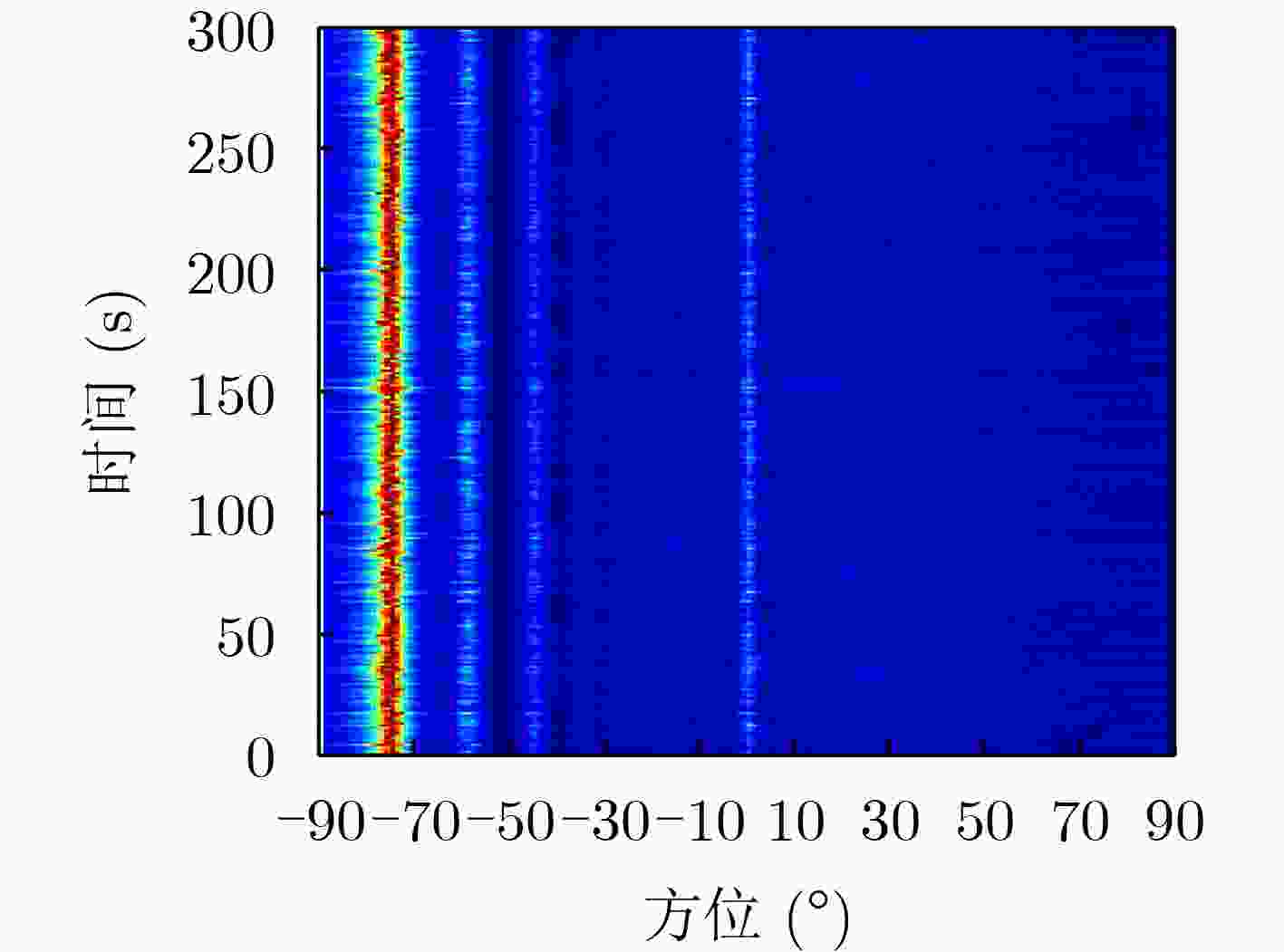
参数类型 参数设置 阵型 水平线列阵 阵元数量M 64 阵元间距 $ d $ 4 m 采样频率${f_{\rm{s}}}$ 5 kHz 正横方位$ \theta $ 0° 未知信源方位$ {\theta _0} $ $ - 70^\circ , - 50^\circ , - 30^\circ , - 10^\circ ,10^\circ ,30^\circ ,50^\circ ,70^\circ $ 工作频段${f_{\rm{B}}}$ 100~180 Hz -
[1] WANG Zengkun, YANG Zhibo, WU Shuming, et al. An improved multiple signal classification for nonuniform sampling in blade tip timing[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(10): 7941–7952. doi: 10.1109/TIM.2020.2980912 [2] KIJANKA P, QIANG Bo, SONG Pengfei, et al. Robust phase velocity dispersion estimation of viscoelastic materials used for medical applications based on the multiple signal classification method[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2018, 65(3): 423–439. doi: 10.1109/TUFFC.2018.2792324 [3] LI Jianfeng, ZHAO Gaofeng, LI Baobao, et al. A reduced dimension multiple signal classification–based direct location algorithm with dense arrays[J]. International Journal of Distributed Sensor Networks, To be published. [4] FENG Maoyuan, CUI Zhongma, YANG Yunxiu, et al. A reduced-dimension MUSIC algorithm for monostatic FDA-MIMO radar[J]. IEEE Communications Letters, 2021, 25(4): 1279–1282. doi: 10.1109/LCOMM.2020.3045440 [5] SHENG Xueli, LU Dian, LI Yingsong, et al. Performance improvement of bistatic baseline detection[J]. IETE Journal of Research, To be published. [6] JIANG Xingbang, NI Gang, CAO Anjie, et al. Single-channel spatial spectrum estimation direction finding by the time-modulated linear array[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(12): 2491–2495. doi: 10.1109/LAWP.2021.3115826 [7] YANG Bin, LI Wenxing, LI Yuanyuan, et al. Robust adaptive null broadening beamforming based on subspace projection[J]. International Journal of Electronics, 2023, 110(1): 184–198. doi: 10.1080/00207217.2021.2024608 [8] QI Bingbing and LIU Dunge. An enhanced spatial smoothing algorithm for coherent signals DOA estimation[J]. Engineering Computations, 2022, 39(2): 574–586. doi: 10.1108/EC-02-2021-0087 [9] ZHENG Guimei, CHEN Chen, and SONG Yuwei. Real valued MUSIC method for height measurement of meter wave polarimetric MIMO radar based on matrix reconstruction[J]. Remote Sensing, 2022, 14(16): 4121. doi: 10.3390/rs14164121 [10] WENG Liuqing, SONG Xiyu, LIU Zhenghong, et al. DOA estimation of indoor sound sources based on spherical harmonic domain beam-space MUSIC[J]. Symmetry, 2023, 15(1): 187. doi: 10.3390/sym15010187 [11] LI Jie, CHEN Fangjiong, WANG Yide, et al. Spatial spectrum estimation of incoherently distributed sources based on low-rank matrix recovery[J]. IEEE Transactions on Vehicular Technology, 2020, 69(6): 6333–6347. doi: 10.1109/TVT.2020.2986783 [12] 高杨, 李东生. 基于改良MUSIC和ALD-LCMV的自适应波束形成算法[J]. 探测与控制学报, 2015, 37(3): 24–29,39.GAO Yang and LI Dongsheng. Adaptive beamforming algorithm based on modified MUSIC and ADL-LCMV[J]. Journal of Detection &Control, 2015, 37(3): 24–29,39. [13] 王思秀, 郭文强, 汪晓洁, 等. 基于时空联合估计噪声子空间的MUSIC波束形成方法[J]. 计算机科学, 2021, 48(4): 282–287. doi: 10.11896/jsjkx.200300029WANG Sixiu, GUO Wenqiang, WANG Xiaojie, et al. MUSIC beam-forming method based on temporal and spatial union estimation of noise subspaces[J]. Computer Science, 2021, 48(4): 282–287. doi: 10.11896/jsjkx.200300029 [14] 司伟建, 林晴晴. 利用延时预处理的DOA估计方法[J]. 哈尔滨工程大学学报, 2012, 33(7): 894–898. doi: 10.3969/j.issn.1006-7043.201108047SI Weijian and LIN Qingqing. A method of DOA estimation based on delay preprocessing[J]. Journal of Harbin Engineering University, 2012, 33(7): 894–898. doi: 10.3969/j.issn.1006-7043.201108047 [15] 余华兵, 郑恩明, 陈新华. 基于相参累积预处理的空间谱估计方法[J]. 上海交通大学学报, 2020, 54(11): 1209–1217. doi: 10.16183/j.cnki.jsjtu.2019.332YU Huabing, ZHENG Enming, and CHEN Xinhua. A spatial spectrum estimation method based on coherent cumulative preprocessing[J]. Journal of Shanghai Jiao Tong University, 2020, 54(11): 1209–1217. doi: 10.16183/j.cnki.jsjtu.2019.332 [16] 邱岚. 基于两次傅里叶变换的时域MUSIC波达方向估计[J]. 电讯技术, 2018, 58(10): 1206–1211.QIU Lan. Time-domain MUSIC for DOA estimation based on twice Fourier transform[J]. Telecommunication Engineering, 2018, 58(10): 1206–1211. [17] 李冰, 汪永明, 黄海宁. 基于时域解析估计的多重信号分类波束形成方法[J]. 上海交通大学学报, 2019, 53(8): 928–935. doi: 10.16183/j.cnki.jsjtu.2019.08.006LI Bing, WANG Yongming, and HUANG Haining. Multiple signal classification beam-forming method based on time domain analysis[J]. Journal of Shanghai Jiao Tong University, 2019, 53(8): 928–935. doi: 10.16183/j.cnki.jsjtu.2019.08.006 [18] 武时龙. 基于分子阵预处理的最小方差无畸变响应波束形成方法[J]. 探测与控制学报, 2018, 40(6): 84–88.WU Shilong. Minimum variance undistorted response beam-forming algorithm based on sub-array preprocessing[J]. Journal of Detection &Control, 2018, 40(6): 84–88. [19] 余华兵, 郑恩明, 陈新华. 基于全相位预处理的时域多重信号分类波达方向估计方法[J]. 振动与冲击, 2020, 39(10): 242–248. doi: 10.13465/j.cnki.jvs.2020.10.033YU Huabing, ZHENG Enming, and CHEN Xinhua. The time-domain multiple signal classification DOA estimation method based on app-phase preprocessing[J]. Journal of Vibration and Shock, 2020, 39(10): 242–248. doi: 10.13465/j.cnki.jvs.2020.10.033 [20] 郑恩明, 陈新华, 宋春楠. 基于全相位预处理的低旁瓣波束形成方法[J]. 兵工学报, 2018, 39(10): 1971–1978. doi: 10.3969/j.issn.1000-1093.2018.10.013ZHENG Enming, CHEN Xinhua, and SONG Chunnan. Low side-lobe beam-forming method based on all-phase preprocessing[J]. Acta Armamentarii, 2018, 39(10): 1971–1978. doi: 10.3969/j.issn.1000-1093.2018.10.013 [21] 陈新华, 郑恩明. 基于分组时延预处理的时域波束形成方法[J]. 应用声学, 2019, 38(4): 545–552. doi: 10.11684/j.issn.1000-310X.2019.04.011CHEN Xinhua and ZHENG Enming. Time domain beam-forming algorithm based on sub-group & time delay preprocessing[J]. Journal of Applied Acoustics, 2019, 38(4): 545–552. doi: 10.11684/j.issn.1000-310X.2019.04.011 -





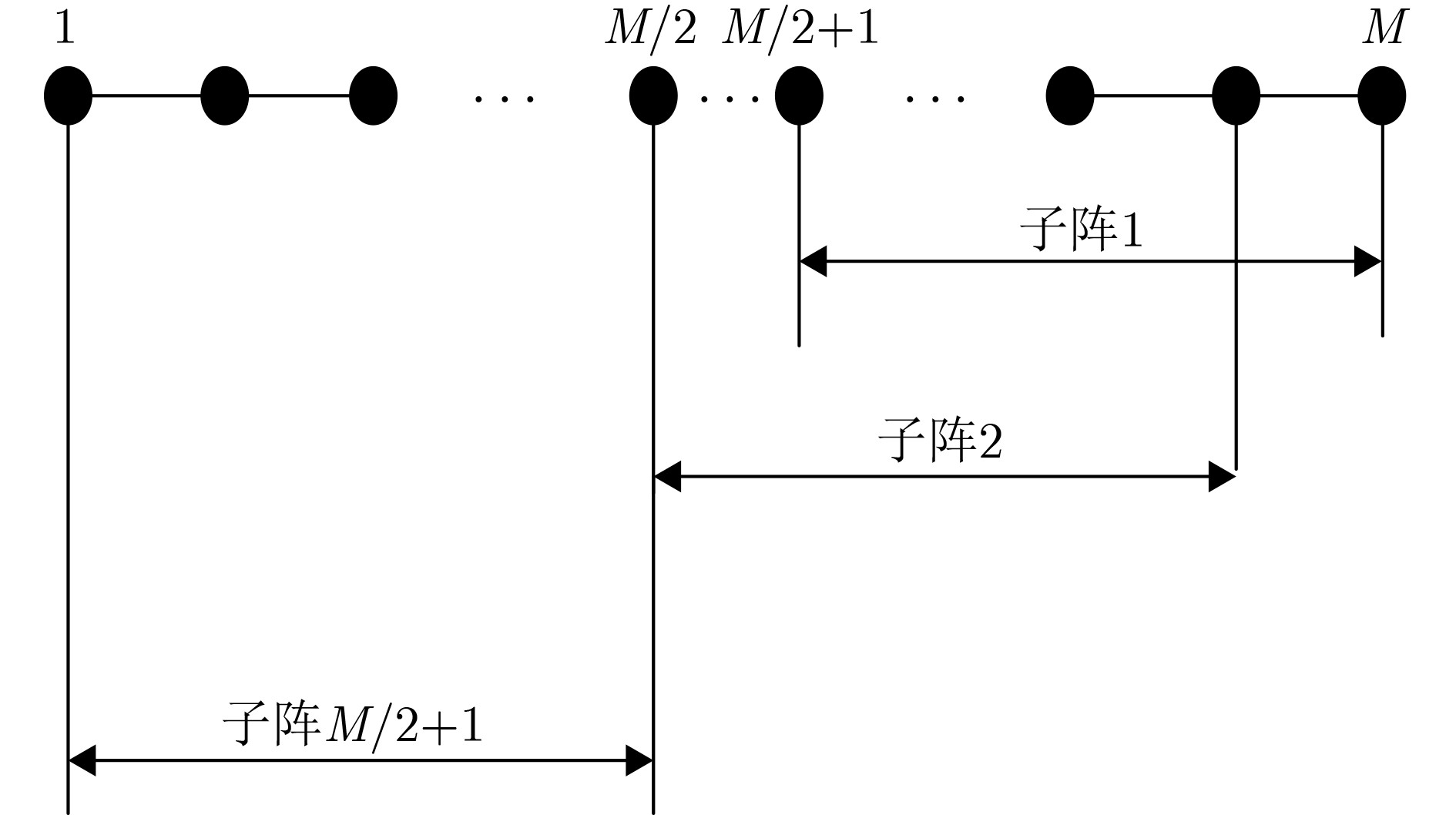
 下载:
下载:
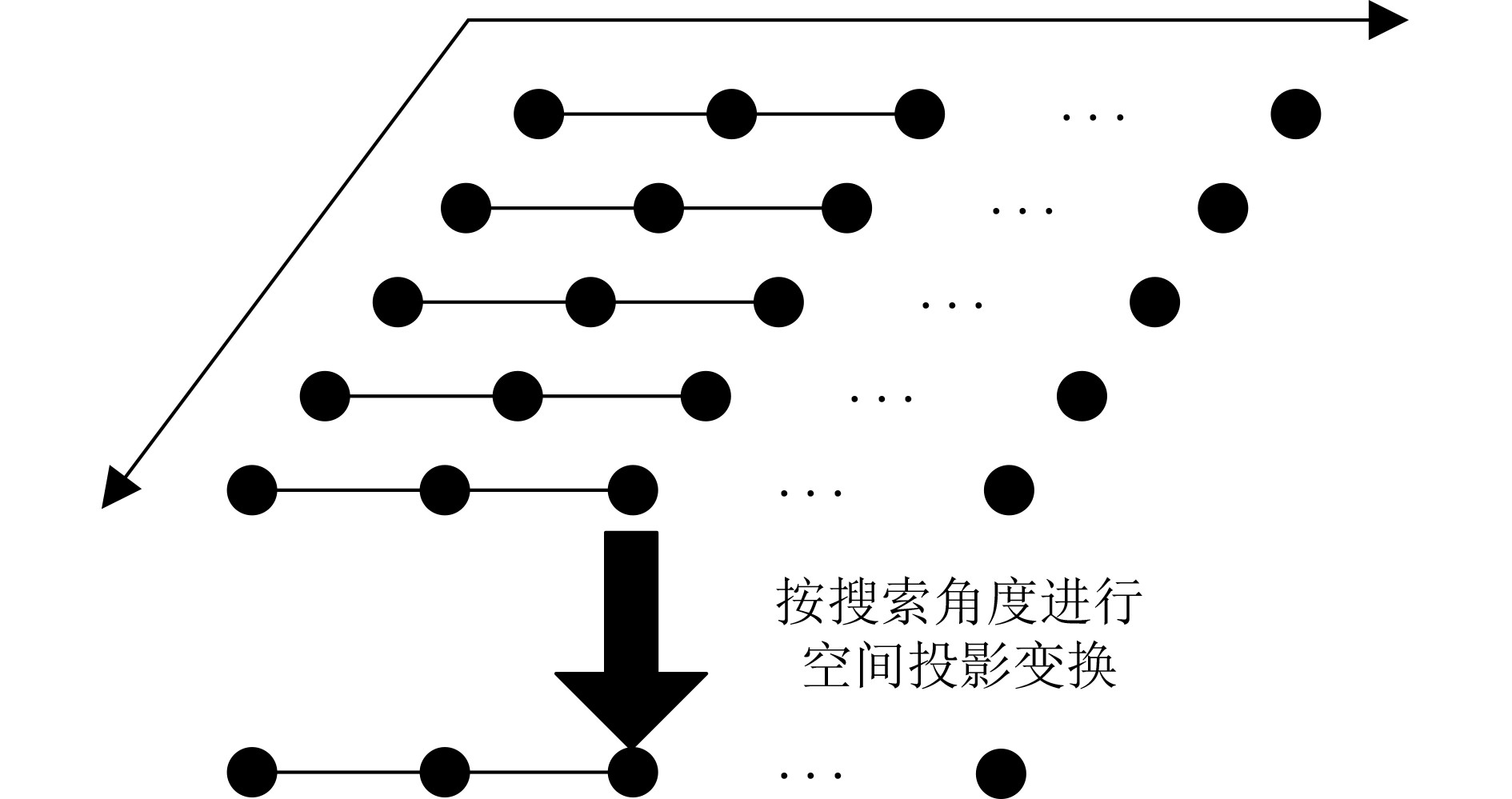
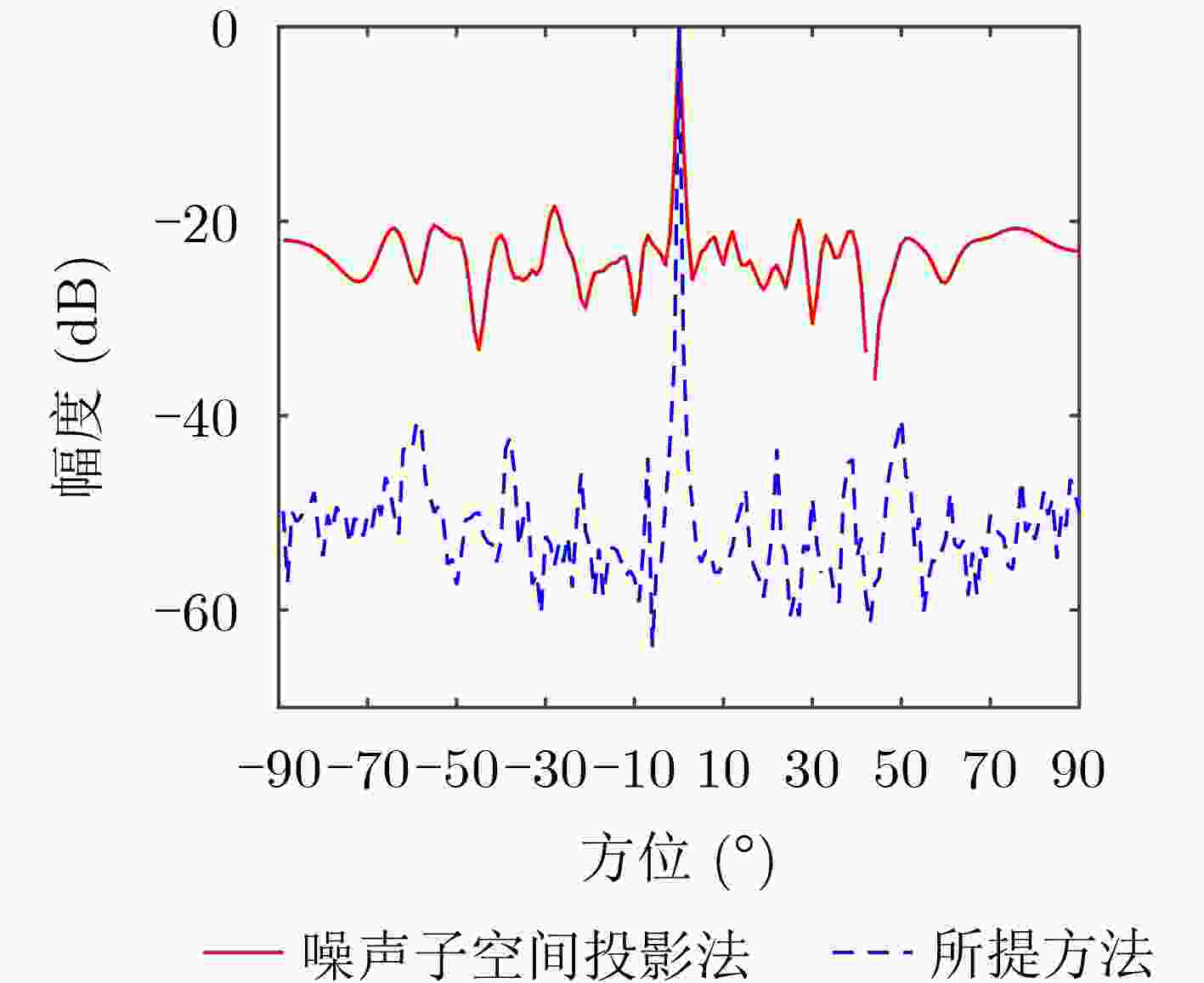

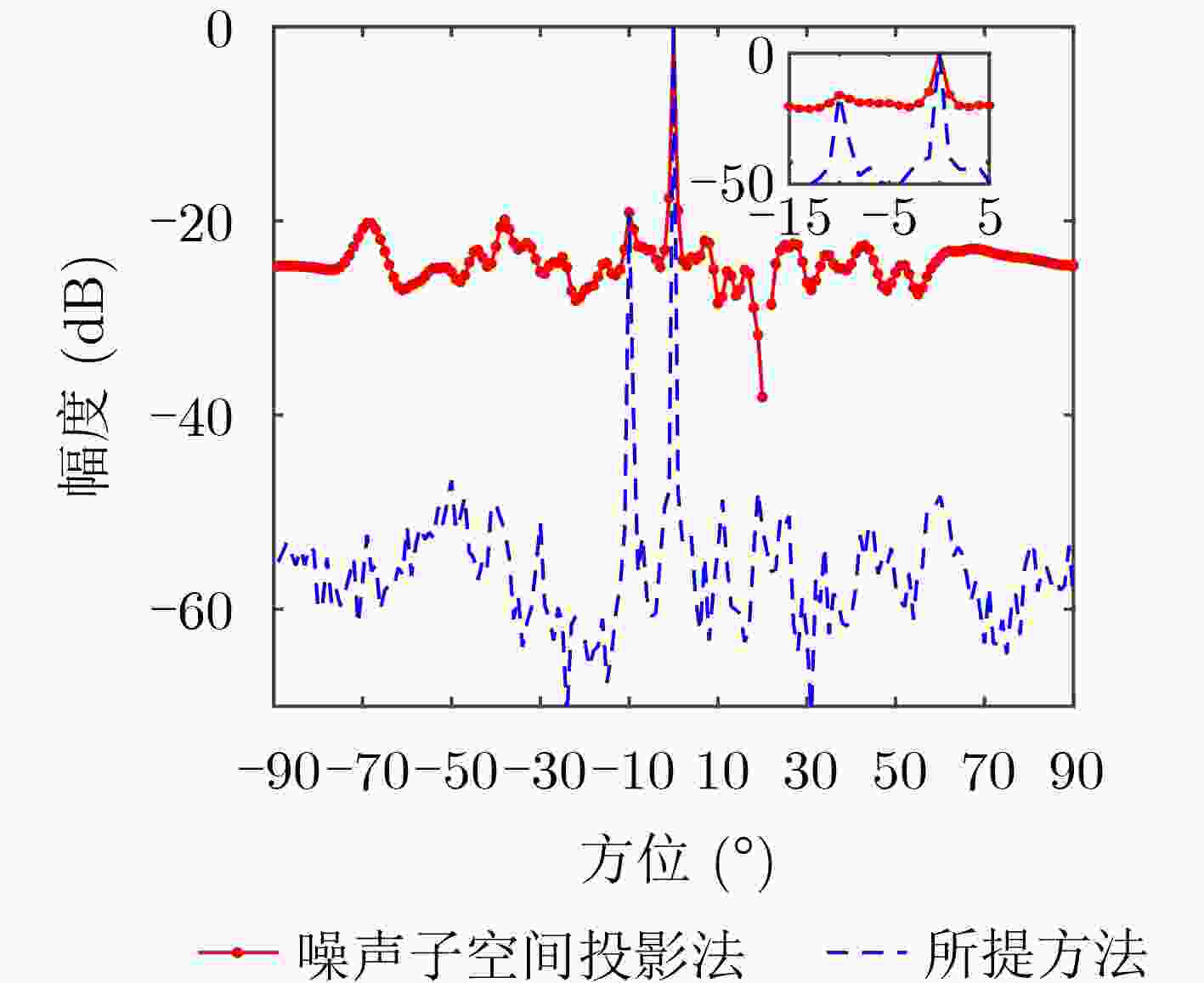


 下载:
下载:
