全同态加密软硬件加速研究进展

边松; 毛苒; 朱永清; 傅云濠; 张舟; 丁林; 张吉良; 张博; 陈弈; 董进; 关振宇

doi:10.11999/JEIT230448

全同态加密软硬件加速研究进展

doi: 10.11999/JEIT230448

边松¹,
毛苒¹,
朱永清¹,
傅云濠¹,
张舟¹,
丁林²,
张吉良²,
张博³,
陈弈³,
董进^3, ,,
关振宇^1, ,

1.
北京航空航天大学网络空间安全学院北京 100191
2.
湖南大学半导体学院(集成电路学院) 长沙 410000
3.
北京微芯区块链与边缘计算研究院北京 100080

基金项目: 国家重点研发计划(2023YFB3106200)，国家自然科学基金(62002006, 62172025, U21B2021, 61932011, 61932014, 61972018, 61972019, 62202028, U2241213)，国防基础科研项目(JCKY2021211B017)

详细信息

作者简介:
边松：男，副教授，研究方向为隐私计算、AI安全、应用密码学、硬件架构

毛苒：女，博士生，研究方向为隐私计算、全同态加密、硬件安全

朱永清：男，博士生，研究方向为全同态加密、硬件安全、隐私计算

傅云濠：男，硕士生，研究方向为全同态加密、硬件安全

张舟：男，硕士生，研究方向为全同态加密、隐私计算

丁林：男，博士生，研究方向为硬件安全、隐私计算及其专用芯片设计

张吉良：男，教授，研究方向为集成电路设计、集成电路硬件安全、后摩尔时代新型计算架构

张博：男，副研究员，研究方向为RISC-V开放架构芯片、区块链与隐私计算领域专用芯片、微型传感器芯片与系统方案设计

陈弈：男，副研究员，研究方向为集成电路设计、隐私计算软硬协同设计

董进：男，研究员，研究方向为区块链、隐私计算、人工智能、物联网、新型传感器

关振宇：男，教授，研究方向为硬件安全、区块链、视频压缩

通讯作者:
董进　dongjin@baec.org.cn

关振宇　guanzhenyu@buaa.edu.cn

中图分类号: TN918.4; TP309.2
计量
- 文章访问数: 2138
- HTML全文浏览量: 1015
- PDF下载量: 464
- 被引次数: 6
出版历程
- 收稿日期: 2023-05-18
- 修回日期: 2023-12-13
- 网络出版日期: 2023-12-22
- 刊出日期: 2024-05-30

A Survey on Software-hardware Acceleration for Fully Homomorphic Encryption

1.
School of Cyber Science and Technology, Beihang University, Beijing 100191, China
2.
College of Semiconductors (College of Integrated Circuits), Hunan University, Changsha 410000, China
3.
The Beijing Academy of Blockchain and Edge Computing, Beijing 100080, China

Funds: The National Key R&D Program of China (2023YFB3106200), The National Natural Science Foundation of China (62002006, 62172025, U21B2021, 61932011, 61932014, 61972018, 61972019, 62202028, U2241213), The Defense Industrial Technology Development Program (JCKY2021211B017)

摘要

摘要: 全同态加密(FHE)是一种重计算、轻交互的多方安全计算协议。在基于全同态加密的计算协议中，尽管计算参与方之间无需多轮交互与大量通信，加密状态下的密态数据处理时间通常是明文计算的 ${10}^{3}\mathrm{～}{10}^{6}$ 倍，极大地阻碍了这类计算协议的实际落地；而密态数据上的主要处理负担是大规模的并行密码运算和运算所必须的密文及密钥数据搬运需求。该文聚焦软、硬件两个层面上的全同态加密加速这一研究热点，通过系统性地归类及整理当前领域中的文献，讨论全同态加密计算加速的研究现状与展望。
- 全同态加密 /
- 同态算法 /
- 密码硬件加速
Abstract: Fully Homomorphic Encryption (FHE) is a multi-party secure computation protocol characterized by its high computational complexity and low interaction requirements. Although there is no need for multiple rounds of interactions and extensive communications between computing participants in protocols based on FHE, the processing time of encrypted data is typically ${10}^{3}$ to ${10}^{6}$ times of that of plaintext computing, and thus significantly hinders the practical deployment of such protocols. In particular, the large-scale darallel cryptographic operations and the cost of data movement for the ciphertext and key data needed in the operations become the dominating performance bottlenecks. The topic of accelerating FHE in both the software and the hardware layers is discussed in this paper. By systematically categorizing and organizing existing literatures, a survey on the current status and outlook of the research on FHE is presented.
- Fully Homomorphic Encryption(FHE) /
- Homomorphic algorithm /
- Cryptographic hardware acceleration

HTML全文

1. 引言

近年来，现场可编程门阵列(Field Programmable Gate Array, FPGA)广泛应用于各个领域，如深度学习^[1]、云计算^[2]和芯片设计的验证问题^[3]。复杂的专用集成电路(Application Specific Integrated Circuit, ASIC)芯片设计需要通过多种验证方法保证设计的正确性。验证的主要方法有软件仿真、形式化验证和硬件仿真。随着芯片设计越来越复杂，软件仿真需要花费大量的运行时间仿真每个逻辑电路，形式化验证难以适用于大型ASIC设计的验证问题，同时传统的硬件仿真方法需要花费大量的成本来实现验证。而基于FPGA原型验证的硬件仿真方法可以解决大型ASIC设计的验证问题，并且能够在成本和运行时间之间做到平衡。因此，许多先进的微处理器制造商在其验证过程中使用了基于FPGA原型验证的硬件仿真方法。

ASIC设计随着规模的不断扩大，越来越难在单个FPGA上实现逻辑验证^[4,5]。因此，大型的ASIC设计将根据设计需求被划分到多个FPGA内。与单FPGA系统相比，多FPGA系统逻辑复杂性更高，设计能力更强。高速收发器被运用于FPGA系统中，可以提高FPGA间的数据交换速度。随着FPGA内部构造越发复杂，FPGA间信号数量会远远超过I/O引脚数量。而时分复用(Time-Division Multiplexing, TDM)技术被广泛运用于解决I/O引脚数量不足的问题。然而，TDM技术会造成FPGA间的信号延迟，导致系统时延的增加。因此，减少TDM技术所导致的系统时延是十分重要的问题。

时分复用比率是用来衡量系统时钟周期使用情况的数值。在多FPGA原型系统的设计流程中，TDM比率通常是在FPGA布线后确定的。文献[6]提出了同时进行信号分割和分组的方法，可以优化分区和TDM比率。为了解决FPGA间的布线问题，文献[7]和文献[8]使用Pathfinder迭代地优化FPGA间的布线问题。然而，这两类工作都未考虑线网组的概念。文献[9]通过减少线长优化FPGA间的布线结果。然而，多FPGA系统的优化目标不仅仅是线长，TDM的比率分配也非常重要，因为系统性能很大程度上受到FPGA间线网的延迟影响。为了优化TDM比率，文献[10]提出了一种基于整数线性规划(Integer Linear Programming, ILP)的优化算法，但ILP只适合解决较小尺寸的问题。此外，以往工作中的TDM比率通常是任意整数，并不符合实际情况。

根据实际应用中的设计，本文提出一种用于时分复用技术的多阶段协同优化FPGA布线(Multi-Stage Co-optimization FPGA Routing, MSCOFRouting)方法，旨在满足TDM比率约束的前提下，布线拓扑生成阶段、TDM比率分配阶段和TDM比率优化阶段3个阶段协同优化FPGA间的可布线性和TDM比率。本文的主要贡献如下：

(1) 提出一种自适应布线算法，以避免布线拥塞，解决FPGA间布线优化问题，有力减少系统时延。

(2) 提出一种基于拉格朗日松弛(Lagrangian Relaxation, LR)的TDM比率分配算法，使小规模线网组获得较大TDM比率，大规模线网组获得较小TDM比率，有效解决TDM比率分配问题。

(3) 提出了一种TDM比率优化算法，缩减线网组和FPGA连接对的TDM比率。

(4) 将多线程并行化方法运用到上述3个算法，进一步提高MSCOFRouter的运行效率。

(5) 实验结果表明，本文算法不仅能满足TDM约束条件，而且可以获得比同类工作更好的解决方案。

后文组织如下：第2节介绍了时分复用技术和问题模型；第3节阐述了MSCOFRouting的整体框架。第4节给出本文相关策略的有效性验证及实验结果的比较分析。第5节总结全文。

2. 问题模型

2.1 时分复用技术

使用时分复用技术可以有效地解决I/O引脚数量不足的问题，使得多个信号可以在不同时间段共用一个I/O引脚。然而，使用时分复用技术会造成系统时延的增加。TDM比率是用来衡量系统时钟周期使用情况的数值，可以作为衡量系统时延的指标。系统时延与TDM比率呈单调递增关系。因此，通过降低TDM比率可以有效减少系统时延。FPGA连接对p上边e的时分复用比率如式(1)所示。

${\text{TR}}(e) = \frac{{{\text{DN}}(p)}}{{{\text{Cap}}(p)}}$

(1)

其中，DN(p), Cap(p)和TR(e)分别代表通过FPGA连接对p的信号数、FPGA连接对p的容量和边e的TDM比率。由于一个FPGA连接对间只有一根物理导线，所以FPGA连接对的容量固定为1。

图1是时分复用技术的示意图。图中的长方形、正方形和圆形分别表示转换器、实例和分区。红色箭头、蓝色箭头和绿色箭头分别表示3种不同的信号，两个FPGA中间的黑色箭头表示两个FPGA之间唯一的物理导线。在未使用时分复用技术的情况下，一个系统时钟周期内，一条物理导线只能传输一种信号。这会导致FPGA系统运行效率的下降。为了提升FPGA系统的运行效率，时分复用技术被运用在FPGA系统中，使得在一个系统时钟周期内可以传输3种不同的信号。

图 1 时分复用技术的示意图

下载: 全尺寸图片幻灯片

2.2 FPGA间的布线问题

2019年ICCAD比赛^[11,12]提出的FPGA间布线问题将FPGA系统中的FPGA抽象为节点，忽略了一些FPGA的特殊性，着重解决FPGA间的布线问题。本文常用的符号如表1所示。

表 1 常用符号

符号	含义
NG	所有线网组
N	所有线网
P	所有FPGA连接对
E	所有线网的边
Ne	经过边e的所有线网
ng_i	NG中第i个线网组
n_j	N中第j个线网
p_k	P中第k个FPGA连接对
ngl_j	包含n_j的线网组，ngl_j ⊆NG
ng_j,m	ngl_j中的第m个线网组
e_j,k	n_j中使用p_k的边
el_k	p_k的边
el_j	n_j的边
nl_i	ng_i的线网
α	线网组的数量
mng_j	ngl_j中带有最大TDM比率的线网组

下载: 导出CSV

| 显示表格

本节通过图2和表2的例子介绍FPGA间的布线问题。给定一组线网N和一组线网组NG。线网组是根据设计目的给定的。例如，具有相似属性或相同功耗的线网将在同一个线网组中。同时，给定一个无向图G，其中包括了多个由F表示的FPGA和多个由P表示的FPGA连接对。问题目标是根据无向图G对所有线网进行布线，并且为每条边分配合理的TDM比率，以最小化线网组的最大TDM比率。

图 2 TDM比率分配示意图

下载: 全尺寸图片幻灯片

表 2 线网组信息

线网组	线网	FPGA	示例
NG₁	N₁	F₃, F₄
NG₁	N₂	F₁, F₄
NG₂	N₃	F₁, F₂
NG₂	N₄	F₁, F₂
NG₃	N₁	F₃, F₄
NG₄	N₅	F₁, F₂
NG₅	N₆	F₂, F₃

下载: 导出CSV

| 显示表格

表2给出了线网N和线网组NG的信息，其中，不同的线网用不同颜色表示。图2(a)是一个结构图。f_i代表第i个FPGA，p_k代表第k个FPGA连接对。图2(b)是表1基于图2(a)所生成的布线结果。e_j,k代表线网n_j经过连接对p_k所布的边。连接对p_k间边的数量就是通过连接对p_k的信号数量。为了分析系统时延，每条边e_j,k应该被分配一个TDM比率。一个FPGA连接对应该满足TDM比率约束，如式(2)所示。

$\quad \sum\limits_{{{\text{e}}_{j,k}} \in {\text{e}}{{\text{l}}_k}} {\frac{1}{{{\text{et}}{{\text{r}}_{j,k}}}} \le 1}$

(2)

$\quad {\text{et}}{{\text{r}}_{j,k}} \in \left\{ {x\left| {x = 1 \times y,y \in {N^*},2 \le x} \right.} \right\}$

(3)

其中，etr_j,k表示e_j,k的TDM比率。如图1所示，由于所有的信号必须在半个周期内完成1次传输，故etr_j,k的值必须是偶数。每条边的TDM比率分配结果如图2(c)所示，对于p₁, e_2,1, e_3,1, e_4,1和e_5,1的TDM比率分别是4, 6, 6和10。由于1/4+1/6+1/6+1/10 <1，所以p₁满足TDM比率约束。

线网n_j的TDM比率和线网组ng_j的TDM比率定义为

${\text{nt}}{{\text{r}}_j} = \sum\limits_{{e_{j,k}} \in {\text{e}}{{\text{l}}_j}} {{\text{et}}{{\text{r}}_{j,k}}}$

(4)

${\text{gt}}{{\text{r}}_j} = \sum\limits_{{n_j} \in {\text{n}}{{\text{l}}_i}} {{\text{nt}}{{\text{r}}_j}}$

(5)

其中，ntr_j和gtr_j分别表示n_j的TDM比率和ng_i的TDM比率。如图2(c)所示，线网n₂上的边有e_2,1=4和e_2,3=2，所以ntr₂=etr_2,1+etr_2,3=2+4=6。线网组ng₂的包括n₃和n₄，所以gtr₂是12。

本文的优化目标是最小化TDM比率最大线网组的TDM比率，从而优化系统时延，具体如式(6)所示。

${\text{min}}:{\text{gmt}} = \left\{ {x|x = \max \left( {{\text{gt}}{{\text{r}}_1},\cdots,{\text{gt}}{{\text{r}}_a}} \right)} \right\}$

(6)

其中，gmt代表了TDM比率最大的线网组的TDM比率。如图2(c)所示，gmt是12。

3. 总体框架

用于时分复用技术的多阶段协同优化FPGA布线方法的总体框架如图3所示，分别为布线拓扑生成阶段、TDM比率分配阶段和TDM比率优化阶段3个阶段。具体地，第1阶段根据问题定义的线网和线网组进行布线，得到未分配TDM比率的布线结果。第2阶段使用拉格朗日松弛的方法为FPGA连接对的每条边分配初始的TDM比率。第3阶段通过松弛TDM比率较小的线网组，减小TDM比率倒数之和相对较小的FPGA连接对的最大TDM比率来优化TDM比率比较大的线网组。MSCOFRouting通过上述3个阶段协同优化FPGA的可布线性和TDM比率分配结果。

图 3 MSCOFRouting总体流程图

下载: 全尺寸图片幻灯片

3.1 布线拓扑生成

布线拓扑生成阶段的目标是根据给定的线网和线网组定义将每个线网的FPGA连接在一起。布线生成的Steiner树的质量会影响后续的TDM比率分配。由于Dijkstra算法可以有效构建Steiner树^[13,14]，因此本文使用基于Dijkstra算法的FPGA间布线算法连接所有线网，解决FPGA间的布线优化问题，使可布线性得到优化。算法中各变量的定义如下，f_s代表从F_n中选择的第1个FPGA、F_n表示线网n_j必须连接的目标FPGA、d表示两个FPGA间的布线代价、F_all表示所有FPGA、f_u表示与f_s布线代价最小的FPGA，f_v表示f_u的每个邻居FPGA, sp_v表示该线网的Steiner树。

自适应布线算法如下所示。由于线网所在的线网组中的线网数量和线网需要连接的FPGA数量对于线网的布线方案有重要的影响。所以所有线网都按照这两个指标进行排序。然后，初始化布线图，每个FPGA连接对的初始布线代价为1。最后，对所有的线网进行迭代布线。

对所有的线网进行迭代布线的具体步骤如下。首先，从F_n中选择一个FPGA赋值给f_s。其次，初始化F_n中各FPGA与f_s的距离。然后，集合F_all等于集合F。最后，通过Dijkstra算法构造Steiner树。Dijkstra算法首先找到与F_all中与f_s代价最小的FPGA f_u，然后更新集合F_all，最后更新f_u的所有邻居节点的布线代价d_v。当找到所有目标FPGA后，Steiner树被构造出来，把sp_x记录下来。Steiner树所使用的FPGA连接对的布线代价更新公式为

${\text{Tp}}'_k = \left\{ \begin{gathered} {\text{T}}{{\text{p}}_k} + {t_e},{\text{N}}{{\text{p}}_k} = 2t \\ {\text{T}}{{\text{p}}_k} + {t_o},{\text{N}}{{\text{p}}_k} = 2t + 1 \\ \end{gathered} \right.$

(7)

其中，Tp_k代表FPGA连接对的布线代价，Np_k代表FPGA连接对上已布线的边数，t_e和t_o分别表示FPGA连接对上已布线的边数为偶数和奇数的更新代价。实验得出t_e, t_o分别取0.81和1.19时优化效果最好。

图4只考虑两个FPGA间的布线情况。两个FPGA间有1条或者2条边时，每条边分配的TDM比率都是2，最大TDM比率都是2；当两个FPGA间有3条边时，每条边分配的TDM比率分别是2, 4, 4。当两个FPGA间有4条边时，每条边分配的TDM比率分别是4, 4, 4, 4。最大TDM比率都是4。由此可以得出结论：设i为奇数，当两个FPGA间有i条边时，布下1条边之后，最大TDM比率不变，为i+1；当两个FPGA间有i+1条边时，布下1条边之后，最大TDM比率值增加2，为i+3。所以布线代价更新式(7)可以减少两个FPGA间奇数条边的情况，优化布线结果，减少最大的TDM比率。

图 4 FPGA之间不同布线情况示意图

下载: 全尺寸图片幻灯片

3.2 TDM比率分配

TDM比率分配阶段需要为每条边分配满足约束的TDM比率并且使TDM比率最大的线网组的TDM比率最小化。在这一阶段，本文提出了一种基于拉格朗日松弛算法的TDM比率分配方法。

由于优化目标是将线网组中最大的TDM比率最小化，所以问题模型可以写成

$\left.\begin{aligned} & \mathop {{\text{min}}}\limits_{\text{t}} {\text{ gmt }} \\ & {\text{s}}{\text{.t}}{\text{. }}\sum\limits_{n \in N} {\sum\limits_{e \in E} {{\text{t}}{{\text{r}}_{{\text{ne}}}} \le {\text{gmt}}} } \\ & \quad\;\; \sum\limits_{n \in {\text{Ne}}} {\frac{1}{{{\text{t}}{{\text{r}}_{{\text{ne}}}}}} \le 1} \end{aligned}\right\}$

(8)

其中，gmt是布线图中TDM比率最大的线网组的TDM比率，tr_en是线网n中边e的TDM比率。本文将此公式称为主问题(Primal Problem, PP)。为了解决这个NP难问题，算法松弛第1个约束并引入非负拉格朗日乘数λ。λ作为违反约束的惩罚值。式(8)引入λ后可以得到

$L\left( {t,\lambda ,{\text{gmt}}} \right){\text{ = gmt + }}\sum\limits_{{\text{ng}} \in {\text{NG}}} {\lambda \left( \sum\limits_{n \in N} {\sum\limits_{e \in E} {{\text{t}}{{\text{r}}_{{\text{ne}}}}} } - {\text{gmt}}\right)}$

(9)

对于给定的拉格朗日乘数，拉格朗日乘数子问题LRS(λ)如式(10)所示。

$\left.\begin{aligned} & \mathop {{\text{min}}}\limits_{\text{t}} {\text{ }}L\left( {t,\lambda ,{\text{gmt}}} \right){\text{ }} \\ & {\text{s}}{\text{.t}}{\text{. }}\sum\limits_{n \in {\text{Ne}}} {\frac{1}{{{\text{t}}{{\text{r}}_{{\text{ne}}}}}} \le 1} \end{aligned}\right\}$

(10)

通过应用Karush-Kuhn-Tucker (KKT)条件以获得最优解，LRS(λ)问题可以简化为

$\left.\begin{aligned} & \mathrm{LRS}\text{*}\left(\lambda \right)：\underset{\text{t}}{\text{min}}\text{ }{\displaystyle \sum _{e\in E}{\displaystyle \sum _{n\in \text{Ne}}{\displaystyle \sum _{g\in {\text{NG}}_{n}}\lambda \times {\text{tr}}_{\text{ne}}}}}\\ & \qquad\qquad\quad \text{s}\text{.t}\text{. }{\displaystyle \sum _{n\in \text{Ne}}\frac{\text{1}}{{\text{tr}}_{\text{ne}}}\le 1} \end{aligned}\right\}$

(11)

拉格朗日对偶问题(Lagrangian Dual Problem, LDP)可以定义为

$\left.\begin{aligned} & {\text{max LRS*}}\left( \lambda \right) \\ & {\text{s}}{\text{.t}}{\text{. }}\sum\limits_{n \in {\text{Ne}}} {\frac{{\text{1}}}{{{\text{t}}{{\text{r}}_{{\text{ne}}}}}} \le 1} \end{aligned}\right\}$

(12)

对给定λ集合，求解LDP就是求解下界的最大值。LDP的主要目的是找到合适的λ集合惩罚PP中违反的约束。拉格朗日乘子根据时序弧的时序临界性更新，以满足KKT条件^[15-17]。更新公式为

${\lambda _i} = {\lambda _i} \times {\left( {{\text{TD}}{{\text{M}}_{i,g}}} \right)^{{K_{i,g}}}}$

(13)

其中，TDM_i,g为第i次迭代线网组g与最大线网组的TDM比率之比，K_i,g为第i次迭代的加速因子。加速因子越大，收敛速度越快，但是收敛效果越差。λ越接近目标值，加速因子应该越小。K_i,g的更新公式为

${K_{i,g}} = \frac{1}{{1 - ({{{\text{gm}}{{\text{t}}_i} - {\text{str}}}})/{{{\text{str}}}}}}$

(14)

其中，str是由用户定义的gmt的优化目标。

TDM比率分配算法如下所示。首先，计算边e_j,k的所在FPGA连接对边的数量。接着，计算线网组ng_i的λ_i。然后，根据λ集合计算线网n_i的snλ_i值，计算分配给每条边的TDM比率，再更新λ集合。最后，根据式(13)更新λ_i并根据式(14)更新K_i,g。

3.3 TDM比率优化

在TDM比率分配阶段，通过拉格朗日松弛算法得到的初始TDM比率并非最优解，还存在优化空间。因此，TDM比率优化阶段可以通过增加TDM比率较小的线网组边的TDM比率以减少TDM比率较大的线网组边的TDM比率，并可以针对具体连接对进行优化系统时延，从而使TDM比率最大的线网组的TDM比率最小化。

TDM比率优化算法包括3个步骤。第1步是缩减操作。具体是增加TDM比率较小的线网组的TDM比率，减少TDM比率较大的线网组的TDM比率。第2步是合法化操作。经过缩减步骤后，TDM比率增加的FPGA连接对可能会违反TDM比率约束。因此，违反约束的FPGA连接对需要进行合法化操作。第3步是针对性优化操作。经过上述步骤后，所有FPGA连接对的TDM比率的倒数和与最大值1还有一定距离。通过减少连接对中TDM比率最大的etr_j,k的方式，使得每个FPGA连接对的TDM比率倒数和更接近1，从而使TDM比率最大的线网组的TDM比率更小。

缩减操作的具体步骤如下所示。首先，所有线网按其所在线网组的最大TDM比率从大到小排序。然后，线网n_j中每条边的TDM比率 ${\text{etr}}{'_{j,k}}$ 根据以下公式更新。

$\begin{split} & {\text{etr}}{'_{j,k}} \\ & = \left\{ \begin{gathered} {\text{et}}{{\text{r}}_{j,k}} + {f} \left( {\left( {\frac{{{\text{mn}}{{\text{g}}_j}}}{{{\text{str}}}} - 1} \right) \times {\text{et}}{{\text{r}}_{j,k}}} \right),{\text{mn}}{{\text{g}}_j} < {\text{str}} \\ {\text{et}}{{\text{r}}_{j,k}} - {g} \left( {\left( {1 - \frac{{{\text{mn}}{{\text{g}}_j}}}{{{\text{str}}}}} \right) \times {\text{et}}{{\text{r}}_{j,k}}} \right),{\text{mn}}{{\text{g}}_j} > {\text{str}} \\ \end{gathered} \right. \end{split}$

(15)

其中， ${\text{etr}}{'_{j,k}}$ 是e_j,k新的TDM的比率。f(x)表示大于等于x的最小偶数，g(x)表示小于等于x的最大偶数。

线网n_j的TDM比率减少后，更新ngl_j中各线网组的TDM比率，有利于后续的缩减。

第2步是对FPGA连接对进行合法化操作。经过缩减步骤，TDM比率增加的边e_j,k可以直接使用新的TDM比率 ${\text{etr}}{'_{j,k}}$ ；对于TDM比率减小的边e_j,k，如果p_k满足TDM比率约束，则用 ${\text{etr}}{'_{j,k}}$ 替换对应的p_k中的每条边的etr_j,k。然而，如果p_k不满足TDM比率约束，应由式(16)合法化。

${\text{etr}}{''}_{j,k} = \frac{{{\text{etr}}'_{j,k} \times {\text{rec}} \times ({\text{rec}} + {\text{ad}})}}{{1 - {\text{ad}}}}$

(16)

其中，rec是 ${\text{etr}}'_{j,k}$ 减少的倒数之和，ad是 ${\text{etr}}'_{j,k}$ 增加的倒数之和。

算法第3步是减小具体FPGA连接对的最大TDM比率。经过前两个阶段后，当FPGA连接对边的TDM比率倒数和res_k小于0.95时，这个FPGA连接对的最大TDM比率由式(17)进行更新。

${\text{elt}}'_{k,{\rm{max}}} = \frac{{{\text{el}}{{\text{t}}_{k,\max }}}}{{\left( {1 - {\text{re}}{{\text{s}}_k}} \right) \times {\text{el}}{{\text{t}}_{k,\max }} + 1}}$

(17)

其中，res_k是FPGA连接对p_k上TDM比率倒数和，elt_k,max是FPGA连接对p_k上最大的TDM比率。

如果在缩减步骤中，当mng_j > str，减少的部分都向下取偶数会使得当前FPGA连接对的TDM倒数和更小，更有利于第3步FPGA连接对中最大TDM比率的减小。比如，当有3个线网组的TDM比率为4, 14和24，优化的目标值为8。如果不论mng_j是否大于str，变化值都向上取偶数，经过缩减阶段得出的TDM比率是6, 10和16，TDM倒数和为0.329；如果按照式(15)优化TDM比率，得到的TDM比率是6, 12和16，TDM倒数和为0.25。后者TDM比率倒数和小于前者，更有利于第3步FPGA连接对最大TDM比率的减小。所以选择式(15)的缩减方式。

3.4 多线程并行化

为了提高布线器的效率，使用并行编程模型OpenMp在布线器的各个阶段集成多线程并行化方法。编译器通过识别编译制导语句自动创建线程进行并行化，从而有效提高算法的效率。在布线拓扑生成阶段，各线网的布线操作可以并行执行。在TDM比率分配阶段，每个线网的TDM比率分配都是完全独立的。因此，这个阶段可以对不同线网进行并行化操作。在系统时延优化阶段，每个线网的缩减操作都是并行的。合法化操作和针对性优化中不同FPGA连接对可以并行处理。但是，由于不同线网之间存在资源冲突，自适应布线算法的记录sp_x操作和TDM比率优化算法的更新ngl_j中各线网组的TDM比率操作应该加锁。通过对上述3个阶段使用多线程并行化方法可以有效减少算法运行时间。

4. 实验结果

所提出的优化框架采用C/C++语言实现，并在Intel Xeon Linux服务器上运行。本文在2019年的ICCAD竞赛^[12]发布测试用例上展开实验。该测试用例将FPGA系统中的FPGA抽象为节点，忽略了一些FPGA的特殊性，着重解决FPGA间的布线问题。所以本文算法可以解决不同FPGA的布线问题，具有普适性。表3为测试用例具体信息，其中#FPGA表示FPGA数量，#Net表示线网数量，#NG表示线网组数量，#Edge表示FPGA连接对数量。

表 3 测试用例信息

测试用例	#FPGA	#Net	#NG	#Edge
S1	43	68456	40552	214
S2	56	35155	56308	157
S3	114	302956	334652	350
S4	229	551956	464867	1087
S5	301	881480	879145	2153
S6	410	785539	910739	1852
H1	73	54310	50417	289
H2	157	610675	501594	803
H3	487	720520	886720	2720

下载: 导出CSV

| 显示表格

4.1 与ALIFRouter及MSFRoute的实验比较

本节参考ICCAD2019比赛^[12]的计算评估分数公式将MSCOFRouting与ALIFRouter^[11]及MSFRoute^[18]进行比较。为了强调运行时间的影响，计算评估分数时考虑了运行时间。评估分数sco计算公式为

${\text{sco}} = {\text{TR}} \times \left( {1 + \lg \frac{{{\text{RT}}}}{{{\text{MRT}}}} \times 0.01} \right)$

(18)

其中，TR为TDM最大的线网组的TDM比率，RT为运行时间，MRT为3个布线器运行时间的中位数。sum为所有测试用例的sco之和。布线器的sum越小表示它的优化效果越好。

如表4所示，MSCOFRouting获得了最好的sum，并且达到了最好的TDM比率和运行时间。与MSFRoute和ALIFRouter相比，MSCOFRouting的TDM比率分别降低了4.57%和1.05%，运行时间分别缩短了20.8%和0.44%。由于每个标准测试用例涉及多个线网组，总的布线边数量非常多，因此时钟周期数的基数很大，TDM比率数值很大。虽然TDM比率的优化率较小，但是TDM比率优化值较大，系统时延的优化效果较好，所以实验结果表明MSCOFRouting可以有效优化系统时延。

表 4 本文算法与ALIFRouter及MSFRoute的实验比较(TR为TDM Ratio)

测试用例	MSFRoute			ALIFRouter			本文算法
测试用例	TR(10³)	RT	sco	TR(10³)	RT	sco	TR(10³)	RT	sco
S1	39	34.32	39	38	24.88	38	37	30.58	37
S2	32097	20.51	32097	31736	19.58	31730	31671	20.86	31673
S3	129396	289.91	129375	127826	304.50	127832	127046	300.99	127046
S4	7301	642.51	7301	6466	641.62	6466	6312	619.88	6311
S5	5370	1673.51	5371	4766	1558.48	4766	4618	1570.51	4618
S6	15759857	4536.33	15757896	15751307	4668.18	15751307	15747236	4845.90	15749791
H1	409654	76.86	409661	409026	76.54	409026	408487	66.81	408246
H2	45947775	1322.96	45947798	45942757	1322.81	45942757	45934257	1217.81	45917758
H3	4871917	5283.91	4868324	4866484	6593.58	4867575	4861401	6261.79	4861401
sum	–	–	62289539	–	–	62273922	–	–	62245480
Normalized	1.0457	1.0208	–	1.0105	1.0044	–	1.0000	1.0000	–

下载: 导出CSV

| 显示表格

4.2 多线程并行化方法的有效性验证

MSCOFRouting在不同线程数下的运行时间如图5所示。不同的线段表示不同测试用例的运行时间。本节在具有典型性的中等规模测试用例S3, S4和H2上展开实验。通过使用8个线程、16个线程、24个线程和多线程并行化方法，MSCOFRouting分别可以得到3.11倍、3.82倍和4.08倍的加速。各线网间存在共用同一变量的情况。为了避免多个线程同时修改变量而导致数据错误，则需要对共享变量进行加锁操作。如果同时运行中的线程需要用到已使用的共享变量，则需要等待正在使用该资源的线程运行结束。所以随着线程数的增多，等待共享变量的时间逐渐增加，运行时间的优化率逐渐减少。

图 5 并行化方法有效性折线图

下载: 全尺寸图片幻灯片

4.3 自适应布线算法有效性验证

为了验证自适应布线算法的有效性，本节将采用不同更新代价的自适应布线算法与未采用自适应布线算法的最大TDM比率进行比较。表5为采用不同权重值的自适应布线算法的实验结果。数据都是从同一环境中由8个线程运行的程序中获得的。表5中△TR的优化率的计算公式为

表 5 自适应布线算法有效性验证

测试用例	采用(t_e=1, t_o=1)		采用(t_e=0.21, t_o=1.79)		采用(t_e=0.2, t_o=1.8)		采用(t_e=0.19, t_o=1.81)		采用(t_e=0.18, t_o=1.82)
测试用例	△TR(10³)	Ratio	△TR(10³)	Ratio	△TR(10³)	Ratio	△TR(10³)	Ratio	△TR(10⁴)	Ratio
S1	1	1.0000	1	1.0000	1	1.0000	2	2.0000	1	1.0000
S2	375	1.0000	417	1.1120	423	1.1280	428	1.1413	412	1.0987
S3	1841	1.0000	1864	1.0125	1948	1.0581	1986	1.0788	1941	1.0543
S4	832	1.0000	857	1.0300	931	1.1190	950	1.1418	927	1.1142
S5	604	1.0000	627	1.0381	697	1.1540	717	1.1871	687	1.1374
S6	11574	1.0000	13614	1.1763	12001	1.0369	12009	1.0376	12004	1.0372
H1	798	1.0000	801	1.0038	807	1.0113	812	1.0175	808	1.0125
H2	7742	1.0000	7785	1.0056	7795	1.0068	7821	1.0102	7801	1.0076
H3	6214	1.0000	6245	1.0050	9521	1.5322	10098	1.6250	9457	1.5219
平均	–	1.0000	–	1.0426	–	1.1163	–	1.2488	–	1.1093

下载: 导出CSV

| 显示表格

$\Delta {\text{T}}{{\text{R}}_{{t_e} = x}} = {\text{T}}{{\text{R}}_{{t_e} = x}} - {\text{T}}{{\text{R}}_{{\text{MSF}}}}$

(19)

不同的更新代价分别将△TR比率的优化率增加4.26%, 11.63%, 4.88%和10.93%。根据实验结果可知，当t_e=0.19, t_o=1.81时，自适应布线算法效果最好。由于较好的布线结果较少出现布线拥塞的情况，从而减少最大TDM比率。因此通过这些△TR的优化率可以得出自适应布线算法可以有效避免布线拥塞的情况出现，解决FPGA间的布线优化问题，优化布线结果，有效地减少系统时延。

4.4 LR分配算法和TDM比率优化算法有效性验证

本节将TDM比率分配算法和TDM比率优化算法运用到当前最先进的FPGA布线器ALIFRouter中进行比较。表6为LR分配算法和多层次的TDM比率优化算法的实验结果，并与ALIFRouter的实验数据进行对比。数据都是从同一环境中由8个线程运行的程序中获得的。表格中△TR的优化率是由MSFRoute在各测试用例上得到的线网组的最大TDM比率减去使用ALIFRouter、使用TDM比率分配算法和使用TDM比率优化算法后获得的最大TDM比率计算得到的。与ALIFRouter相比，两种算法可分别将ΔTR比率的优化率增加8.85%和10.39%。这些ΔTR的优化率表明LR分配算法和TDM比率优化算法可以有效地降低系统时延。

表 6 LR分配算法(即TDM比率分配算法)和TDM比率优化算法有效性验证

测试用例	ALIFRouter		只使用LR分配算法		只使用TDM比率优化算法
测试用例	△TR(10³)	Ratio	△TR(10³)	Ratio	△TR(10³)	Ratio
S1	1	1.0000	1	1.0000	1	1.0000
S2	384	1.0000	421	1.0964	419	1.1607
S3	1877	1.0000	1960	1.0442	2155	1.3726
S4	848	1.0000	889	1.0483	937	1.1222
S5	621	1.0000	635	1.0225	690	1.1424
S6	11994	1.0000	18550	1.5466	11989	1.4022
H1	799	1.0000	804	1.0063	804	0.0022
H2	7775	1.0000	7776	1.0001	7776	1.5496
H3	6220	1.0000	6419	1.0320	6429	1.1833
平均	–	1.0000	–	1.0885	–	1.1039

下载: 导出CSV

| 显示表格

5. 结束语

针对FPGA系统中运用TDM技术后导致系统时延增加的问题，本文提出了一种用于时分复用技术的多阶段协同优化FPGA布线方法，通过布线拓扑生成阶段、TDM比率分配阶段和TDM比率优化阶段3个阶段协同优化FPGA的可布线性和TDM比率分配结果。首先，为了生成高质量的布线拓扑，避免布线拥塞，解决FPGA间的布线优化问题，提出了自适应布线算法。其次，使用基于拉格朗日松弛的TDM比率分配算法，为布线图的边分配系统时延更小的初始TDM比率。然后，为了进一步减小最大线网组的TDM比率，通过一种多层次的TDM比率优化算法，同时缩减线网组和FPGA连接对的TDM比率。并且，为了提高MSCOFRouting的运行效率，在上述3个算法中使用多线程并行化方法，降低算法的运行时间。实验结果表明，与同类布线器相比，本文提出的MSCOFRouting能够获得最佳的系统时延优化质量。未来的工作中，将扩展本文算法应用到考虑带高速收发器的FPGA系统的TDM比率优化问题。

图 1 全同态加密研究进展概述

下载: 全尺寸图片幻灯片

图 2 BGV自举流程

下载: 全尺寸图片幻灯片

图 3 CKKS自举流程

下载: 全尺寸图片幻灯片

图 4 TFHE自举流程算法1 同态累加

下载: 全尺寸图片幻灯片

图 5 同态矩阵-向量乘法

下载: 全尺寸图片幻灯片

图 6 可编程自举中的盲旋转

下载: 全尺寸图片幻灯片

图 7 F1加速器硬件架构

下载: 全尺寸图片幻灯片

图 8 MATCHA架构

下载: 全尺寸图片幻灯片

表 1 符号定义

符号	描述	符号	描述
$\lambda$	安全参数	$\chi$	噪声分布
$p$	明文模数	$\mathbb{Z}_q^n$	$\mathbb{Z}_q^n$ 上的 $n$ 维向量
$q$	LWE密文模数	$R$	$\mathbb{Z}[X]/\left( {{X^N} + 1} \right)$ 上的分圆多项式环
$Q$	RLWE密文模数	${R_Q}$	${\mathbb{Z}_Q}[X]/\left( {{X^N} + 1} \right)$ 上的分圆多项式环
$Q'$	GSW密文模数	${\boldsymbol{a}}$	向量域上的元素
$n$	LWE密文维数	${a_i}$	$a$ 的第 $i$ 个元素
$N$	RLWE密文维数	$\tilde a$	多项式环上的元素
$N^{\prime}$	GSW密文维数	${\tilde {\boldsymbol{a}}_i}$	多项式环 $\tilde {\boldsymbol{a}}$ 的第 $i$ 元素
$l$	GSW中包含RLWE个数	${{\mathrm{LWE}}}_{\boldsymbol{s}}^{n,q}({\boldsymbol{m}})$	参数 $\left( {n,q} \right)$ 和密钥 ${\boldsymbol{s}}$ 加密消息 ${\boldsymbol{m}}$ 的LWE密文
$\Delta$	缩放因子	${\text{RLWE}}_{{\boldsymbol{\tilde s}}}^{N,Q}({\boldsymbol{\tilde m}})$	参数 $\left( {N,Q} \right)$ 和密钥 ${\boldsymbol{\tilde s}}$ 加密消息 ${\boldsymbol{\tilde m}}$ 的RLWE密文
$\varkappa$	自举中未被刷新的位数	${\text{RGSW}}_{{\boldsymbol{\tilde s}}}^{N',Q'}({\boldsymbol{m}})$	参数 $\left( {N',Q'} \right)$ 和密钥 ${\boldsymbol{\tilde s}}$ 加密消息 ${\boldsymbol{m}}$ 的RGSW密文
$\vartheta$	自举置零的位数	$d \leftarrow \mathcal{D}$	从分布 $\mathcal{D}$ 中随机选择一个元素 $d$

下载: 导出CSV

算法1　同态累加
ACC $\leftarrow b$
For $i = 1$ to $n$ do
${\text{ACC}} \leftarrow {\text{ACC}} - {\text{B}}{{\text{K}}_i} \cdot {a_i}{\rm{mod}} q$
End
ReturnACC

下载: 导出CSV

表 2 全同态加密体系对比

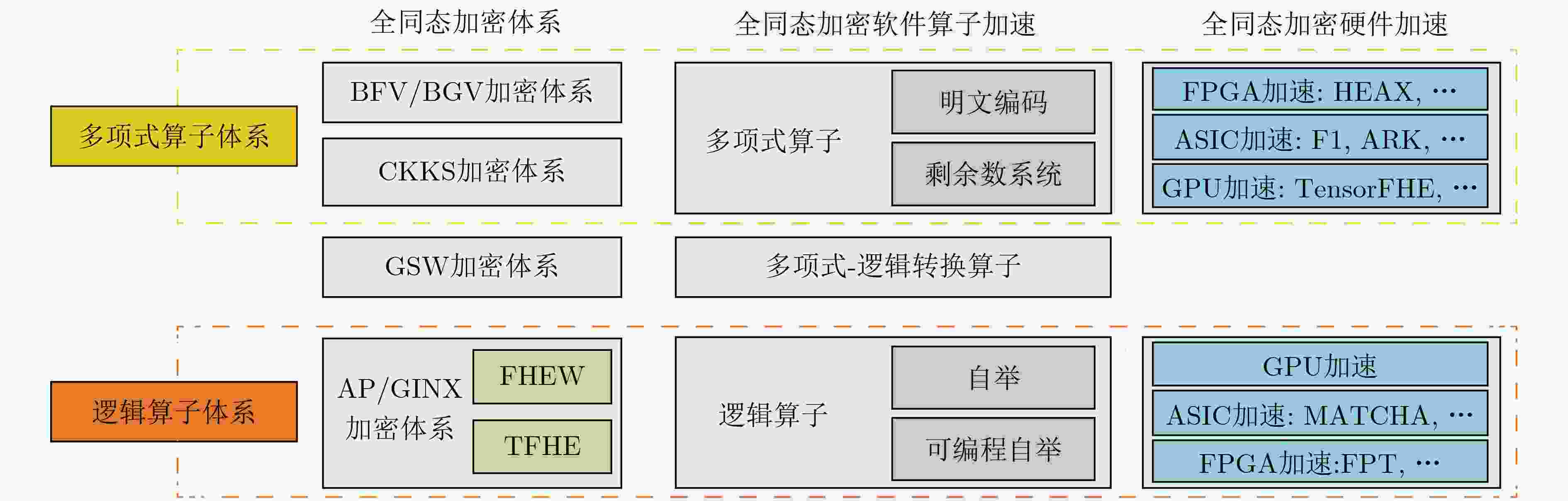
加密体系	线性计算	非线性计算	批处理	特点及应用
BFV/BGV加密体系	√	×	√	整数运算，标量乘法，高效层级同态设计
CKKS加密体系	√	△	√	实数运算，多项式近似，离散傅里叶变换
AP/GINX加密体系	√	√	×	比特运算，快速自举，布尔电路

下载: 导出CSV

表 3 近期全同态加密算法的硬件加速方案

年份	加速方案	实验平台	面向算法	实验效果
2020	HEAX^[60]	FPGA	CKKS	与单线程Intel Xeon(R) Silver 4108处理器相比较，HEAX可以实现164～268倍的性能提升
2021	Cheetah^[61]	40 nm ASIC	BFV	相较于当时最好的面向神经网络的同态加密接口解决方案Gazelle^[23]，综合电路可提供约79倍的加速效果
2021	F1^[62]	14 nm/12 nm ASIC	BGV, BFV, GSW, CKKS	性能相较于4核心8线程的3.5 GHz Xeon E3-1240v5 CPU软件实现方案速度平均提高了5400倍，其中最高的可达17000倍，并且比当时最快的硬件加速方案HEAX^[60]快了172到1866倍不等
2022	CraterLake^[63]	14 nm/12 nm ASIC	BGV, GSW, CKKS	性能比CPU(32核64线程3.5 GHz AMD Ryzen Threadripper PRO 3975WX)平均高出4600倍，比之前的最佳全同态加密加速器F1^[62]高出11.2倍
2022	ARK^[64]	7 nm ASIC	CKKS	相较于CPU(2.6 GHz Xeon Platinum 8358)单线程软件实现速度提升了最高18 214倍，相较于GPU实现方案100x^[65]在一些算子上提升了104～563倍，相较于CraterLake^[63]速度提升了1.23～2.58倍
2023	Poseidon^[66]	FPGA	CKKS	对于全同态加密基本运算，Poseidon相较于现有的单线程CPU(3.3 GHz Intel Xeon Gold 6 234)的加速比高达370倍；对于关键算子，Poseidon相较于CPU和FPGA解决方案HEAX^[60]的加速比分别高达1300倍和52倍；对于全同态加密基准测试，Poseidon相较于GPU解决方案100x^[65]和ASIC解决方案F1^[62]的加速比分别高达10.6倍和8.7倍
2023	FxHENN^[67]	FPGA	CKKS	与最先进的基于CPU的HE-CNN推理解决方案LoLa^[68]相比，FxHENN实现了高达13.49倍的推理延迟加速效果和1 187.12倍的能量效率
2023	TensorFHE^[69]	GPU	BFV, BGV	比GPGPU上最先进的全同态加密实现100x^[4]快 2.61 倍;在特定的工作负载下，TensorFHE可以比 F1+^[62]快 2.9 倍
2022	MATCHA^[70]	16 nm ASIC	TFHE	与实现的GPU同态运行库cuFHE^[71]相比，将TFHE门处理吞吐量提高了2.3倍；与FPGA方案TVE^[72]改造的ASIC加速器相比，在能效上将每瓦特吞吐量提高了6.3倍
2022	FPT^[73]	FPGA	TFHE	FPT的自举吞吐量比现有基于CPU(2.1 GHz Intel Xeon Silver 4208 CPU)的单核实现高近937倍，比FPGA方案^[74]高出7.1倍，并且比最近的ASIC方案MATCHA^[8]高出2.5倍。

下载: 导出CSV

参考文献(80)

[1]	GOLDREICH O, MICALI S, and WIGDERSON A. How to play any mental game[C]. The Nineteenth Annual ACM Symposium on Theory of Computing, New York, USA, 1987: 218–229. doi: 10.1145/28395.28420.
[2]	YAO A C C. How to generate and exchange secrets[C]. The 27th Annual Symposium on Foundations of Computer Science, Toronto, Canada, 1986: 162–167. doi: 10.1109/SFCS.1986.25.
[3]	GENTRY C. Fully homomorphic encryption using ideal lattices[C]. The Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, USA, 2009: 169–178. doi: 10.1145/1536414.1536440.
[4]	HUANG Zhicong, LU Wenjie, HONG Cheng, et al. Cheetah: Lean and fast secure two-party deep neural network inference[C]. The 31st USENIX Security Symposium, Boston, USA, 2022: 809–826.
[5]	LU Wenjie, HUANG Zhicong, HONG Cheng, et al. PEGASUS: Bridging polynomial and non-polynomial evaluations in homomorphic encryption[C]. 2021 IEEE Symposium on Security and Privacy, San Francisco, USA, 2021: 1057–1073. doi: 10.1109/SP40001.2021.00043.
[6]	韦韬, 潘无穷, 李婷婷, 等. 可信隐私计算: 破解数据密态时代“技术困局”[J]. 信息通信技术与政策, 2022, 48(5): 15–24. doi: 10.12267/j.issn.2096-5931.2022.05.003. WEI Tao, PAN Wuqiong, LI Tingting, et al. Trusted-environment-based privacy preserving computing: Breaks the bottleneck of ciphertext-exchange era[J]. Information and Communications Technology and Policy, 2022, 48(5): 15–24. doi: 10.12267/j.issn.2096-5931.2022.05.003.
[7]	FAN Junfeng and VERCAUTEREN F. Somewhat practical fully homomorphic encryption[R]. Cryptology ePrint Archive 2012/144, 2012.
[8]	BRAKERSKI Z, GENTRY C, and VAIKUNTANATHAN V. (Leveled) fully homomorphic encryption without bootstrapping[J]. ACM Transactions on Computation Theory, 2014, 6(3): 13. doi: 10.1145/2633600.
[9]	CHEON J H, KIM A, KIM M, et al. Homomorphic encryption for arithmetic of approximate numbers[C]. The 23rd International Conference on the Theory and Application of Cryptology and Information Security, Hong Kong, China, 2017: 409–437. doi: 10.1007/978-3-319-70694-8_15.
[10]	GENTRY C, SAHAI A, and WATERS B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based[C]. The 33rd Annual Cryptology Conference, Santa Barbara, USA, 2013: 75–92. doi: 10.1007/978-3-642-40041-4_5.
[11]	CHILLOTTI I, GAMA N, GEORGIEVA M, et al. TFHE: Fast fully homomorphic encryption over the torus[J]. Journal of Cryptology, 2020, 33(1): 34–91. doi: 10.1007/s00145-019-09319-x.
[12]	BRAKERSKI Z and VAIKUNTANATHAN V. Fully homomorphic encryption from ring-LWE and security for key dependent messages[C]. The 31st Annual Cryptology Conference, Santa Barbara, USA, 2011: 505–524. doi: 10.1007/978-3-642-22792-9_29.
[13]	COSTACHE A and SMART N P. Which ring based somewhat homomorphic encryption scheme is best?[C]. The Cryptographers' Track at the RSA Conference, San Francisco, USA, 2016: 325–340. doi: 10.1007/978-3-319-29485-8_19.
[14]	CHEON J H, HAN K, KIM A, et al. Bootstrapping for approximate homomorphic encryption[C]. The 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, 2018: 360–384. doi: 10.1007/978-3-319-78381-9_14.
[15]	ALPERIN-SHERIFF J and PEIKERT C. Faster bootstrapping with polynomial error[C]. The 34th Annual Cryptology Conference, Santa Barbara, USA, 2014: 297–314. doi: 10.1007/978-3-662-44371-2_17.
[16]	DUCAS L and MICCIANCIO D. FHEW: Bootstrapping homomorphic encryption in less than a second[C]. The 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 2015: 617–640. doi: 10.1007/978-3-662-46800-5_24.
[17]	GAMA N, IZABACHÈNE M, NGUYEN P Q, et al. Structural lattice reduction: Generalized worst-case to average-case reductions and homomorphic cryptosystems[C]. The 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 2016: 528–558. doi: 10.1007/978-3-662-49896-5_19.
[18]	SMART N P and VERCAUTEREN F. Fully homomorphic SIMD operations[J]. Designs, Codes and Cryptography, 2014, 71(1): 57–81. doi: 10.1007/s10623-012-9720-4.
[19]	GARNER H L. The residue number system[C]. The Western Joint Computer Conference, San Francisco, USA, 1959: 146–153. doi: 10.1145/1457838.1457864.
[20]	HALEVI S and SHOUP V. Algorithms in HElib[C]. The 34th Annual Cryptology Conference, Santa Barbara, USA, 2014: 554–571. doi: 10.1007/978-3-662-44371-2_31.
[21]	HALEVI S and SHOUP V. Bootstrapping for HElib[J]. Journal of Cryptology, 2021, 34(1): 7. doi: 10.1007/s00145-020-09368-7.
[22]	HALEVI S and SHOUP V. Faster homomorphic linear transformations in HElib[C]. The 38th Annual International Cryptology Conference, Santa Barbara, USA, 2018: 93–120. doi: 10.1007/978-3-319-96884-1_4.
[23]	JUVEKAR C, VAIKUNTANATHAN V, and CHANDRAKASAN A. GAZELLE: A low latency framework for secure neural network inference[C]. The 27th USENIX Conference on Security Symposium, Baltimore, USA, 2018: 1651–1669.
[24]	BIAN S, KUNDI D E S, HIROZAWA K, et al. APAS: Application-specific accelerators for RLWE-based homomorphic linear transformations[J]. IEEE Transactions on Information Forensics and Security, 2021, 16: 4663–4678. doi: 10.1109/TIFS.2021.3114032.
[25]	BOSSUAT J P, MOUCHET C, TRONCOSO-PASTORIZA J, et al. Efficient bootstrapping for approximate homomorphic encryption with non-sparse keys[C]. The 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 2021: 587–617. doi: 10.1007/978-3-030-77870-5_21.
[26]	LEE Y, LEE J W, KIM Y S, et al. High-precision bootstrapping for approximate homomorphic encryption by error variance minimization[C]. The 41st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 2022: 551–580. doi: 10.1007/978-3-031-06944-4_19.
[27]	JUTLA C S and MANOHAR N. Sine series approximation of the mod function for bootstrapping of approximate HE[C]. The 41st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 2022: 491–520. doi: 10.1007/978-3-031-06944-4_17.
[28]	CHEN Hao, CHILLOTTI I, and SONG Y. Improved bootstrapping for approximate homomorphic encryption[C]. The 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, 2019: 34–54. doi: 10.1007/978-3-030-17656-3_2.
[29]	LEE J W, LEE E, LEE Y, et al. High-precision bootstrapping of RNS-CKKS homomorphic encryption using optimal minimax polynomial approximation and inverse sine function[C]. The 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 2021: 618–647. doi: 10.1007/978-3-030-77870-5_22.
[30]	RATHEE D, RATHEE M, KUMAR N, et al. CrypTFlow2: Practical 2-party secure inference[C]. The 2020 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, USA, 2020: 325–342. doi: 10.1145/3372297.3417274.
[31]	BAJARD J C, EYNARD J, HASAN M A, et al. A full RNS variant of FV like somewhat homomorphic encryption schemes[C]. The 23rd International Conference on Selected Areas in Cryptography, St. John's, Canada, 2017: 423–442. doi: 10.1007/978-3-319-69453-5_23.
[32]	CHEON J H, HAN K, KIM A, et al. A full RNS variant of approximate homomorphic encryption[C]. The 25th International Conference on Selected Areas in Cryptography, Calgary, Canada, 2019: 347–368. doi: 10.1007/978-3-030-10970-7_16.
[33]	HALEVI S, POLYAKOV Y, and SHOUP V. An improved RNS variant of the BFV homomorphic encryption scheme[C]. The Cryptographers’ Track at the RSA Conference, San Francisco, USA, 2019: 83–105. doi: 10.1007/978-3-030-12612-4_5.
[34]	GENTRY C, HALEVI S, and SMART N P. Homomorphic evaluation of the AES circuit[C]. The 32nd Annual Cryptology Conference, Santa Barbara, USA, 2012: 850–867. doi: 10.1007/978-3-642-32009-5_49.
[35]	CHEON J H, HAN K, KIM A, et al. A full RNS variant of approximate homomorphic encryption[C]. The 25th International Conference on Selected Areas in Cryptography, Calgary, Canada, 2019: 347–368. doi: 10.1007/978-3-030-10970-7_16.
[36]	HAN K and KI D. Better bootstrapping for approximate homomorphic encryption[C]. The Cryptographers’ Track at the RSA Conference 2020, San Francisco, USA, 2020: 364–390. doi: 10.1007/978-3-030-40186-3_16.
[37]	KIM A, PAPADIMITRIOU A, and POLYAKOV Y. Approximate homomorphic encryption with reduced approximation error[R]. Cryptology ePrint Archive 2022/1118, 2022: 120–144.
[38]	MICCIANCIO D and POLYAKOV Y. Bootstrapping in FHEW-like cryptosystems[C]. The 9th on Workshop on Encrypted Computing & Applied Homomorphic Cryptography, Seoul, South Korea, 2021: 17–28. doi: 10.1145/3474366.3486924.
[39]	BONNORON G, DUCAS L, and FILLINGER M. Large FHE gates from tensored homomorphic accumulator[C]. The 10th International Conference on Cryptology in Africa, Marrakesh, Morocco, 2018: 217–251. doi: 10.1007/978-3-319-89339-6_13.
[40]	LEE Y, MICCIANCIO D, KIM A, et al. Efficient FHEW bootstrapping with small evaluation keys, and applications to threshold homomorphic encryption[R]. Cryptology ePrint Archive 2022/198, 2022.
[41]	MICCIANCIO D and SORRELL J. Ring packing and amortized FHEW bootstrapping[R]. Cryptology ePrint Archive 2018/532, 2018.
[42]	GUIMARÃES A, PEREIRA H V L, and VAN LEEUWEN B. Amortized bootstrapping revisited: Simpler, asymptotically-faster, implemented[J]. Cryptology ePrint Archive 2023/014, 2023.
[43]	LIU Fenghao and WANG Han. Batch bootstrapping I: A new framework for SIMD bootstrapping in polynomial modulus[C]. The 42nd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Lyon, France, 2023: 321–352. doi: 10.1007/978-3-031-30620-4_11.
[44]	BOURA C, GAMA N, GEORGIEVA M, et al. Simulating homomorphic evaluation of deep learning predictions[C]. The 3rd International Symposium on Cyber Security Cryptography and Machine Learning, Beer-Sheva, Israel, 2019: 212–230. doi: 10.1007/978-3-030-20951-3_20.
[45]	CHILLOTTI I, JOYE M, and PAILLIER P. Programmable bootstrapping enables efficient homomorphic inference of deep neural networks[C]. The 5th International Symposium on Cyber Security Cryptography and Machine Learning, Be’er Sheva, Israel, 2021: 1–19. doi: 10.1007/978-3-030-78086-9_1.
[46]	CLET P E, ZUBER M, BOUDGUIGA A, et al. Putting up the swiss army knife of homomorphic calculations by means of TFHE functional bootstrapping[R]. Cryptology ePrint Archive 2022/149, 2022.
[47]	KLUCZNIAK K and SCHILD L. FDFB: Full domain functional bootstrapping towards practical fully homomorphic encryption[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2022, 2023(1): 501–537. doi: 10.46586/tches.v2023.i1.501-537.
[48]	YANG Zhaomin, XIE Xiang, SHEN Huajie, et al. TOTA: Fully homomorphic encryption with smaller parameters and stronger security[R]. Cryptology ePrint Archive, 2021/1347, 2021.
[49]	CARPOV S, GAMA N, GEORGIEVA M, et al. Privacy-preserving semi-parallel logistic regression training with fully homomorphic encryption[J]. BMC Medical Genomics, 2020, 13(7): 88. doi: 10.1186/s12920-020-0723-0.
[50]	GUIMARÃES A, BORIN E, and ARANHA D F. Revisiting the functional bootstrap in TFHE[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 2021(2): 229–253. doi: 10.46586/tches.v2021.i2.229-253.
[51]	CHILLOTTI I, LIGIER D, ORFILA J B, et al. Improved programmable bootstrapping with larger precision and efficient arithmetic circuits for TFHE[C]. The 27th International Conference on the Theory and Application of Cryptology and Information Security, Singapore, 2021: 670–699. doi: 10.1007/978-3-030-92078-4_23.
[52]	CHEN Hao, CHILLOTTI I, and SONG Y. Multi-key homomorphic encryption from TFHE[C]. The 25th International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, 2019: 446–472. doi: 10.1007/978-3-030-34621-8_16.
[53]	BOURA C, GAMA N, GEORGIEVA M, et al. CHIMERA: Combining ring-LWE-based fully homomorphic encryption schemes[J]. Journal of Mathematical Cryptology, 2020, 14(1): 316–338. doi: 10.1515/jmc-2019-0026.
[54]	CHEN Hao, DAI Wei, KIM M, et al. Efficient homomorphic conversion between (ring) LWE ciphertexts[C]. The 19th International Conference on Applied Cryptography and Network Security, Kamakura, Japan, 2021: 460–479. doi: 10.1007/978-3-030-78372-3_18.
[55]	REN Xuanle, SU Le, GU Zhen, et al. HEDA: Multi-attribute unbounded aggregation over homomorphically encrypted database[J]. Proceedings of the VLDB Endowment, 2022, 16(4): 601–614. doi: 10.14778/3574245.3574248.
[56]	GÖTTERT N, FELLER T, SCHNEIDER M, et al. On the design of hardware building blocks for modern lattice-based encryption schemes[C]. The 14th International Workshop on Cryptographic Hardware and Embedded Systems, Leuven, Belgium, 2012: 512–529. doi: 10.1007/978-3-642-33027-8_30.
[57]	PÖPPELMANN T and GÜNEYSU T. Towards efficient arithmetic for lattice-based cryptography on reconfigurable hardware[C]. The 2nd International Conference on Cryptology and Information Security in Latin America, Santiago, Chile, 2012: 139–158. doi: 10.1007/978-3-642-33481-8_8.
[58]	PÖPPELMANN T and GÜNEYSU T. Towards practical lattice-based public-key encryption on reconfigurable hardware[C]. The 20th International Conference on Selected Areas in Cryptography, Burnaby, Canada, 2014: 68–85. doi: 10.1007/978-3-662-43414-7_4.
[59]	施佺, 韩赛飞, 黄新明, 等. 面向全同态加密的有限域FFT算法FPGA设计[J]. 电子与信息学报, 2018, 40(1): 57–62. doi: 10.11999/JEIT170312. SHI Quan, HAN Saifei, HUANG Xinming, et al. Design of finite field FFT for fully homomorphic encryption based on FPGA[J]. Journal of Electronics & Information Technology, 2018, 40(1): 57–62. doi: 10.11999/JEIT170312.
[60]	RIAZI M S, LAINE K, PELTON B, et al. HEAX: An architecture for computing on encrypted data[C]. The Twenty-Fifth International Conference on Architectural Support for Programming Languages and Operating Systems, Lausanne, Switzerland, 2020: 1295–1309. doi: 10.1145/3373376.3378523.
[61]	REAGEN B, CHOI W S, KO Y, et al. Cheetah: Optimizing and accelerating homomorphic encryption for private inference[C]. The 2021 IEEE International Symposium on High-Performance Computer Architecture, Seoul, South Korea, 2021: 26–39. doi: 10.1109/HPCA51647.2021.00013.
[62]	SAMARDZIC N, FELDMANN A, KRASTEV A, et al. F1: A fast and programmable accelerator for fully homomorphic encryption[C]. The 54th Annual IEEE/ACM International Symposium on Microarchitecture, Greece, 2021: 238–252. doi: 10.1145/3466752.3480070.
[63]	SAMARDZIC N, FELDMANN A, KRASTEV A, et al. CraterLake: A hardware accelerator for efficient unbounded computation on encrypted data[C]. The 49th Annual International Symposium on Computer Architecture, New York, USA, 2022: 173–187. doi: 10.1145/3470496.3527393.
[64]	KIM J, LEE G, KIM S, et al. ARK: Fully homomorphic encryption accelerator with runtime data generation and inter-operation key reuse[C]. The 2022 55th IEEE/ACM International Symposium on Microarchitecture, Chicago, USA, 2022: 1237–1254. doi: 10.1109/MICRO56248.2022.00086.
[65]	JUNG W, KIM S, AHN J H, et al. Over 100x faster bootstrapping in fully homomorphic encryption through memory-centric optimization with GPUs[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 2021(4): 114–148. doi: 10.46586/tches.v2021.i4.114-148.
[66]	YANG Yinghao, ZHANG Huaizhi, FAN Shengyu, et al. Poseidon: Practical homomorphic encryption accelerator[C]. 2023 IEEE International Symposium on High-Performance Computer Architecture, Montreal, Canada, 2023: 870–881. doi: 10.1109/HPCA56546.2023.10070984.
[67]	ZHU Yilan, WANG Xinyao, JU Lei, et al. FxHENN: FPGA-based acceleration framework for homomorphic encrypted CNN inference[C]. 2023 IEEE International Symposium on High-Performance Computer Architecture, Montreal, Canada, 2023: 896–907. doi: 10.1109/HPCA56546.2023.10071133.
[68]	BRUTZKUS A, GILAD-BACHRACH R, and ELISHA O. Low latency privacy preserving inference[C]. The 36th International Conference on Machine Learning, Long Beach, USA, 2019: 812–821.
[69]	FAN Shengyu, WANG Zhiwei, XU Weizhi, et al. TensorFHE: Achieving practical computation on encrypted data using GPGPU[C]. 2023 IEEE International Symposium on High-Performance Computer Architecture, Montreal, Canada, 2023: 922–934. doi: 10.1109/HPCA56546.2023.10071017.
[70]	JIANG Lei, LOU Qian, and JOSHI N. MATCHA: A fast and energy-efficient accelerator for fully homomorphic encryption over the torus[C]. The 59th ACM/IEEE Design Automation Conference, San Francisco, USA, 2022: 235–240. doi: 3489517.3530435.
[71]	DAI Wei. CUDA-accelerated fully homomorphic encryption library[EB/OL]. https://github.com/vernamlab/cuFHE, 2023.
[72]	GENER Y S, NEWTON P, TAN D, et al. An FPGA-based programmable vector engine for fast fully homomorphic encryption over the torus[EB/OL]. https://people.ece.ubc.ca/lemieux/publications/gener-spsl2021.pdf, 2021.
[73]	VAN BEIRENDONCK M, D'ANVERS J P, TURAN F, et al. FPT: A fixed-point accelerator for torus fully homomorphic encryption[C]. The 2023 ACM SIGSAC Conference on Computer and Communications Security, Copenhagen, Denmark, 2023: 741–755. doi: 10.1145/3576915.3623159.
[74]	YE Tian, KANNAN R, and PRASANNA V K. FPGA acceleration of fully homomorphic encryption over the torus[C]. 2022 IEEE High Performance Extreme Computing Conference, Waltham, USA, 2022: 1–7. doi: 10.1109/HPEC55821.2022.9926381.
[75]	AL BADAWI A, POLYAKOV Y, AUNG K M M, et al. Implementation and performance evaluation of RNS variants of the BFV homomorphic encryption scheme[J]. IEEE Transactions on Emerging Topics in Computing, 2021, 9(2): 941–956. doi: 10.1109/TETC.2019.2902799.
[76]	AL BADAWI A, JIN Chao, LIN Jie, et al. Towards the AlexNet moment for homomorphic encryption: HCNN, the first homomorphic CNN on encrypted data with GPUs[J]. IEEE Transactions on Emerging Topics in Computing, 2021, 9(3): 1330–1343. doi: 10.1109/TETC.2020.3014636.
[77]	DAI W and SUNAR B. cuHE: A homomorphic encryption accelerator library[C]. The 2nd International Conference on Cryptography and Information Security in the Balkans, Koper, Slovenia, 2016: 169–186. doi: 10.1007/978-3-319-29172-7_11.
[78]	AL BADAWI A, VEERAVALLI B, MUN C F, et al. High-performance FV somewhat homomorphic encryption on GPUs: An implementation using CUDA[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2018, 2018(2): 70–95. doi: 10.13154/tches.v2018.i2.70-95.
[79]	ÖZERK Ö, ELGEZEN C, MERT A C, et al. Efficient number theoretic transform implementation on GPU for homomorphic encryption[J]. The Journal of Supercomputing, 2022, 78(2): 2840–2872. doi: 10.1007/s11227-021-03980-5.
[80]	MORSHED T, AL AZIZ M, and MOHAMMED N. CPU and GPU accelerated fully homomorphic encryption[C]. 2020 IEEE International Symposium on Hardware Oriented Security and Trust, San Jose, USA, 2020: 142–153. doi: 10.1109/HOST45689.2020.9300288.

施引文献

期刊类型引用(4)

1.	李贵勇，贾璐，宋利利. 宽带太赫兹大规模MIMO系统中的混合预编码. 重庆邮电大学学报(自然科学版). 2024(02): 220-228 . 百度学术
2.	叶子绿，许魁，夏晓晨，邓诚，魏琛，谢威. 基于强化学习的STAR-RIS辅助的通信抗干扰方法. 移动通信. 2024(06): 69-74 . 百度学术
3.	江浩，石旺旗，朱秋明，束锋，WANG Jiangzhou. 面向6G可重构智能超表面使能的近场海洋通信信道建模与信号传播机理研究. 电子与信息学报. 2024(12): 4383-4390 . 本站查看
4.	孙艺玮，顾琪，苏鑫，王菡凝，袁弋非. 可重构智能表面与网络控制中继器的性能比较. 移动通信. 2023(11): 33-38 . 百度学术

其他类型引用(2)

资源附件(0)

访问统计

图(8) / 表(4)

计量

文章访问数: 2138
HTML全文浏览量: 1015
PDF下载量: 464
被引次数: 6

1. 引言
2. 问题模型
2.1 时分复用技术
2.2 FPGA间的布线问题
3. 总体框架
3.1 布线拓扑生成
3.2 TDM比率分配
3.3 TDM比率优化
3.4 多线程并行化
4. 实验结果
4.1 与ALIFRouter及MSFRoute的实验比较
4.2 多线程并行化方法的有效性验证
4.3 自适应布线算法有效性验证
4.4 LR分配算法和TDM比率优化算法有效性验证
5. 结束语

1. 引言
2. 问题模型
2.1 时分复用技术
2.2 FPGA间的布线问题
3. 总体框架
3.1 布线拓扑生成
3.2 TDM比率分配
3.3 TDM比率优化
3.4 多线程并行化
4. 实验结果
4.1 与ALIFRouter及MSFRoute的实验比较
4.2 多线程并行化方法的有效性验证
4.3 自适应布线算法有效性验证
4.4 LR分配算法和TDM比率优化算法有效性验证
5. 结束语

参考文献(80)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

全同态加密软硬件加速研究进展

doi: 10.11999/JEIT230448

通讯作者:
董进　dongjin@baec.org.cn

关振宇　guanzhenyu@buaa.edu.cn

计量

A Survey on Software-hardware Acceleration for Fully Homomorphic Encryption

1. 引言

2. 问题模型

2.1 时分复用技术

2.2 FPGA间的布线问题

3. 总体框架

3.1 布线拓扑生成

3.2 TDM比率分配

3.3 TDM比率优化

3.4 多线程并行化

4. 实验结果

4.1 与ALIFRouter及MSFRoute的实验比较

4.2 多线程并行化方法的有效性验证

4.3 自适应布线算法有效性验证

4.4 LR分配算法和TDM比率优化算法有效性验证

5. 结束语

期刊类型引用(4)

其他类型引用(2)

计量

目录

1. 引言

2. 问题模型

2.1 时分复用技术

2.2 FPGA间的布线问题

3. 总体框架

3.1 布线拓扑生成

3.2 TDM比率分配

3.3 TDM比率优化

3.4 多线程并行化

4. 实验结果

4.1 与ALIFRouter及MSFRoute的实验比较

4.2 多线程并行化方法的有效性验证

4.3 自适应布线算法有效性验证

4.4 LR分配算法和TDM比率优化算法有效性验证

5. 结束语

留言板

全同态加密软硬件加速研究进展

doi: 10.11999/JEIT230448

通讯作者: 董进 dongjin@baec.org.cn 关振宇 guanzhenyu@buaa.edu.cn

计量

出版历程

A Survey on Software-hardware Acceleration for Fully Homomorphic Encryption

1. 引言

2. 问题模型

2.1 时分复用技术

2.2 FPGA间的布线问题

3. 总体框架

3.1 布线拓扑生成

3.2 TDM比率分配

3.3 TDM比率优化

3.4 多线程并行化

4. 实验结果

4.1 与ALIFRouter及MSFRoute的实验比较

4.2 多线程并行化方法的有效性验证

4.3 自适应布线算法有效性验证

4.4 LR分配算法和TDM比率优化算法有效性验证

5. 结束语

期刊类型引用(4)

其他类型引用(2)

计量

出版历程

目录

1. 引言

2. 问题模型

2.1 时分复用技术

2.2 FPGA间的布线问题

3. 总体框架

3.1 布线拓扑生成

3.2 TDM比率分配

3.3 TDM比率优化

3.4 多线程并行化

4. 实验结果

4.1 与ALIFRouter及MSFRoute的实验比较

4.2 多线程并行化方法的有效性验证

4.3 自适应布线算法有效性验证

4.4 LR分配算法和TDM比率优化算法有效性验证

5. 结束语

通讯作者:
董进　dongjin@baec.org.cn

关振宇　guanzhenyu@buaa.edu.cn