Underwater Bearing-only Passive Target Tracking Method Based on Area of Uncertainty
-
摘要: 围绕水下被动目标跟踪问题,目前的研究通常以最优估计点迹表征被测目标跟踪状态,而点估计无法表达示向性的位置误差信息,导致无法较好地为实际战场提供决策支持。针对上述问题,该文提出一种基于不确定区域(AOU)的水下纯方位目标跟踪方案。首先,提出一种基于变权解析的定位算法以获得精确的目标位置信息,将目标位置作为AOU构建算法的先验知识。然后,分别通过有无滤波不确定区域构造算法,输出目标位置不确定区域。通过对不同仿真态势下AOU的评估指标进行统计分析,结果表明利用该目标跟踪方案均能对目标实现可靠精确的位置估计,说明该文提出的基于不确定区域的目标跟踪方案能够有效完成目标跟踪任务。该方案优势在于,目标估计结果包含示向性位置误差和区间估计的置信度,为后续决策提供清晰的容错与判断区域,具有更好的参考价值及实用价值。Abstract: Considering the underwater acoustic bearings-only passive localization, the current research usually uses the optimal estimation point trace to represent the tracking state of the measured target, but point estimation cannot express directional position error information, resulting in the inability to provide better decision support for the actual battlefield. In view of the above problems, bearing-only underwater target tracking scheme based on Area Of Uncertainty (AOU) containing spatial error information is proposed. Firstly, localization algorithm based on variable weighting analysis is introduced to obtain accurate target position information. The target position is then used as prior knowledge for the AOU construction algorithm. Subsequently, the algorithms for constructing uncertain regions with and without filtering are employed to output the target's position uncertainty area. By statistically analyzing the evaluation metrics of the AOU under different simulation scenarios, the results demonstrate that the target tracking scheme based on AOU can reliably and accurately estimate the target position. It indicates that the proposed target tracking scheme based on uncertain regions can effectively fulfill the task of target tracking, the advantage of this approach lies that the target estimation results include directional position errors and confidence intervals for interval estimation. this provides clear fault-tolerant and judgment regions for subsequent decision-making, This offers enhanced reference value and practical value.
-
表 1 旋转角$\beta $的符号确定原则
B A > C A = C A < C B>0 $\beta + {\pi}/2$ $ {\pi}/4 $ $\beta $ B=0 $ {\pi}/2 $ / 0 B<0 $\beta - {\pi}/2$ –$ {\pi}/4 $ $\beta $ 表 2 仿真参数
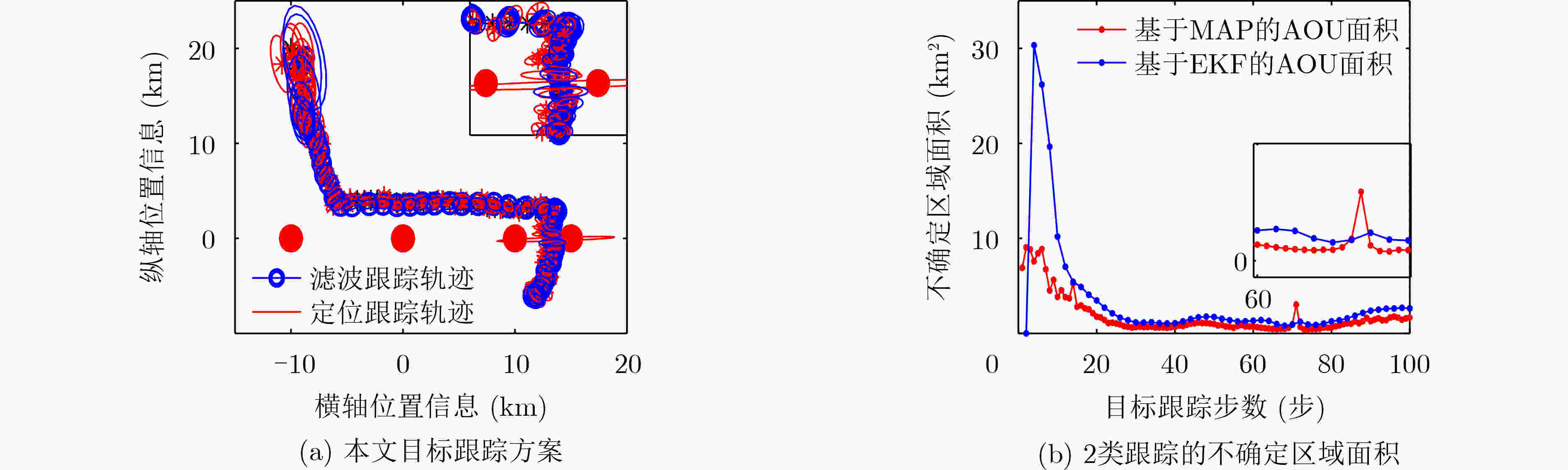
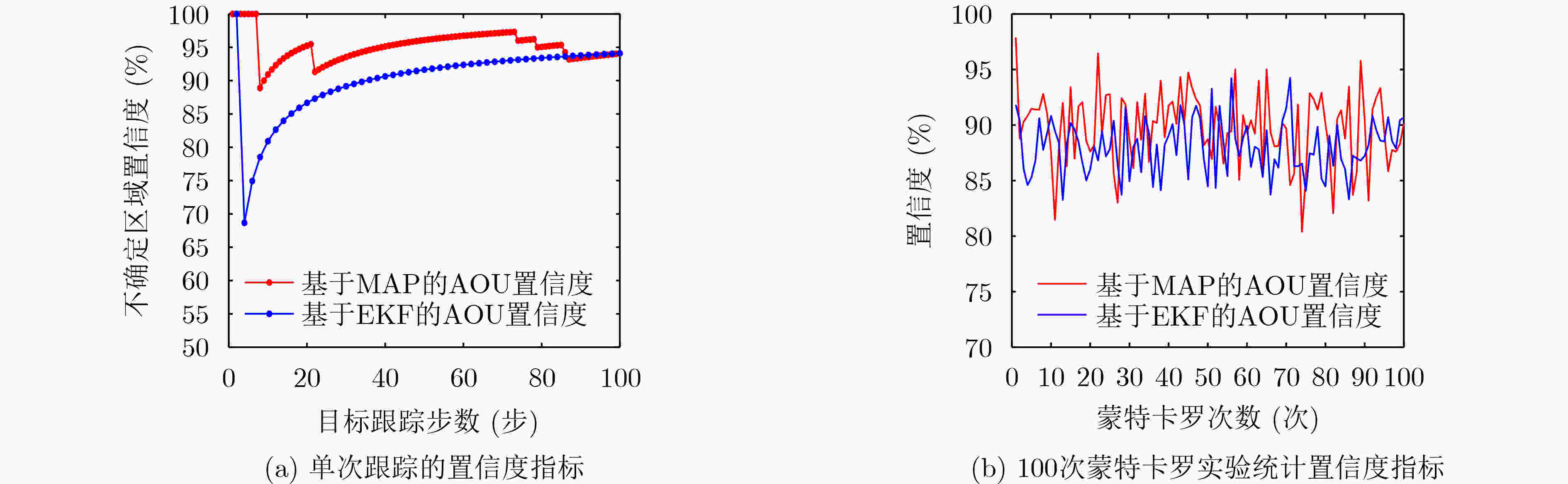
参数 名称 数值 ${{\boldsymbol{X}}_0}$ 目标初始状态向量 $\left( { - 10,20,0.2, - 0.5} \right)$ ${\sigma _\theta }$ 平台量测误差 $\left( {1^\circ ,2^\circ ,2^\circ ,3^\circ } \right)$ ${X_P}$ 平台位置信息(km) $( - 10,0),(0,0),(10,0),(15,0)$ ${ { {T} }_{ {\text{p} } } }$ 定位采样间隔(s) 1 ${ { {T} }_{ {\text{t} } } }$ 滤波采样间隔(s) 2 $\Delta {\boldsymbol{v}}$ 变向速度状态向量 ${\left( {0.2, - 0.5} \right)_{ {\text{ini} } } } \to {\left( {0.5,0} \right)_{30\;{\text{s} } } } \to {\left( { - 0.1, - 0.3} \right)_{60\;{\text{s} } } }$ 表 3 仿真参数
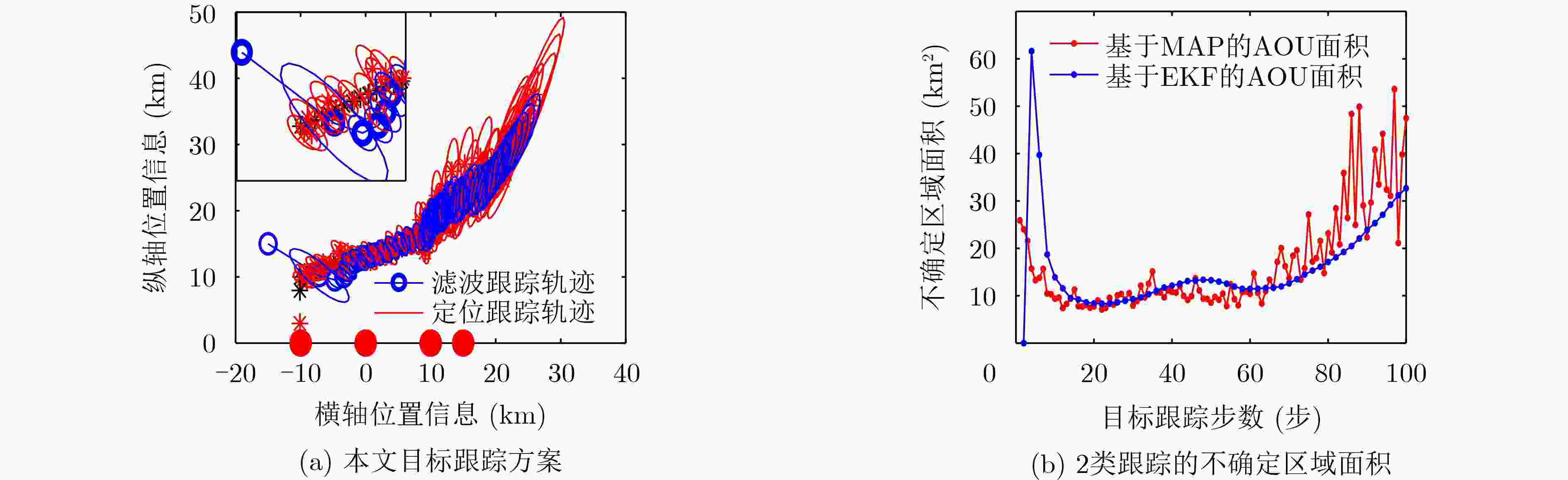
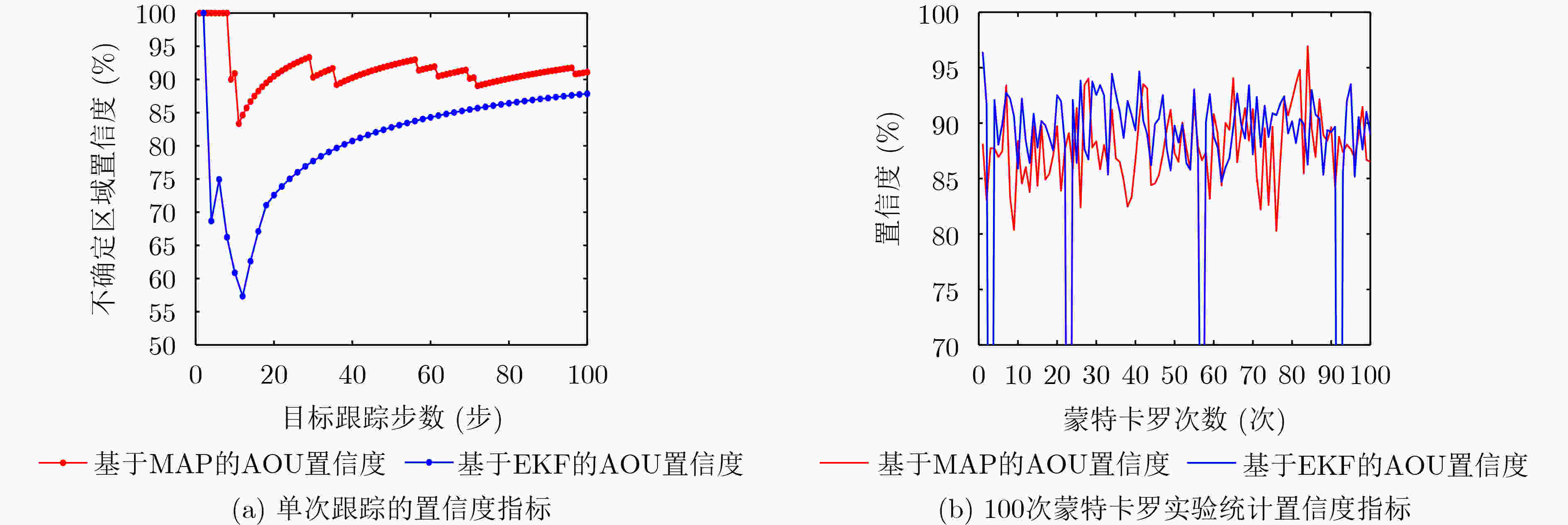
参数 名称 数值 ${{\boldsymbol{X}}_0}$ 目标初始状态向量 $\left( { - 10,10,0.6,0.2} \right)$ ${\sigma _\theta }$ 平台量测误差 $\left( {3^\circ ,2^\circ ,2^\circ ,1^\circ } \right)$ ${X_P}$ 平台位置信息(km) $( - 10,0),(0,0),(10,0),(15,0)$ ${ { {T} }_{ {\text{p} } } }$ 定位采样间隔(s) 1 ${ { {T} }_{ {\text{t} } } }$ 滤波采样间隔(s) 2 $\Delta {\boldsymbol{v}}$ 变向速度状态向量 ${\left( {0.6,0.2} \right)_{ {\text{ini} } } } \to {\left( {0,0.3} \right)_{30\;{\text{s} } } } \to {\left( {0.3,0.2} \right)_{60\;{\text{s} } } }$ -
[1] 杨文生, 吴旭. 非线性约束条件下的双阵纯方位目标运动分析[J]. 舰船科学技术, 2022, 44(13): 149–152. doi: 10.3404/j.issn.1672-7649.2022.13.032YANG Wensheng and WU Xu. Bearings-only target motion analysis with nonlinear inequality constraints using two arrays[J]. Ship Science and Technology, 2022, 44(13): 149–152. doi: 10.3404/j.issn.1672-7649.2022.13.032 [2] 苏钰. 单基阵纯方位水下目标运动分析技术研究[D]. [硕士论文], 哈尔滨工程大学, 2021.SU Yu. Underwater target motion analysis technology with single base array bearing-only[D]. [Master dissertation], Harbin Engineering University, 2021. [3] JIANG Cuicui, FANG Yizhong, and HU Qinglei. Motion prediction for target tracking with bearing-only measurement[C]. 2022 41st Chinese Control Conference (CCC), Hefei, China, 2022: 3415–3420. [4] 王本才, 王国宏, 何友. 多站纯方位无源定位算法研究进展[J]. 电光与控制, 2012, 19(5): 56–62. doi: 10.3969/j.issn.1671-637X.2012.05.013WANG Bencai, WANG Guohong, and HE You. Progress of research on multi-sensor bearing-only passive locating algorithm[J]. Electro Optics &Control, 2012, 19(5): 56–62. doi: 10.3969/j.issn.1671-637X.2012.05.013 [5] DOĞANÇAY K. Bearings-only target localization using total least squares[J]. Signal Process, 2005, 85(9): 1695–1710. doi: 10.1016/j.sigpro.2005.03.007 [6] 杜金香, 许恒博, 祝鹏. 一种角度加权的最小二乘目标定位算法[J]. 水下无人系统学报, 2019, 27(5): 570–573. doi: 10.11993/j.issn.2096-3920.2019.05.013DU Jinxiang, XU Hengbo, and ZHU Peng. An angle weighted least squares algorithm for target localization[J]. Journal of Unmanned Undersea Systems, 2019, 27(5): 570–573. doi: 10.11993/j.issn.2096-3920.2019.05.013 [7] 王燕, 苏钰, 齐滨, 等. 单基阵三维纯方位水下信标声学定位方法[J]. 声学学报, 2021, 46(3): 375–386. doi: 10.15949/j.cnki.0371-0025.2021.03.006WANG Yan, SU Yu, QI Bin, et al. 3D bearing-only acoustic positioning method for underwater beacon[J]. Acta Acustica, 2021, 46(3): 375–386. doi: 10.15949/j.cnki.0371-0025.2021.03.006 [8] WANG Ding, ZHANG Li, and WU Ying. Constrained total least squares algorithm for passive location based on bearing-only measurements[J]. Science in China Series F:Information Sciences, 2007, 50(4): 576–586. doi: 10.1007/s11432-007-0023-8 [9] 胡宁, 吴华, 王星, 等. 双机交叉定位误差及配置距离最优化协调分析[J]. 火力与指挥控制, 2013, 38(1): 40–44. doi: 10.3969/j.issn.1002-0640.2013.01.011HU Ning, WU Hua, WANG Xing, et al. Location error of bearing crossing location by two aircrafts and analysis of coordination on optimal allocation[J]. Fire Control &Command Control, 2013, 38(1): 40–44. doi: 10.3969/j.issn.1002-0640.2013.01.011 [10] 刁联旺, 张桂林, 王惠娟. 基于广义内心的4站纯方位交叉定位算法[J]. 指挥信息系统与技术, 2014, 5(6): 56–59. doi: 10.15908/j.cnki.cist.2014.06.011DIAO Lianwang, ZHANG Guilin, and WANG Huijuan. 4 station based on generalized inner bearing cross localization algorithm[J]. Journal of Command Information System and Technology, 2014, 5(6): 56–59. doi: 10.15908/j.cnki.cist.2014.06.011 [11] TERAMOTO A, TSUKAMOTO T, KIRIYAMA Y, et al. Automated classification of lung cancer types from cytological images using deep convolutional neural networks[J]. BioMed Research International, 2017, 2017 4067832. [12] 邱硕丰, 刘军. 无源双站交叉定位误差分析[J]. 舰船电子对抗, 2018, 41(5): 22–26. doi: 10.16426/j.cnki.jcdzdk.2018.05.005QIU Shuofeng and LIU Jun. Error analysis for passive double-station cross location[J]. Ship Electronic Countermeasure, 2018, 41(5): 22–26. doi: 10.16426/j.cnki.jcdzdk.2018.05.005 [13] 王洪迅, 弥小溪, 皇甫惠栋, 等. 交叉定位模糊区的精确几何分析[J]. 电光与控制, 2012, 19(3): 17–20. doi: 10.3969/j.issn.1671-637X.2012.03.004WANG Hongxun, MI Xiaoxi, HAUNGFU Huidong, et al. Precise geometrical analysis of Ambiguous area in beam-crossing locating[J]. Electro Optics &Control, 2012, 19(3): 17–20. doi: 10.3969/j.issn.1671-637X.2012.03.004 [14] PARADOWSKI L R. Uncertainty ellipses and their application to interval estimation of emitter position[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(1): 126–133. doi: 10.1109/7.570715 [15] 范胜召, 罗江, 张玥. 概率误差椭圆计算的推导与仿真[J]. 电子信息对抗技术, 2021, 36(6): 50–53. doi: 10.3969/j.issn.1674-2230.2021.06.010FAN Shengzhao, LUO Jiang, and ZHANG Yue. Derivation and simulation of elliptical error probable calculation[J]. Electronic Information Warfare Technology, 2021, 36(6): 50–53. doi: 10.3969/j.issn.1674-2230.2021.06.010 -






 下载:
下载:


 下载:
下载:
