An Efficient and High-precision Power Consumption Prediction Model for the Register Transfer Level Design Phase
-
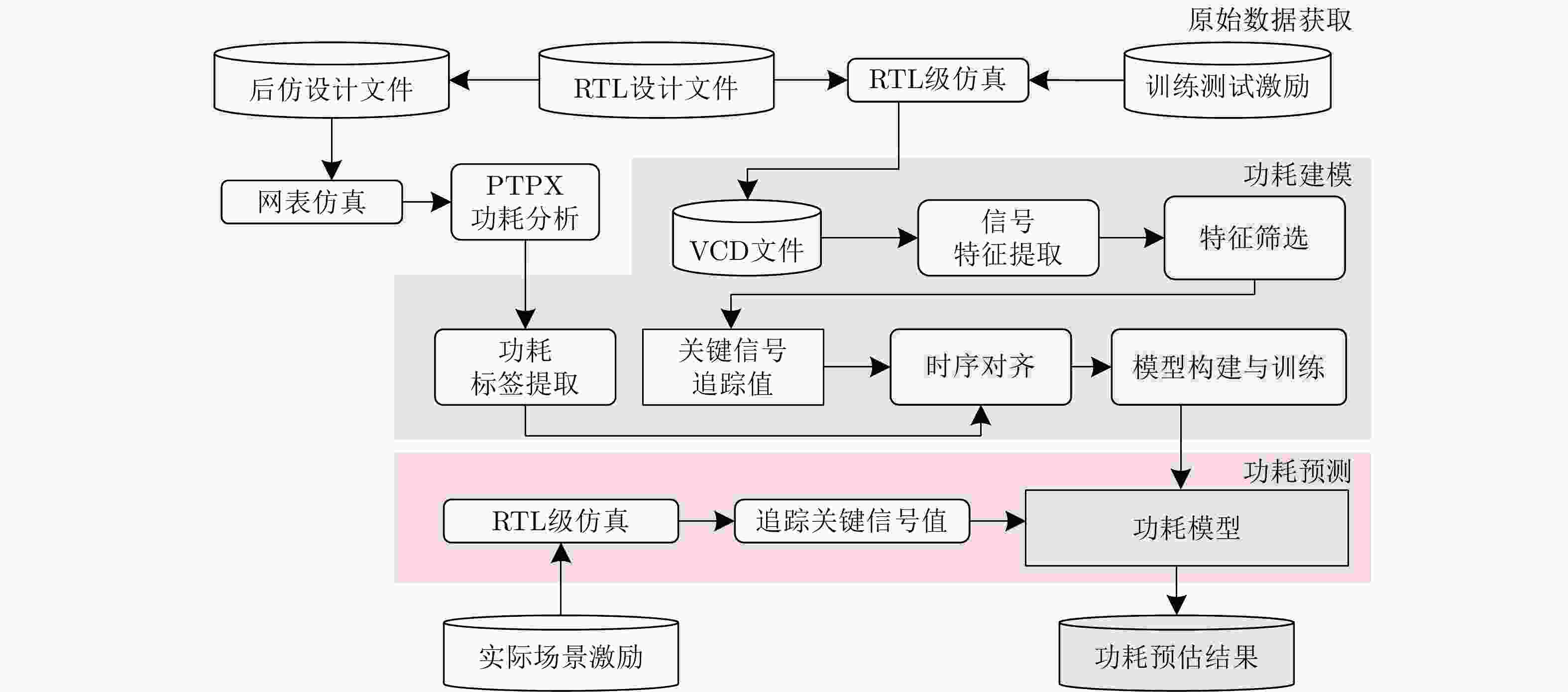
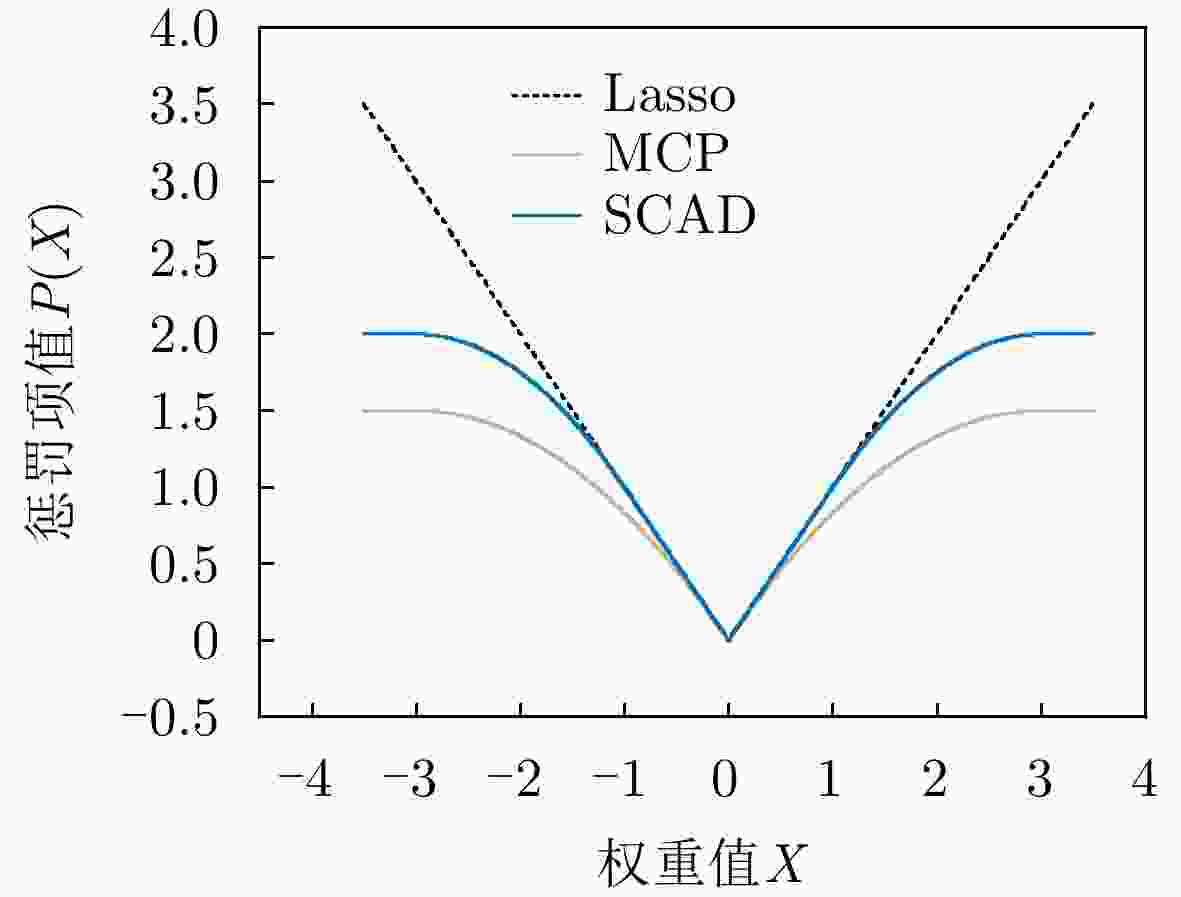
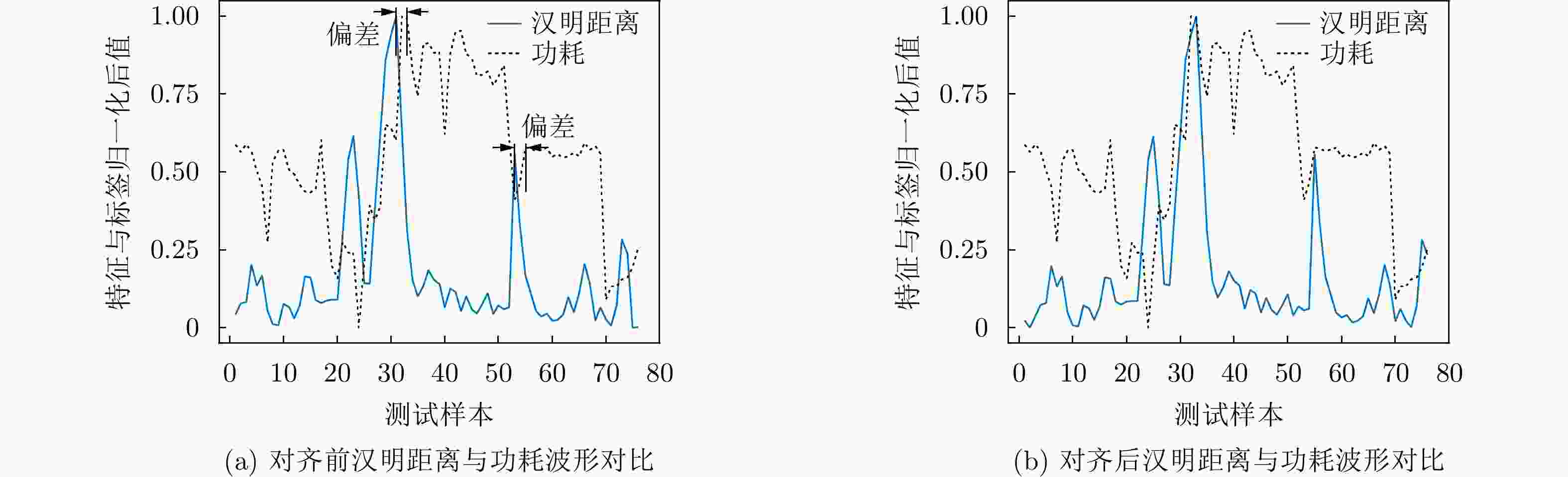
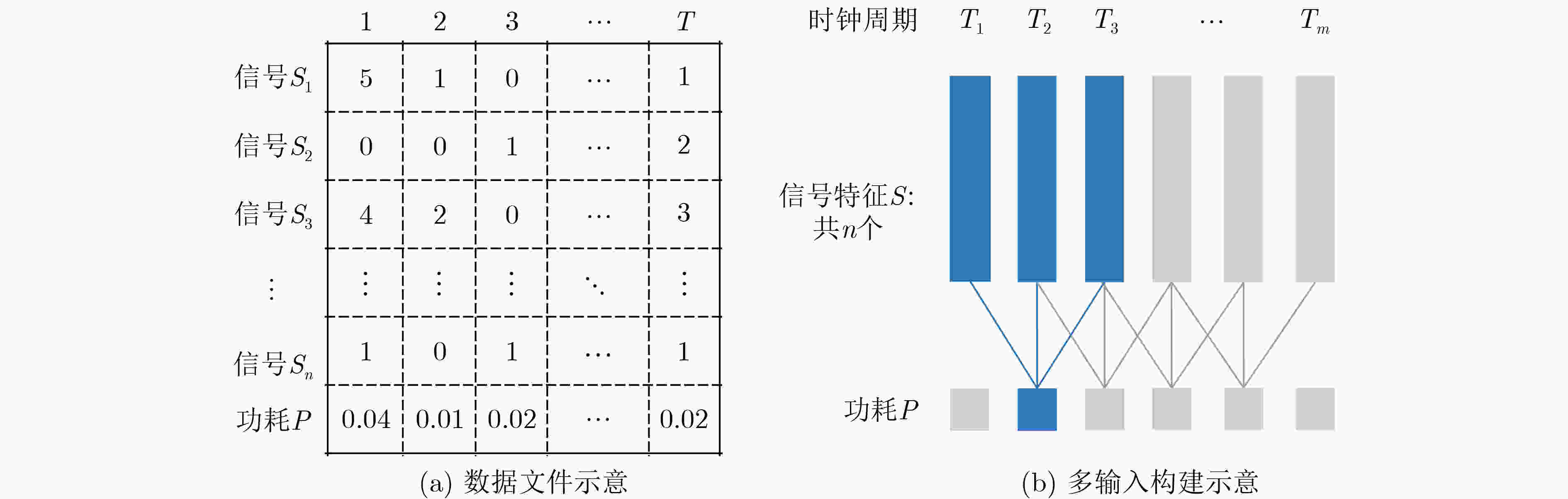
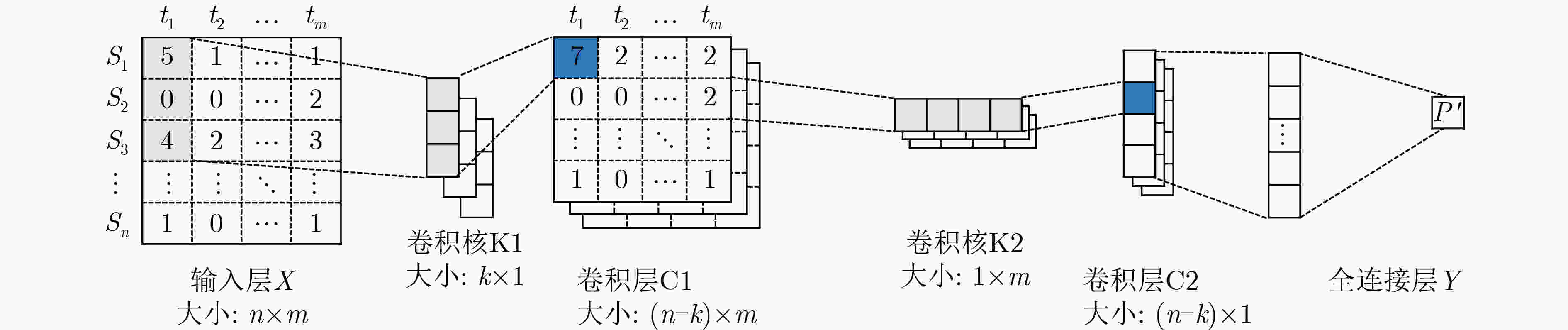
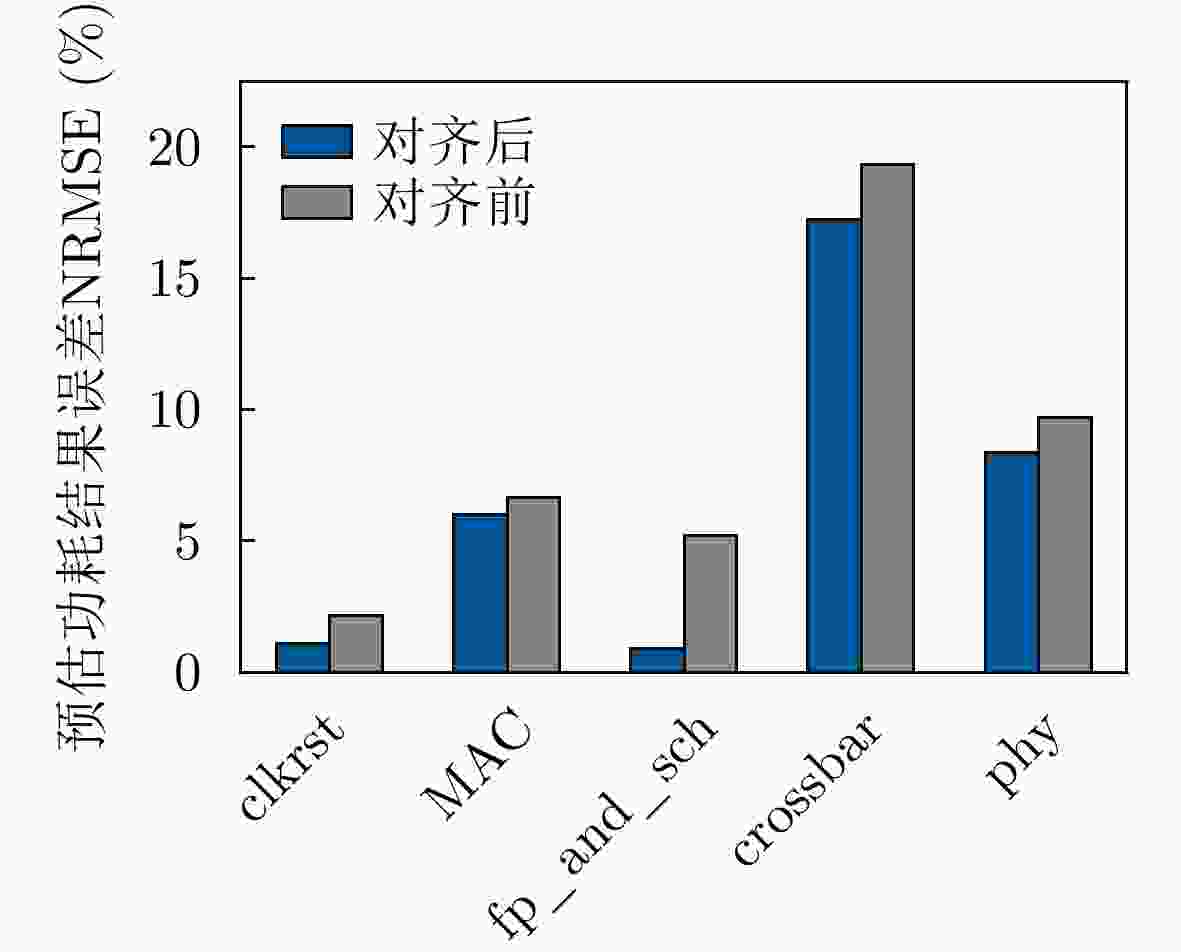
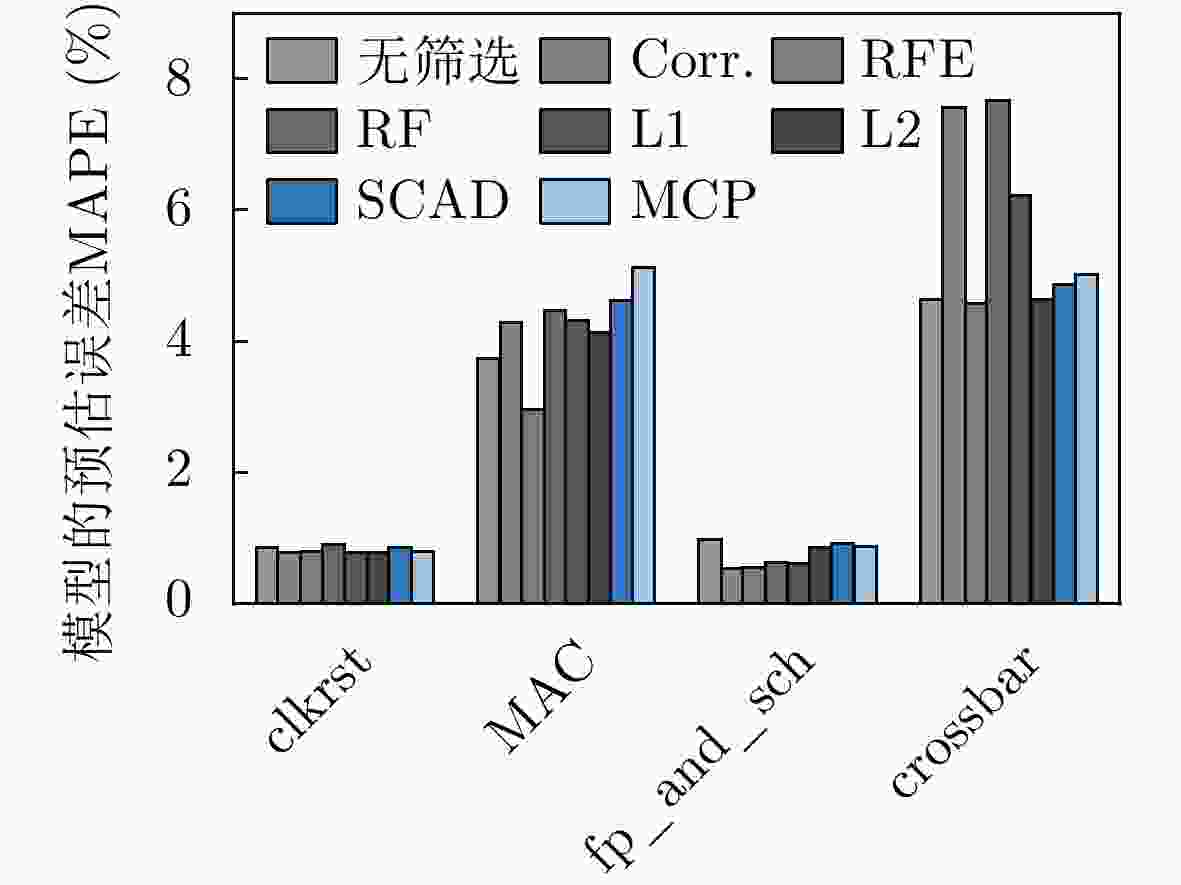
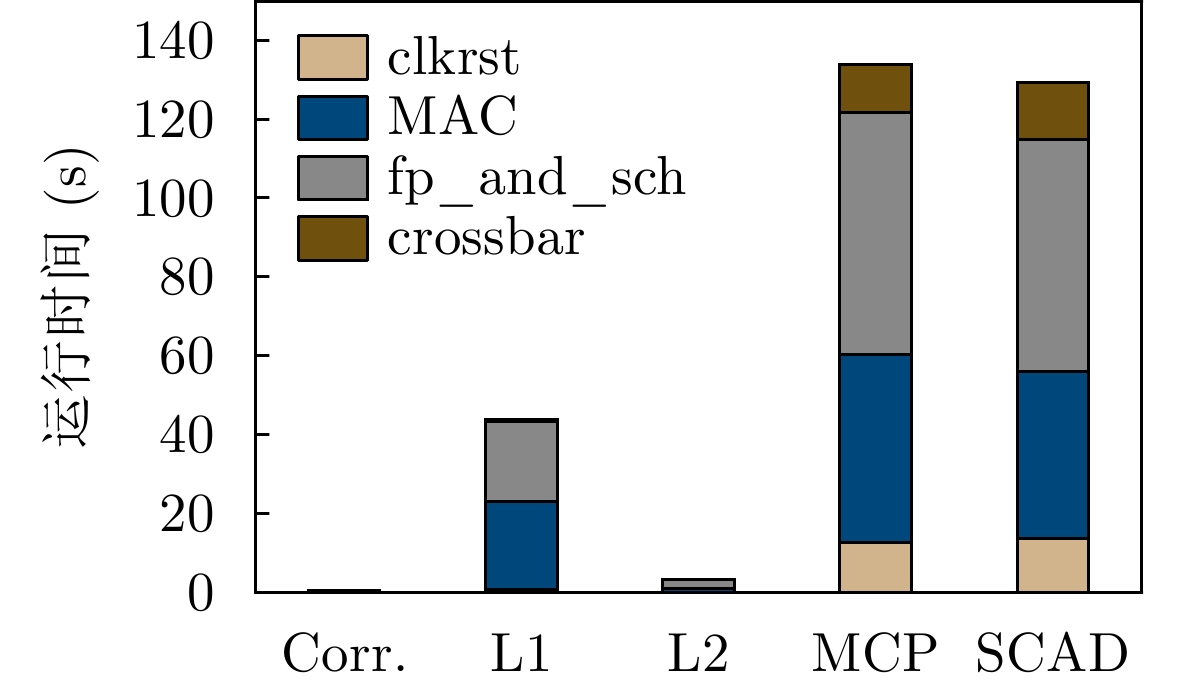
摘要: 功耗已成为电路设计的关键性能目标之一,现有商业工具PrimeTime PX(PTPX)的功耗预精度高,但是运行时间长,且仅面向已经生成网表的逻辑综合或者物理实现阶段。因此,降低功耗分析时间,且前移功耗预测在芯片设计中的环节变得尤为重要。该文提出一种面向千万门级专用集成电路(ASIC)的寄存器传输级(RTL)功耗预估方法,可在RTL设计阶段实现快速且准确的周期级功耗预测:根据输入信号的功耗相关性原则使用基于平滑截断绝对偏差惩罚项(SCAD)的嵌入法对输入信号自动筛选,从而解决大信号特征输入数量对预估性能的影响;通过时序对准方法对仿真波形数据进行校正,解决了sign-off级功耗与RTL级仿真波形之间的时序偏差问题,有效提升了模型预测的精度;建立了仅拥有两个卷积层和1个全连接层的浅层卷积神经网络模型,学习相邻位置和相邻时间上的信号活动与功耗的相关性信息,充分降低部署开销,使训练速度得到显著提高。该文使用开源数据集、28 nm工艺节点的3×107门级工业级芯片电路作为测试对象,实验结果表明,功耗预测结果和物理设计后PTPX分析结果相比,平均绝对百分比误差(MAPE)小于1.71%,11k时钟周期的功耗曲线预测耗时不到1.2 s。在场景交叉验证实验中,模型的预测误差小于4.5%。Abstract: Power consumption is identified as a critical performance objective in circuit design.Existing power estimation tools, such as PrimeTime PX (PTPX), provide high accuracy but are hampered by lengthy execution times and are confined to logic synthesis or physical implementation stages with an already generated netlist. As a result, the need to reduce power analysis time and stress the importance of forward power prediction in chip design has been recognized. A power estimation model for early-stage large-scale Application Specific Integrated Circuit (ASIC) is introduced, which can achieve fast and accurate cycle-level power prediction at the Register Transfer Level (RTL) design stage. The model applies the Smoothly Clipped Absolute Deviation (SCAD) embedding method based on the power correlation principle of input signals for automatic signal selection, addressing the impact of large input feature numbers on estimation performance. A timing alignment method is employed to correct the timing deviation between sign-off level power and RTL-level simulation waveform, enhancing prediction accuracy. The strong nonlinearity of a shallow two-layer convolutional neural network is utilized by the model for power training, consisting of two convolutional layers and one fully connected layer, which reduces computational overhead. Power labels use backend Sign-off level power output data to enhance the accuracy of prediction results.This power estimation model is evaluated on a 28 nm Network Processor(NP) with more than 30 million gates. Experimental results demonstrate that the Mean Absolute Percentage Error (MAPE) of this model for predicting total circuit power consumption is less than 1.71% when compared with the PTPX analysis results following physical design back-annotation. The model takes less than 1.2 s to predict the power curve for 11k clock cycles. In cross-validation experiments with different scenarios, the prediction error of the model is found to be less than 4.5%.
-
表 1 神经网络模型的测试用例
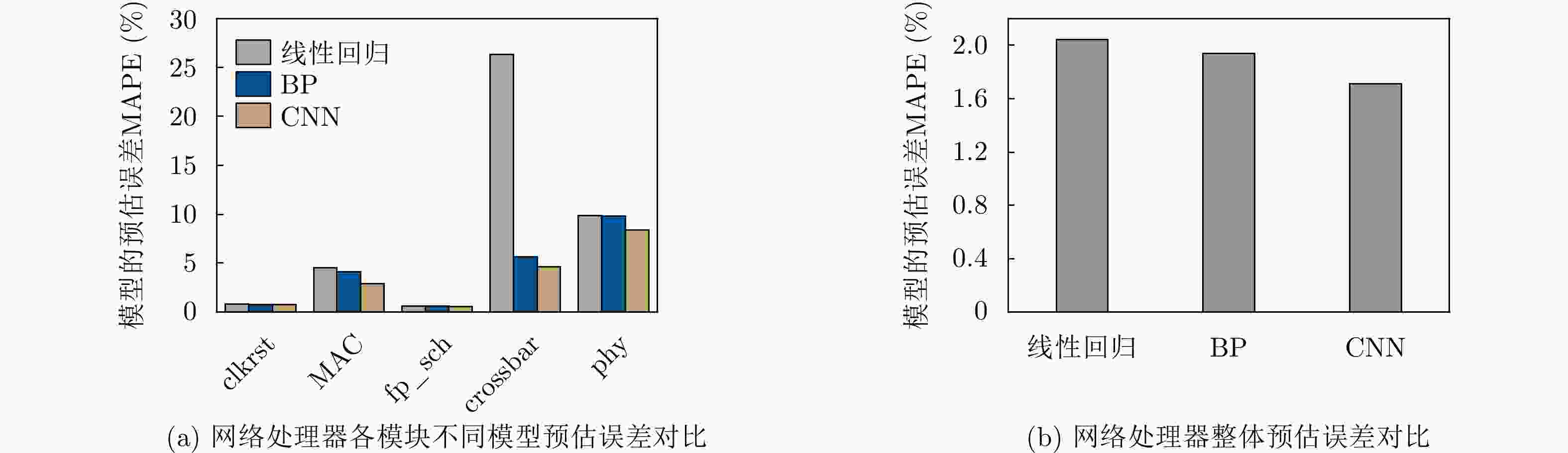
电路名称 电路描述 电路规模 仿真场景(样本数) float-adder 32位浮点加法器 约1500门 随机激励(220k) RISC-V Core 简易的RISC-V核心 约10000门 单一场景测试(850k) AES AES加密算法 约30000门 随机测试(84k) MAC 媒体访问控制层协议 约400000门 随机测试(95k) FIFO 8位宽16深度的同步FIFO 约1000门 随机测试(80k) light8080 简易的8080处理器 约10000门 随机测试(4 800k) 表 2 不同模型的预测误差(MAPE)(%)
电路名称 CNN LSTM 线性
回归BP ResNet18 CNN_PRIMAL float-adder 4.29 4.32 4.39 4.38 6.44 2.83 RISC-V Core 0.23 0.08 0.78 0.66 4.96 0.39 AES 0.19 0.56 0.34 0.81 1.75 1.85 MAC 1.15 0.34 3.44 1.89 4.63 – FIFO 4.78 4.77 4.80 4.85 5.06 – light8080 0.11 0.05 0.14 0.15 2.95 – 平均误差 1.79 1.69 2.31 2.12 4.30 – 表 3 不同模型训练耗时(s)
电路名称 CNN LSTM 线性回归 BP ResNet18 CNN_PRIMAL float-adder 1.47 8.25 1.64 1.45 10.34 23.41 RISC-V Core 1.03 63.55 0.80 2.52 43.39 19.52 AES 1.03 263.69 0.67 4.98 56.19 25.80 MAC 0.55 128.53 0.31 1.70 18.28 – FIFO 0.27 5.20 0.22 0.31 1.92 – light8080 1.69 31.64 1.30 1.70 24.67 – 总耗时 6.03 500.86 4.94 12.67 154.80 – 表 4 场景交叉验证结果
测试场景 样本数量 建模耗时(s) 预测耗时(s) 预测误差
MAPE(%)动作测试 约11k 451.35 1.20 4.41 单播流控分类 约5.6k 661.74 0.60 1.86 单播线速 约4k 698.76 0.43 1.79 单播学习 约3.4k 713.61 0.38 1.76 组播测试 约1.5k 776.25 0.19 2.82 -
[1] RAUT K J, CHITRE A V, DESHMUKH M S, et al. Low power VLSI design techniques: A review[J]. Journal of University of Shanghai for Science and Technology, 2021, 23(11): 172–183. doi: 10.51201/JUSST/21/11881 [2] REN Haoxing and HU Jiang. Machine Learning Applications in Electronic Design Automation[M]. Cham: Springer, 2023. [3] SROUR M. Data-dependent cycle-accurate power modeling of RTL-level IPs using machine learning[D]. [Master dissertation], The University of Texas at Austin, 2018. [4] DHOTRE H, EGGERSGLÜß S, CHAKRABARTY K, et al. Machine learning-based prediction of test power[C]. 2019 IEEE European Test Symposium (ETS), Baden-Baden, Germany, 2019: 1–6. [5] NASSER Y, SAU C, PRÉVOTET J C, et al. NeuPow: A CAD methodology for high-level power estimation based on machine learning[J]. ACM Transactions on Design Automation of Electronic Systems, 2020, 25(5): 41. doi: 10.1145/3388141 [6] ZHOU Yuan, REN Haoxing, ZHANG Yanqing, et al. PRIMAL: Power inference using machine learning[C]. The 56th Annual Design Automation Conference 2019, Las Vegas, USA, 2019: 39. [7] KIM D, ZHAO J, BACHRACH J, et al. Simmani: Runtime power modeling for arbitrary RTL with automatic signal selection[C]. The 52nd Annual IEEE/ACM International Symposium on Microarchitecture, Columbus, USA, 2019: 1050–1062. [8] XIE Zhiyao, XU Xiaoqing, WALKER M, et al. APOLLO: An automated power modeling framework for runtime power introspection in high-volume commercial microprocessors[C/OL]. MICRO-54: 54th Annual IEEE/ACM International Symposium on Microarchitecture, 2021: 1–14. [9] PUNDIR N, PARK J, FARAHMANDI F, et al. Power side-channel leakage assessment framework at register-transfer level[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2022, 30(9): 1207–1218. doi: 10.1109/TVLSI.2022.3175067 [10] HUANG Guyue, HU Jingbo, HE Yifan, et al. Machine learning for electronic design automation: A survey[J]. ACM Transactions on Design Automation of Electronic Systems, 2021, 26(5): 40. doi: 10.1145/3451179 [11] FAN Jianqing and LI Runze. Variable selection via nonconcave penalized likelihood and its oracle properties[J]. Journal of the American statistical Association, 2001, 96(456): 1348–1360. doi: 10.1198/016214501753382273 [12] TIAN Yingjie and ZHANG Yuqi. A comprehensive survey on regularization strategies in machine learning[J]. Information Fusion, 2022, 80: 146–166. doi: 10.1016/j.inffus.2021.11.005 [13] SCHÜRMANS S, ONNEBRINK G, LEUPERS R, et al. ESL power estimation using virtual platforms with black box processor models[C]. The 2015 International Conference on Embedded Computer Systems: Architectures, Modeling, and Simulation (SAMOS), Samos, Greece, 2015: 354–359. [14] ZHANG Xianda. Modern Signal Processing[M]. Tsinghua University Press, 2022: 497–564. [15] ZHOU Guochang, GUO Baolong, GAO Xiang, et al. A FPGA power estimation method based on an improved BP neural network[C]. 2015 International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP), Adelaide, Australia, 2015: 251–254, [16] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. The 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. [17] CHHABRIA V A, AHUJA V, PRABHU A, et al. Thermal and IR drop analysis using convolutional encoder-decoder networks[C]. The 26th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 2021: 690–696. [18] FARAWAY J J. Linear Models with R[M]. 2nd ed. New York: CRC Press, 2014. [19] JEON H and OH S. Hybrid-recursive feature elimination for efficient feature selection[J]. Applied Sciences, 2020, 10(9): 3211. doi: 10.3390/app10093211 [20] XUAN Yi, SI Weiguo, ZHU Zhu, et al. Multi-model fusion short-term load forecasting based on random forest feature selection and hybrid neural network[J]. IEEE Access, 2021, 9: 69002–69009. doi: 10.1109/ACCESS.2021.3051337 -





 下载:
下载:


 下载:
下载:
