Interference Image Registration Based on FPDE-SIFT for Sonar
-
摘要: 图像配准是声呐进行高精度干涉测量的保障,该文针对水下目标的声呐图像配准,提出了一种基于4阶偏微分方程尺度不变特征变换的声呐干涉图像配准方法。该方法聚焦声呐图像配准的难点,首先基于4阶偏微分方程构建尺度空间,在保持图像细节的前提下滤除噪声,提高特征提取的准确度;对于残余噪声造成的特征点误检,借助特征点的相位一致性信息加以筛选,精简特征点样本集;最后对特征点匹配策略进行优化,提出改进的快速样本一致性匹配策略剔除特征点的误匹配。算法增加了匹配点对的数量,提高了匹配点对的准确度,实现了声呐干涉图像的精确配准。水池实验和外场试验表明,该文所提出的算法相较现有算法对声呐图像有着更好的适用性,配准后的均方根误差与留一法均方根均小于1像素,达到了亚像素配准精度。Abstract: Image registration is the cornerstone of sonar for high-precision interferometry. This study presents an innovative method for registering sonar interference images, utilizing the Fourth-order Partial Differential Equation (FPDE) in conjunction with the scale-invariant feature transform. This technique is specifically tailored for underwater sonar targets. This method specifically addresses the challenges associated with sonar image registration. First, we establish the scale space by employing the FPDE. This process filters noise while preserving image details, resulting in an improved accuracy of feature extraction. The proposed method utilizes phase congruency information to counter false feature point detection due to the residual noise, thereby screening and simplifying the sample set of feature points. Ultimately, the features point matching strategy undergoes optimization, with an enhanced fast sample consensus matching strategy proposed to rectify feature point mismatches. The algorithm increases the number of matching point pairs and augments their precision, ultimately achieving precise registration of sonar interference images. Rigorous tests, both under controlled conditions and lake environments, demonstrate the algorithm’s superior applicability to sonar images compared with existing approaches. The root-mean-square-error and mean-square-error are calculated post-registration using leave-one-out analysis, both are under one pixel, attesting to the algorithm’s achievement of sub-pixel registration accuracy.
-
表 1 水池实验算法性能量化对比
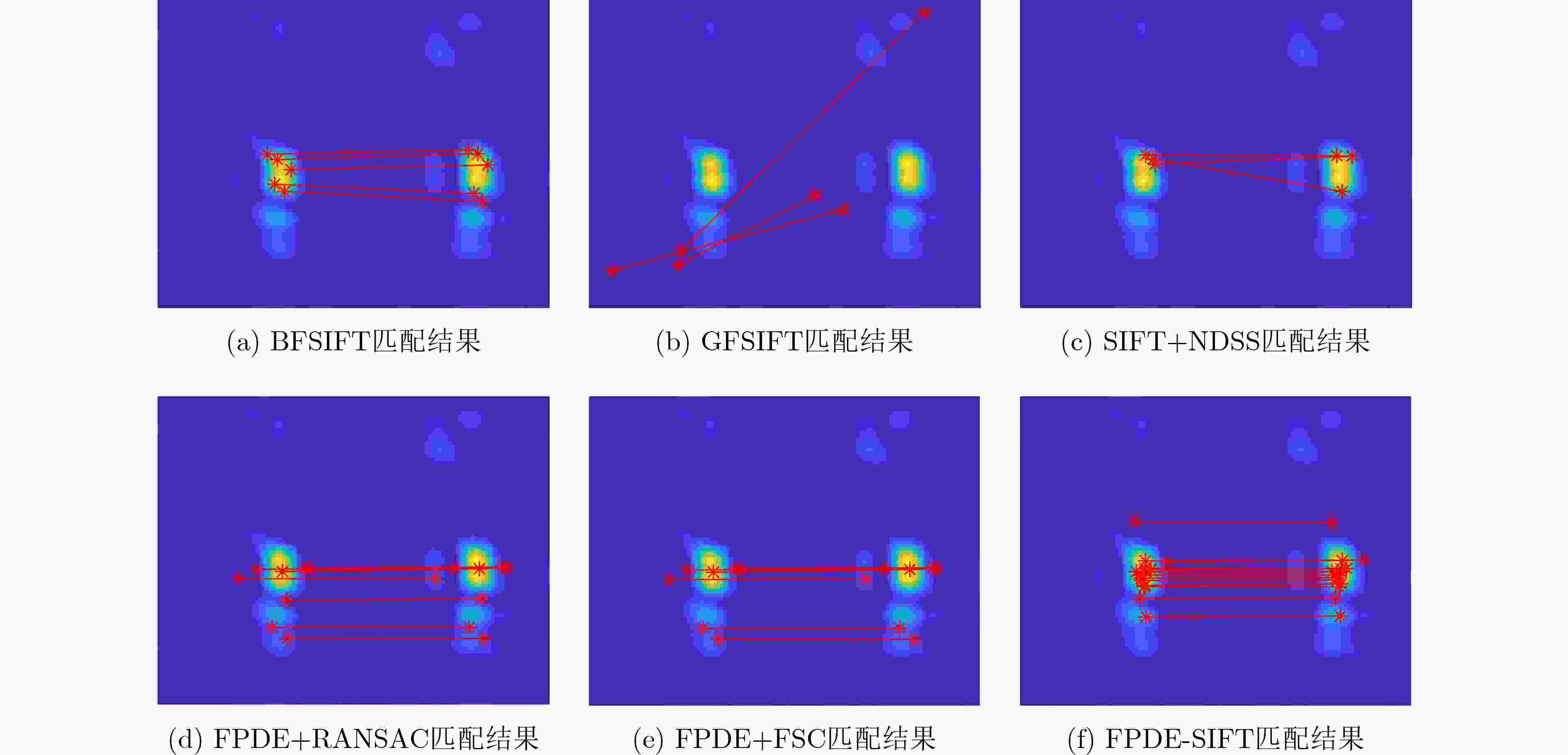
水池实验 特征点 RMSE(像素) $ {\text{RMS}}_{\text{LOO}} $(像素) 时间(s) 参考图像 配准图像 匹配点数 BFSIFT 35 60 5 0.4465 1.1818 8.979 GFSIFT 31 31 3 / / 6.275 SIFT+NDSS 8 17 3 / / 7.1 FPDE+RANSAC 97 73 8 0.8687 1.3220 8.012 FPDE+FSC 97 73 7 0.7313 1.2478 7.978 FPDE-SIFT 97 73 14 0.4139 0.6292 7.372 表 2 外场试验算法性能量化对比
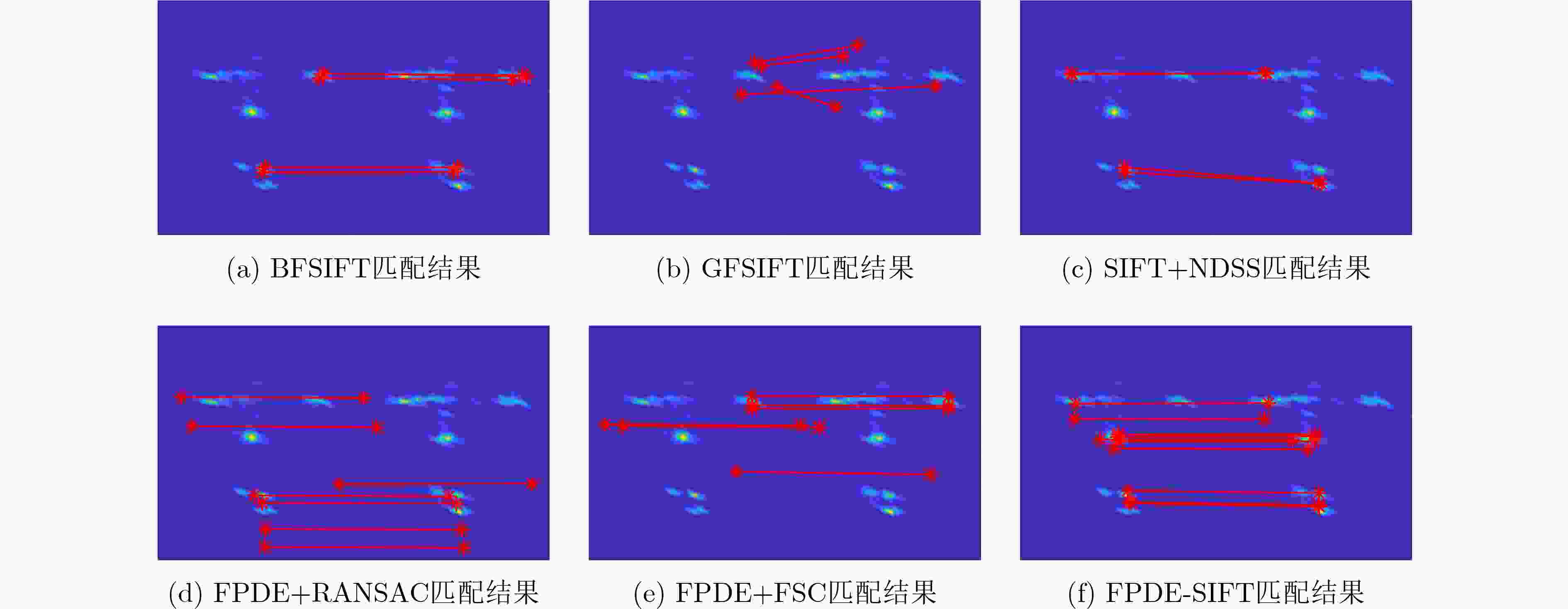
外场试验 特征点 RMSE(像素) RMSLOO(像素) 时间(s) 参考图像 配准图像 匹配点数 BFSIFT 119 145 5 0.5044 1.8628 9.488 GFSIFT 62 50 4 0.2934 3.8227 5.498 SIFT+NDSS 18 19 4 0.3344 2.2831 6.683 FPDE+RANSAC 191 215 7 0.4907 1.2073 7.944 FPDE+FSC 191 215 6 0.3357 0.7378 7.443 FPDE-SIFT 191 215 10 0.2820 0.5512 7.167 表 3 不同探测角度算法性能量化对比
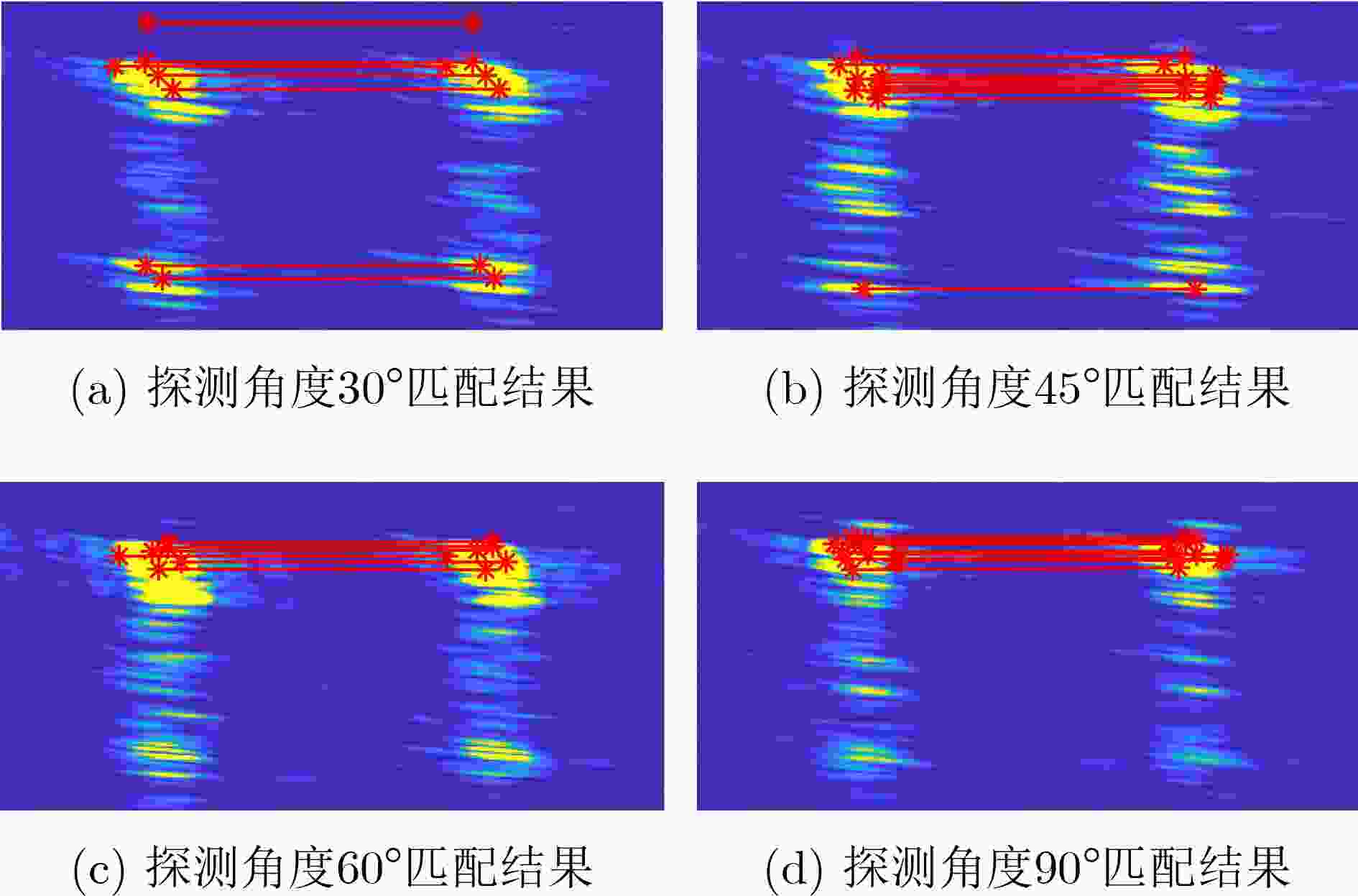
探测角度(°) 特征点 RMSE
(像素)RMSLOO
(像素)参考图像 配准图像 匹配点数 30 129 95 7 0.4414 0.7393 45 110 161 10 0.3523 0.7326 60 104 62 6 0.4308 0.7872 90 162 152 11 0.4922 0.8178 -
[1] SINTES C, LLORT-PUJOL G, and GUERIOT D. Coherent probabilistic error model for interferometric Sidescan sonars[J]. IEEE Journal of Oceanic Engineering, 2010, 35(2): 412–423. doi: 10.1109/JOE.2010.2043574 [2] SAEBØ T O, SYNNES S A V, and HANSEN R E. Wideband interferometry in synthetic aperture sonar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(8): 4450–4459. doi: 10.1109/TGRS.2013.2244900 [3] 徐超, 李海森, 陈宝伟, 等. 多波束相干海底成像技术[J]. 哈尔滨工程大学学报, 2013, 34(9): 1159–1164. doi: 10.3969/j.issn.1006-7043.201302007CHAO Xu, LI Haisen, CHEN Baowei, et al. Multibeam interferometric seafloor imaging technology[J]. Journal of Harbin Engineering University, 2013, 34(9): 1159–1164. doi: 10.3969/j.issn.1006-7043.201302007 [4] 周天, 沈嘉俊, 杜伟东, 等. 基于Khatri-Rao积的三维前视声呐空间方位估计技术[J]. 电子与信息学报, 2021, 43(3): 857–864. doi: 10.11999/JEIT200657ZHOU Tian, SHEN Jiajun, DU Weidong, et al. DOA estimation technology based on Khatri-Rao product for 3D forward-looking sonar[J]. Journal of Electronics &Information Technology, 2021, 43(3): 857–864. doi: 10.11999/JEIT200657 [5] 周天, 沈嘉俊, 陈宝伟, 等. 应用二维稀疏阵列的三维前视声呐方位估计[J]. 哈尔滨工程大学学报, 2020, 41(10): 1450–1456. doi: 10.11990/jheu.202007031ZHOU Tian, SHEN Jiajun, CHEN Baowei, et al. Direction-of-arrival estimation of three-dimensional forward-looking sonar with two-dimensional sparse array[J]. Journal of Harbin Engineering University, 2020, 41(10): 1450–1456. doi: 10.11990/jheu.202007031 [6] 黄攀, 唐劲松, 钟何平, 等. 基于有理函数曲面拟合的InSAS复图像配准新方法[J]. 武汉大学学报·信息科学版, 2019, 44(4): 601–607. doi: 10.13203/j.whugis20170167HUANG Pan, TANG Jinsong, ZHONG Heping, et al. A new InSAS registration method based on rational function surface fitting[J]. Geomatics and Information Science of Wuhan University, 2019, 44(4): 601–607. doi: 10.13203/j.whugis20170167 [7] 黄攀, 唐劲松, 钟何平. 干涉合成孔径声呐复图像配准分段曲面拟合法[J]. 武汉大学学报·信息科学版, 2021, 46(8): 1259–1264. doi: 10.13203/j.whugis20190306HUANG Pan, TANG Jinsong, and ZHONG Heping. Piecewise surface fitting method for complex image registration of interferometric synthetic aperture sonar[J]. Geomatics and Information Science of Wuhan University, 2021, 46(8): 1259–1264. doi: 10.13203/j.whugis20190306 [8] WANG V T and HAYES M P. Synthetic aperture sonar track registration using SIFT image correspondences[J]. IEEE Journal of Oceanic Engineering, 2017, 42(4): 901–913. doi: 10.1109/JOE.2016.2634078 [9] LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. doi: 10.1023/B:VISI.0000029664.99615.94 [10] 王山虎, 尤红建, 付琨. 基于大尺度双边SIFT的SAR图像同名点自动提取方法[J]. 电子与信息学报, 2012, 34(2): 287–293. doi: 10.3724/SP.J.1146.2011.00568WANG Shanhu, YOU Hongjian, and FU Kun. An automatic method for finding matches in SAR images based on coarser scale bilateral filtering SIFT[J]. Journal of Electronics &Information Technology, 2012, 34(2): 287–293. doi: 10.3724/SP.J.1146.2011.00568 [11] WANG Shanhu, YOU Hongjian, and FU Kun. BFSIFT: A novel method to find feature matches for SAR image registration[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 649–653. doi: 10.1109/LGRS.2011.2177437 [12] YU Qiuze, ZHOU Shan, JIANG Yuxuan, et al. High-performance SAR image matching using improved SIFT framework based on rolling guidance filter and ROEWA-powered feature[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(3): 920–933. doi: 10.1109/JSTARS.2019.2897171 [13] FAN Jianwei, WU Yan, WANG Fan, et al. SAR image registration using phase congruency and nonlinear diffusion-based SIFT[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(3): 562–566. doi: 10.1109/LGRS.2014.2351396 [14] WU Yue, MA Wenping, GONG Maoguo, et al. A novel point-matching algorithm based on fast sample consensus for image registration[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 43–47. doi: 10.1109/LGRS.2014.2325970 [15] CHUM O and MATAS J. Matching with PROSAC-progressive sample consensus[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, USA, 2005: 220–226. [16] RAGURAM R, CHUM O, POLLEFEYS M, et al. USAC: A universal framework for random sample consensus[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 2022–2038. doi: 10.1109/TPAMI.2012.257 [17] 金广. 基于特征点的侧扫声呐图像拼接技术研究[D]. [硕士论文], 哈尔滨工程大学, 2015.JIN Guang. Research on side-scan sonar image mosaic based on feature point[D]. [Master dissertation], Harbin Engineering University, 2015. [18] 黄鹏. 基于深度学习的前视声呐图像配准研究[D]. [硕士论文], 杭州电子科技大学, 2022.HUANG Peng. Research on forward-looking sonar image registration based on deep learning[D]. [Master dissertation], Hangzhou Dianzi University, 2022. [19] BAVIRISETTI D P, XIAO Gang, and LIU Gang. Multi-sensor image fusion based on fourth order partial differential equations[C]. The 20th International Conference on Information Fusion (Fusion), Xian, China, 2017, 701–709. [20] YOU Y L and MOSTAFA K. Fourth-order partial differential equations for noise removal[J]. IEEE Transactions on Image Processing, 2000, 9(10): 1723–1730. doi: 10.1109/83.869184 [21] WONG A and CLAUSI D A. ARRSI: Automatic registration of remote-sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5): 1483–1493. doi: 10.1109/TGRS.2007.892601 [22] 王延钊, 苏娟. 基于相干斑抑制SIFT的SAR图像配准方法[J]. 系统工程与电子技术, 2017, 39(12): 2697–2703. doi: 10.3969/j.issn.1001-506X.2017.12.10WANG Yanzhao and SU Juan. SAR image registration algorithm based on speckle reducing SIFT[J]. Systems Engineering and Electronics, 2017, 39(12): 2697–2703. doi: 10.3969/j.issn.1001-506X.2017.12.10 [23] GONCALVES H, GONCALVES J A, and CORTE-REAL L. Measures for an objective evaluation of the geometric correction process quality[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(2): 292–296. doi: 10.1109/LGRS.2008.2012441 -





 下载:
下载:



 下载:
下载:
