一种基于完全互补码波形设计的抗间歇式采样转发干扰方法

余涛; 周正春; 杜小勇; 鲍庆龙; 何元

doi:10.11999/JEIT230331

一种基于完全互补码波形设计的抗间歇式采样转发干扰方法

doi: 10.11999/JEIT230331

余涛¹,
周正春^2, ,,
杜小勇³,
鲍庆龙³,
何元⁴

1.
西南交通大学数学学院成都 610031
2.
西南交通大学信息科学与技术学院成都 610031
3.
国防科技大学电子科学学院长沙 410073
4.
北京邮电大学信息与通信工程学院北京 100876

基金项目: 国家自然科学基金(62131016, 62071397)

详细信息

作者简介:
余涛：男，博士生，研究方向为雷达波形设计、雷达抗干扰技术

周正春：男，教授，研究方向为编码理论、通信/雷达波形设计、电子信息对抗

杜小勇：男，研究员，研究方向为雷达成像、雷达信号处理与目标识别

鲍庆龙：男，研究员，研究方向为雷达系统设计、雷达信号处理

何元：男，研究员，研究方向为雷达与电子侦察对抗

通讯作者:
周正春　zzc@swjtu.edu.cn

中图分类号: TN974
计量
- 文章访问数: 621
- HTML全文浏览量: 320
- PDF下载量: 113
- 被引次数: 0
出版历程
- 收稿日期: 2023-04-26
- 修回日期: 2023-07-07
- 网络出版日期: 2023-07-13
- 刊出日期: 2023-11-28

An Anti-Interrupted Sampling Repeater Jamming Method Based on Complete Complementary Code Waveform Design

1.
School of Mathematics, Southwest Jiaotong University, Chengdu 610031, China
2.
School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, China
3.
The College of Electronic Science and Technology, National University of Defense Technology, Changsha 410073, China
4.
School of Communication and Information Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China

Funds: The National Natural Science Foundation of China (62131016, 62071397)

摘要

摘要: 间歇采样转发干扰(ISRJ)是一种先进的有源相干干扰技术，对雷达的探测性能有较大的影响，且现有抗ISRJ的方法需要求解复杂的波形优化问题以及需进行干扰识别和剔除。于是，在深入研究ISRJ的基础上，该文基于完全互补码提出一种抗ISRJ的方法。针对ISRJ时域采样不连续的特点，该文首先通过脉内频域正交的方法将完全互补码中的所有互补波形按照子脉冲掩护的方式编入单个脉冲雷达波形。然后，基于脉内分段脉冲压缩的处理方式，利用完全互补码波形的理想互相关和自相关特性，设计非匹配滤波器系数在抑制ISRJ的同时能得到较低的距离旁瓣。相比于现有抗ISRJ的方法，所提方法在线设计能力更强且无需进行干扰识别和剔除。仿真实验表明所设计波形能有效对抗多种样式的ISRJ且具有较高的多普勒容忍度。
- 间歇采样转发干扰 /
- 完全互补码波形 /
- 非匹配滤波 /
- 波形设计 /
- 多普勒容忍
Abstract: Interrupted Sampling Repeater Jamming (ISRJ) is an advanced active coherent jamming technology, which has great influence on the detection performance of radar, and the existing anti-ISRJ methods need to solve complex waveform optimization problems and interference recognition and elimination. Therefore, on the basis of in-depth study of ISRJ, an anti-ISRJ method based on complete complementary codes is proposed. Considering the characteristics of ISRJ sampling discontinuity in time domain, all complementary waveforms in the complete complementary code are integrated into a single pulse radar waveform through sub-pulse cover using the method of orthogonal in the frequency domain. Then, based on the intra-pulse segmental pulse compression processing method, utilizing the ideal cross-correlation and autocorrelation characteristics of the complete complementary code waveform, the mismatched filter coefficients are designed to suppress ISRJ and obtain lower range sidelobes. Compared to existing anti-ISRJ methods, the proposed method has stronger online design capability and obviates the need for interference recognition and elimination. The simulation results demonstrate that the various ISRJs can be effectively suppressed by the designed waveform and has high Doppler tolerance.
- Interrupted Sampling Repeater Jamming(ISRJ) /
- Complete complementary code /
- Mismatched filter /
- Waveform design /
- Doppler tolerance

HTML全文

图 1 完全互补码的相关函数

下载: 全尺寸图片幻灯片

图 2 间歇采样转发干扰示意图

下载: 全尺寸图片幻灯片

图 3 单脉冲互补波形时频域示意图

下载: 全尺寸图片幻灯片

图 4 分段脉压处理示意图

下载: 全尺寸图片幻灯片

图 5 同步采样直接转发干扰回波处理结果

下载: 全尺寸图片幻灯片

图 6 同步采样重复转发干扰回波处理结果

下载: 全尺寸图片幻灯片

图 7 不同干扰参数下ISRJ信号脉压输出峰值

下载: 全尺寸图片幻灯片

图 8 完全互补码的性能分析

下载: 全尺寸图片幻灯片

图 9 运动目标脉压处理结果

下载: 全尺寸图片幻灯片

图 10 本文完全互补码波形的模糊函数

下载: 全尺寸图片幻灯片

表 1 直接转发干扰仿真参数

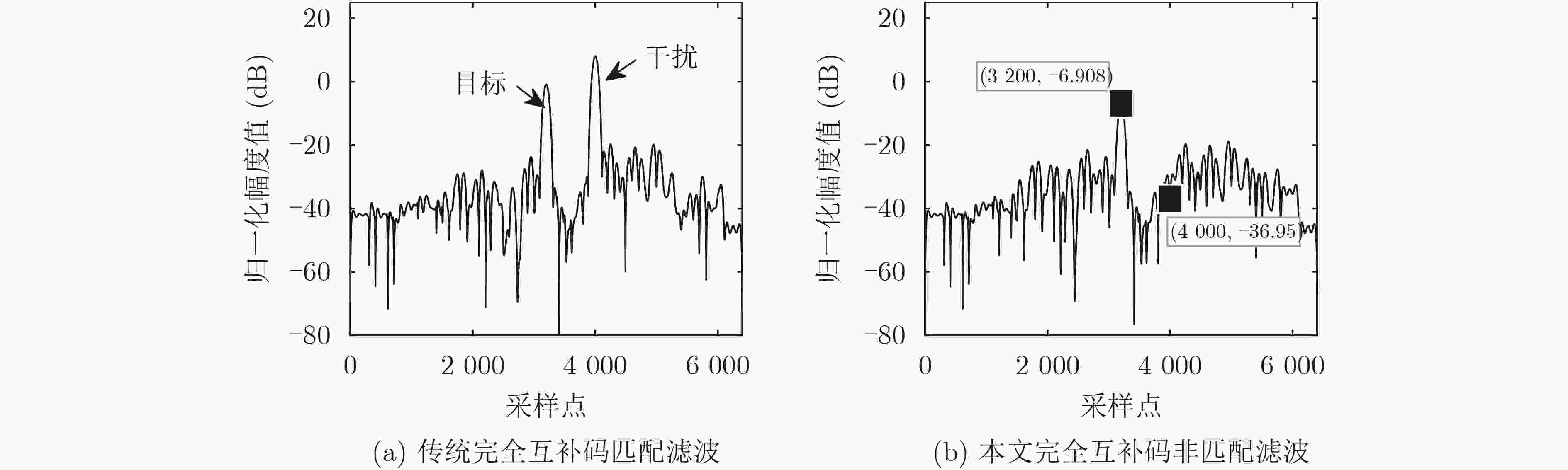
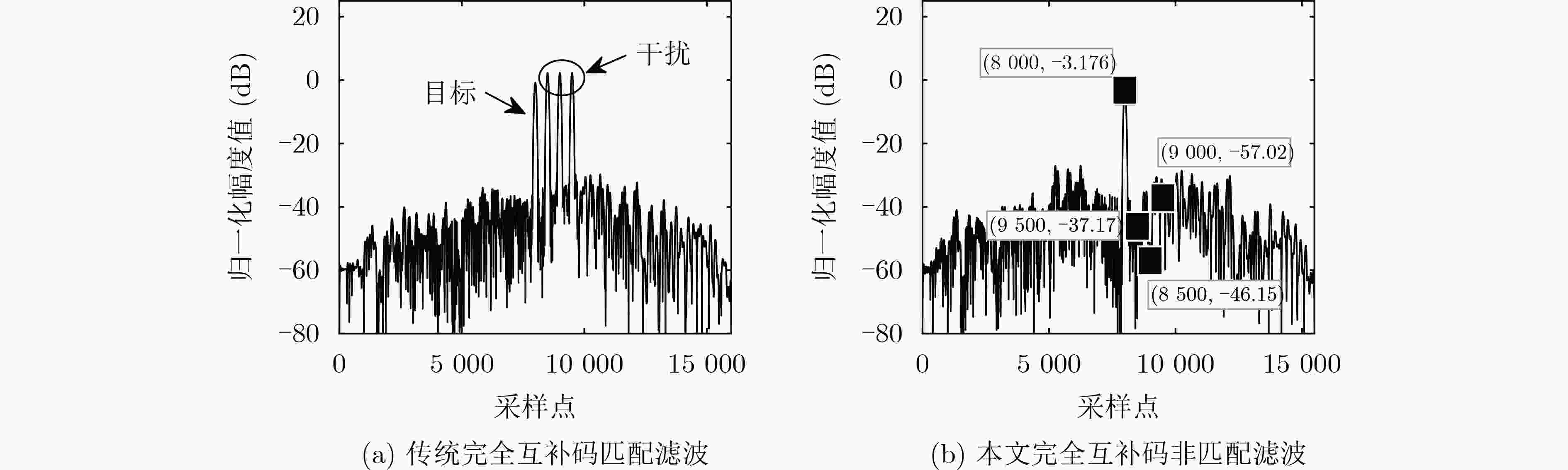
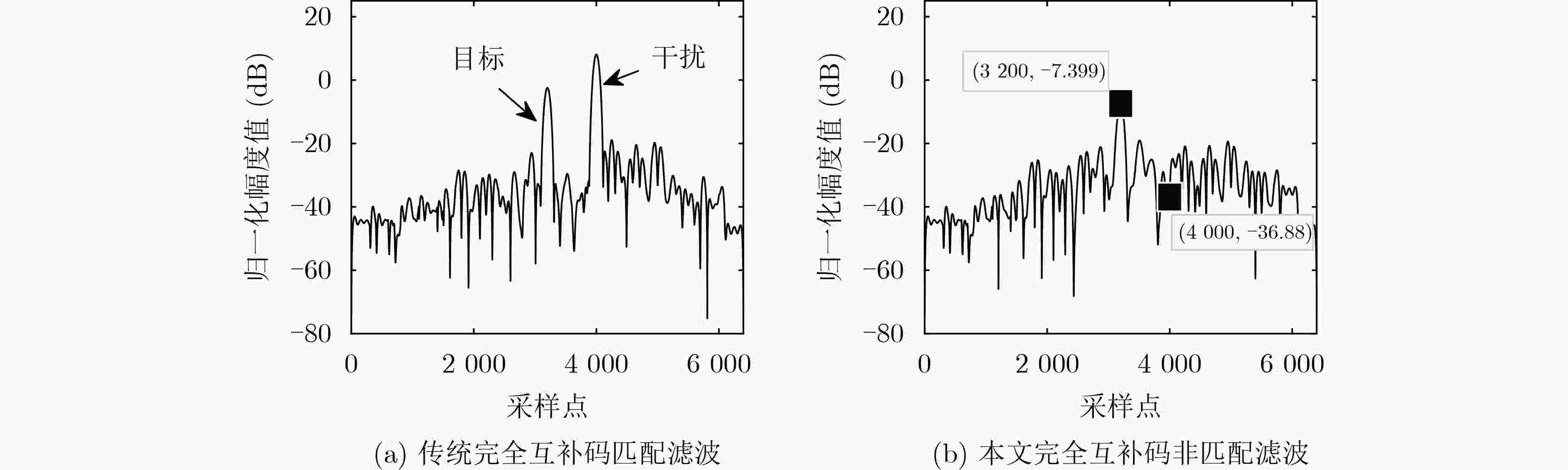
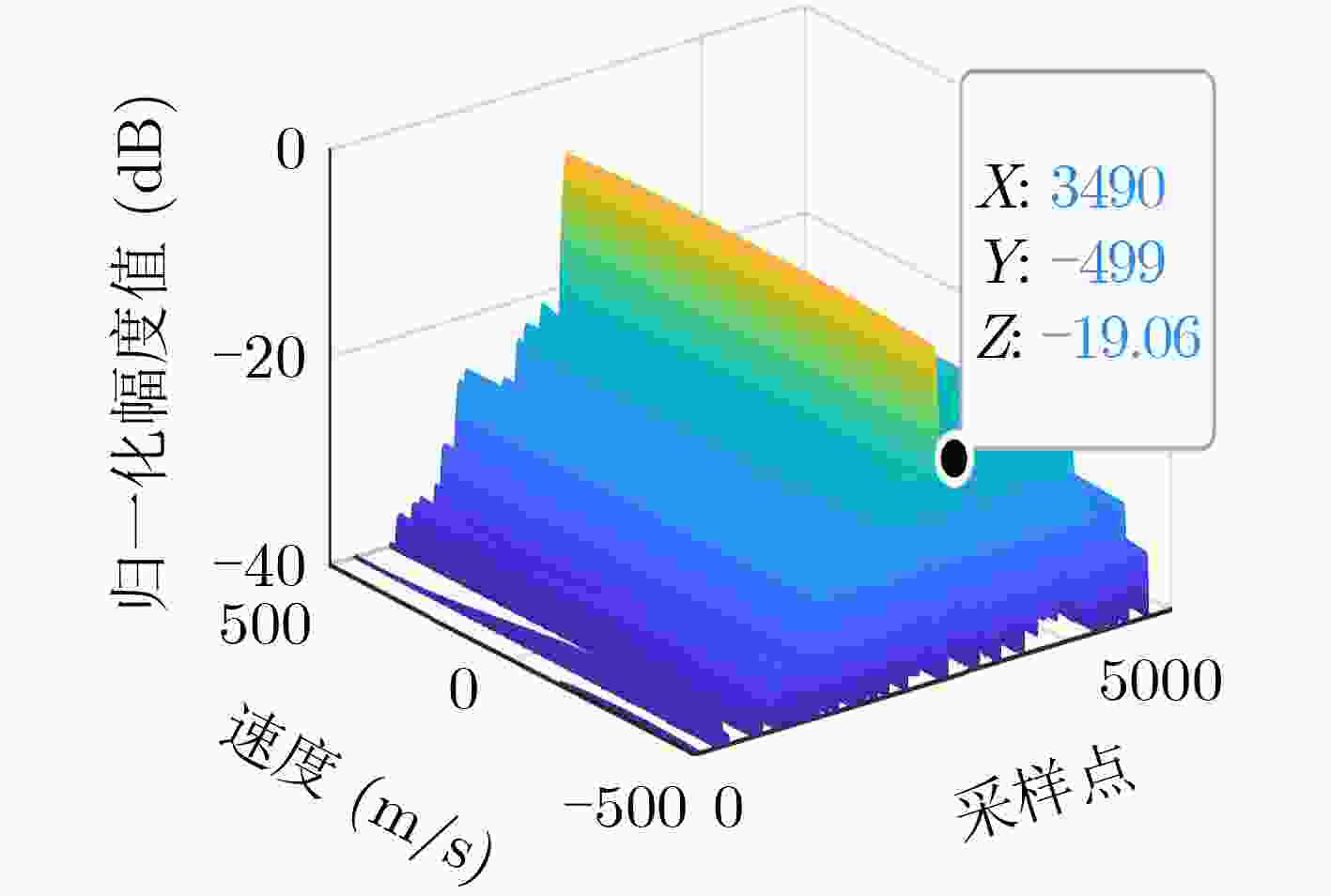
参数	数值
完全互补码维度	(2,2,8)
完全互补码	$ {x_{0,0}} = \left[ {{{1,1,1, - 1,1,1, - 1,1}}} \right] $, $ {x_{0,1}} = \left[ {{{1, - 1,1,1,1, - 1, - 1, - 1}}} \right] $, $ {x_{1,0}} = \left[ {{{ - 1, - 1, - 1,1,1,1, - 1,1}}} \right] $, ${x_{1,1} }=\left[ { { { - 1,1, - 1, - 1,1, - 1, - 1, - 1} } } \right]$
中心频率(MHz)	1, 3, 5, 7
滤波器带宽(MHz)	2
码元宽度(µs)	1
采样率(MHz)	100
脉宽(µs)	32
目标所处采样点位置	3 200
ISRJ干扰机所处采样点位置	4 000
直接转发干扰采样脉宽(µs)	8
直接转发干扰采样重复周期(µs)	16
信干比(dB)	–15
信噪比(dB)	0

下载: 导出CSV

参考文献(25)

[1]	FENG Dejun, XU Letao, PAN Xiaoyi, et al. Jamming wideband radar using interrupted-sampling repeater[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1341–1354. doi: 10.1109/TAES.2017.2670958
[2]	李永祯, 黄大通, 邢世其, 等. 合成孔径雷达干扰技术研究综述[J]. 雷达学报, 2020, 9(5): 753–764. doi: 10.12000/JR20087 LI Yongzhen, HUANG Datong, XING Shiqi, et al. A review of synthetic aperture radar jamming technique[J]. Journal of Radars, 2020, 9(5): 753–764. doi: 10.12000/JR20087
[3]	SOUMEKH M. SAR-ECCM using phase-perturbed LFM chirp signals and DRFM repeat jammer penalization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 191–205. doi: 10.1109/TAES.2006.1603414
[4]	王雪松, 刘建成, 张文明, 等. 间歇采样转发干扰的数学原理[J]. 中国科学E辑:信息科学, 2007, 50(1): 113–123. doi: 10.3969/J.issn.1674-7259.2006.08.007 WANG Xuesong, LIU Jiancheng, ZHANG Wenming, et al. Mathematic principles of interrupted-sampling repeater jamming (ISRJ)[J]. Science in China Series F:Information Sciences, 2007, 50(1): 113–123. doi: 10.3969/J.issn.1674-7259.2006.08.007
[5]	刘忠, 王雪松, 刘建成, 等. 基于数字射频存储器的间歇采样重复转发干扰[J]. 兵工学报, 2008, 29(4): 405–410. doi: 10.3321/j.issn:1000-1093.2008.04.005 LIU Zhong, WANG Xuesong, LIU Jiancheng, et al. Jamming technique of interrupted-sampling and periodic repeater based on digital radio frequency memory[J]. Acta Armamentarii, 2008, 29(4): 405–410. doi: 10.3321/j.issn:1000-1093.2008.04.005
[6]	周超, 刘泉华, 胡程. 间歇采样转发式干扰的时频域辨识与抑制[J]. 雷达学报, 2019, 8(1): 100–106. doi: 10.12000/JR18080 ZHOU Chao, LIU Quanhua, and HU Cheng. Time-frequency analysis techniques for recognition and suppression of interrupted sampling repeater jamming[J]. Journal of Radars, 2019, 8(1): 100–106. doi: 10.12000/JR18080
[7]	杨少奇, 田波, 周瑞钊. 利用时频分析的间歇采样干扰对抗方法[J]. 信号处理, 2016, 32(10): 1244–1251. doi: 10.16798/j.issn.1003-0530.2016.10.14 YANG Shaoqi, TIAN Bo, and ZHOU Ruizhao. ECCM against interrupted sampling repeater jamming based on time-frequency analysis[J]. Journal of Signal Processing, 2016, 32(10): 1244–1251. doi: 10.16798/j.issn.1003-0530.2016.10.14
[8]	刘智星, 杜思予, 吴耀君, 等. 脉间-脉内捷变频雷达抗间歇采样干扰方法[J]. 雷达学报, 2022, 11(2): 301–312. doi: 10.12000/JR22001 LIU Zhixing, DU Siyu, WU Yaojun, et al. Anti-interrupted sampling repeater jamming method for interpulse and intrapulse frequency-agile radar[J]. Journal of Radars, 2022, 11(2): 301–312. doi: 10.12000/JR22001
[9]	盖季妤, 姜维, 张凯翔, 等. 基于差分特征的间歇采样转发干扰辨识与抑制方法[J]. 雷达学报, 2023, 12(1): 186–196. doi: 10.12000/JR22058 GAI Jiyu, JIANG Wei, ZHANG Kaixiang, et al. A method for interrupted-sampling repeater jamming identification and suppression based on differential features[J]. Journal of Radars, 2023, 12(1): 186–196. doi: 10.12000/JR22058
[10]	周畅, 汤子跃, 余方利, 等. 基于脉内正交的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506x.2017.02.06 ZHOU Chang, TANG Ziyue, YU Fangli, et al. Anti intermittent sampling repeater jamming method based on intrapulse orthogonality[J]. Systems Engineering and Electronics, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506x.2017.02.06
[11]	周畅, 汤子跃, 朱振波, 等. 抗间歇采样转发干扰的波形设计方法[J]. 电子与信息学报, 2018, 40(9): 2198–2205. doi: 10.11999/JEIT171236 ZHOU Chang, TANG Ziyue, ZHU Zhenbo, et al. Anti-interrupted sampling repeater jamming waveform design method[J]. Journal of Electronics &Information Technology, 2018, 40(9): 2198–2205. doi: 10.11999/JEIT171236
[12]	何金阳, 程子扬, 李绽蕾, 等. 低多普勒敏感的抗间歇采样转发干扰波形设计方法[J]. 系统工程与电子技术, 2023, 45(5): 1333–1341. doi: 10.12305/j.issn.1001-506X.2023.05.09 HE Jinyang, CHEN Ziyang, LI Zhanlei, et al. Low Doppler sensitive waveform design method against interrupted sampling repeater jamming[J]. Systems Engineering and Electronics, 2023, 45(5): 1333–1341. doi: 10.12305/j.issn.1001-506X.2023.05.09
[13]	张建中, 穆贺强, 文树梁, 等. 基于LFM分段脉冲压缩的抗间歇采样转发干扰方法[J]. 电子与信息学报, 2019, 41(7): 1712–1720. doi: 10.11999/JEIT180851 ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti-intermittent sampling repeater jamming method based on LFM segmented pulse compression[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1712–1720. doi: 10.11999/JEIT180851
[14]	张建中, 穆贺强, 文树梁, 等. 基于脉内步进LFM波形的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12 ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti interrupted-sampling repeater jamming method based on stepped LFM waveform[J]. Systems Engineering and Electronics, 2019, 41(5): 1013–1020. doi: 10.3969/j.issn.1001-506X.2019.05.12
[15]	张建中, 穆贺强, 文树梁, 等. 基于脉内LFM-Costas频率步进的抗间歇采样干扰方法[J]. 系统工程与电子技术, 2019, 41(10): 2170–2177. doi: 10.3969/j.issn.1001-506X.2019.10.03 ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti-intermittent sampling jamming method based on intra-pulse LFM-Costas frequency stepping[J]. Systems Engineering and Electronics, 2019, 41(10): 2170–2177. doi: 10.3969/j.issn.1001-506X.2019.10.03
[16]	ZHOU Kai, LI Dexin, SU Yi, et al. Joint design of transmit waveform and mismatch filter in the presence of interrupted sampling repeater jamming[J]. IEEE Signal Processing Letters, 2020, 27: 1610–1614. doi: 10.1109/LSP.2020.3021667
[17]	ZHOU Kai, LI Dexin, QUAN Sinong, et al. SAR waveform and mismatched filter design for countering interrupted-sampling repeater jamming[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5214514. doi: 10.1109/TGRS.2021.3107328
[18]	王福来, 庞晨, 殷加鹏, 等. 一种多普勒容忍的抗间歇采样转发干扰恒模互补波形和接收滤波器联合设计方法[J]. 雷达学报, 2022, 11(2): 278–288. doi: 10.12000/JR22020 WANG Fulai, PANG Chen, YIN Jiapeng, et al. Joint design of Doppler-tolerant complementary sequences and receiving filters against interrupted sampling repeater jamming[J]. Journal of Radars, 2022, 11(2): 278–288. doi: 10.12000/JR22020
[19]	唐泽家, 鲍庆龙, 戴华骅, 等. 单脉冲脉内互补低距离旁瓣雷达波形设计[J]. 信号处理, 2022, 38(10): 2030–2040. doi: 10.16798/j.issn.1003-0530.2022.10.004 TANG Zejia, BAO Qinglong, DAI Huahua, et al. Intra-pulse complementary radar waveform design with low pulse compression sidelobe level[J]. Journal of Signal Processing, 2022, 38(10): 2030–2040. doi: 10.16798/j.issn.1003-0530.2022.10.004
[20]	SUEHIRO N and HATORI M. N-shift cross-orthogonal sequences[J]. IEEE Transactions on Information Theory, 1988, 34(1): 143–146. doi: 10.1109/18.2615
[21]	张妤歆, 洪升, 付勇强, 等. 基于完全互补码波形的非零多普勒目标检测[J]. 雷达科学与技术, 2022, 20(4): 442–448. doi: 10.3969/j.issn.1672-2337.2022.04.013 ZHANG Yuxin, HONG Sheng, FU Yongqiang, et al. Nonzero doppler target detection based on CCC waveform[J]. Radar Science and Technology, 2022, 20(4): 442–448. doi: 10.3969/j.issn.1672-2337.2022.04.013
[22]	TSENG C C and LIU C L. Complementary sets of sequences[J]. IEEE Transactions on Information Theory, 1972, 18(5): 644–652. doi: 10.1109/TIT.1972.1054860
[23]	GU Zhi, ZHOU Zhengchun, ADHIKARY A R, et al. Asymptotically optimal Golay-ZCZ sequence sets with flexible length[J]. Chinese Journal of Electronics, 2023, 32(4): 806–820. doi: 10.23919/cje.2022.00.266
[24]	YU Tao, ADHIKARY A R, WANG Yanyan, et al. New class of optimal Z-complementary code sets[J]. IEEE Signal Processing Letters, 2022, 29: 1477–1481. doi: 10.1109/LSP.2022.3185893
[25]	SARKAR P, LIU Zilong, and MAJHI S. Multivariable function for new complete complementary codes with arbitrary lengths[EB/OL].https://arxiv.org/abs/2102.10517, 2021.