NN-EdgeBuilder: High-performance Neural Network Inference Framework for Edge Devices
-
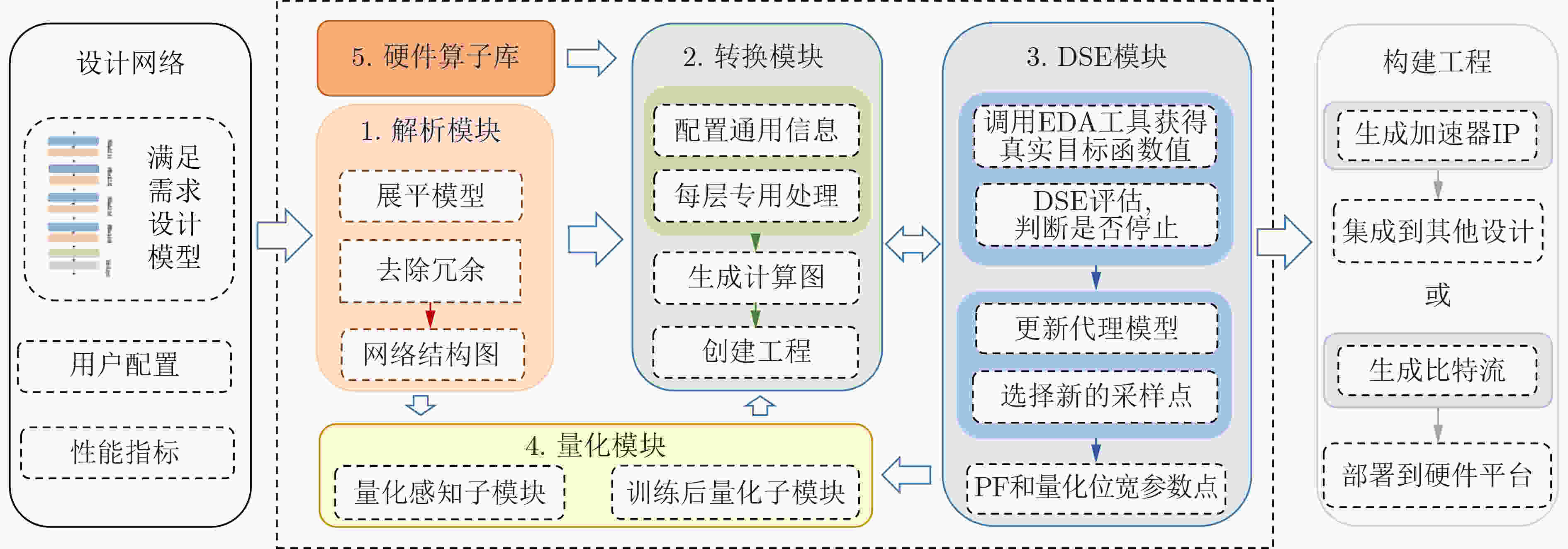
摘要: 飞速发展的神经网络已经在目标检测等领域取得了巨大的成功,通过神经网络推理框架将网络模型高效地自动部署在各类边缘端设备上是目前重要的研究方向。针对以上问题,该文设计一个针对边缘端FPGA的神经网络推理框架NN-EdgeBuilder,能够利用基于多目标贝叶斯优化的设计空间探索算法充分探索网络每层的并行度因子和量化位宽,接着调用高性能且通用的硬件加速算子来生成低延迟、低功耗的神经网络加速器。该文使用NN-EdgeBuilder在Ultra96-V2 FPGA上部署了UltraNet和VGG网络,生成的UltraNet-P1加速器与最先进的UltraNet定制加速器相比,功耗和能效比表现分别提升了17.71%和21.54%。与主流的推理框架相比,NN-EdgeBuilder生成的VGG加速器能效比提升了4.40倍,数字信号处理器(DSP)的计算效率提升了50.65%。Abstract: The rapidly developing neural network has achieved great success in fields such as target detection. Currently, an important research direction is to deploy efficiently and automatically network models on various edge devices through a neural network inference framework. In response to these issues, a neural network inference framework NN-EdgeBuilder for edge FPGA is designed in this paper, which can fully explore the parallelism factors and quantization bit widths of each layer of the network through a design space exploration algorithm based on multi-objective Bayesian optimization. Then high-performance and universal hardware acceleration operators are called to generate low-latency and low-power neural network accelerators. NN-EdgeBuilder is used to deploy UltraNet and VGG networks on Ultra96-V2 FPGA in this study, and the generated UltraNet-P1 accelerator improves power consumption and energy efficiency by 17.71% and 21.54%, respectively, compared with the state-of-the-art UltraNet custom accelerator. Compared with mainstream inference frameworks, energy efficiency of the VGG accelerator generated by NN-EdgeBuilder is improved by 4.40 times and Digital Signal Processor(DSP) computing efficiency is improved by 50.65%.
-
算法1 全连接运算循环嵌套 (1) Loop1: $ \text{ for(ci=0;ci < CI;ci++)} $ (2) Loop2: $ \text{ for(co=0;co < CO;co++)} $ (3) ${ {\boldsymbol{O} }_{{\rm{fc}}} }[{\rm{co}}]$+=$ {I_{{\text{fc}}}}{\text{[ci]}} \times {F_{{\text{fc}}}}{\text{[co,ci]}} $ (4) EndLoop 算法2 卷积运算循环嵌套 (1) Loop1: $ \text{ for(wo=0;wo < WO;wo++)} $ (2) Loop2: $ \text{ for(ho=0;ho < HO;ho++)} $ (3) Loop3: $ \text{ for(co=0;co < CO;co++)} $ (4) Loop4: $ \text{ for(ci=0;ci < CI;ci++)} $ (5) Loop5: $ \text{ for(hf=0;hf < HF;hf++)} $ (6) Loop6: $ \text{ for(wf=0;wf < WF;wf++)} $ (7) ${ {\boldsymbol{O} } }_{\text{conv} }[{\rm{co}},{\rm{ho}},{\rm{wo}}]$+=${I_{ {\text{conv} } } }[{\rm{ci}},{\rm{ho} } + {\rm{hf} },$
${\rm{wo}} + {\rm{wf}}] \times{F_{ {\text{conv} } } }{\text{[co,ci,hf,wf]} }$(8) EndLoop 算法3 贝叶斯优化算法流程 输入:设计空间$F$,代理模型${ {\rm{GP}} _M}$,采集函数${{\rm{EHVIC}}}$,目标
函数${\varphi }(x)$,约束$ {C}(x) $输出:推理框架NN-EdgeBuilder自动部署的加速器设计空间的
Pareto前沿$P({{\mathcal{V} } })$(1) 在$F$内采样,得到包含$J$个样本的数据集${D_{\varphi } } = ({\boldsymbol{X}},{\boldsymbol{Y}})$,约
束集${D_{C}} = \{ {C}(x)\} $(2) while !(停止条件) do (3) 根据样本集${D_{\varphi }}$和约束集${D_{C}}$拟合代理模型${ {\rm GP} _{{M} } }$ (4) 对于$ \forall p \in {P_n} $,算出期望的超体积改进量${{\rm{EHVI}}} (x)$和满足
约束的期望${{\rm{CS}}} (p)$(5) 求出采集函数的极值${x^{J + 1} } = \arg \mathop {\max }\limits_{x \in F} {{\rm{EHVIC}}} (x)$,选择
新的采样点(6) 运行Vivado工具流得到准确的函数值${\varphi }({x^{J + 1}})$,约束
$ {C}({x^{J + 1}}) $(7) 更新数据集${D_{\varphi }}$和约束集${D_{C}}$ (8) end while (9) return加速器设计空间的Pareto前沿$ P({ {\mathcal{V} } }) $ 表 1 UltraNet加速器性能对比
加速器 IOU FPS Energy(J) GOPS GOPS/W UltraNet-P1 0.702 2107 30.2 387.7 319.9 UltraNet-P2 0.703 2090 33.0 384.6 292.8 SEUer 0.703 2020 36.7 371.7 263.2 ultrateam 0.703 2266 40.3 416.9 239.7 表 2 NN-EdgeBuilder和其他推理框架部署VGG网络的性能对比
NN-EdgeBuilder DeepBurning-SEG[6] fpgaConvNet[7] HyBridDNN[8] DNNBuilder[9] 支持的
深度学习框架PyTorch,
TensorFlow & Keras– Caffe & Torch – Caffe FPGA平台 ZU3EG ZU3EG XC7Z020 XC7Z020 XC7Z045 频率(MHz) 250 200 125 100 200 DSP 360 264 220 220 680 量化精度 4 bit 8 bit 16 bit 16 bit 8 bit GOPS 418 203 48 83 524 GOPS/DSP 1.16 0.77 0.22 0.38 0.77 GOPS/W 320.2 – 7.3 32.0 72.8 -
[1] SIMONYAN K and ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]. The 3rd International Conference on Learning Representations, San Diego, USA, 2015: 1–14. [2] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. The 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. [3] 张萌, 张经纬, 李国庆, 等. 面向深度神经网络加速芯片的高效硬件优化策略[J]. 电子与信息学报, 2021, 43(6): 1510–1517. doi: 10.11999/JEIT210002ZHANG Meng, ZHANG Jingwei, LI Guoqing, et al. Efficient hardware optimization strategies for deep neural networks acceleration chip[J]. Journal of Electronics &Information Technology, 2021, 43(6): 1510–1517. doi: 10.11999/JEIT210002 [4] ZHANG Xiaofan, LU Haoming, HAO Cong, et al. SkyNet: a hardware-efficient method for object detection and tracking on embedded systems[C]. Machine Learning and Systems, Austin, USA, 2020: 216–229. [5] LI Guoqing, ZHANG Jingwei, ZHANG Meng, et al. Efficient depthwise separable convolution accelerator for classification and UAV object detection[J]. Neurocomputing, 2022, 490: 1–16. doi: 10.1016/j.neucom.2022.02.071 [6] CAI Xuyi, WANG Ying, MA Xiaohan, et al. DeepBurning-SEG: Generating DNN accelerators of segment-grained pipeline architecture[C]. 2022 55th IEEE/ACM International Symposium on Microarchitecture (MICRO), Chicago, USA, 2022: 1396–1413. [7] VENIERIS S I and BOUGANIS C S. fpgaConvNet: Mapping regular and irregular convolutional neural networks on FPGAs[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(2): 326–342. doi: 10.1109/TNNLS.2018.2844093 [8] YE Hanchen, ZHANG Xiaofan, HUANG Zhize, et al. HybridDNN: A framework for high-performance hybrid DNN accelerator design and implementation[C]. 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, USA, 2020: 1–6. [9] ZHANG Xiaofan, WANG Junsong, ZHU Chao, et al. DNNBuilder: An automated tool for building high-performance DNN hardware accelerators for FPGAs[C]. 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Diego, USA, 2018: 1–8. [10] BANNER R, NAHSHAN Y, and SOUDRY D. Post training 4-bit quantization of convolutional networks for rapid-deployment[C]. The 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, 2019: 714. [11] DUARTE J, HAN S, HARRIS P, et al. Fast inference of deep neural networks in FPGAs for particle physics[J]. Journal of Instrumentation, 2018, 13: P07027. doi: 10.1088/1748-0221/13/07/P07027 [12] GHIELMETTI N, LONCAR V, PIERINI M, et al. Real-time semantic segmentation on FPGAs for autonomous vehicles with hls4ml[J]. Machine Learning:Science and Technology, 2022, 3(4): 045011. doi: 10.1088/2632-2153/ac9cb5 [13] ZHANG Zheng, CHEN Tinghuan, HUANG Jiaxin, et al. A fast parameter tuning framework via transfer learning and multi-objective bayesian optimization[C]. The 59th ACM/IEEE Design Automation Conference, San Francisco, USA, 2022: 133–138. doi: 10.1145/3489517.3530430. [14] HUTTER F, HOOS H H, and LEYTON-BROWN K. Sequential model-based optimization for general algorithm configuration[C]. The 5th International Conference on Learning and Intelligent Optimization, Rome, Italy, 2011: 507–523. [15] ZHAN Dawei and XING Huanlai. Expected improvement for expensive optimization: A review[J]. Journal of Global Optimization, 2020, 78(3): 507–544. doi: 10.1007/s10898-020-00923-x [16] EMMERICH M T M, DEUTZ A H, and KLINKENBERG J W. Hypervolume-based expected improvement: Monotonicity properties and exact computation[C]. 2011 IEEE Congress of Evolutionary Computation (CEC), New Orleans, USA, 2011: 2147–2154. [17] ABDOLSHAH M, SHILTON A, RANA S, et al. Expected hypervolume improvement with constraints[C]. 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 2018: 3238–3243. -





 下载:
下载:



 下载:
下载:
