Digital Twin-assisted Task Offloading Algorithms for the Industrial Internet of Things
-
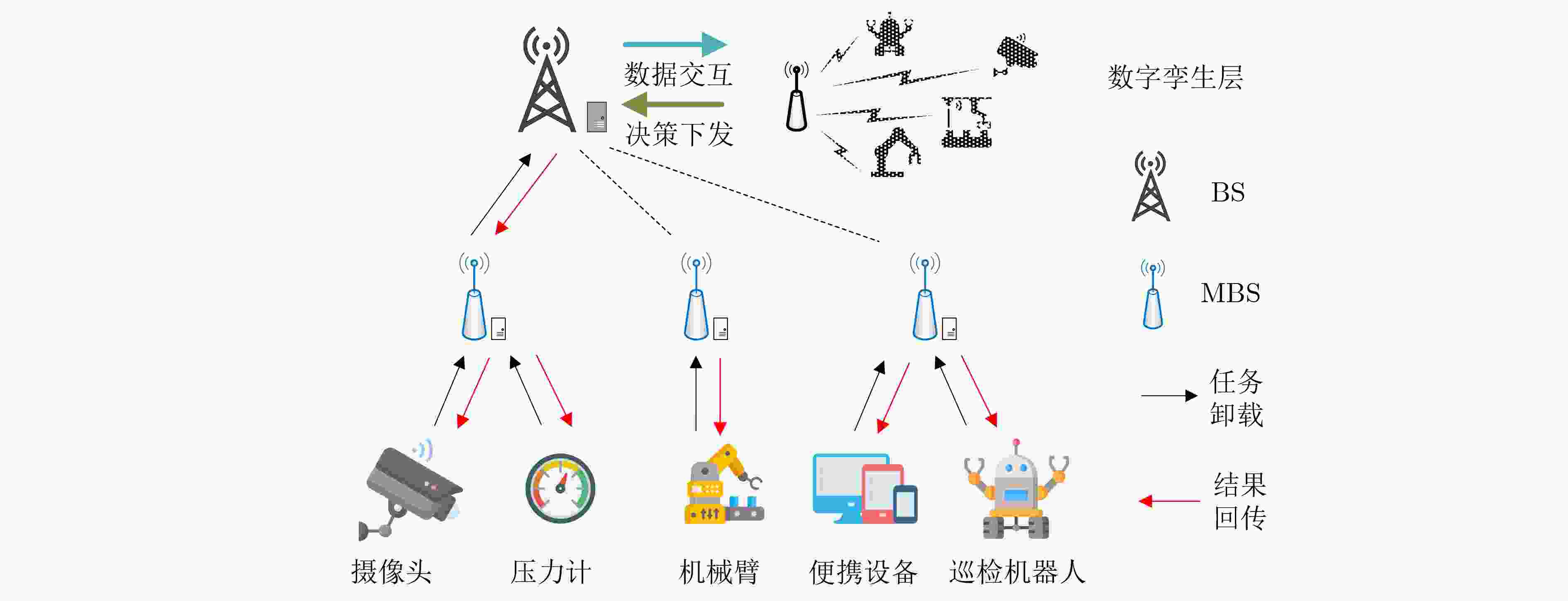
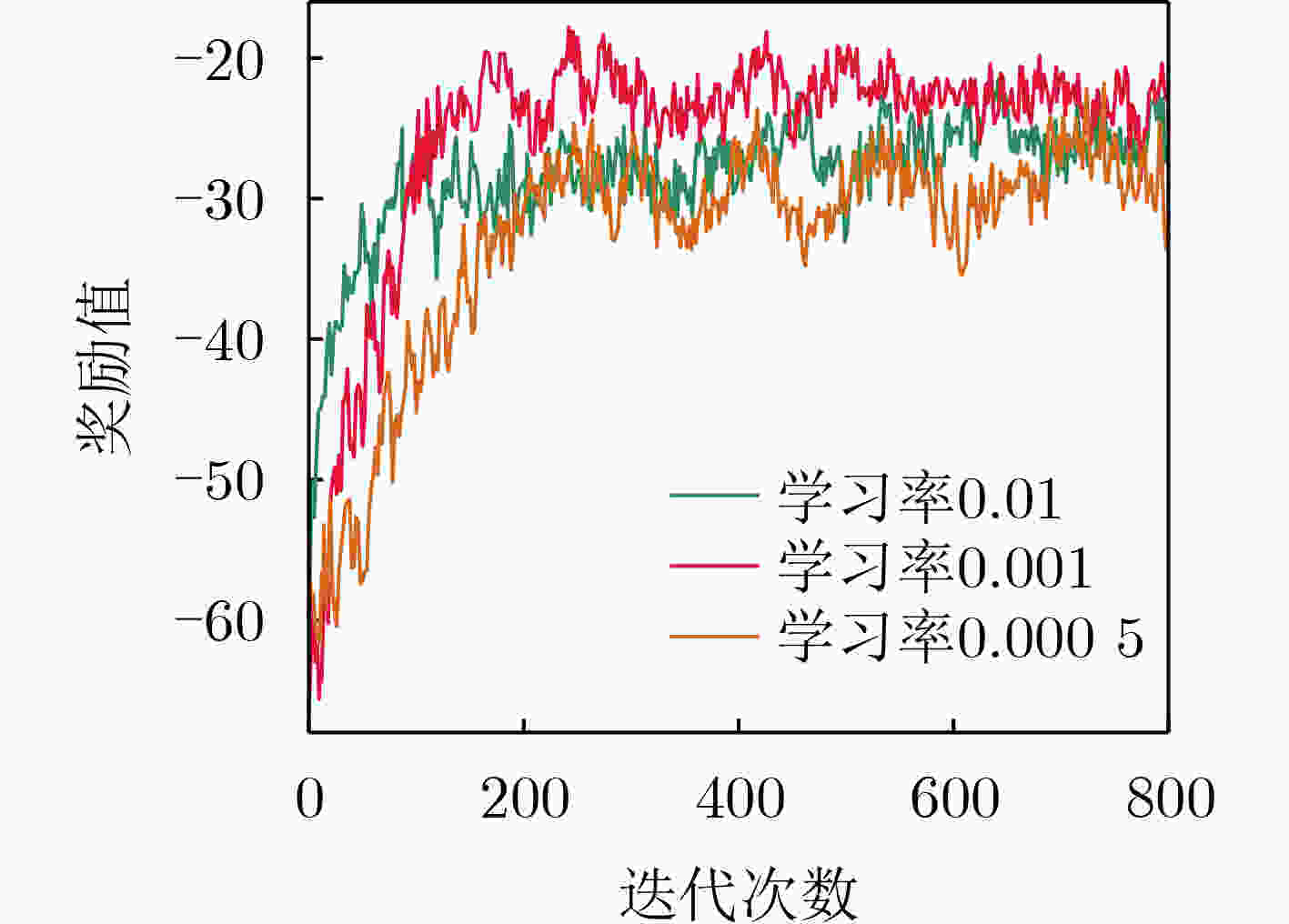
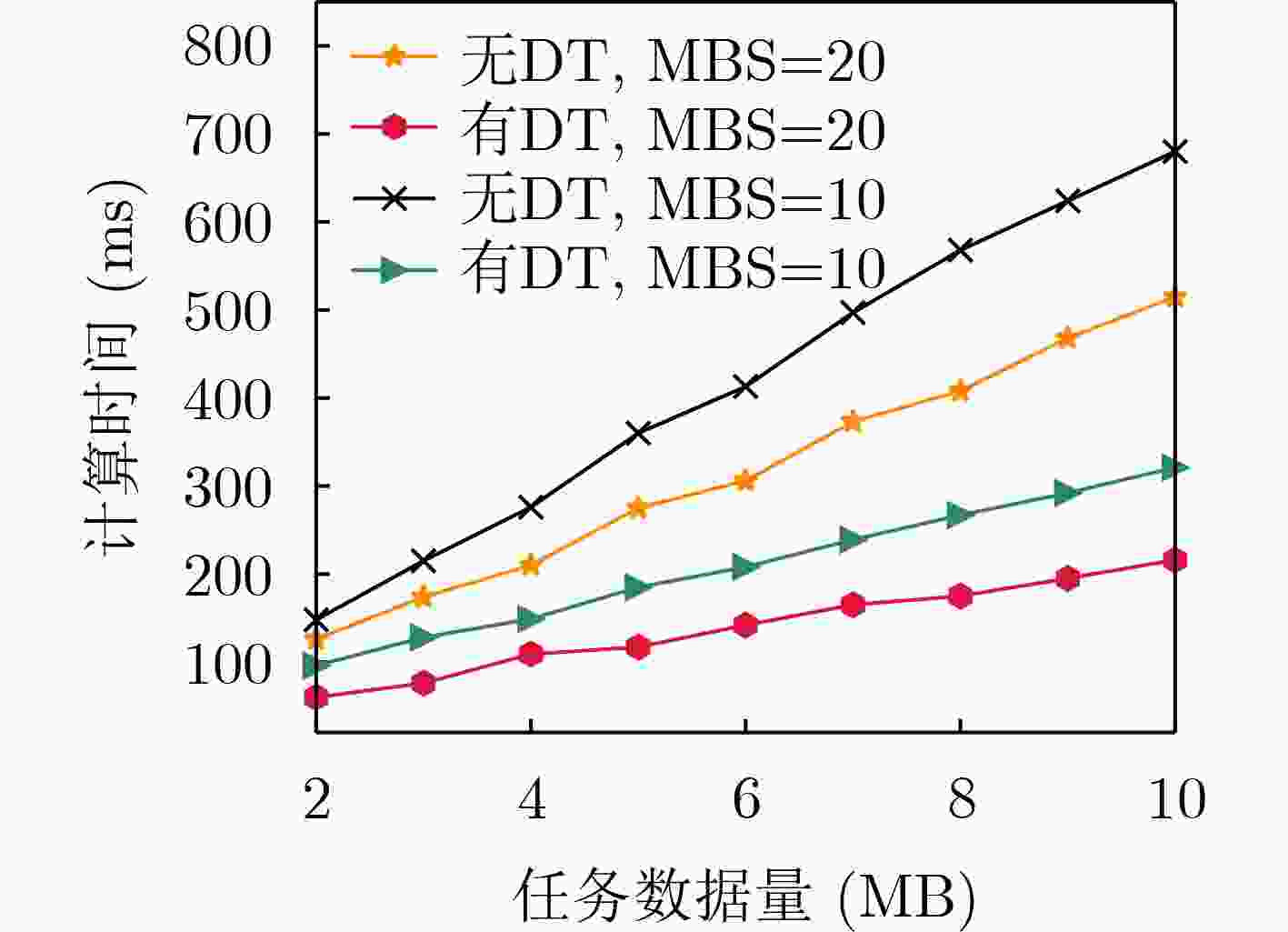
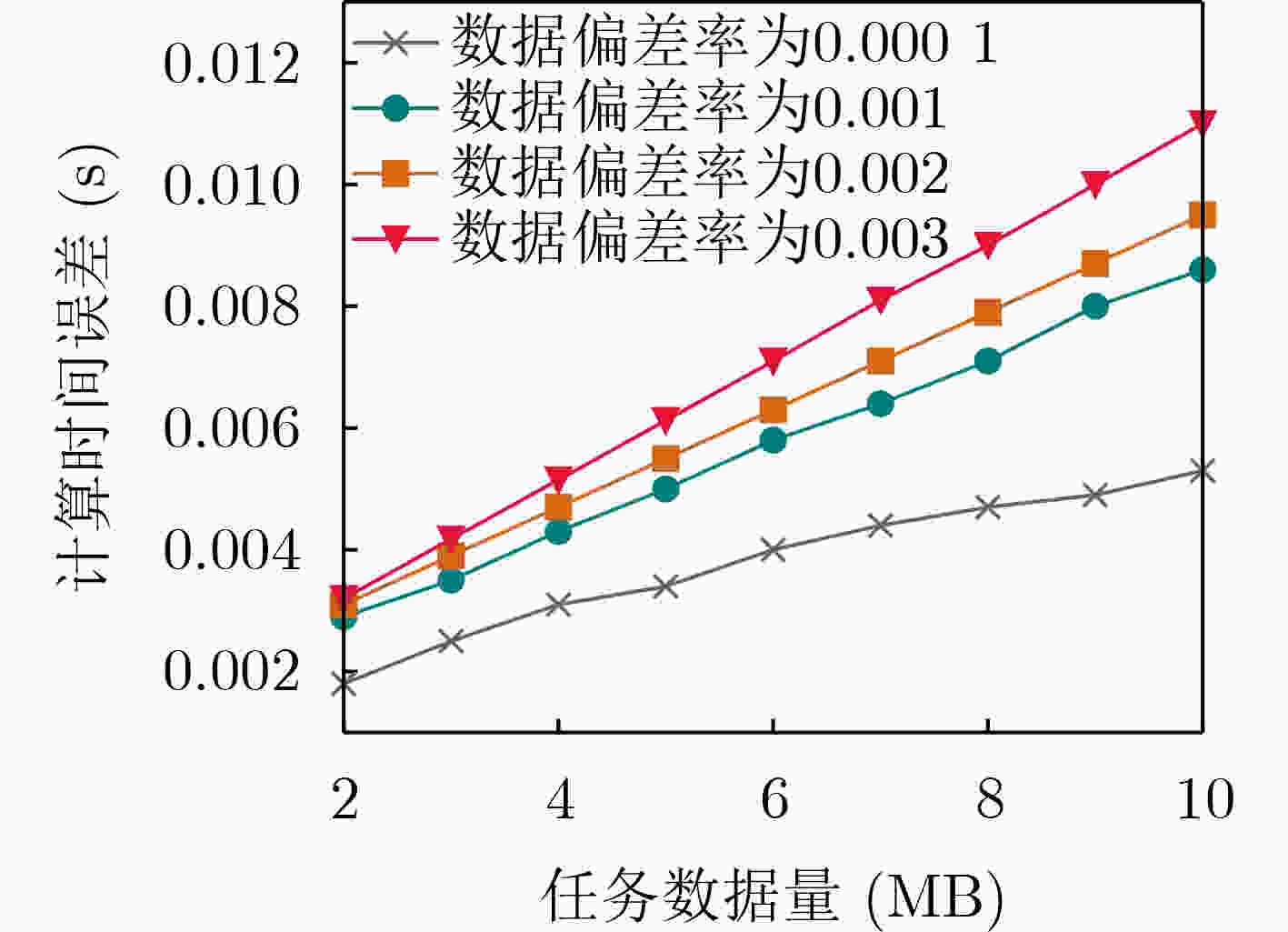
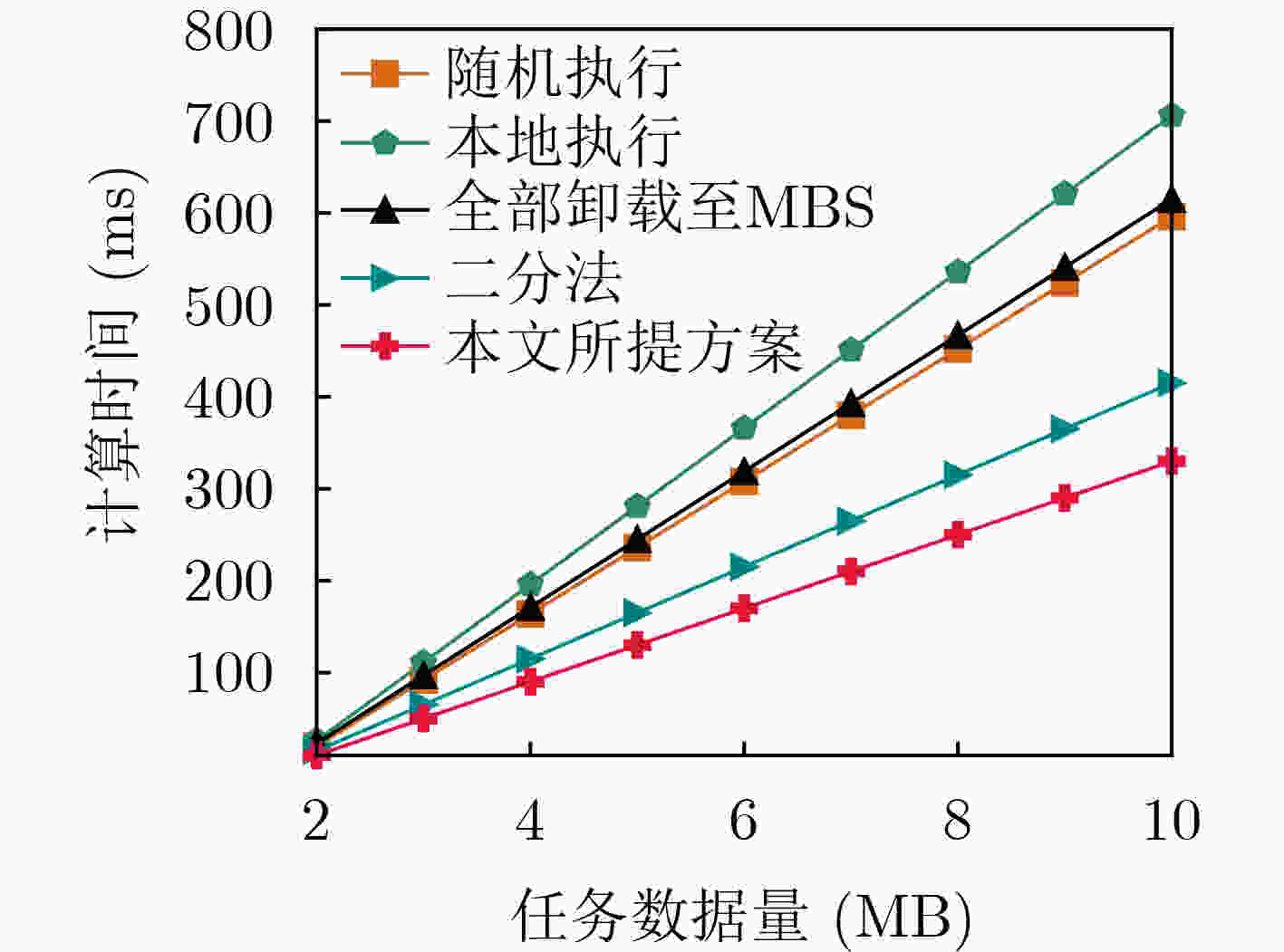
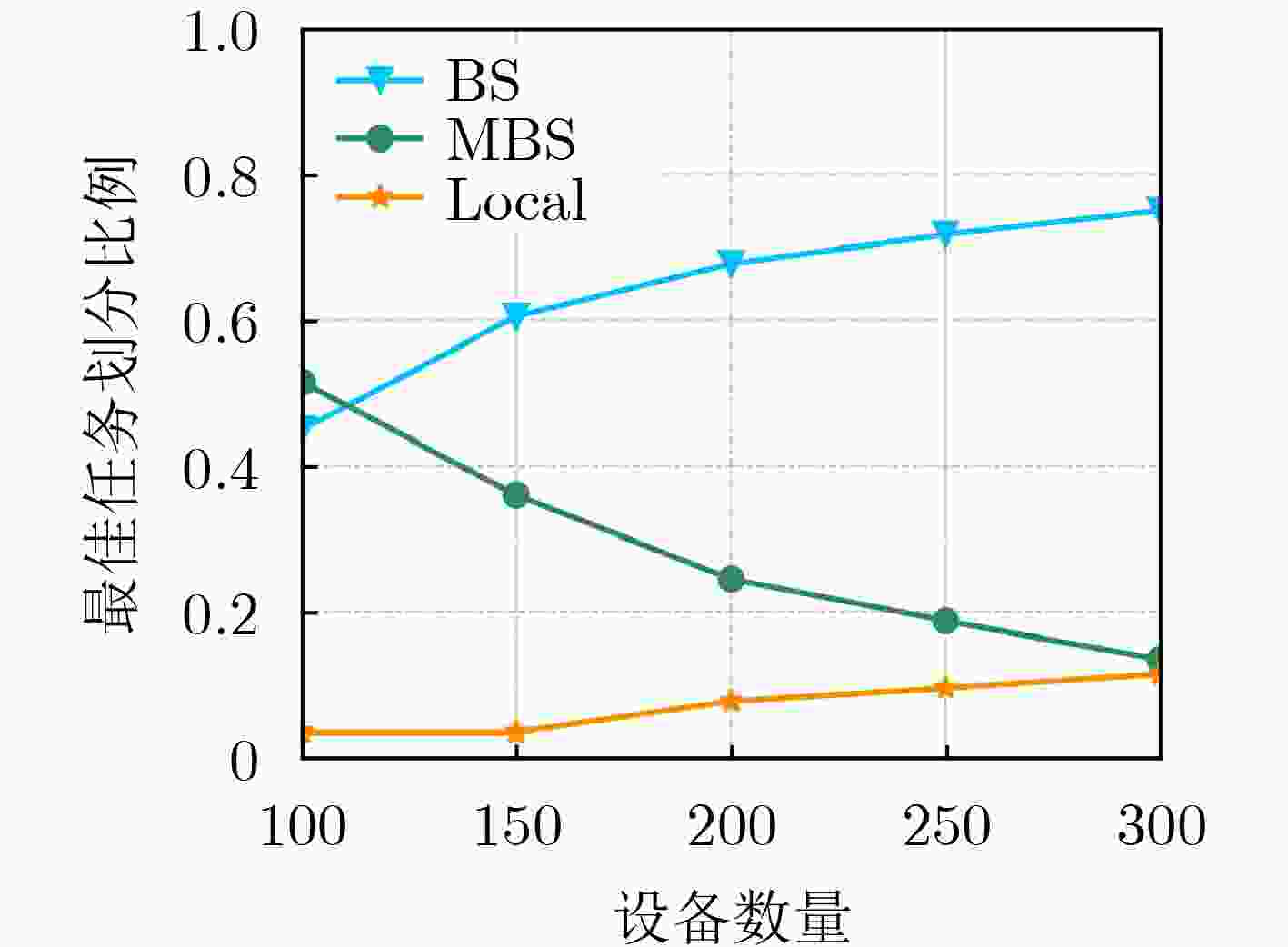
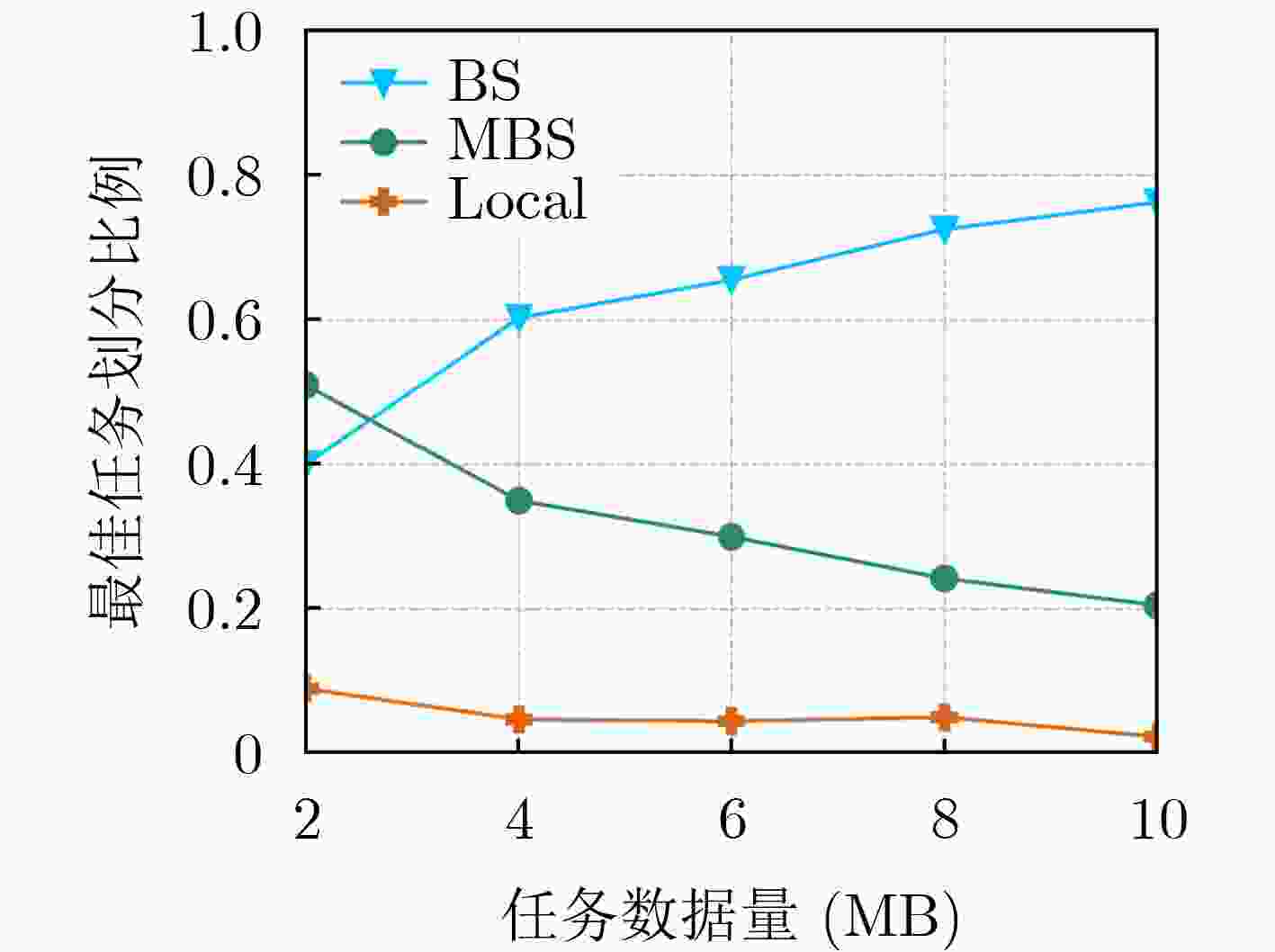
摘要: 针对工业物联网(IIoT)设备资源有限和边缘服务器资源动态变化导致的任务协同计算效率低等问题,该文提出一种工业物联网中数字孪生(DT)辅助任务卸载算法。首先,该算法构建了云-边-端3层数字孪生辅助任务卸载框架,在所创建的数字孪生层中生成近似最佳的任务卸载策略。其次,在任务计算时间和能量的约束下,从时延的角度研究了计算卸载过程中用户关联和任务划分的联合优化问题,建立了最小化任务卸载时间和服务失败惩罚的优化模型。最后,提出一种基于深度多智能体参数化Q网络(DMAPQN)的用户关联和任务划分算法,通过每个智能体不断地探索和学习,以获取近似最佳的用户关联和任务划分策略,并将该策略下发至物理实体网络中执行。仿真结果表明,所提任务卸载算法有效降低了任务协同计算时间,同时为每个计算任务提供近似最佳的卸载策略。Abstract: To address the low efficiency of task collaboration computation caused by limited resources of Industrial Internet of Things (IIoT) devices and dynamic changes of edge server resources, a Digital Twin (DT)-assisted task offloading algorithm is proposed for IIoT. First, the cloud-edge-end three-layer digital twin-assisted task offloading framework is constructed by the algorithm, and the approximate optimal task offloading strategy is generated in the created digital twin layer. Second, under the constraints of task computation time and energy, the joint optimization problem of user association and task partition in the computation offloading process is studied from the perspective of delay. An optimization model is established with the goal of minimizing the task offloading time and service failure penalty. Finally, a user association and task partition algorithm based on Deep Multi-Agent Parameterized Q-Network (DMAPQN) is proposed. The approximate optimal user association and task partition strategy is obtained by each intelligent agent through continuous exploration and learning, and it is issued to the physical entity network for execution. Simulation results show that the proposed task offloading algorithm effectively reduces the task collaboration computation time and provides approximate optimal offloading strategies for each computational task.
-
1 基于DMAPQN的用户关联和任务划分算法
输入:价值网络和策略网络的学习率$ \{ {\alpha _{k,1}},{\alpha _n},{\beta _{k,2}},{\beta _n}\} $;探索概率$ \phi $;全局学习回合数$ {J_{{\text{max}}}} $;概率分布$ \psi $;一个mini-batch中小批量数
据$ I $;采样数据学习回合数$ {I_{{\text{max}}}} $初始化:经验回放池$ \varUpsilon $,初始化全局价值函数$ Q_{{\text{tot}}}^{{\text{sum}}} $,随机初始化各个智能体中的网络参数,随机初始化全局网络参数$ {\theta _{{\text{tot}}}} $和$ {\omega _{{\text{tot}}}} $; 输出:用户关联和任务划分策略$ {{\boldsymbol{\pi}} ^*} $ (1) for $ j = 1,2,\cdots ,{J_{\max }} $ do (2) for $ n = 1,2,\cdots ,N $ do (3) for $ k = 1,2,\cdots ,K $ do (4) 根据式(29)计算连续动作$ {x_{{u_{k,n}}}} \leftarrow {x_{{u_{k,n}}}}({{\boldsymbol{s}}_{k,n}},{\theta _{k,n}},{\theta _{{\text{tot}},n}}) $ (5) 根据$ \phi $-贪婪策略选择动作$ {{\boldsymbol{a}}_{k,n}} = \{ {u_{k,n}},{x_{{u_{k,n}}}}\} $,选择原则为 $ {{\boldsymbol{a}}}_{k,n}=\left\{\begin{array}{l}来自分布\psi \text{ }的一个样本,概率\varphi \\ \{{u}_{k,n},{x}_{{u}_{k,n}}\},\;{u}_{k,n}=\mathrm{arg}\underset{{u}_{k,n}\in [{U}_{k,n}]}{\mathrm{max}}{Q}_{k,n}({{\boldsymbol{s}}}_{k,n},{u}_{k,n},{x}_{{u}_{k,n}};{\omega }_{k,n},{{\boldsymbol{\omega}} }_{n})\text{ },概率1-\varphi \end{array} \right.$ (6) 执行动作$ {{\boldsymbol{a}}_{k,n}} $,获取奖励$ {r_{k,n}} $,并观察下一个环境状态$ {{\boldsymbol{s}}_{k,n + 1}} $ (7) 将本次经验元组$ {\varUpsilon _{k,n}} = [{{\boldsymbol{s}}_{k,n}},{{\boldsymbol{a}}_{k,n}},{r_{k,n}},{{\boldsymbol{s}}_{k,n + 1}}] $存储至经验回放池中 (8) 从回放池中随机抽取经验样本$ [{{\boldsymbol{s}}_{k,i}},{{\boldsymbol{a}}_{k,i}},{r_{k,i}},{{\boldsymbol{s}}_{k,i + 1}}],i \in I $ (9) 根据式(30)计算目标函数值$ {y_{k,i}} $ (10) 使用数据$ \{ {y_{k,i}},{{\boldsymbol{s}}_{k,i}},{{\boldsymbol{a}}_{k,i}}\} ,i \in I $计算随机梯度$ {\nabla _\theta }\ell _n^\varTheta ({\theta _{k,n}}) $和$ {\nabla_\omega }\ell _n^Q{\text{(}}{\omega _{k,n}}{\text{)}} $ (11) 根据式(31)和式(32),计算确定性策略网络和价值网络的损失函数 (12) 根据式(33)和式(34),更新价值网络和策略网络的参数 (13) 将本地价值函数$ {Q_{k,n}} $值上传至全局混合网络 (14) if $ i > {I_{\max }} $then (15) 根据式(37)计算全局混合网络$ Q_{{\text{tot}}}^{{\text{sum}}} $值 (16) 根据式(38)和式(39)更新全局混合网络的参数 (17) 全局混合网络将全局网络参数下发至各个智能体中 (18) end if (19) end for (20) end for (21) end for -
[1] WU Yiwen, ZHANG Ke, and ZHANG Yan. Digital twin networks: A survey[J]. IEEE Internet of Things Journal, 2021, 8(18): 13789–13804. doi: 10.1109/JIOT.2021.3079510. [2] ZHAO Liang, HAN Guangjie, LI Zhuhui, et al. Intelligent digital twin-based software-defined vehicular networks[J]. IEEE Network, 2020, 34(5): 178–184. doi: 10.1109/MNET.011.1900587. [3] LIU Tong, TANG Lun, WANG Weili, et al. Digital-twin-assisted task offloading based on edge collaboration in the digital twin edge network[J]. IEEE Internet of Things Journal, 2022, 9(2): 1427–1444. doi: 10.1109/JIOT.2021.3086961. [4] LI Bin, LIU Yufeng, TAN Ling, et al. Digital twin assisted task offloading for aerial edge computing and networks[J]. IEEE Transactions on Vehicular Technology, 2022, 71(10): 10863–10877. doi: 10.1109/TVT.2022.3182647. [5] DAI Yueyue, ZHANG Ke, MAHARJAN S, et al. Deep reinforcement learning for stochastic computation offloading in digital twin networks[J]. IEEE Transactions on Industrial Informatics, 2021, 17(7): 4968–4977. doi: 10.1109/TII.2020.3016320. [6] YE Qiaoyang, RONG Beiyu, CHEN Yudong, et al. User association for load balancing in heterogeneous cellular networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(6): 2706–2716. doi: 10.1109/TWC. 2013.040413.120676. [7] DO-DUY T, VAN HUYNH D, DOBRE O A, et al. Digital twin-aided intelligent offloading with edge selection in mobile edge computing[J]. IEEE Wireless Communications Letters, 2022, 11(4): 806–810. doi: 10.1109/LWC.2022.3146207. [8] LI Mushu, GAO Jie, ZHAO Lian, et al. Deep reinforcement learning for collaborative edge computing in vehicular networks[J]. IEEE Transactions on Cognitive Communications and Networking, 2020, 6(4): 1122–1135. doi: 10.1109/TCCN.2020.3003036. [9] VAN HUYNH D, VAN-DINH NGUYEN, SHARMA V, et al. Digital twin empowered ultra-reliable and low-latency communications-based edge networks in industrial IoT environment[C]. ICC 2022 - IEEE International Conference on Communications, Seoul, Republic of, Korea, 2022: 5651–5656. doi: 10.1109/ICC45855.2022.9838860. [10] HU Han, WANG Qun, HU R Q, et al. Mobility-aware offloading and resource allocation in a MEC-enabled IoT network with energy harvesting[J]. IEEE Internet of Things Journal, 2021, 8(24): 17541–17556. doi: 10.1109/JIOT.2021.3081983. [11] LI Changxiang, WANG Hong, and SONG Rongfang. Intelligent offloading for NOMA-assisted MEC via dual connectivity[J]. IEEE Internet of Things Journal, 2021, 8(4): 2802–2813. doi: 10.1109/JIOT.2020.3020542. [12] HEYDARI J, GANAPATHY V, and SHAH M. Dynamic task offloading in multi-agent mobile edge computing networks[C]. 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 2019: 1–6. doi: 10.1109/GLOBECOM38437.2019.9013115. [13] LIU Zening, YANG Yang, WANG Kunlun, et al. Post: Parallel offloading of splittable tasks in heterogeneous fog networks[J]. IEEE Internet of Things Journal, 2020, 7(4): 3170–3183. doi: 10.1109/JIOT.2020.2965566. [14] FU Haotian, TANG Hongyao, HAO Jianye, et al. Deep multi-agent reinforcement learning with discrete-continuous hybrid action spaces[C]. The Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 2019: 2329–2335. doi: 10.24963/IJCAI.2019/323. [15] XIONG Jiechao, WANG Qing, YANG Zhouran, et al. Parametrized deep Q-networks learning: Reinforcement learning with discrete-continuous hybrid action space[EB/OL].https://arxiv.org/abs/1810.06394, 2018. [16] SALEEM U, LIU Y, JANGSHER S, et al. Latency minimization for D2D-enabled partial computation offloading in mobile edge computing[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 4472–4486. doi: 10.1109/TVT.2020.2978027. [17] MOURAD A, TOUT H, WAHAB O A, et al. Ad hoc vehicular fog enabling cooperative low-latency intrusion detection[J]. IEEE Internet of Things Journal, 2021, 8(2): 829–843. doi: 10.1109/JIOT.2020.3008488. -





 下载:
下载:


 下载:
下载:
