Research on Low-overhead Dual-output XOR Gate True Random Number Generator Utilizing Fine-grained Sampling
-
摘要: 真随机数生成器(TRNG)是安全应用中的关键构建模块,能够为数据加密、随机数和初始化向量提供高质量的随机位。环形振荡器(RO)TRNG是一种广泛的应用设计,以支持各种与安全相关的应用。但是,在FPGA中实现RO TRNG时通常会产生很高的硬件开销。因此,一种基于双输出异或门单元的低开销RO TRNG在该文中被提出,仅使用单个可配置逻辑块即可构建TRNG的熵源。通过多相位细粒度采样机制,将电路抖动有效地采集捕捉到。所提RO TRNG在AMD Xilinx Viretx-6和Artix-7两款FPGA上进行实现与验证,实验结果表明,所提RO TRNG硬件开销低,能够产生质量满意的随机序列。Abstract: True Random Number Generator (TRNG) is a key building block in security applications that provides the required high-quality random bits for data encryption, cryptographic random numbers, and initialization vectors. The Ring Oscillator (RO) TRNG is a broad application design to support a variety of safety-related applications. However, implementing RO TRNG in FPGAs incurs typically high hardware overhead. Therefore, a low-overhead RO TRNG based on a dual-output XOR gate unit is proposed in this paper, and the entropy source circuit of TRNG can be constructed using only a single configurable logic block. Through the multi-phase fine-grained sampling mechanism, circuit jitter is effectively collected and captured. The proposed RO TRNG is implemented and verified on AMD Xilinx Viretx-6 and Artix-7 series FPGAs, and the experimental results show that the proposed RO TRNG hardware overhead is low and the quality of the random sequence is satisfactory.
-
Key words:
- True Random Number Generator(TRNG) /
- Fine-grained sampling /
- Low overhead
-
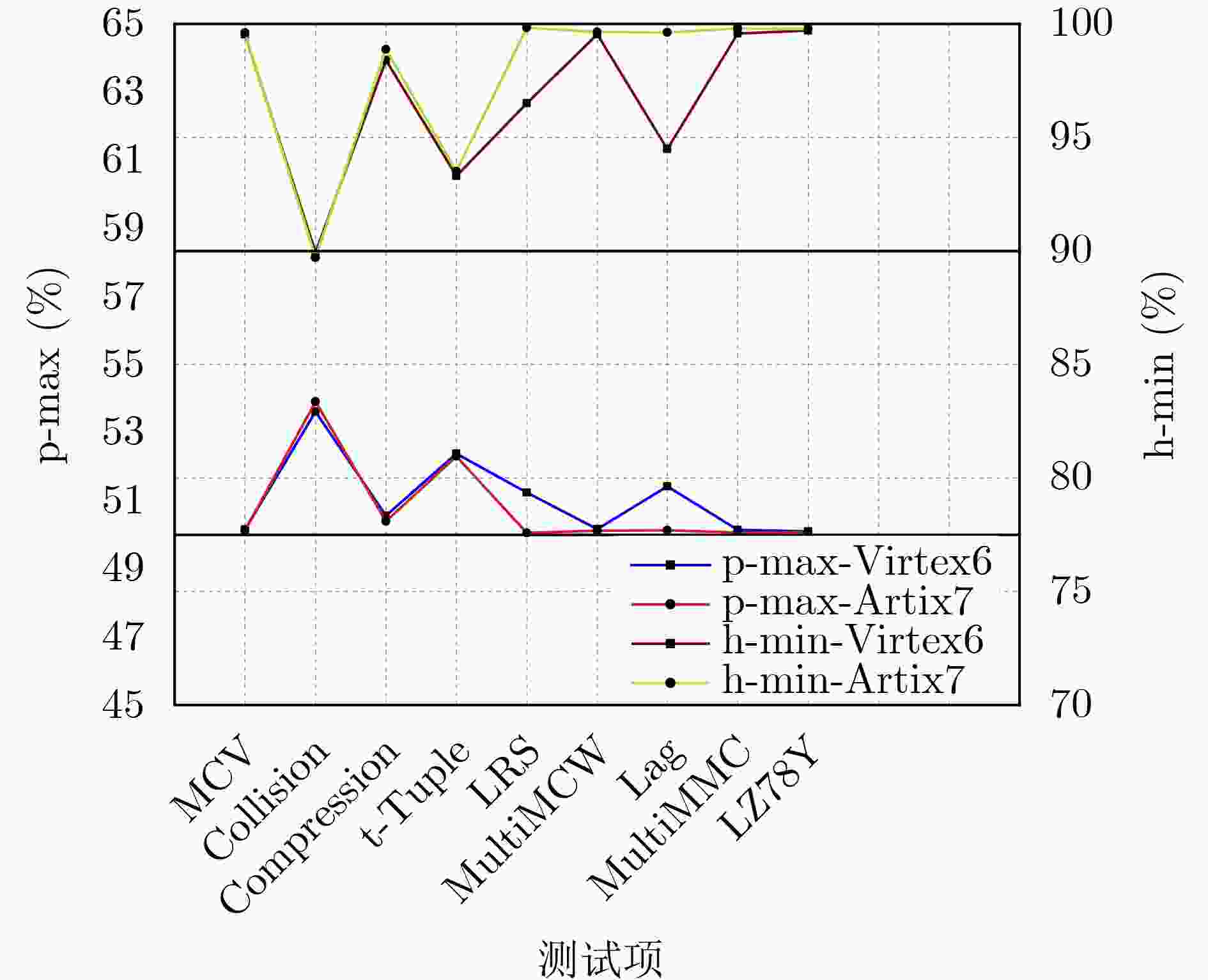
表 1 Xilinx Virtex-6和Artix-7上NIST SP800-22测试结果
NIST
随机性测试项Virtex-6 FPGA Artix-7 FPGA P-value Prop.(%) P-value Prop(%) 频率检验 0.496 605 100 0.417146 100 累加和检验 0.607 715 100 0.557145 100 块内频数检验 0.470 025 100 0.341 223 99 游程检验 0.717 631 99 0.544 285 100 块内最长游程检测 0.360 79 100 0.439 515 98 2元矩阵秩检验 0.166 805 100 0.636 792 99 离散傅里叶变换检验 0.588 595 98 0.409 091 100 非重叠模块匹配检测 0.452 413 99 0.452 517 100 重叠模块匹配检验 0.480 335 100 0.544 095 99 通用统计检验 0.395 355 100 0.678 435 98 近似熵检验 0.329 119 99 0.439 280 100 随机游动检验 0.300 740 100 0.482 493 99 随机游动状态频数检验 0.420 495 99 0.480 785 100 序列检验 0.246 073 100 0.186 504 100 线性复杂度检验 0.430 225 100 0.419 696 100 表 2 AIS-31的T8字节熵测试
开发套件 Virtex-6 Artix-7 熵值 7.998671 7.996367 -
[1] HASSIJA V, CHAMOLA V, GUPTA V, et al. A survey on supply chain security: Application areas, security threats, and solution architectures[J]. IEEE Internet of Things Journal, 2021, 8(8): 6222–6246. doi: 10.1109/JIOT.2020.3025775 [2] 魏子魁, 胡毅, 金鑫, 等. 一种低功耗高噪声源真随机数设计[J]. 电子与信息学报, 2020, 42(10): 2566–2572. doi: 10.11999/JEIT190719WEI Zikui, HU Yi, JIN Xin, et al. A true random number design of low power and high noise source[J]. Journal of Electronics &Information Technology, 2020, 42(10): 2566–2572. doi: 10.11999/JEIT190719 [3] LU Yingchun, LIANG Huaguo, YAO Liang, et al. Jitter-quantizing-based TRNG robust against PVT variations[J]. IEEE Access, 2020, 8: 108482–108490. doi: 10.1109/ACCESS.2020.3000231 [4] RUKHIN A, SOTO J, NECHVATAL J, et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications[R]. NIST Special Publication 800-22, 2010. [5] BARKER E, KELSEY J, and SECRETARY J B. NIST DRAFT special publication 800–90B recommendation for the entropy sources[OL]. https://www.nist.gov/news-events/news/2018/01/nist-announces-release-special-publication-800-906-recommendation-entropy. [6] KILLMANN W and SCHINDLE W. A proposal for: Functionality classes for random number generators[EB/OL]. https://www.bsi.bund.de/SharedDocs/Downloads/DE/BSI/Zertifizierung/Interpretationen/AIS_31_Functionality_classes_for_random_number_generators_e.html, 2011. [7] GRUJIC M and VERBAUWHEDE I. TROT: A three-edge ring oscillator based true random number generator with time-to-digital conversion[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2022, 69(6): 2435–2448. doi: 10.1109/TCSI.2022.3158022 [8] NALLA ANANDAKUMAR N, SANADHYA S K, and HASHMI M S. FPGA-based true random number generation using programmable delays in oscillator-rings[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2020, 67(3): 570–574. doi: 10.1109/TCSII.2019.2919891 [9] FRUSTACI F, SPAGNOLO F, PERRI S, et al. A high-speed FPGA-based true random number generator using metastability with clock managers[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2023, 70(2): 756–760. doi: 10.1109/TCSII.2022.3211278 [10] ZHU Shaofeng, XI Wei, FAN Limin, et al. Sequence-oriented stochastic model of RO-TRNGs for entropy evaluation[J]. Chinese Journal of Electronics, 2020, 29(2): 371–377. doi: 10.1049/cje.2019.12.010 [11] WOLD K and PETROVIĆ S. Behavioral model of TRNG based on oscillator rings implemented in FPGA[C]. 14th IEEE International Symposium on Design and Diagnostics of Electronic Circuits and Systems, Cottbus, Germany, 2011: 163–166. [12] YAO Liang, LIANG Huaguo, ZHANG Hong, et al. A lightweight M_TRNG design based on MUX cell entropy using multiphase sampling[C]. 2022 Asian Hardware Oriented Security and Trust Symposium (AsianHOST), Singapore, 2022: 1–4. [13] LI Xinwei, SHEN Lei, and ZHAO Zhijin. Jitter test of multiphase DTTL[J]. Physics Procedia, 2012, 25: 623–629. doi: 10.1016/j.phpro.2012.03.135 [14] CUI Jianguo, YI Maoxiang, CAO Di, et al. Design of true random number generator based on multi-stage feedback ring oscillator[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2022, 69(3): 1752–1756. doi: 10.1109/TCSII.2021.3111049 [15] XILINX. Virtex-6 FPGA configurable logic block[R]. UG364 (v1.2), 2012. [16] 罗芳, 欧庆于, 周学广, 等. 故障扰动下振荡环型真随机数发生器安全特性及度量方法研究[J]. 电子与信息学报, 2022, 44(6): 2093–2100. doi: 10.11999/JEIT210328LUO Fang, OU Qingyu, ZHOU Xueguang, et al. Research on the security characteristic and metric method for ring oscillatro-based true random number generator under fault disturbance[J]. Journal of Electronics &Information Technology, 2022, 44(6): 2093–2100. doi: 10.11999/JEIT210328 [17] MA Gaoliang, LIANG Huaguo, YAO Liang, et al. A low-cost high-efficiency true random number generator on FPGAs[C]. 2018 IEEE 27th Asian Test Symposium (ATS), Hefei, China, 2018: 54–58. [18] MARTIN H, PERIS-LOPEZ P, TAPIADOR J E, et al. A new TRNG based on coherent sampling with self-timed rings[J]. IEEE Transactions on Industrial Informatics, 2016, 12(1): 91–100. doi: 10.1109/TII.2015.2502183 [19] DI PATRIZIO STANCHIERI G, DE MARCELLIS A, PALANGE E, et al. A true random number generator architecture based on a reduced number of FPGA primitives[J]. AEU - International Journal of Electronics and Communications, 2019, 105: 15–23. doi: 10.1016/j.aeue.2019.03.006 [20] WANG Yonggang, HUI Cong, LIU Chong, et al. Theory and implementation of a very high throughput true random number generator in field programmable gate array[J]. Review of Scientific Instruments, 2016, 87(4): 044704. doi: 10.1063/1.4945564 [21] DEMIR K and ERGUN S. Random number generators based on irregular sampling and Fibonacci-Galois ring oscillators[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2019, 66(10): 1718–1722. doi: 10.1109/TCSII.2019.2933280 -





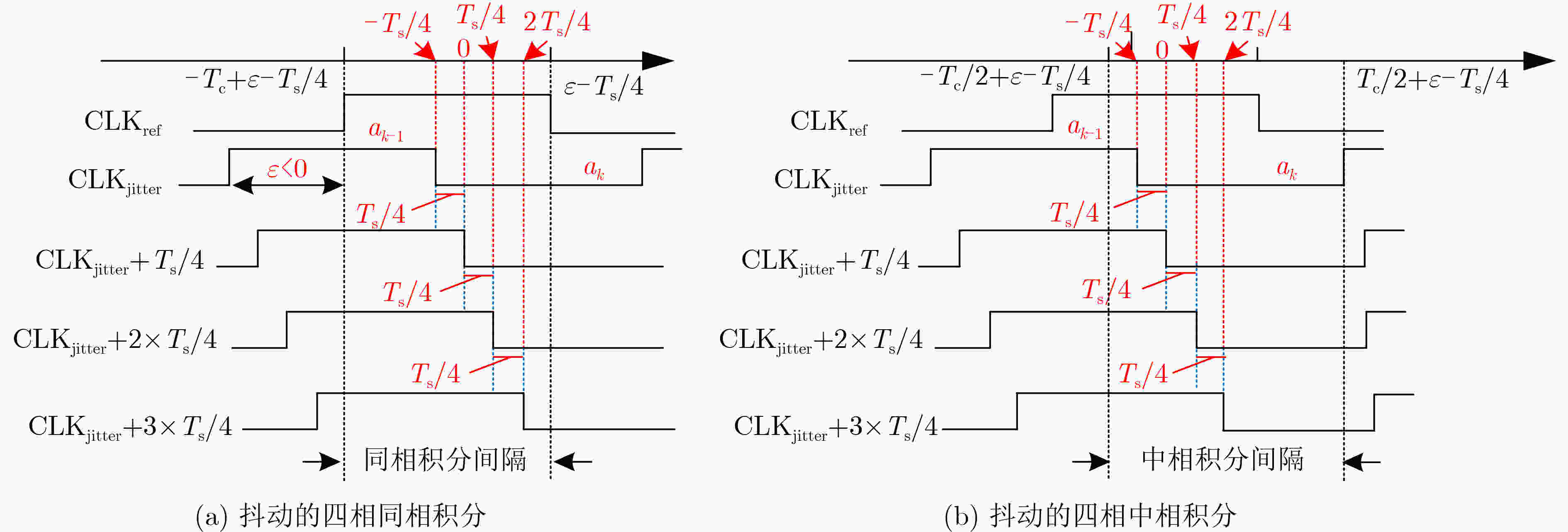
 下载:
下载:
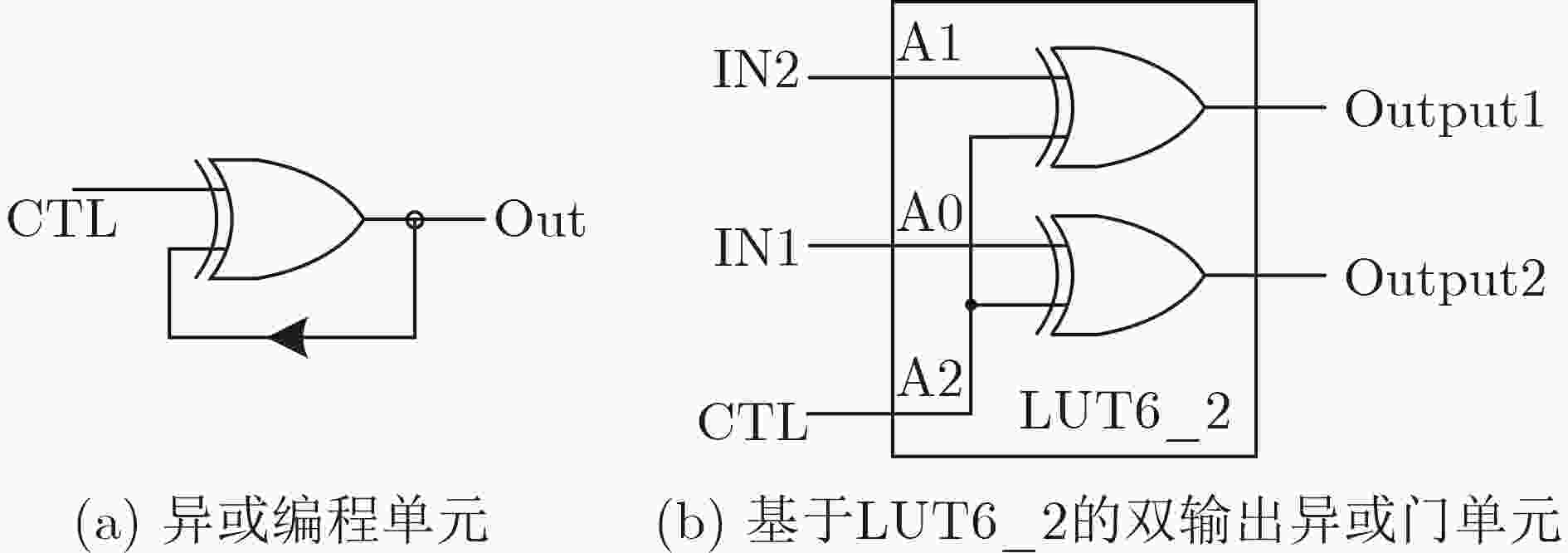
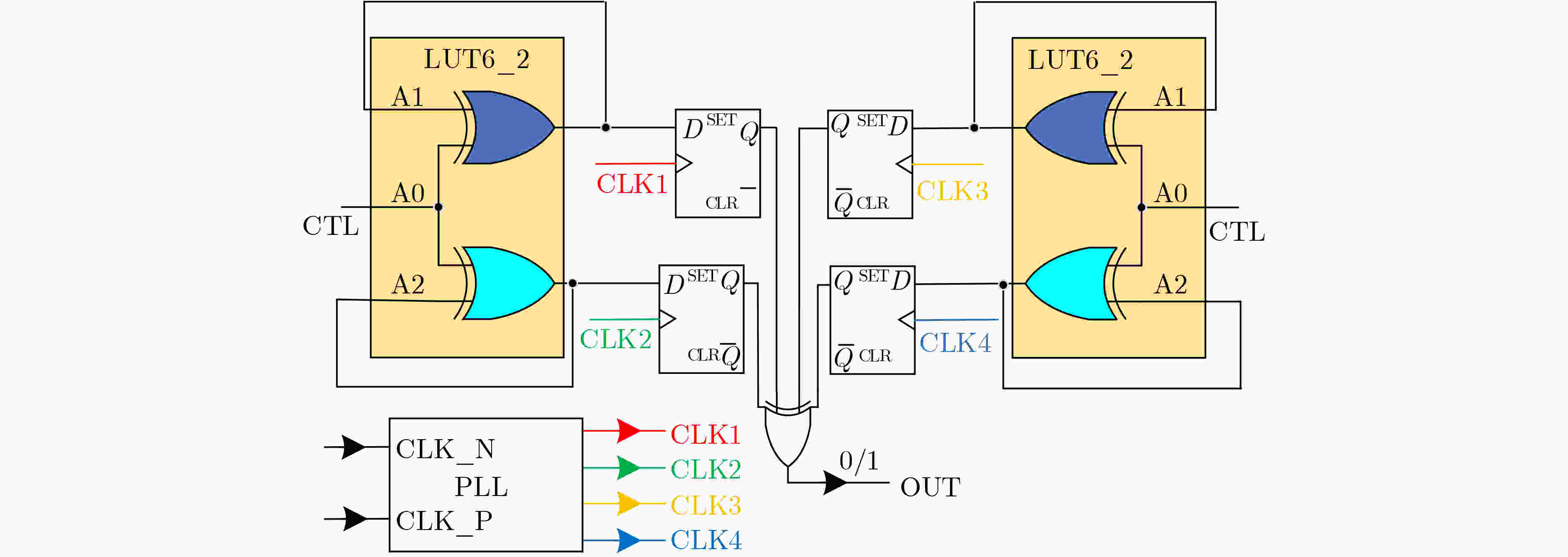
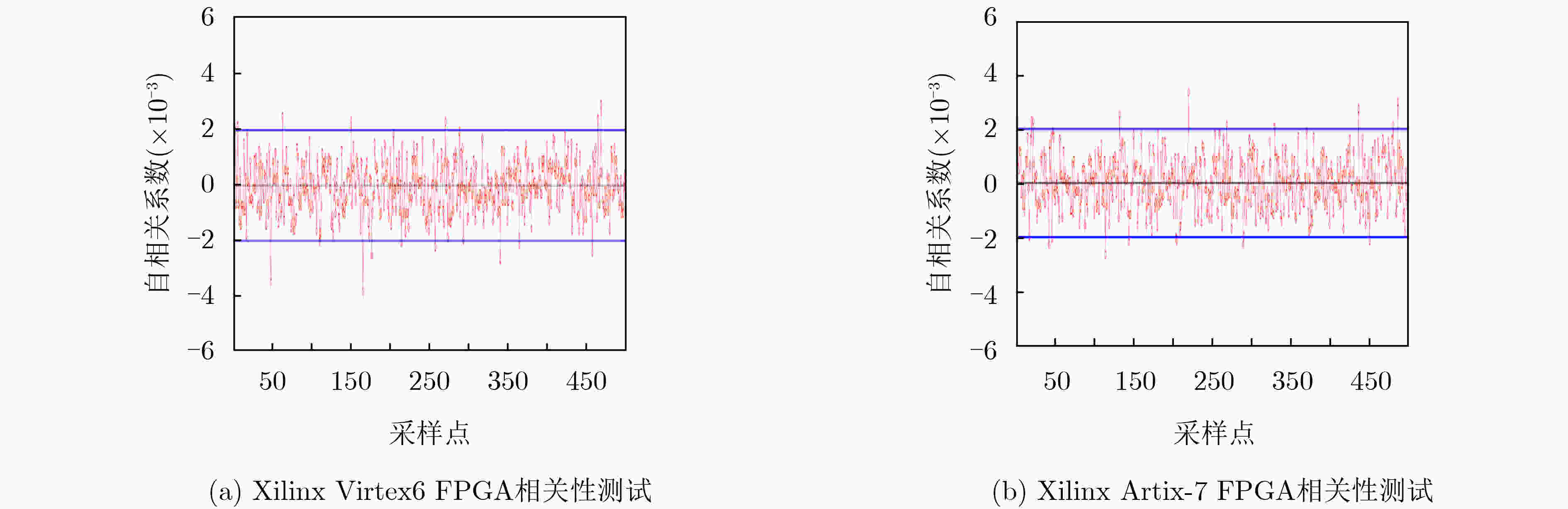
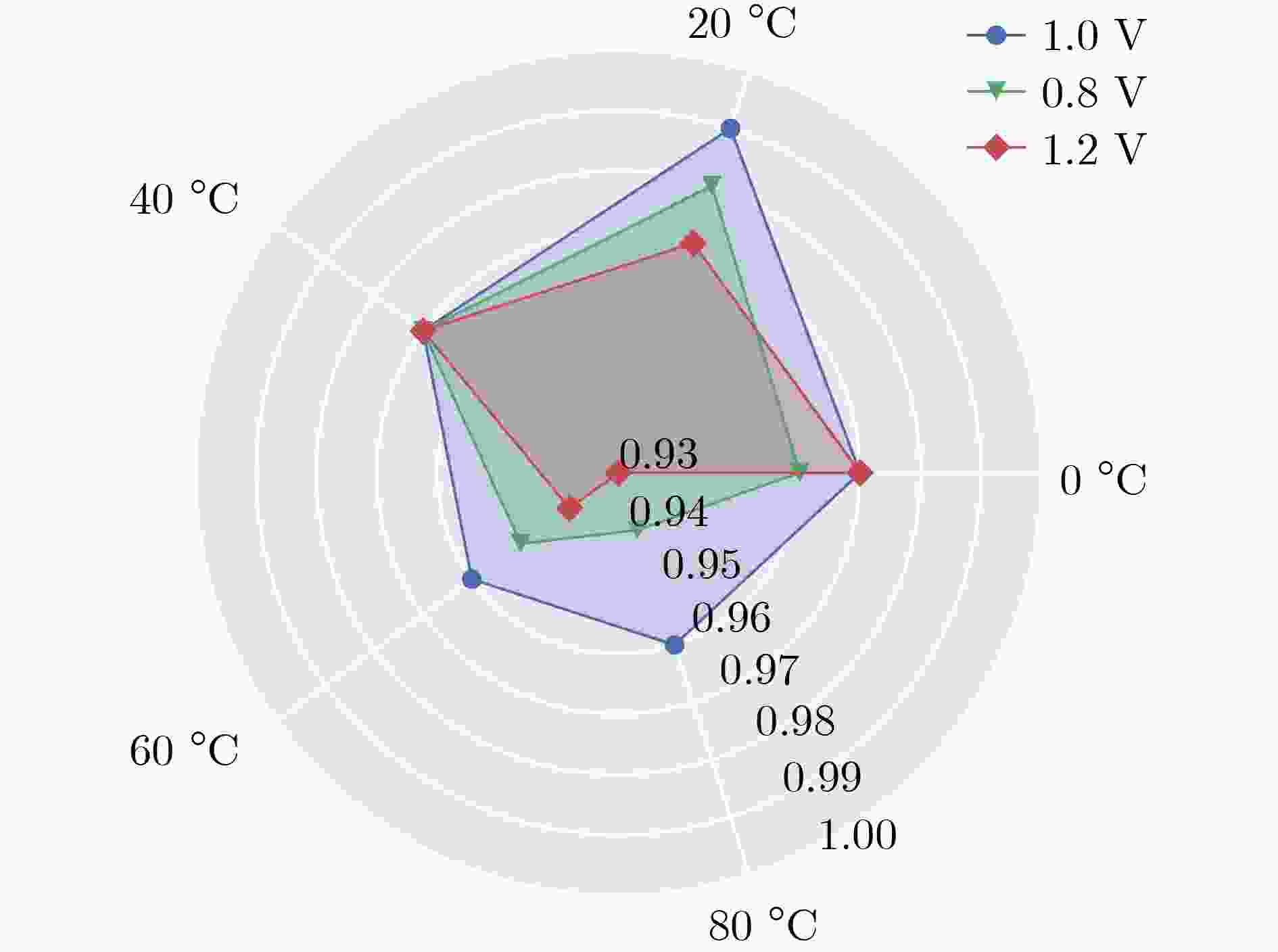


 下载:
下载:
