Reconfigurable Polynomial Multiplication Architecture for Lattice-based Post-quantum Cryptography Algorithms
-
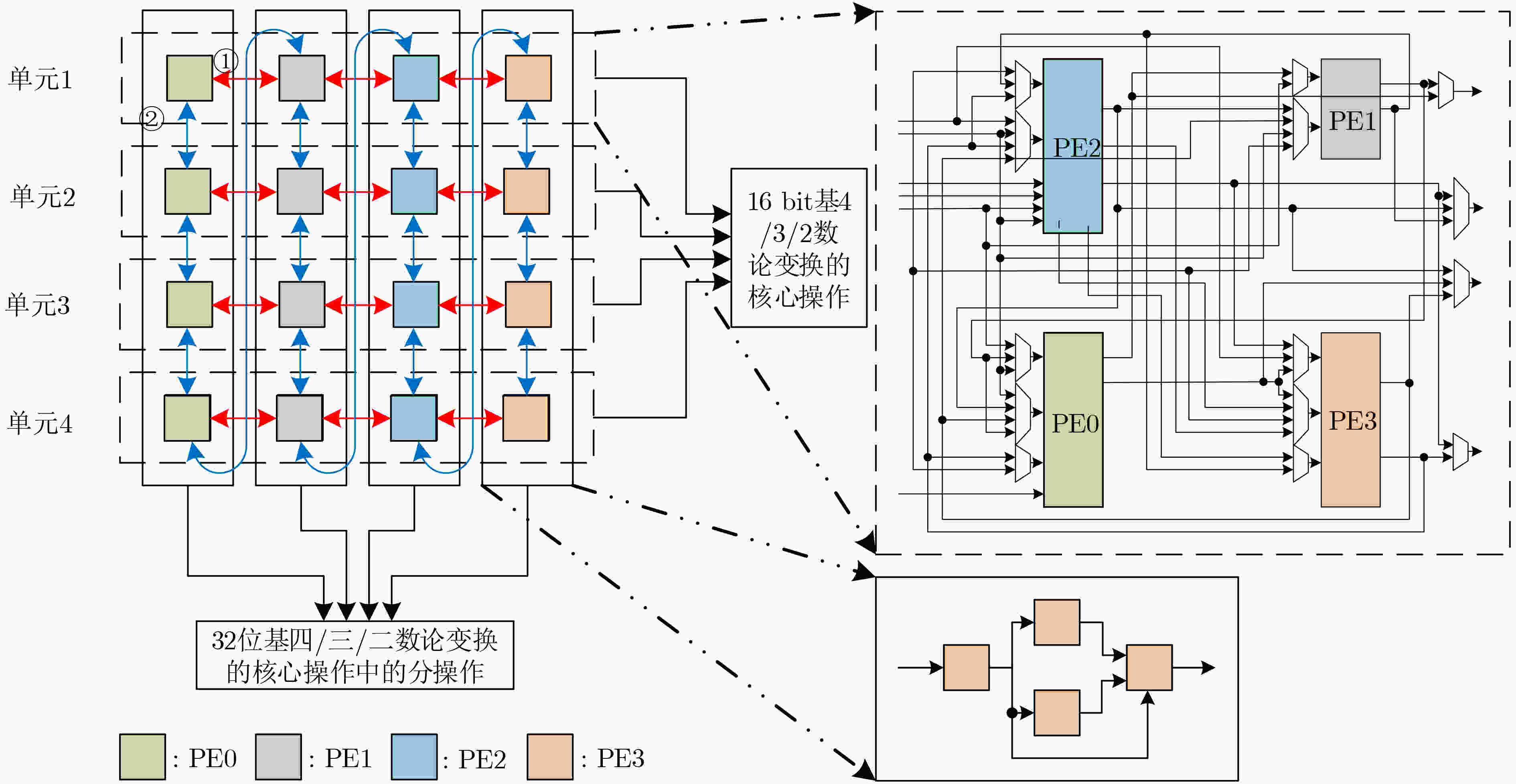
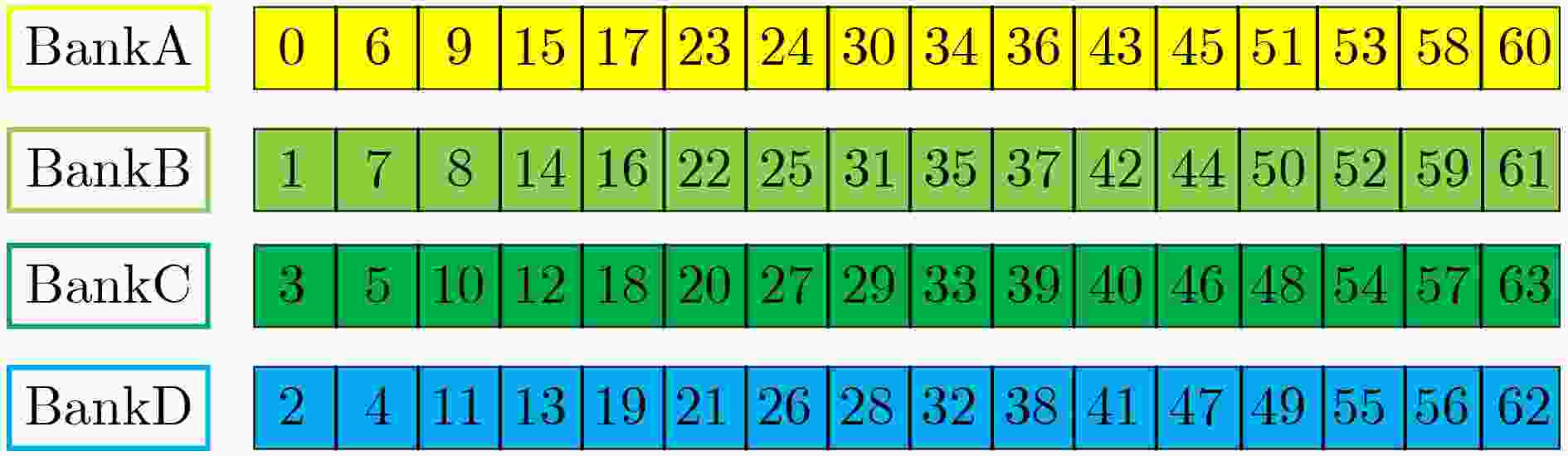
摘要: 针对基于不同困难问题格基密码算法中的多项式乘法参数各异且实现架构不统一的现状,该文提出一种基于预处理型数论变换(PtNTT)算法的可重构架构。首先进行多项式乘法运算特征分析,综合了多项式参数(项数、模数及模多项式)对可重构架构的影响。其次,针对不同项数和模多项式设计了4×4串并行可转换型运算单元架构,可满足实现不同位宽基k-数论变换的可扩展设计。其中具体针对不同模数设计了可扩展实现16 bit模乘和32 bit乘法的可重构单元。在数据需求分析过程中,通过构建以系数地址生成、Bank划分以及实际与虚拟地址对应逻辑为主体的分配机制,设计了一种满足基k-数论变换的多Bank存储结构。实验结果表明,该文支持实现Kyber, Saber, Dilithium与NTRU等4种类型算法中的多项式乘法,与其余可重构架构相比,可采用统一架构实现4种算法中的多项式乘法。基于Xilinx Artix-7 FPGA 1.599 μs完成一组项数为256,模数为3329的多项式乘法运算,花费243个时钟。Abstract: Focusing on the current situation that polynomial multiplication parameters in lattice-based cryptography algorithms with different difficult problems and the implementation architecture are not uniform, a reconfigurable architecture based on Preprocess-then-Number Theoretic Transformation (PtNTT) algorithm is proposed. Firstly, the influence of polynomial parameters (number of items, modulus and modulus polynomial) on reconfigurable architecture is integrated by analyzing the characteristics of polynomial multiplication. Secondly, a 4×4 series of parallel convertible arithmetic unit architecture is designed for different terms and modular polynomials, which can meet the scalable design of different bit width k-based number theory transformations. Specifically, a reconfigurable unit that can realize 16-bit modular multiplication and 32-bit multiplication is designed for different modules. In the process of data demand analysis, a multi-bank storage structure satisfying the k-based number theory transformation is designed by constructing a distribution mechanism based on coefficient address generation, bank division and actual and virtual address correspondence logic. Experimental results show that this paper supports the implementation of polynomial multiplication in the four types of algorithms Kyber, Saber, Dilithium and NTRU.The polynomial multiplication operation in the four algorithms can be realized by using a unified architecture compared with the other reconfigurable architectures. A set of polynomial multiplication operations with 256 terms and a modulus of 3329 can be completed at 1.599 μs, consuming 243 clocks on Xilinx Artix-7 FPGA platform.
-
表 1 适于可重构架构的多项式乘法参数
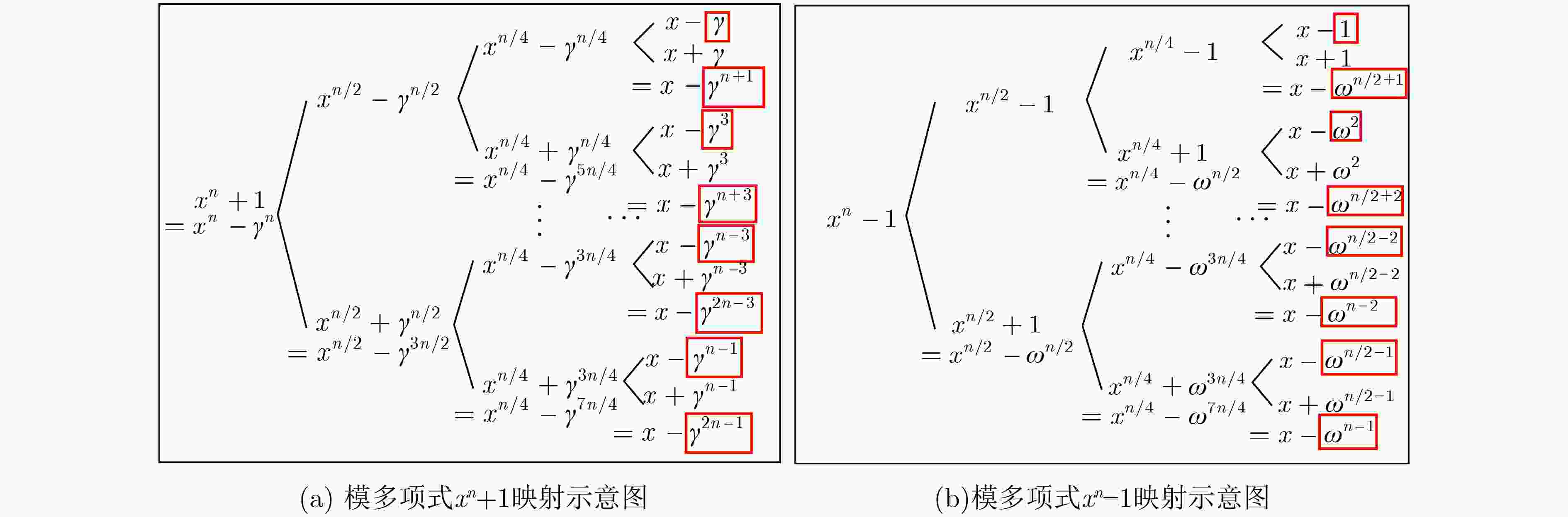
算法 项数n 模数q 模多项式 原始 扩展 原始 扩展 Kyber 256 256 3329 3329 xn+1 Saber 256 256 213 10753 xn+1 Dilithium 256 256 8380417 8380417 xn+1 NTRU NTRUhps2048509 509 1024 211 1043969 ${{\left( {{x^n} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{x^n} - 1} \right)} {\left( {x - 1} \right)}}} \right. } {\left( {x - 1} \right)}}$
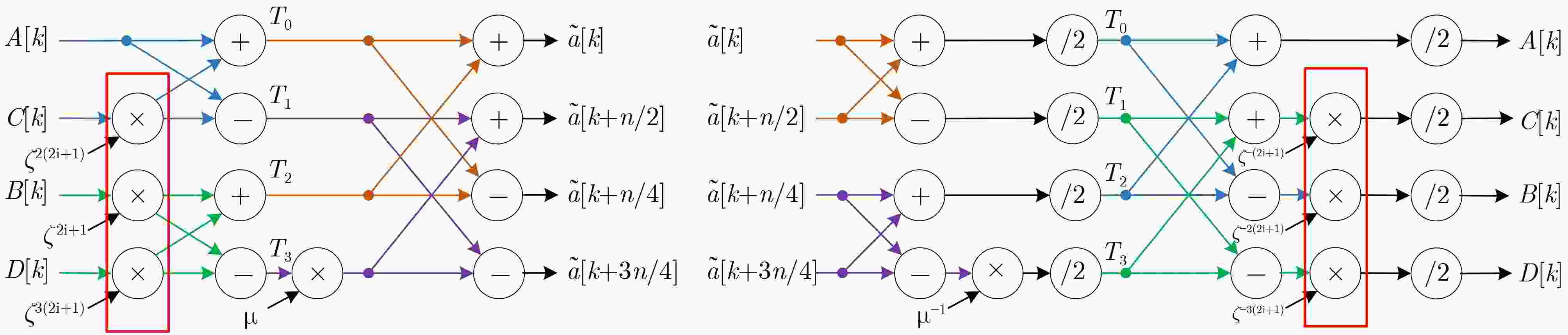
=xn–1+xn-2+···+1或xn–1NTRUhps2048677 677 1536 211 1389569 NTRUhps4096821 821 1728 212 3365569 NTRUhrss701 701 1536 213 5747201 算法1 NTRUhps4096821采用混合基PtNTT的多项式乘法 输入:a(x),b(x)$ {{ \in {Z_q}} \mathord{\left/ {\vphantom {{ \in {Z_q}} {\left( {{x^n} - 1} \right)}}} \right. } {\left( {{x^n} - 1} \right)}} $,模数q,项数n 输出:c(x)$ {{ \in {Z_q}} \mathord{\left/ {\vphantom {{ \in {Z_q}} {\left( {{x^n} - 1} \right)}}} \right. } {\left( {{x^n} - 1} \right)}} $ 1.a(x)[i]转换为3维系数f[i/192][(imod192)/3][imod3] 2.b(x)[i]转换为3维系数g[i/192][(imod192)/3][imod3] 3.for j=0; j<64; j++ for k=0; k<4; k++ $ \widehat a = {\text{NTT(}}f[0 - 8][j][k]{\text{)}} $ $ \widehat b = {\text{NTT(}}g[0 - 8][j][k]{\text{)}} $ end for end for 4.for l=0; l<9; l++ for k=0; k<4; k++ $ \widehat a = {\text{NTT(}}f[l][0 - 63][k]{\text{)}} $ $ \widehat b = {\text{NTT(}}g[l][0 - 63][k]{\text{)}} $ end for end for 5.for i=0; i<4; i++ for j=0; j<4; j++ $ {R_{i,j}} = \widehat a{\text{[0 - 8][0 - 63][}}i{\text{]}} \circ \widehat b{\text{[0 - 8][0 - 63][}}j{\text{]}} $ end for end for 6.$ \widehat {{c_0}}(x) = {R_{0,0}} + \widehat x \circ \left( {{R_{1,3}} + {R_{3,1}} + {R_{2,2}}} \right) $ $ \widehat{{c}_{1}}(x)={R}_{0,1}+{R}_{1,0}+\widehat{x}\circ ({R}_{2,3}+{R}_{3,2}) $ $ \widehat {{c_2}}(x) = {R_{0,2}} + {R_{2,0}} + {R_{1,1}} + \widehat x \circ {R_{3,3}} $ $ \widehat {{c_3}}(x) = {R_{0,3}} + {R_{3,0}} + {R_{1,2}} + {R_{2,1}} $ 7. for l=0; l<9; l++ for k=0; k<4; k++ $ c(x) = {\text{NTT(}}\hat c[l][0 - 63][k]{\text{)}} $ end for end for 8. for j=0; j<64; j++ for k=0; k<4; k++ $ c(x) = {\text{NTT(}}\hat c[0 - 8][j][k]{\text{)}} $ end for end for 算法2 基2-NTT算法的核心运算 $\hat a[k] = {{A} }[k] + {\zeta ^{2k + 1} }{{B} }[k]$ $\hat a\left[ {k + \dfrac{n}{2} } \right] = {{A} }[k] - {\zeta ^{2k + 1} }{{B} }[k]$ 算法3 基3-NTT算法的核心运算,其中$ \mu = {\omega ^{{n {\left/ {\vphantom {n 3}} \right. } 3}}} $ $\hat a[k] = {{A} }[k] + {\omega ^k}{{B} }[k] + {\left( { {\omega ^k} } \right)^2}{ {C} }[k]$ $\begin{aligned} \hat a\left[ {k + \frac{n}{3} } \right] = & {{A} }[k] + \mu {\omega ^k}{B}[k] + {\mu ^2}{\left( { {\omega ^k} } \right)^2}{ {C} }[k] \\ \;\;\;\;\;\;\;\;\;\;\; =& { {A} }[k] - {\left( { {\omega ^k} } \right)^2}{C}[k] + \mu \left( { {\omega ^k}{B}[k] - { {\left( { {\omega ^k} } \right)}^2}{C}[k]} \right) \end{aligned}$ $ \begin{aligned} \hat a\left[ {k + \frac{{2n}}{3}} \right] =& {A}[k] + {\mu ^2}{\omega ^k}{B}[k] + \mu {\left( {{\omega ^k}} \right)^2}{C}[k] \\ \;\;\;\;\;\;\;\;\;\;\;\; =& {A}[k] - {\omega ^k}{B}[k] - \mu \left( {{\omega ^1}{B}[k] - {{\left( {{\omega ^k}} \right)}^2}{C}[k]} \right) \\ \end{aligned} $ 算法4 基4-NTT算法的核心运算,其中$ \mu = {\omega ^{{n \mathord{\left/ {\vphantom {n 4}} \right. } 4}}} $ $\hat a[k] = {A}[k] + {\zeta ^{2k + 1}}{B}[k] + {\left( {{\zeta ^{2k + 1}}} \right)^2}{C}[k] + {\left( {{\zeta ^{2k + 1}}} \right)^3}{D}[k] $ $ \begin{aligned} \hat a\left[ {k + \frac{n}{4}} \right] =& {A}[k] + {\mu ^2}{\zeta ^{2k + 1}}{B}[k] + {\left( {{\mu ^2}{\zeta ^{2k + 1}}} \right)^2}{C}[k] + {\left( {{\mu ^2}{\zeta ^{2k + 1}}} \right)^3}{D}[k] \\ = &{A}[k] - {\zeta ^{2k + 1}}{B}[k] + {\left( {{\zeta ^{2k + 1}}} \right)^2}{C}[k] - {\left( {{\zeta ^{2k + 1}}} \right)^3}{D}[k] \end{aligned} $ $ \begin{aligned} \hat a\left[ {k + \frac{n}{2}} \right] = &{A}[k] + \mu {\zeta ^{2k + 1}}{B}[k] + {\left( {\mu {\zeta ^{2k + 1}}} \right)^2}{C}[k] + {\left( {\mu {\zeta ^{2k + 1}}} \right)^3}{D}[k] \\ =& {A}[k] + \mu {\zeta ^{2k + 1}}{B}[k] - {\left( {{\zeta ^{2k + 1}}} \right)^2}{C}[k] - \mu {\left( {{\zeta ^{2k + 1}}} \right)^3}{D}[k] \\ \end{aligned} $ $\begin{aligned} \hat a\left[ {k + \frac{{3n}}{4}} \right] =& {A}[k] + {\mu ^3}{\zeta ^{2k + 1}}{B}[k] + {\left( {{\mu ^3}{\zeta ^{2k + 1}}} \right)^2}{C}[k] + {\left( {{\mu ^3}{\zeta ^{2k + 1}}} \right)^3}{D}[k] \\ = & {A}[k] - \mu {\zeta ^{2k + 1}}{B}[k] - {\left( {{\zeta ^{2k + 1}}} \right)^2}{C}[k] + \mu {\left( {{\zeta ^{2k + 1}}} \right)^3}{D}[k] \end{aligned} $ 算法5 基4-NTT算法的核心运算操作拆解,其中$ \mu = {\omega ^{{n \mathord{\left/ {\vphantom {n 4}} \right. } 4}}} $ 1. ${T_0} = {{A[} }k{\text{]} } + {\left( { {\zeta ^{2k + 1} } } \right)^2}{C[}k{\text{]} }$ ${ {T}_1} = {{A[} }k{\text{]} } - {\left( { {\zeta ^{2k + 1} } } \right)^2}{C[}k{\text{]} }$ ${ {T}_2} = {\zeta ^{2k + 1} }{{B[} }k{\text{]} } + {\left( { {\zeta ^{2k + 1} } } \right)^3}{D[}k{\text{]} }$ ${ {T}_3} = {\zeta ^{2k + 1} }{{B[} }k{\text{]} } - {\left( { {\zeta ^{2k + 1} } } \right)^3}{D[}k{\text{]} }$ 2. $ \hat a[k] = {{T}_0} + {{T}_2} $ $ \hat a[k + {n \mathord{\left/ {\vphantom {n 4}} \right. } 4}] = {{T}_0} - {{T}_2} $ $ \hat a[k + {n \mathord{\left/ {\vphantom {n 2}} \right. } 2}] = {{T}_1} + {{T}_3} \cdot \mu $ $ \hat a[k + {{3n} \mathord{\left/ {\vphantom {{3n} 4}} \right. } 4}] = {{T}_1} - {{T}_3} \cdot \mu $ 算法6 基3-NTT算法的核心运算操作拆解,其中$ \mu = {\omega ^{n/3}} $ 1. $ {T_0} = {\omega ^k}B{\text{[}}k{\text{]}} + {\left( {{\omega ^k}} \right)^2}{C[}k{\text{]}} $ $ {T_1} = {\omega ^k}B{\text{[}}k{\text{]}} - {\left( {{\omega ^k}} \right)^2}{C[}k{\text{]}} $ 2. $ {T}_{2}={\omega }^{k}B\text{[}k{{](T}}_{0}的中间结果\text{)}+{{T}}_{1}\cdot \mu $ $ {T}_{3}={\left({\omega }^{k}\right)}^{2}C\text{[}k{{](T}}_{0}的中间结果\text{)}-{{T}}_{1}\cdot \mu $ 3. $ \hat a[k] = {{A}}[k] + {{{T}}_0} $ $ \hat a[k + {n \mathord{\left/ {\vphantom {n 3}} \right. } 3}] = {{A}}[k] - {{{T}}_3} $ $ \hat a[k + {{2n} \mathord{\left/ {\vphantom {{2n} 3}} \right. } 3}] = {{A}}[k] - {{{T}}_2} $ 算法7 4路PtNTT中的点乘算法 1. for i=0; i<4; i++ for j=0; j<4; j++ $ {R_{i,j}} = \widehat {{a_i}}{\text{(}}x{\text{)}} \circ \widehat {{b_j}}{\text{(}}x{\text{)}} $ end for end for 2.$ \widehat {{c_0}}(x) = {R_{0,0}} + \widehat x \circ \left( {{R_{1,3}} + {R_{3,1}} + {R_{2,2}}} \right) $ $ \widehat {{c_1}}(x) = {R_{0,1}} + {R_{1,0}} + \widehat x \circ \left( {{R_{2,3}} + {R_{3,2}}} \right) $ $ \widehat {{c_2}}(x) = {R_{0,2}} + {R_{2,0}} + {R_{1,1}} + \widehat x \circ {R_{3,3}} $ $ \widehat {{c_3}}(x) = {R_{0,3}} + {R_{3,0}} + {R_{1,2}} + {R_{2,1}} $ 算法8 3路PtNTT中的点乘算法 1. for i=0; i<3; i++ for j=0; j<3; j++ $ {R_{i,j}} = \widehat {{a_i}}{\text{(}}x{\text{)}} \circ \widehat {{b_j}}{\text{(}}x{\text{)}} $ end for end for 2. $ \widehat {{c_0}}(x) = {R_{0,0}} + \widehat x \circ \left( {{R_{1,2}} + {R_{2,1}}} \right) $ $ \widehat {{c_1}}(x) = {R_{0,1}} + {R_{1,0}} + \widehat x \circ {R_{2,2}} $ $ \widehat {{c_2}}(x) = {R_{0,2}} + {R_{2,0}} + {R_{1,1}} $ 算法9 16 bit模乘、32 bit乘法 输入:32 bit数据[A1,A0],32 bit数据[B1,B0],16 bit模数q,选
择数据sel(sel=0代表32比特相乘,sel=1代表16 bit模乘)预计算:m=$ \left\lfloor {{{{2^k}} \mathord{\left/ {\vphantom {{{2^k}} q}} \right. } q}} \right\rfloor $ 输 出:32 bit数据z 1. ${ {{M} }_1} = {{A} }_0 \times {{B_0} }$ 2. if(sel) ${ {{M} }_2} = { {{M} }_1}[15:0] \times m$,${ {{M} }_3} = { {{M} }_1}[31:16] \times m$ else ${ {{M} }_2} = {{A_1} } \times {{B_0} }$,${ {{M} }_3} = {{A} }0 \times {{B1} }$ 3. if(sel) ${ {{M} }_4} = \left( { { {{M} }_3} < < 16 + { {{M} }_2} } \right)[47:32] \times q$ else ${ {{M} }_4} = {{A_1} } \times {{B_1} }$ 4. if(sel) ${\text{addsub} }_{1}={{M} }_{1}-{{M} }_{3}$ else ${\text{addsu} }{ {\text{b} }_1} = { {{M} }_2} + { {{M} }_3}$ 5. if(sel) $ {\text{addsu}}{{\text{b}}_2} = {\text{addsu}}{{\text{b}}_1} - q $ else ${\text{addsu} }{ {\text{b} }_2} = \left( { {\text{addsu} }{ {\text{b} }_1} < < 16} \right) + { {{M} }_1}$ 6. if(sel) $ z = \left( {{\text{addsu}}{{\text{b}}_2} < 0} \right)?{\text{addsu}}{{\text{b}}_1}:{\text{addsu}}{{\text{b}}_2} $ else $z = \left( { { {{M} }_4} < < 32} \right) + {\text{addsu} }{ {\text{b} }_2}$ 表 2 基于FPGA不同多项式乘法架构性能对比
文献 年份 频率/
MHz时钟
周期数时延
/μs工艺 参数 资源
(LUT/FF/
BRAM/DSP)时延性
能对比支持
算法[7] 2020 – 3865 – Zynq-7000 n=256, q=3329 2908/-/-/9 – Kyber 226081 n=256, q=213 Saber [8] 2022 250 932 3.728 UltraScale+ n=256, q=3329 – 2.33 Kyber 1024 4.096 n=256, q=213 2.56 Saber [6] 2022 232 1627 7.013 Artix-7 n=256, q<232 6976/-/24/16 – q≡1mod2n
条件下2798 12.060 n=512, q<232 1.19 5251 22.634 n=1024, q<232 – 10455 45.065 n=2048, q<232 – [9] 2022 – 224 – Artix-7 n=256, q=3329 25674/3137/6/64 – Kyber n=256, q=8380417 Dilithium [14] 2022 265 246 0.928 Artix-7 n=256, q=3329 9211/9810/1/60 0.58 Kyber 261
257454
8461.740
3.292Spartan-7
Artix-7n=512, q=12289
n=1024,q=1228922800/45600
/1/68
23261/14901
/1/76–
–NewHope 本文 – 152 243 1.599 Artix-7 n=256, q=3329 13794/-/3×36K/48 1 Kyber 896 5.895 n=256, q=8380417 Dilithium 243 1.599 n=256, q=213 Saber 3794
3770
611224.961
24.803
40.211n=701, q=8192
n=677, q=2048
n=821, q=4096NTRU -
[1] SHOR P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. SIAM Review, 1999, 41(2): 303–332. doi: 10.1137/S0036144598347011 [2] ALAGIC G, ALPERIN-SHERIFF J, APON D, et al. Status report on the second round of the NIST post-quantum cryptography standardization process[R]. NIST IR 8309, 2020. [3] ALAGIC G, ALPERIN-SHERIFF J, APON D, et al. Status report on the first round of the NIST post-quantum cryptography standardization process[R]. NISTIR 8240, 2019. [4] BANERJEE U, UKYAB T S, and CHANDRAKASAN A P. Sapphire: A configurable crypto-processor for post-quantum lattice-based protocols[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2019, 2019(4): 17–61. doi: 10.13154/tches.v2019.i4.17-61 [5] FRITZMANN T, SHARIF U, MÜLLER-GRITSCHNEDER D, et al. Towards reliable and secure post-quantum co-processors based on RISC-V[C]. 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 2019: 1148–1153. [6] 刘冬生, 赵文定, 刘子龙, 等. 应用于格密码的可重构多通道数论变换硬件设计[J]. 电子与信息学报, 2022, 44(2): 566–572. doi: 10.11999/JEIT210114LIU Dongsheng, ZHAO Wending, LIU Zilong, et al. Reconfigurable hardware design of multi-lanes number theoretic transform for lattice-based cryptography[J]. Journal of Electronics &Information Technology, 2022, 44(2): 566–572. doi: 10.11999/JEIT210114 [7] FRITZMANN T, SIGL G, and SEPÚLVEDA J. RISQ-V: Tightly coupled RISC-V accelerators for post-quantum cryptography[R]. Paper 2020/446, 2020. [8] LI Aobo, LIU Dongsheng, LI Xiang, et al. A flexible instruction-based post-quantum cryptographic processor with modulus reconfigurable arithmetic unit for module LWR&E[C]. 2022 IEEE Asian Solid-State Circuits Conference (A-SSCC), Taipei, China, 2022: 1–3. [9] ZHAO Yifan, XIE Ruiqi, XIN Guozhu, et al. A high-performance domain-specific processor with matrix extension of RISC-V for module-LWE Applications[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2022, 69(7): 2871–2884. doi: 10.1109/TCSI.2022.3162593 [10] ZHU Yihong, ZHU Wenping, ZHU Min, et al. A 28nm 48KOPS 3.4µJ/Op agile crypto-processor for post-quantum cryptography on multi-mathematical problems[C]. 2022 IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, USA, 2022: 514–516. [11] ALKIM E, CHENG D Y L, CHUNG C M M, et al. Polynomial multiplication in NTRU Prime: Comparison of optimization strategies on Cortex-M4[R]. Paper 2020/1216, 2020. [12] 曲英杰. 可重构密码协处理器的组成与结构[J]. 计算机工程与应用, 2003, 39(23): 32–34. doi: 10.3321/j.issn:1002-8331.2003.23.011QU Yingjie. Components and structure of reconfigurable cipher coprocessor[J]. Computer Engineering and Applications, 2003, 39(23): 32–34. doi: 10.3321/j.issn:1002-8331.2003.23.011 [13] AIKATA A, MERT A C, JACQUEMIN D, et al. A unified cryptoprocessor for lattice-based signature and key-exchange[J]. IEEE Transactions on Computers, 2023, 72(6): 1568–1580. doi: 10.1109/TC.2022.3215064 [14] DUONG-NGOC P and LEE H. Configurable mixed-radix number theoretic transform architecture for lattice-based cryptography[J]. IEEE Access, 2022, 10: 12732–12741. doi: 10.1109/ACCESS.2022.3145988 -





 下载:
下载:

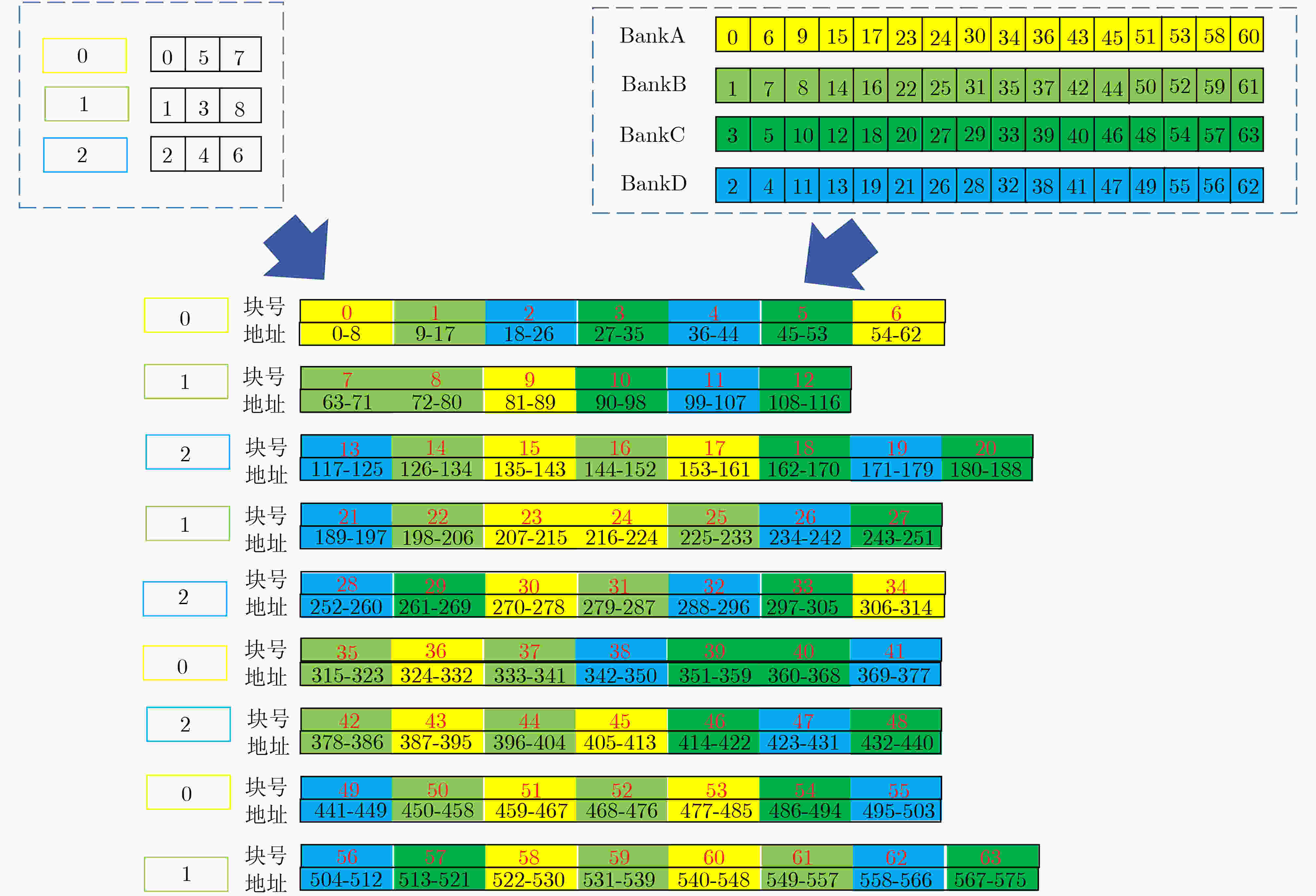
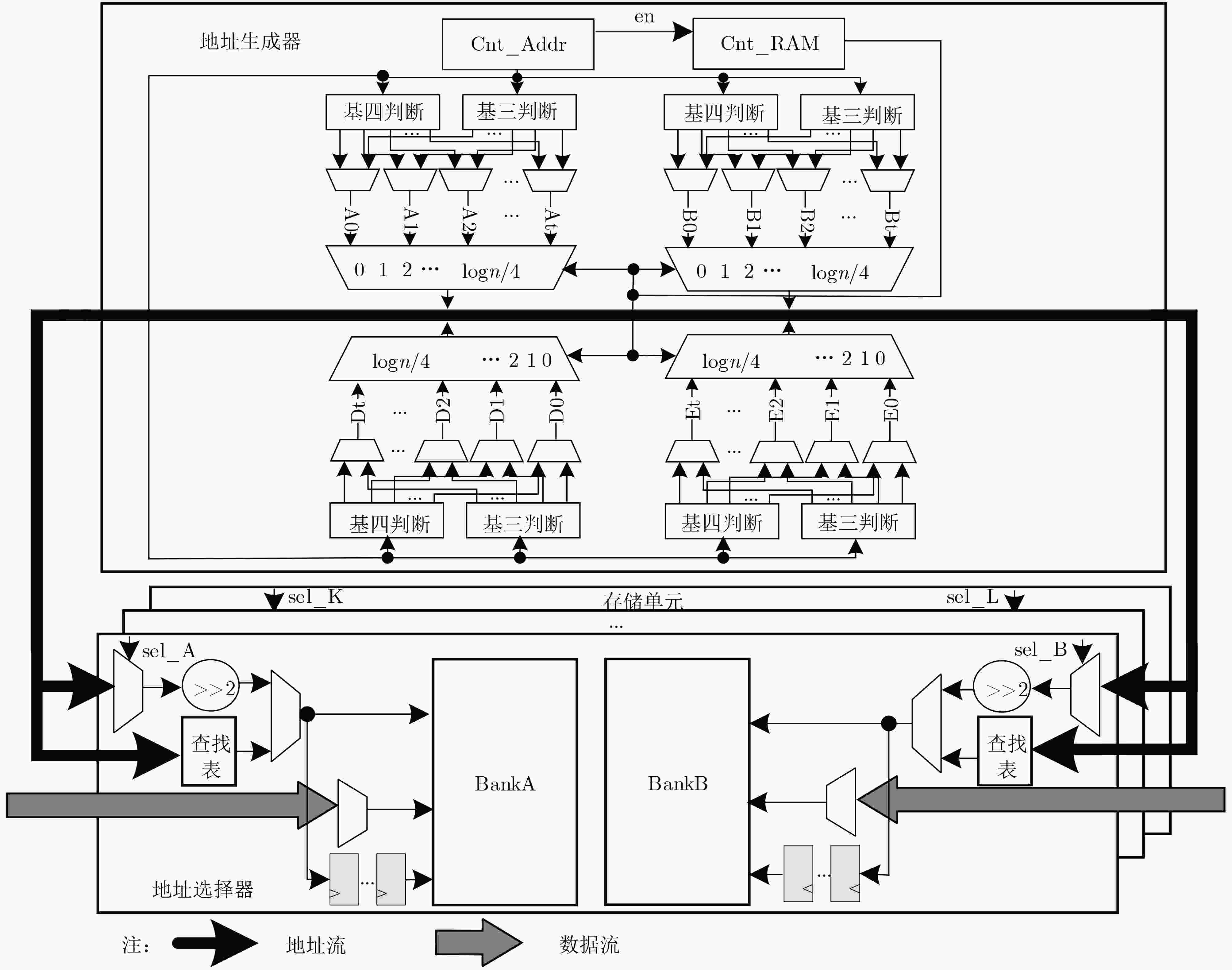


 下载:
下载:
