Research on Low Complexity Underwater Acoustic Multiple Input Multiple Output Orthogonal Time Frequency Space Modulation Communication Method
-
摘要: 在多输入多输出正交时频空调制(MIMO-OTFS)水声通信系统中,基于消息传递(MP)算法的MIMO-OTFS通信的计算复杂度较高,在实际应用中会增加设备成本。针对上述问题,该文提出一种基于2维虚拟时间反转镜(VTRM)的MIMO-OTFS均衡算法,该算法利用VTRM的时频空聚焦特性,有效提高了均衡性能,并通过改进的2维比例归一化最小均方(IPNLMS)算法进行信道估计,该算法利用时延-多普勒域信道的稀疏特性以较低的复杂度提高了收敛速度,最后通过2维自适应判决反馈均衡算法消除残余的码间串扰,进一步提高系统性能。仿真结果表明,所提均衡算法具有可行性,且在保证相同性能时,复杂度低于MP算法。Abstract: In the Multiple Input Multiple Output Orthogonal Time Frequency Space (MIMO-OTFS) underwater acoustic communication system, MIMO-OTFS communication based on the Message Passing (MP) algorithm have problems with high computational complexity, which may increase equipment costs in practical applications. To solve this problem, an MIMO-OTFS equalization algorithm based on two-dimensional Virtual Time Reversal Mirror (VTRM) is proposed, which uses the time-frequency-space focusing characteristics of VTRM to effectively improve the equalization performance. The channel estimation is performed using the Improved two-dimensional Proportional Normalized Least Mean Square (IPNLMS) algorithm, which utilizes the sparse characteristics of the time-delay Doppler domain channel to improve convergence speed at a lower computational complexity. Finally, residual inter-symbol interference is eliminated and system performance is further improved through the use of the two-dimensional adaptive decision feedback equalization algorithm. The simulation results demonstrate the feasibility of the proposed equalization algorithm, and show that it has lower complexity than the MP algorithm while ensuring the same performance.
-
表 1 仿真参数
仿真参数 符号 值 发射阵元数 $ {N_{\text{t}}} $ 2 接收阵元数 $ {N_{\text{r}}} $ 6 子载波数 M 512 符号数 N 128 最低子载波频率 $ {f_0} $ 12 kHz 信号带宽 B 4 kHz 子载波间隔 $ \Delta f $ 7.81 Hz OTFS符号周期 $ {T_{\text{s}}} $ 0.25 ms 循环前缀时长 ${T_{ \rm{CP} } }$ 32 ms OTFS帧时长 ${T_{ \rm{OTFS} } }$ 20.48 s -
[1] STOJANOVIC M and PREISIG J. Underwater acoustic communication channels: Propagation models and statistical characterization[J]. IEEE Communications Magazine, 2009, 47(1): 84–89. doi: 10.1109/MCOM.2009.4752682 [2] AVRASHI G, AMAR A, and COHEN I. Time-varying carrier frequency offset estimation in OFDM underwater acoustic communication[J]. Signal Processing, 2022, 190: 108299. doi: 10.1016/j.sigpro.2021.108299 [3] JIA Shuyang, ZOU Sichen, ZHANG Xiaochuan, et al. Multi-block Sparse Bayesian learning channel estimation for OFDM underwater acoustic communication based on fractional Fourier transform[J]. Applied Acoustics, 2022, 192: 108721. doi: 10.1016/j.apacoust.2022.108721 [4] ZHANG Yonglin, LI Chao, WANG Haibin, et al. Deep learning aided OFDM receiver for underwater acoustic communications[J]. Applied Acoustics, 2022, 187: 108515. doi: 10.1016/j.apacoust.2021.108515 [5] WANG Zhizhan, LI Yuzhou, WANG Chengcai, et al. A-OMP: An adaptive OMP algorithm for underwater acoustic OFDM channel estimation[J]. IEEE Wireless Communications Letters, 2021, 10(8): 1761–1765. doi: 10.1109/LWC.2021.3079225 [6] 朱雨男, 解方彤, 张明亮, 等. 基于多层双向长短时记忆网络的水声多载波通信索引检测方法[J]. 电子与信息学报, 2022, 44(6): 1984–1990. doi: 10.11999/JEIT210949ZHU Yunan, XIE Fangtong, ZHANG Mingliang, et al. Index detection for underwater acoustic multi-carrier communication based on deep bidirectional long short-term memory network[J]. Journal of Electronics &Information Technology, 2022, 44(6): 1984–1990. doi: 10.11999/JEIT210949 [7] WANG Tiejun, PROAKIS J G, MASRY E, et al. Performance degradation of OFDM systems due to Doppler spreading[J]. IEEE Transactions on Wireless Communications, 2006, 5(6): 1422–1432. doi: 10.1109/TWC.2006.1638663 [8] HADANI R, RAKIB S, TSATSANIS M, et al. Orthogonal time frequency space modulation[C]. 2017 IEEE Wireless Communications and Networking Conference, San Francisco, USA, 2017: 1–6. [9] REZAZADEHREYHANI A, FARHANG A, JI Mingyue, et al. Analysis of discrete-time MIMO OFDM-based orthogonal time frequency space modulation[C]. 2018 IEEE International Conference on Communications, Kansas City, USA, 2018: 1–6. [10] LI Shuangyang, YUAN Jinhong, YUAN Weijie, et al. Performance analysis of coded OTFS systems over high-mobility channels[J]. IEEE Transactions on Wireless Communications, 2021, 20(9): 6033–6048. doi: 10.1109/TWC.2021.3071493 [11] WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Orthogonal time-frequency space modulation: A promising next-generation waveform[J]. IEEE Wireless Communications, 2021, 28(4): 136–144. doi: 10.1109/MWC.001.2000408 [12] WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Transmitter and receiver window designs for orthogonal time-frequency space modulation[J]. IEEE Transactions on Communications, 2021, 69(4): 2207–2223. doi: 10.1109/TCOMM.2021.3051386 [13] RAVITEJA P, PHAN K T, HONG Yi, et al. Interference cancellation and iterative detection for orthogonal time frequency space modulation[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6501–6515. doi: 10.1109/TWC.2018.2860011 [14] MURALI K R and CHOCKALINGAM A. On OTFS modulation for high-Doppler fading channels[C]. 2018 Information Theory and Applications Workshop, San Diego, USA, 2018: 1–10. [15] JING Lianyou, ZHANG Namin, HE Chengbing, et al. OTFS underwater acoustic communications based on passive time reversal[J]. Applied Acoustics, 2022, 185: 108386. doi: 10.1016/j.apacoust.2021.108386 [16] RAMACHANDRAN M K and CHOCKALINGAM A. MIMO-OTFS in high-Doppler fading channels: Signal detection and channel estimation[C]. 2018 IEEE Global Communications Conference, Abu Dhabi, United Arab Emirates, 2018: 206–212. [17] SURABHI G D and CHOCKALINGAM A. Low-complexity linear equalization for 2×2 MIMO-OTFS signals[C]. 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications, Atlanta, USA, 2020: 1–5. [18] LI Muye, ZHANG Shun, GAO Feifei, et al. A new path division multiple access for the massive MIMO-OTFS networks[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(4): 903–918. doi: 10.1109/JSAC.2020.3018826 [19] BOCUS M J, DOUFEXI A, and AGRAFIOTIS D. Performance of OFDM‐based massive MIMO OTFS systems for underwater acoustic communication[J]. IET Communications, 2020, 14(4): 588–593. doi: 10.1049/iet-com.2019.0376 [20] HADHOUD M M and THOMAS D W. The two-dimensional adaptive LMS (TDLMS) algorithm[J]. IEEE Transactions on Circuits and Systems, 1988, 35(5): 485–494. doi: 10.1109/31.1775 [21] JING Lianyou, WANG Han, HE Chengbing, et al. Two dimensional adaptive multichannel decision feedback equalization for OTFS system[J]. IEEE Communications Letters, 2021, 25(3): 840–844. doi: 10.1109/LCOMM.2020.3039982 [22] QARABAQI P and STOJANOVIC M. Statistical characterization and computationally efficient modeling of a class of underwater acoustic communication channels[J]. IEEE Journal of Oceanic Engineering, 2013, 38(4): 701–717. doi: 10.1109/JOE.2013.2278787 [23] SHEN Wenqian, DAI Linglong, AN Jianping, et al. Channel estimation for orthogonal time frequency space (OTFS) massive MIMO[J]. IEEE Transactions on Signal Processing, 2019, 67(16): 4204–4217. doi: 10.1109/TSP.2019.2919411 [24] BENESTY J and GAY S L. An improved PNLMS algorithm[C]. Proceedings of 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, USA, 2002: II-1881–II-1884. -





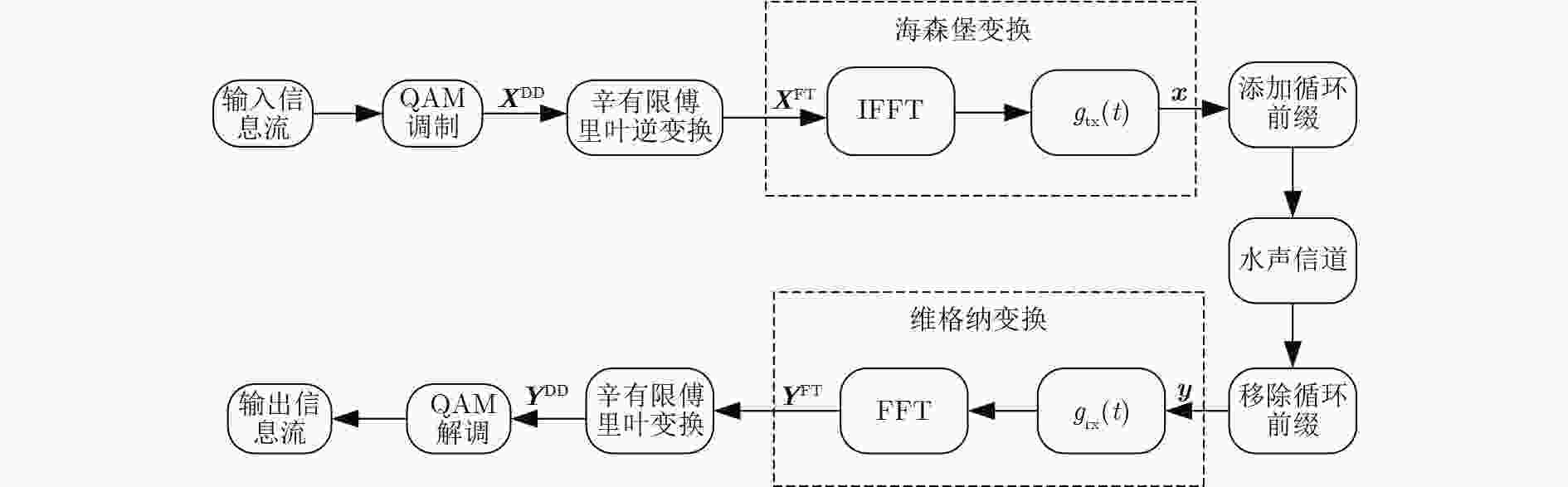
 下载:
下载:
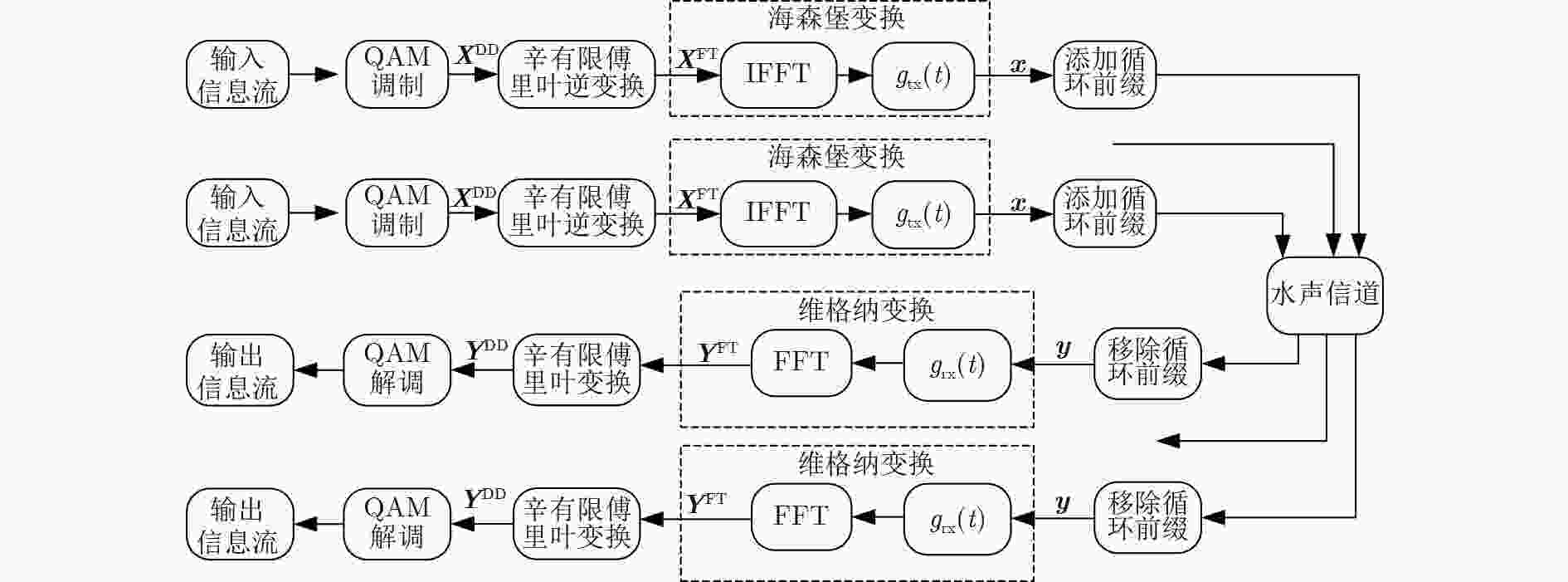
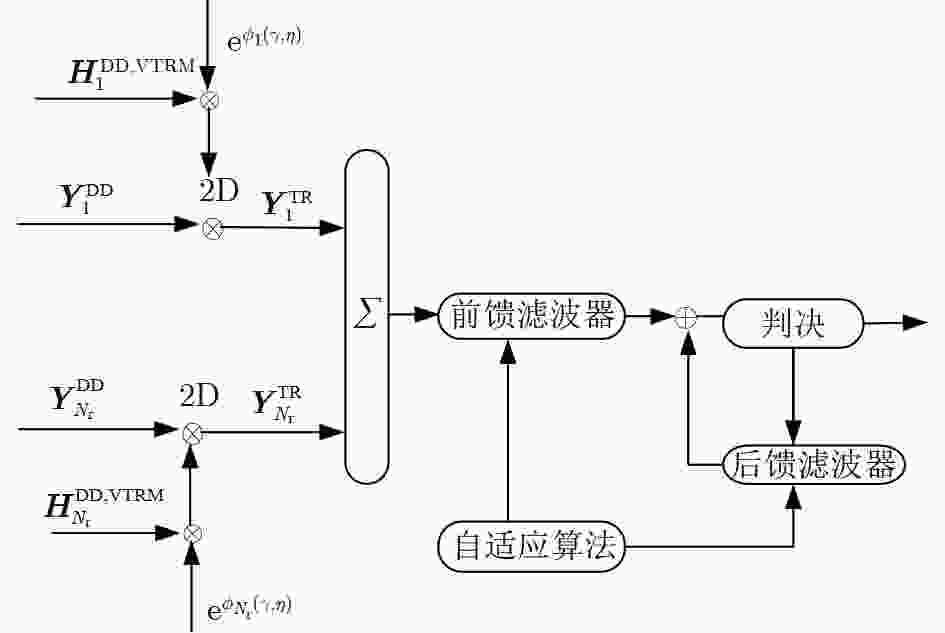
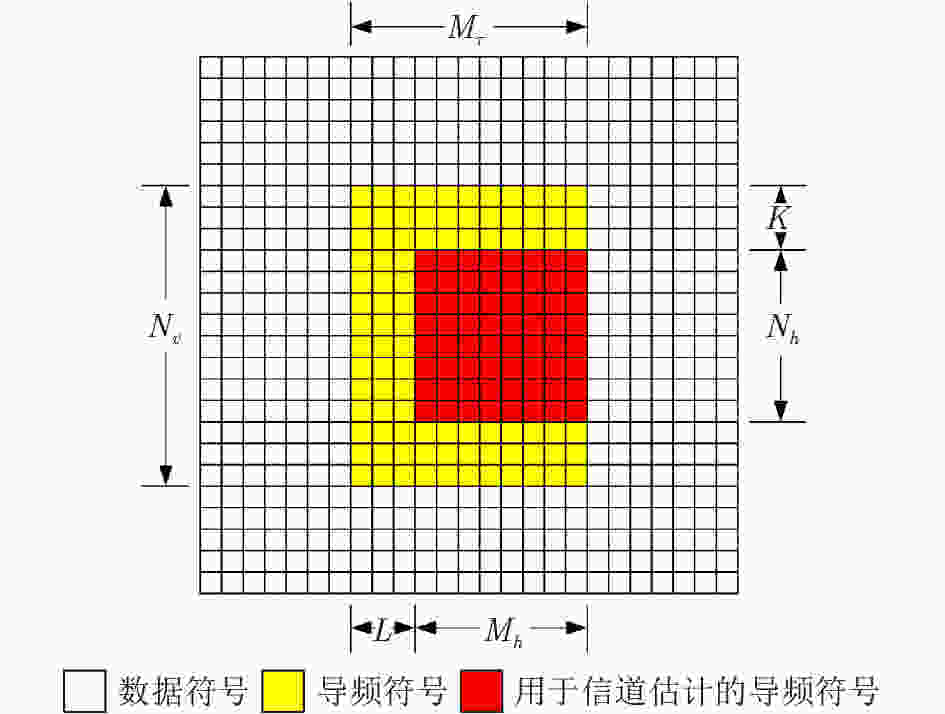


 下载:
下载:
