DOA Estimation of Direction Vector Estimation Algorithm Based on Second-order Statistical Properties
-
摘要: 为了减小天线阵流形误差对波达方向(DOA)估计结果的影响,以及克服基于传统盲源分离算法的DOA估计算法不能应用于少通道测向设备的不足,提出一种基于2阶统计特性的方向向量估计算法的DOA估计算法。首先,根据确定性最大似然(DML)估计算法谱函数的特征,构造关于协方差矩阵的酉约束下的优化问题;然后,通过优化该问题获得各个单信号的实际方向向量;最后,将各个单信号的实际方向向量输入到空间谱算法中实现DOA估计。由于将多信号的DOA估计转化为多个单信号的DOA估计,因此在天线阵列流形存在误差时,所提算法比传统的DOA方法具有更好的DOA估计性能。由于所提算法仅需使用协方差矩阵,因此所提算法可应用于少通道测向设备。由仿真实验结果可知,在阵列流形存在误差以及测向设备为少通道测向设备时,与传统DOA方法相比,所提算法的DOA估计的准确度、抗扰度以及分辨率更高。Abstract: In order to reduce the influence of errors of antenna array manifold on Direction of Arrival (DOA) estimation results, and to overcome the shortcoming of DOA estimation algorithm based on traditional blind source separation algorithm that can not be applied to direction-finding equipment with few channel receivers, a DOA estimation algorithm of direction vector estimation algorithm based on second-order statistical properties is proposed. Firstly, according to the characteristics of spectral function of Deterministic Maximum Likelihood (DML) estimation algorithm, an optimization problem with unitary constraints on covariance matrix is constructed. Then, the actual direction vector of each single signal is obtained by optimizing the problem. Finally, the actual direction vectors of each single signal are input into the spatial spectral algorithm to achieve DOA estimation. Because the DOA estimation of multiple signals is transformed into the DOA estimation of multiple single signals, the proposed algorithm has better DOA estimation performance than the traditional DOA method when the antenna array manifold has errors. Because the proposed algorithm only uses covariance matrix, the proposed algorithm can be applied to direction-finding equipment with few channel receivers. The simulation results show that the proposed algorithm has higher accuracy, immunity and resolution than the traditional DOA estimation algorithm when the array manifold has errors and the equipment is the direction-finding equipment with few channel receivers.
-
算法1 酉约束下的粒子群算法 (1) 设置粒子群算法迭代次数上限,初始化粒子群; (2) 根据使式(13)最小的原则,对粒子的速度和位置进行更新,
每次更新后用$\pi $变换将粒子的位置修正为酉矩阵;(3) 若达到迭代次数上限或种群中所有粒子的位置都接近粒子群
的历史最佳位置,则转至步骤4,否则,转至步骤2;(4) 粒子群的历史最佳位置即为所需酉矩阵U。 算法2 酉约束下的梯度下降算法 (1) 设置梯度下降算法迭代次数上限,随机初始化酉矩阵U,初
始化步长$ \gamma = 1 $;(2) 计算损失函数$J({\boldsymbol{U}})$的1阶导矩阵${{\boldsymbol{D}}_x}$; (3) 计算负梯度Z; (4) 计算$\left\langle { {\boldsymbol{Z} },{\boldsymbol{Z} } } \right\rangle$,当$\left\langle { {\boldsymbol{Z} },{\boldsymbol{Z} }} \right\rangle$足够小或达到迭代次数上限
时,转到步骤8;(5) $J({\boldsymbol{U} }) - J(\pi ({\boldsymbol{U} } + 2\gamma {\boldsymbol{Z} })) \ge \gamma \left\langle { {\boldsymbol{Z} },{\boldsymbol{Z} }} \right\rangle$,则$ \gamma : = 2\gamma $,重复
步骤5,否则,执行步骤6;(6) $J({\boldsymbol{U} }) - J(\pi ({\boldsymbol{U} } + \gamma {\boldsymbol{Z} })) \prec (1/2)\gamma \left\langle { {\boldsymbol{Z} },{\boldsymbol{Z} } } \right\rangle$,则$\gamma : = (1/2)\gamma$,
重复步骤6,否则,执行步骤7;(7) 更新U,令${\boldsymbol{U}} = \pi ({\boldsymbol{U}} + \gamma {\boldsymbol{Z}})$,转到步骤2; (8) 当前状态酉矩阵U即为所需。 算法3 基于2阶统计特性盲源分离的DOA估计算法 (1) 求样本协方差矩阵$\hat {\boldsymbol{R}}$; (2) 使用MMDL算法计算独立信源个数N; (3) 初始化矩阵${{\boldsymbol{W}}_0}$。对$\hat {\boldsymbol{R}}$进行特征值分解,选取N个大特征值
所对应的特征向量构成${{\boldsymbol{W}}_0}$;(4) 使用算法1或算法2求得所需酉矩阵U; (5) 令${\boldsymbol{W}} = {{\boldsymbol{W}}_0}{\boldsymbol{U}}$,得到实际方向矩阵W; (6) 将W的每一列${{\boldsymbol{w}}_n}$输入到式(10)中得到DML伪谱,寻找峰
值得到波达方向的估计值。表 1 两种优化算法收敛速度对比
算法 平均收敛次数(次) 平均收敛时间(s) 酉约束下的粒子群算法 24 2.7238 酉约束下的梯度下降算法 52 1.0495 表 2 3种算法DOA估计结果
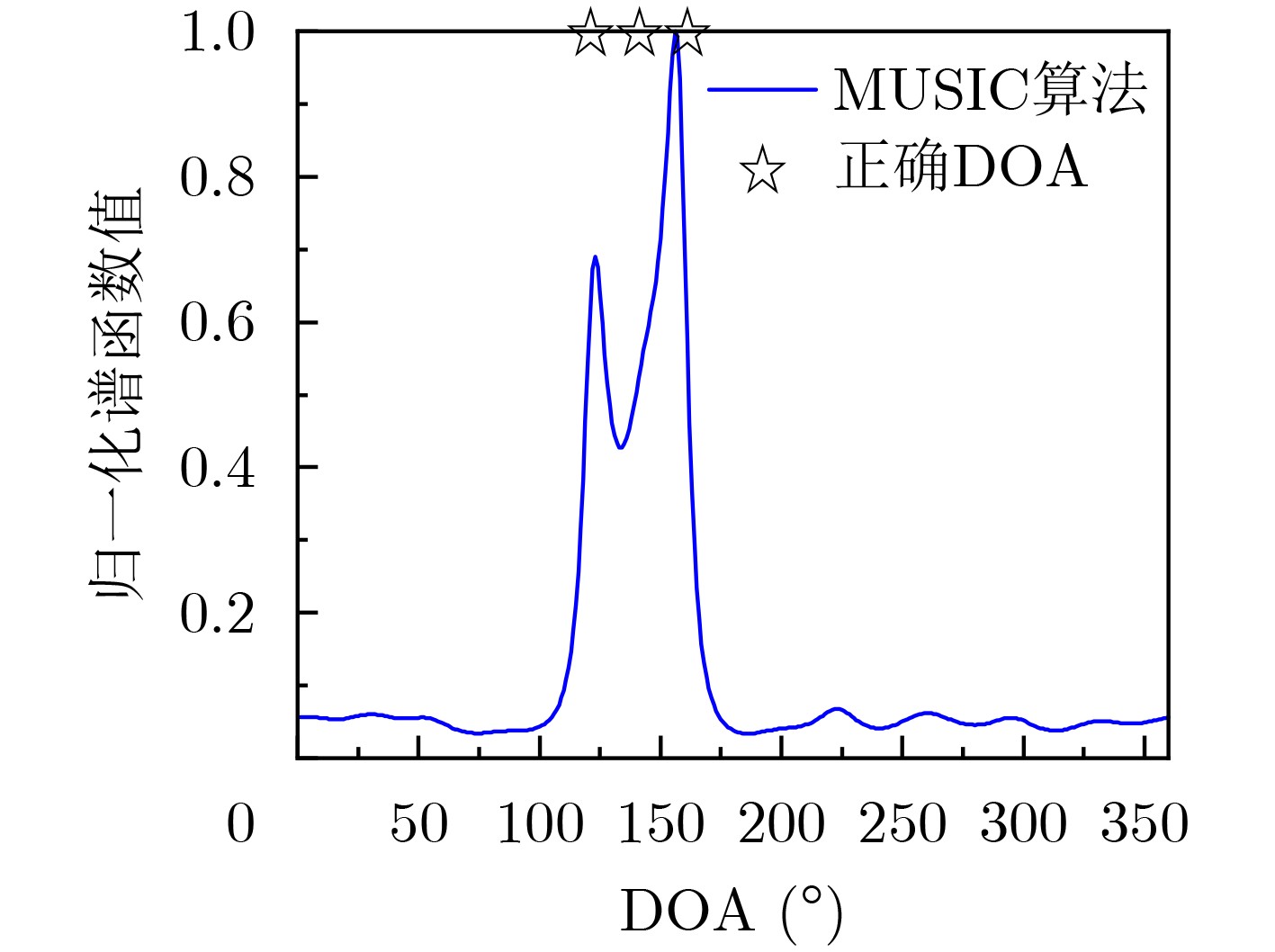
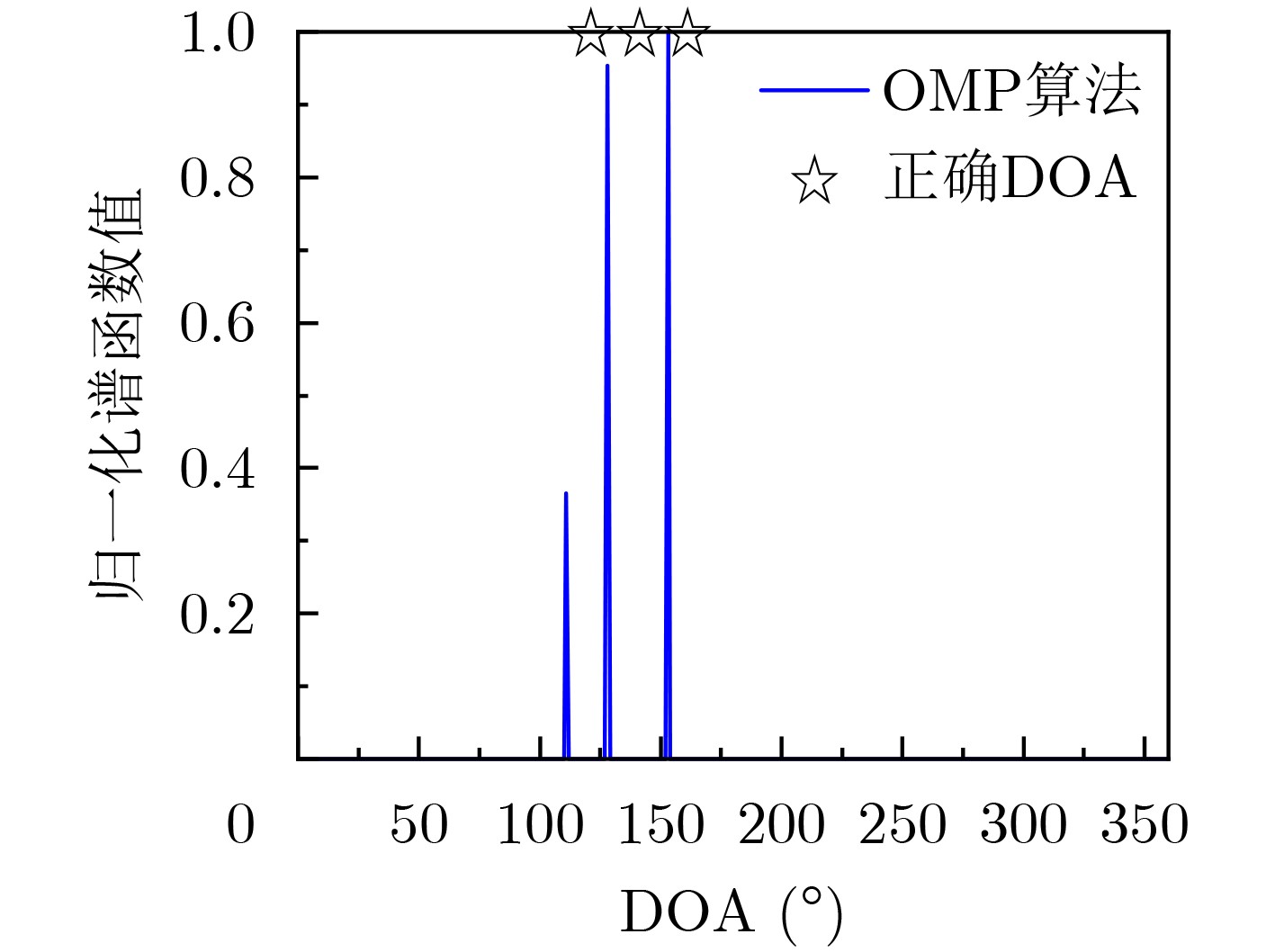
DOA算法 DOA估计结果 最大误差 正确DOA [120°], [140°], [160°] – MUSIC算法 [123°], [156°], [223°] 63 OMP算法 [111°], [128°], [153°] 12 本文算法 [118°], [143°], [164°] 4 -
[1] FUCHS J, KASPER A, LÜBKE M, et al. High-resolution direction-of-arrival estimation using distributed radar sensors[C]. 2022 IEEE Radio and Wireless Symposium (RWS), Las Vegas, USA, 2022: 53–56. [2] 王洪雁, 于若男, 潘勉, 等. 基于协方差矩阵重构的离网格DOA估计方法[J]. 电子与信息学报, 2021, 43(10): 2863–2870. doi: 10.11999/JEIT200697.WANG Hongyan, YU Ruonan, PAN Mian, et al. Off-grid DOA estimation method based on covariance matrix reconstruction[J]. Journal of Electronics &Information Technology, 2021, 43(10): 2863–2870. doi: 10.11999/JEIT200697. [3] WANG Lei, REN Chunhui, LIU Renting, et al. Direction-of-arrival estimation for nested array using mixed-resolution ADCs[J]. IEEE Communications Letters, 2022, 26(8): 1868–1872. doi: 10.1109/LCOMM.2022.3178617. [4] ZHAO Luming, LIU Hongqing, LI Yong, et al. DOA estimation under sensor gain and phase uncertainties[C]. 2015 International Conference on Estimation, Detection and Information Fusion (ICEDIF), Harbin, China, 2015: 209–213. [5] SCHENCK D, MESTRE X, and PESAVENTO M. Probability of resolution of MUSIC and g-MUSIC: An asymptotic approach[J]. IEEE Transactions on Signal Processing, 2022, 70: 3566–3581. doi: 10.1109/TSP.2022.3178820. [6] YANG Zai. Nonasymptotic performance analysis of ESPRIT and spatial-smoothing ESPRIT[J]. IEEE Transactions on Information Theory, 2023, 69(1): 666–681. doi: 10.1109/TIT.2022.3199405. [7] GONG Mingyan and LYU Bin. Alternating maximization and the EM algorithm in maximum-likelihood direction finding[J]. IEEE Transactions on Vehicular Technology, 2021, 70(10): 9634–9645. doi: 10.1109/TVT.2021.3106794. [8] WANG Wenyi and WU Renbiao. High resolution direction of arrival (DOA) estimation based on improved orthogonal matching pursuit (OMP) algorithm by iterative local searching[J]. Sensors, 2013, 13(9): 11167–11183. doi: 10.3390/s130911167. [9] WANG Qing, DOU Tongdong, CHEN Hua, et al. Effective block sparse representation algorithm for DOA estimation with unknown mutual coupling[J]. IEEE Communications Letters, 2017, 21(12): 2622–2625. doi: 10.1109/LCOMM.2017.2747547. [10] TIAN Ye, WANG Ran, CHEN Hua, et al. Real-valued DOA estimation utilizing enhanced covariance matrix with unknown mutual coupling[J]. IEEE Communications Letters, 2022, 26(4): 912–916. doi: 10.1109/LCOMM.2022.3148260. [11] LIU Jianfei, WU Xiongbin, EMERY W J, et al. Direction-of-arrival estimation and sensor array error calibration based on blind signal separation[J]. IEEE Signal Processing Letters, 2017, 24(1): 7–11. doi: 10.1109/LSP.2016.2632750. [12] 侯进, 李昀喆, 李天宇. 基于去噪复数FastICA和稀疏重构的相干信号欠定DOA估计[J]. 通信学报, 2021, 42(11): 172–181. doi: 10.11959/j.issn.1000-436x.2021219.HOU Jin, LI Yunzhe, and LI Tianyu. Underdetermined DOA estimation of coherent signals based on denoising complex FastICA and sparse reconstruction[J]. Journal on Communications, 2021, 42(11): 172–181. doi: 10.11959/j.issn.1000-436x.2021219. [13] BINGHAM E and HYVÄRINEN A. A fast fixed-point algorithm for independent component analysis of complex valued signals[J]. International Journal of Neural Systems, 2000, 10(1): 1–8. doi: 10.1142/S0129065700000028. [14] HU Jing and FAN Lehao. Application of JADE to separate complex-valued sources[C]. 2011 International Conference on Computer Science and Service System (CSSS), Nanjing, China, 2011: 1127–1129. [15] 赵自强, 曹岸杰, 杨勇, 等. 基于时间调制的单通道多基线相位干涉仪测向[J]. 电波科学学报, 2023, 38(1): 96–102,129. doi: 10.12265/j.cjors.2022096.ZHAO Ziqiang, CAO Anjie, YANG Yong, et al. Single-channel multiple baseline interferometer DF with time modulation[J]. Chinese Journal of Radio Science, 2023, 38(1): 96–102,129. doi: 10.12265/j.cjors.2022096. [16] BAZZI A, SLOCK D T M, and MEILHAC L. Detection of the number of superimposed signals using modified MDL criterion: A random matrix approach[C]. Proceedings of 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 2016: 4593–4597. [17] JIANG Jiajia, WEI Wenxue, SHAO Wanlu, et al. Research on large-scale Bi-level particle swarm optimization algorithm[J]. IEEE Access, 2021, 9: 56364–56375. doi: 10.1109/ACCESS.2021.3072199. [18] MANTON J H. Optimization algorithms exploiting unitary constraints[J]. IEEE Transactions on Signal Processing, 2002, 50(3): 635–650. doi: 10.1109/78.984753. [19] ABRUDAN T E, ERIKSSON J, and KOIVUNEN V. Steepest descent algorithms for optimization under unitary matrix constraint[J]. IEEE Transactions on Signal Processing, 2008, 56(3): 1134–1147. doi: 10.1109/TSP.2007.908999. [20] BIRTEA P, CAŞU I, and COMĂNESCU D. Constraint optimization and SU(N) quantum control landscapes[J]. Journal of Physics A:Mathematical and Theoretical, 2022, 55(11): 115301. doi: 10.1088/1751-8121/ac5189. -





 下载:
下载:



 下载:
下载:
