Time Domain Parallel Calculation Method for the Coupling of Transmission Line Network Terminated with Complex Circuits
-
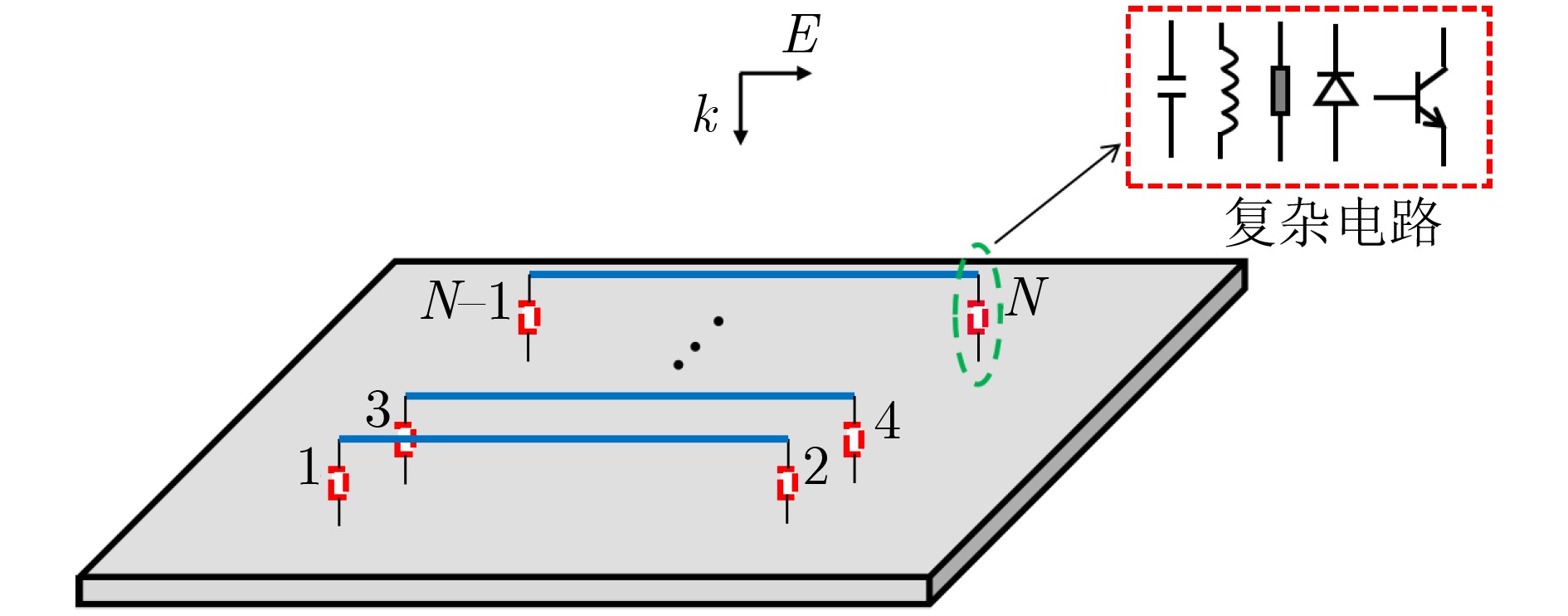
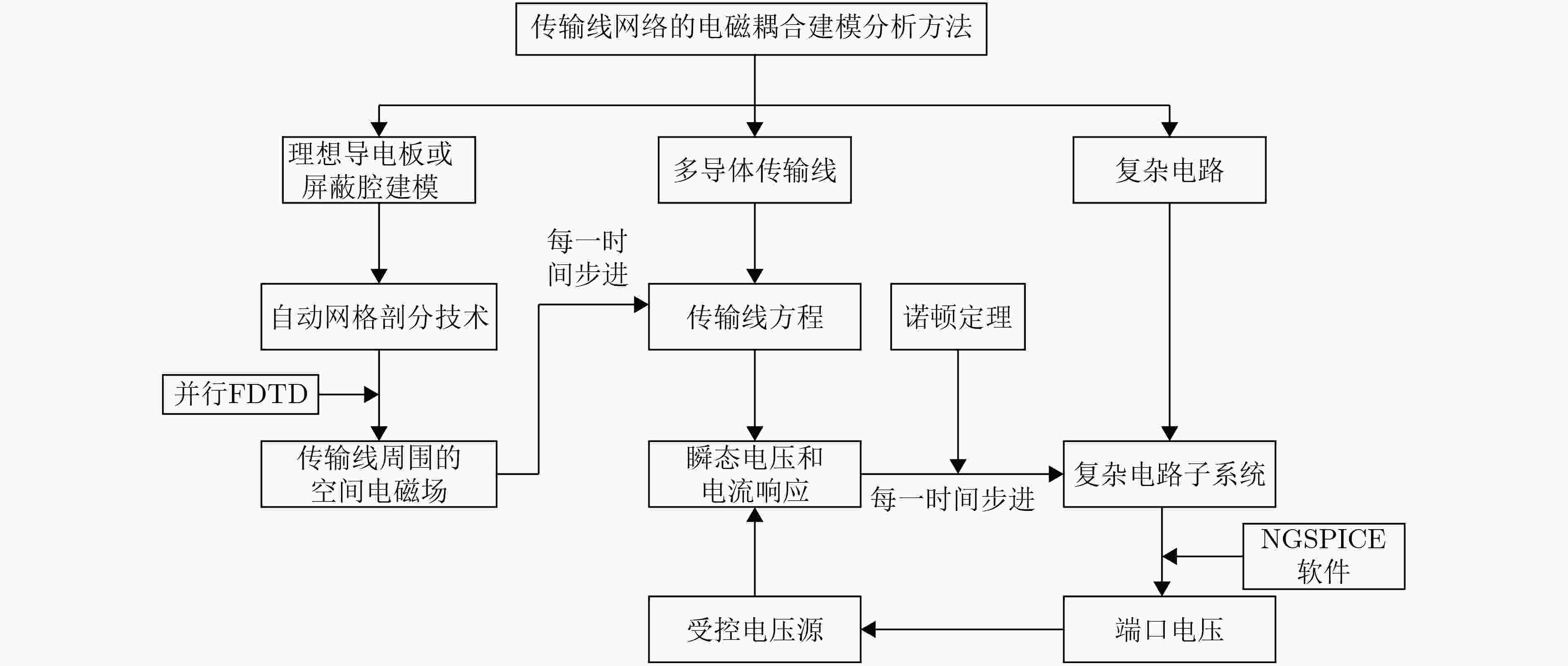
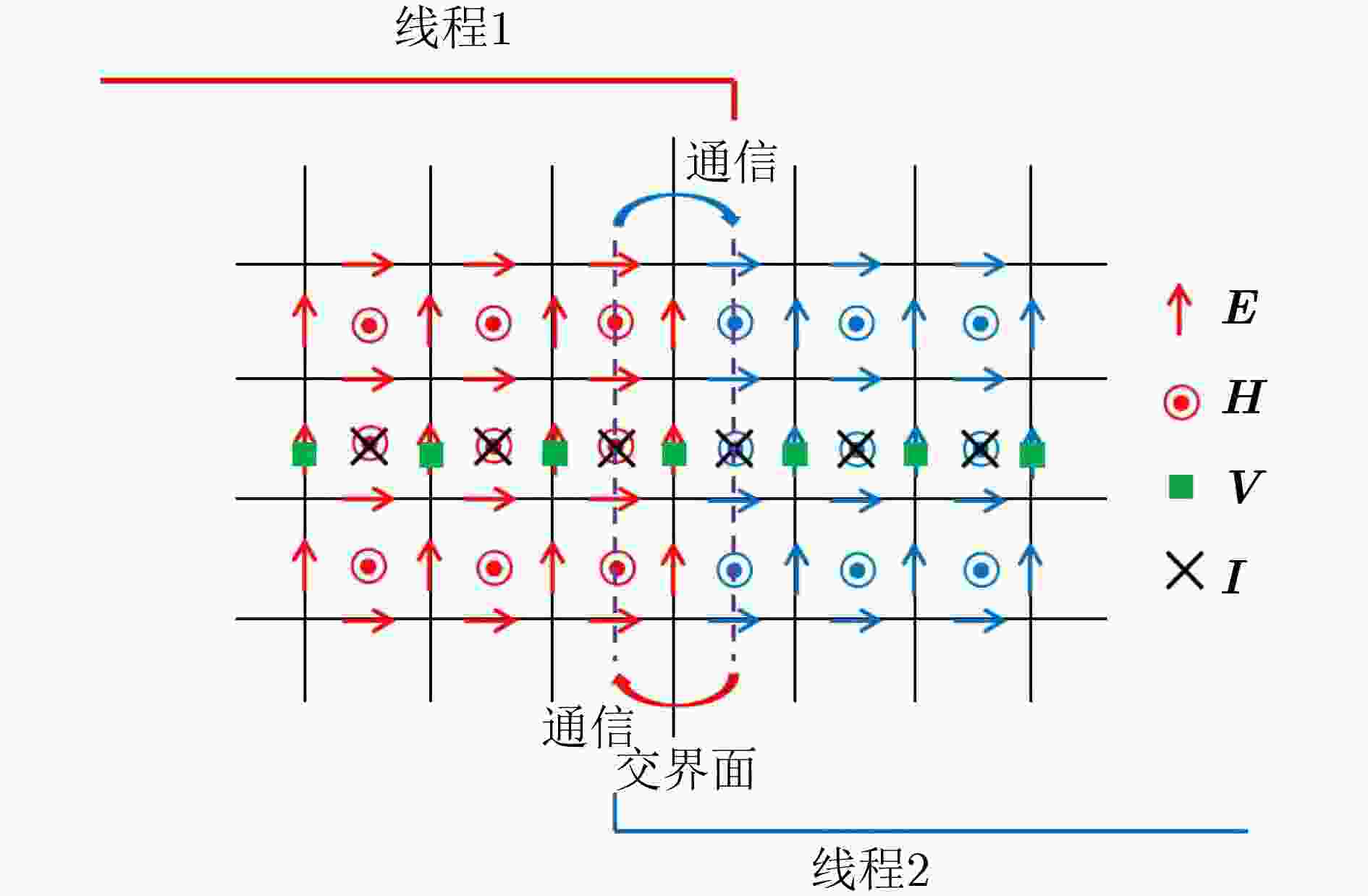
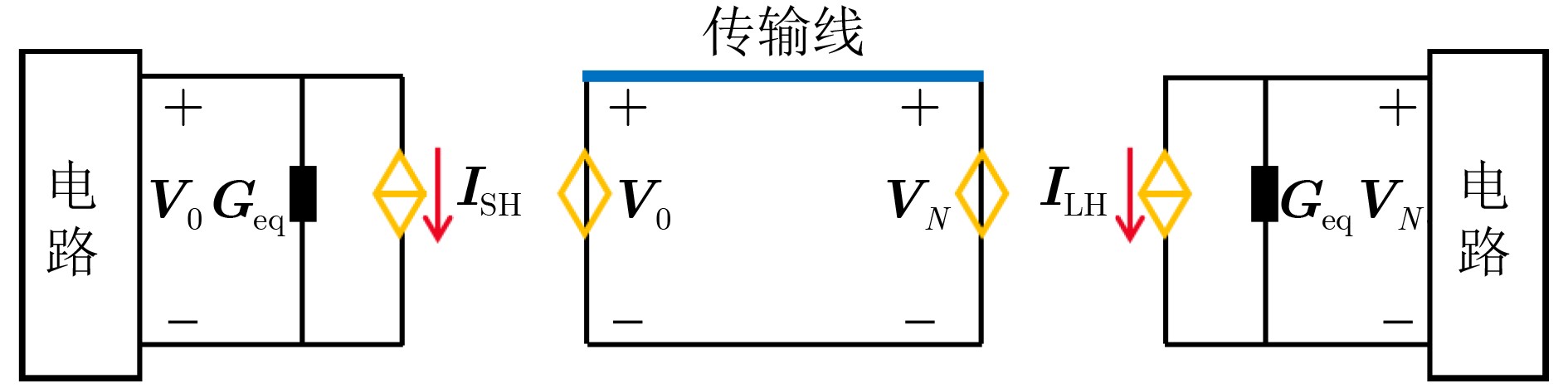
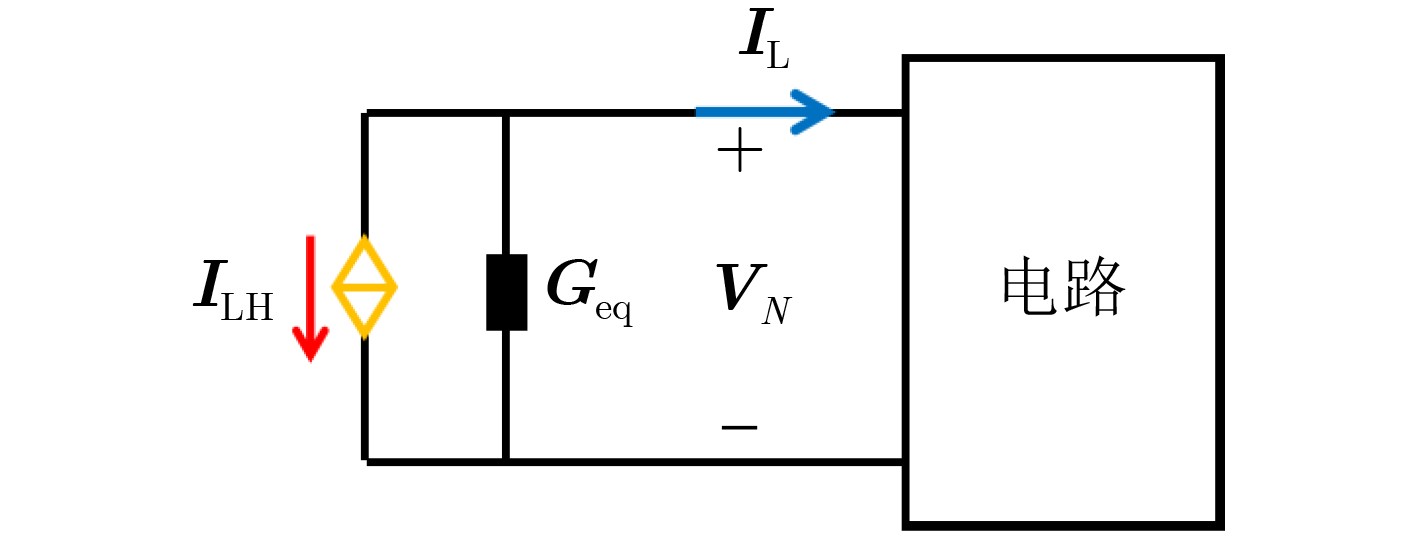
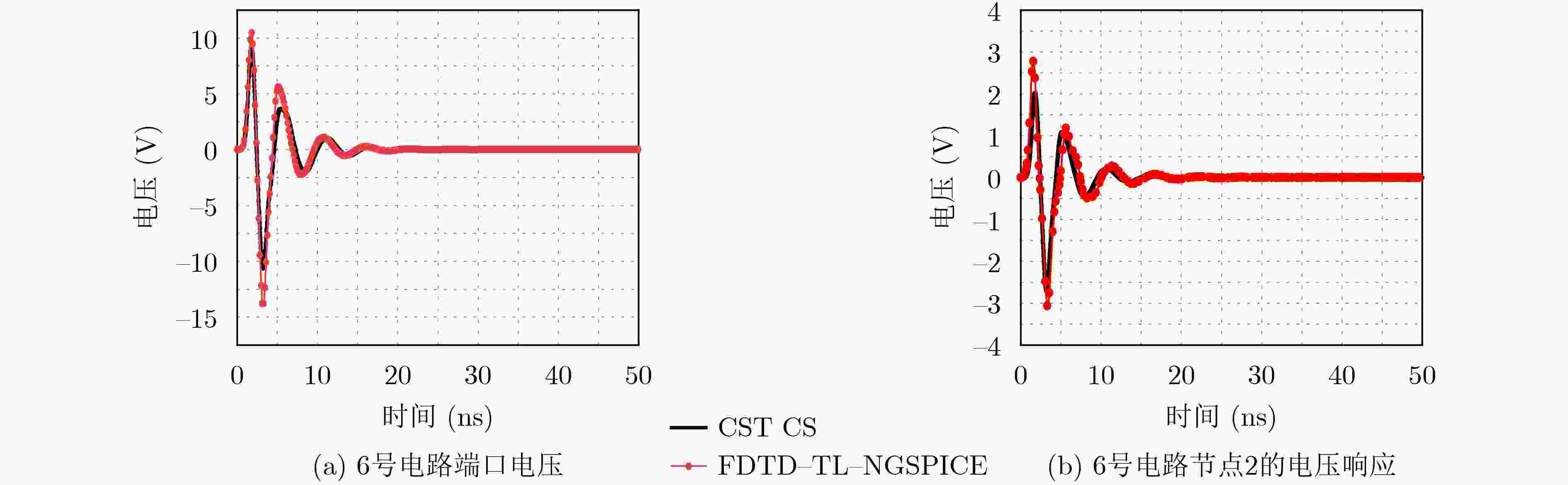
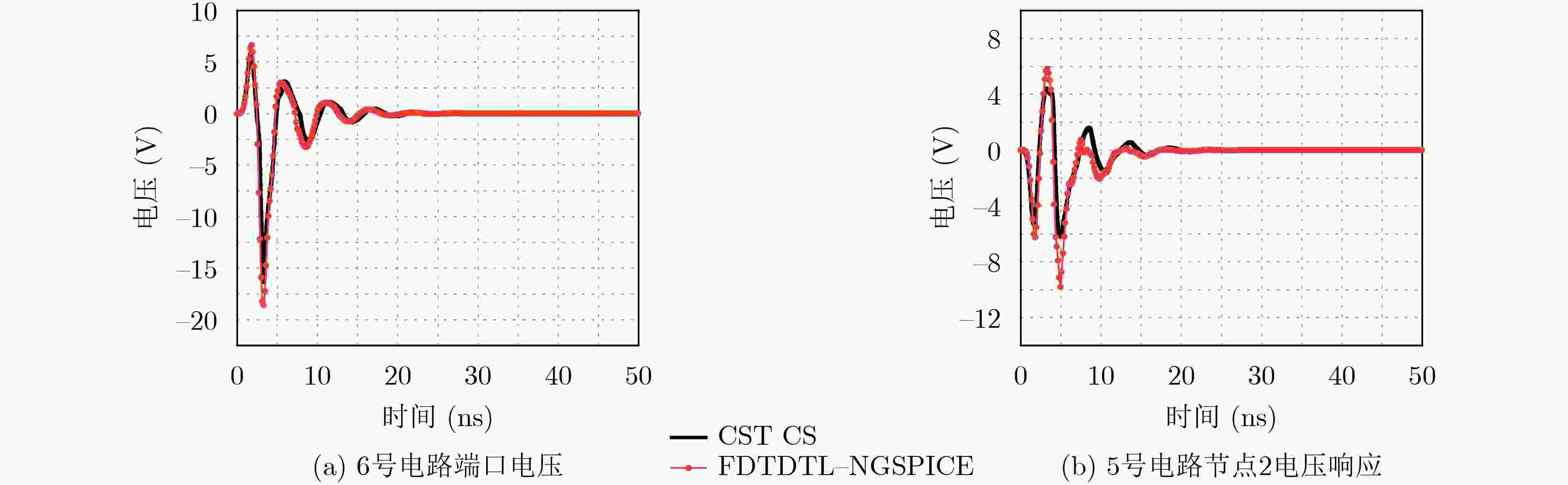
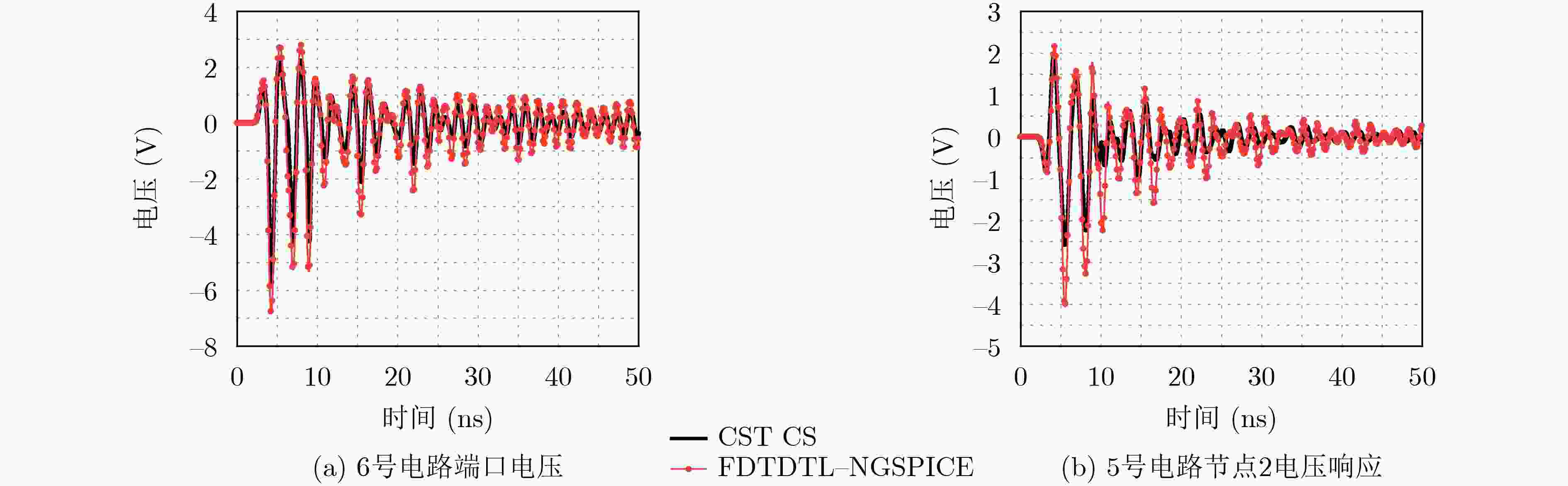
摘要: 针对端接复杂电路传输线(TL)网络的电磁耦合问题,仍缺乏高效的场路协同仿真技术。该文将传输线方程与时域有限差分(FDTD)方法、诺顿定理和置换定理以及NGSPICE软件相结合,并引入消息传递接口(MPI)并行技术,提出一种高效的时域混合并行算法(FDTDTL-NGSPICE)。首先,根据诺顿定理和置换定理,将传输线网络分解为传输线子系统和复杂电路子系统,并构建对应的等效电路模型。然后,使用FDTDTL并行算法计算传输线子系统沿线各点的电压和电流,并获取对应诺顿等效电路的电流源和等效导纳大小。最后,使用NGSPICE对复杂电路子系统进行传导干扰分析,获得复杂电路各元件上的瞬态响应,并将端口电压反馈给传输线子系统作为边界,实现传输线网络电磁耦合的场线路联合协同仿真。通过对3类典型场景的计算实例,分别使用时域混合并行算法和电磁仿真软件CST电缆工作室(CS)进行数值模拟并对比,验证所提算法的置信度。
-
关键词:
- 传输线网络 /
- 复杂电路 /
- 诺顿定理 /
- 时域有限差分与传输线方程的混合并行算法 /
- NGSPICE软件
Abstract: Efficient field-circuit synchronous simulation techniques used for the coupling analysis of Transmission Line (TL) network with complex circuits excited by ambient wave are still rare. In this work, the TL equations are combined with the Norton’s theorem, the Substitution theorem Finite-Difference Time-Domain (FDTD) method, NGSPICE software and parallel technique based on Message Passing Interface (MPI) to form an efficient parallel time domain hybrid method (FDTD-Transmission Line equation-NGSPICE, FDTDTL-NGSPICE). Firstly, the overall structure of transmission line network is decomposed into the transmission line subsystem and complex circuit subsystems according to the Norton’s theorem and Substitution theorem, and the corresponding equivalent circuit models are constructed. Then the parallel FDTDTL method is employed to solve the voltage and current responses along the transmission line subsystem, which are utilized to extract the current sources and equivalent admittance of the Norton’s equivalent circuits. Finally, the NGSPICE software is applied for the conducted interference analysis of the complex circuit subsystems to obtain the transient responses on the ports and all elements of the complex circuits, and then the port voltages are fed back to the transmission line subsystem as boundary conditions. The significant feature of this time domain hybrid method is that it realizes the field-line-circuit synchronous simulation of transmission line network. And the confidence of this method is verified by the comparison of three typical scenario examples simulated by this method and the electromagnetic software CST Cable Studio (CS). -
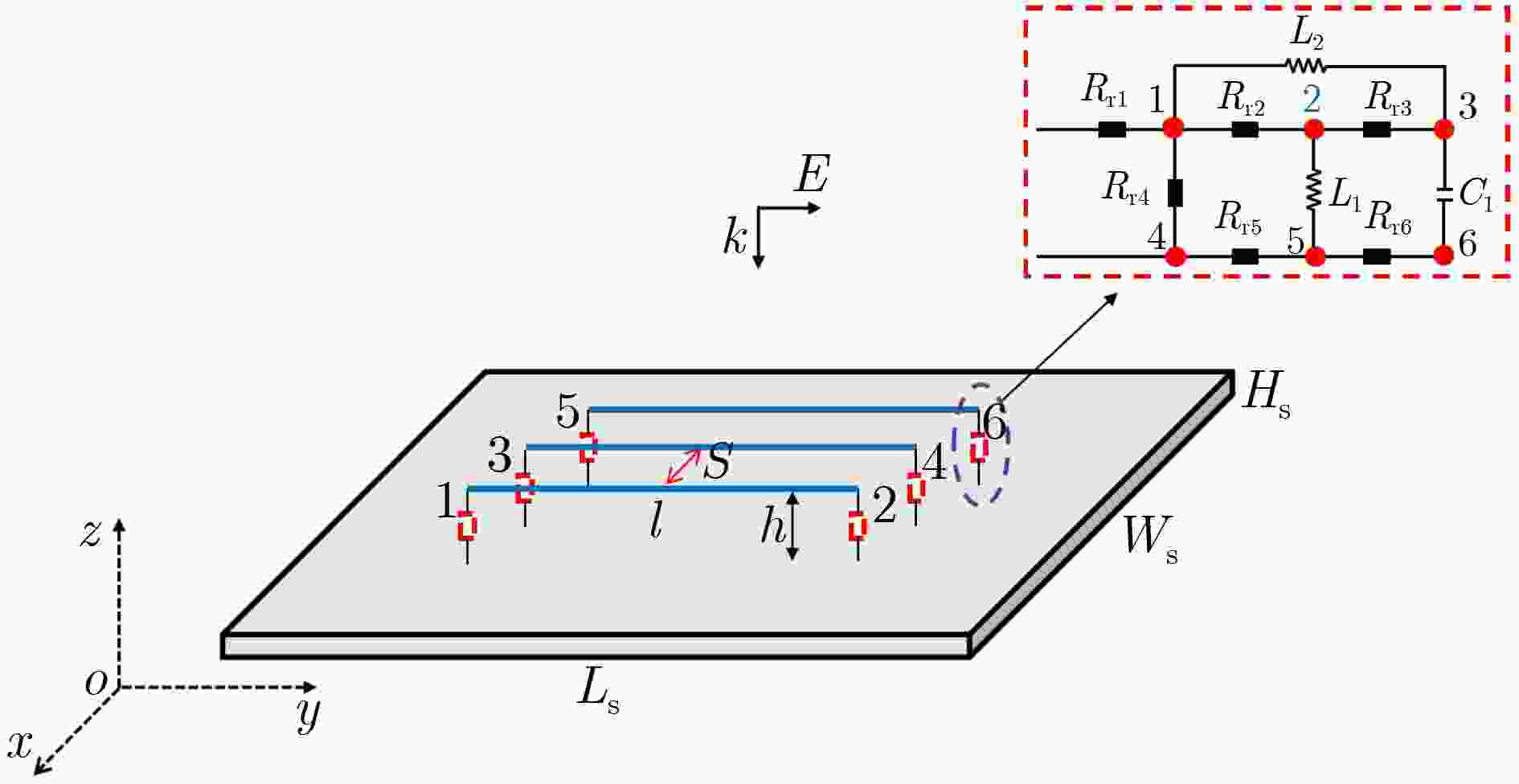
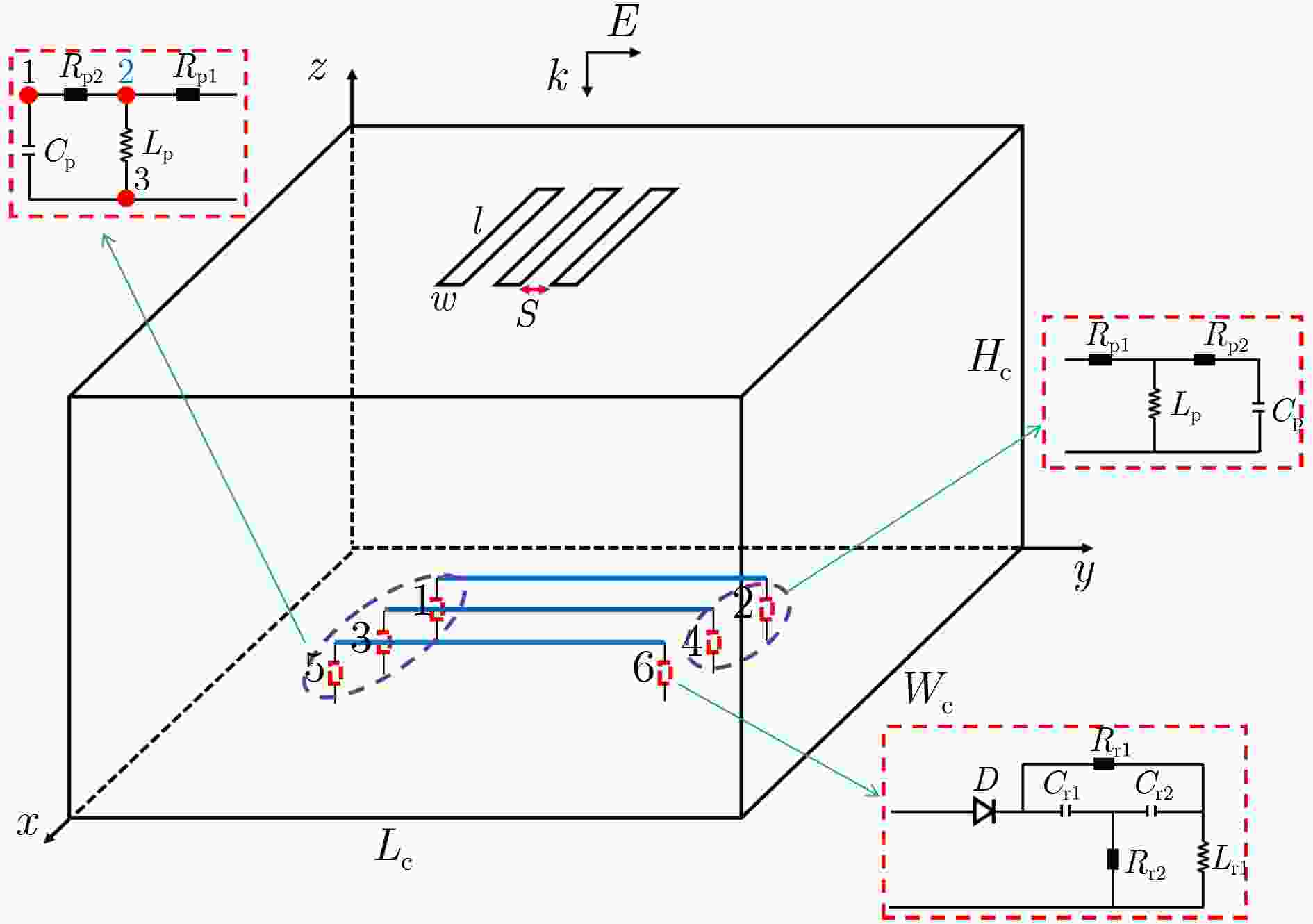
表 1 复杂线性电路的元件参数表
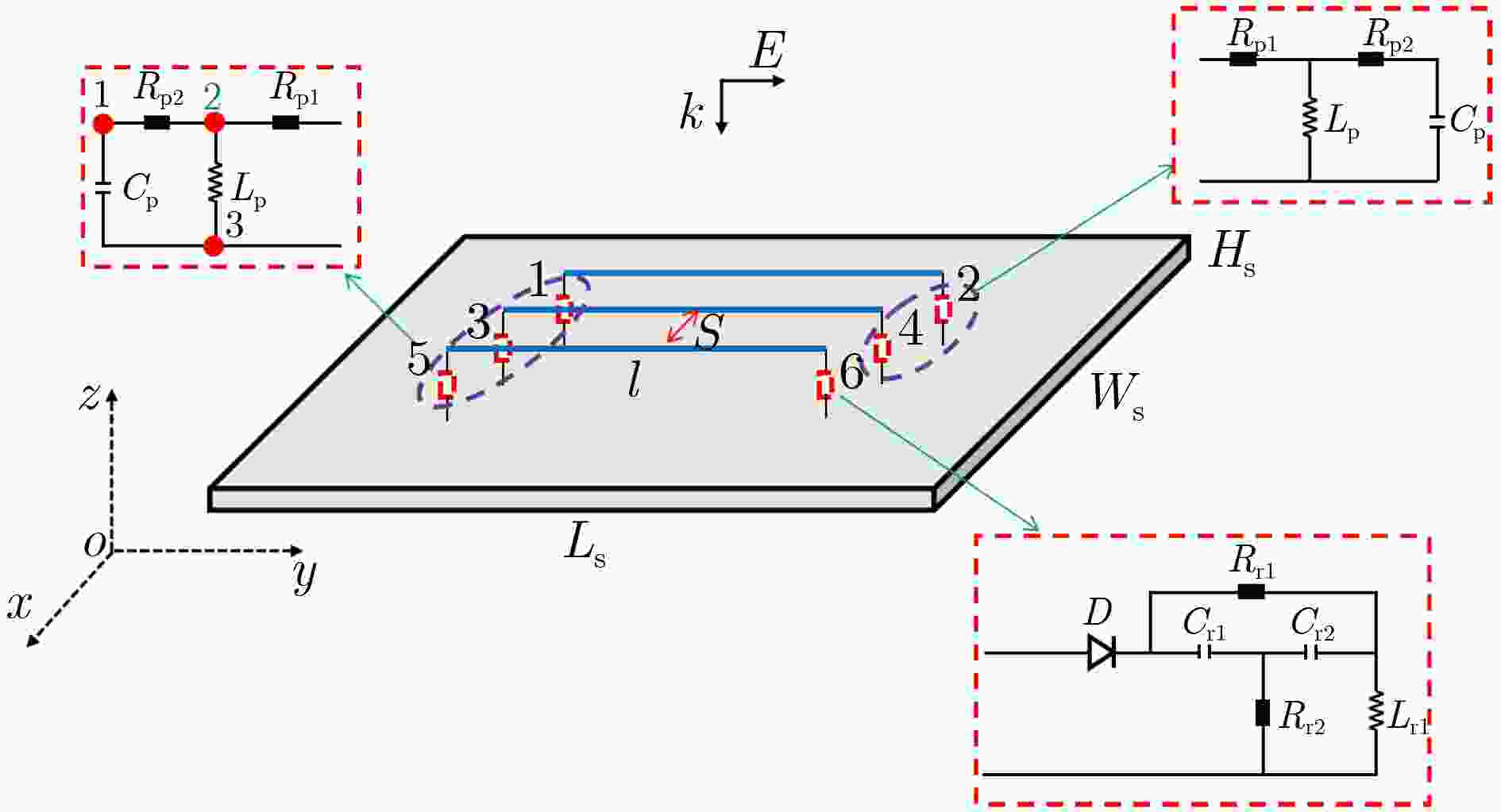
元件 Rr1 Rr2 Rr3 Rr4 Rr5 Rr6 L1 L2 C1 参数值 180 Ω 100 Ω 180 Ω 100 Ω 150 Ω 150 Ω 5 nH 1 nH 1 pF 表 2 复杂非线性电路的元件参数表
元件 Rr1 Rr2 Rp1 Rp2 Cp Cr1 Cr2 Lr1 Lp 参数值 100 Ω 100 Ω 50 Ω 100 Ω 1 pF 1 pF 1 pF 1 nH 1 nH -
[1] XIE Li and LEI Yinzhao. Transient response of a multiconductor transmission line with nonlinear terminations excited by an electric dipole[J]. IEEE Transactions on Electromagnetic Compatibility, 2009, 51(3): 805–810. doi: 10.1109/TEMC.2009.2023327. [2] LI Fulin, HAN Jihong, and ZHANG Chang. Calculation of the electromagnetic pulse effect based on integral equation equivalent circuit and electromagnetic topology[C]. 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 2018: 246–250. doi: 1109/IAEAC.2018.8577741. [3] 罗文君, 赵翔. 基于BLT方程的线性传输线网络自动化分析[J]. 无线电工程, 2018, 48(9): 782–787.LUO Wenjun and ZHAO Xiang. Automated analysis of linear transmission line network based on BLT equation[J]. Radio Engineering, 2018, 48(9): 782–787. [4] YAN Liping, ZHANG Xindan, ZHAO Xiang, et al. A fast and efficient analytical modeling approach for external electromagnetic field coupling to transmission lines in a metallic enclosure[J]. IEEE Access, 2018, 6: 50272–50277. doi: 10.1109/ACCESS.2018.2867686. [5] 王怡, 张馨丹, 甄琦, 等. 平面波照射下贯通导线电磁干扰快速算法[J]. 电波科学学报, 2019, 34(4): 429–435. doi: 10.13443/j.cjors.2018111902.WANG Yi, ZHANG Xindan, ZHEN Qi, et al. Fast algorithm of plane wave coupling to transmission lines penetrating through metallic enclosure[J]. Chinese Journal of Radio Science, 2019, 34(4): 429–435. doi: 10.13443/j.cjors.2018111902. [6] 杨清熙, 周星, 王庆国, 等. 一种有损非均匀传输线时域分析方法[J]. 强激光与粒子束, 2016, 28(1): 113201. doi: 10.11884/HPLPB201628.160154.YANG Qingxi, ZHOU Xing, WANG Qingguo, et al. Equivalent circuit model for transient analysis of lossy non-uniform transmission line network[J]. High Power Laser and Particle Beams, 2016, 28(1): 113201. doi: 10.11884/HPLPB201628.160154. [7] HU Xiao, QIU Yang, XU Linqing, et al. A hybrid FDTD-SPICE method for predicting the coupling response of wireless communication system[J]. IEEE Transactions on Electromagnetic Compatibility, 2021, 63(5): 1530–1541. doi: 10.1109/TEMC.2021.3072282. [8] DU Ziweihua, XIE Yanzhao, DONG Ning, et al. A spice-compatible macromodel for field coupling to underground transmission lines based on the analog behavioral modeling[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(5): 2045–2054. doi: 10.1109/TEMC.2019.2954358. [9] CHEN Hongcai, DU Yaping, YUAN Mengqing, et al. Lightning-induced voltages on a distribution line with surge arresters using a hybrid FDTD–SPICE method[J]. IEEE Transactions on Power Delivery, 2018, 33(5): 2354–2363. doi: 10.1109/TPWRD.2017.2788046. [10] WANG Xuejun, WANG Lixiao, ZHUO Jianliang, et al. A hybrid CN-FDTD-SPICE solver for field-circuit analyses in low-frequency wideband problems[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2020, 10(10): 1721–1728. doi: 10.1109/TCPMT.2020.3020193. [11] YUE Chenshun, WU Yumao, WANG Weijie, et al. Field-circuit simulation based on parallel FDTD-SPICE method[C]. 2021 International Applied Computational Electromagnetics Society (ACES-China) Symposium, Chengdu, China, 2021: 1–2. doi: 10.23919/ACES-China52398.2021.9581704. [12] 王为, 覃宇建, 刘培国, 等. 基于高阶时域有限差分法与改进节点分析法混合求解复杂传输线网络瞬态响应[J]. 电子与信息学报, 2012, 34(12): 2999–3005. doi: 10.3724/SP.J.1146.2012.00160.WANG Wei, QIN Yujian, LIU Peiguo, et al. The solution of transient response for complex transmission line network by hybrid higher order finite difference time domain-modified nodal analysis method[J]. Journal of Electronics & Information Technology, 2012, 34(12): 2999–3005. doi: 10.3724/SP.J.1146.2012.00160. [13] DU Ye, WANG Jian, and XIA Yinshui. A hybrid FDTD method for co-simulation of antenna and rectifier circuit[C]. 2019 IEEE International Conference on Computational Electromagnetics (ICCEM), Shanghai, China, 2019: 1–3. doi: 10.1109/COMPEM.2019.8778937. [14] 叶志红, 苟丹, 吴小林, 等. 传输线端接复杂电路的电磁耦合时域分析方法[J]. 电子与信息学报, 2021, 43(1): 242–248. doi: 10.11999/JEIT191026.YE Zhihong, GOU Dan, WU Xiaolin, et al. Time domain analysis method for the coupling problem of transmission lines terminated with complex circuit[J]. Journal of Electronics & Information Technology, 2021, 43(1): 242–248. doi: 10.11999/JEIT191026. [15] YE Zhihong, XIONG Xiangzheng, LIAO Cheng, et al. A hybrid method for electromagnetic coupling problems of transmission lines in cavity based on FDTD method and transmission line equation[J]. Progress in Electromagnetics Research M, 2015, 42: 85–93. doi: 10.2528/PIERM15032605. [16] LUO Jie, YE Zhihong, and LIAO Cheng. A MPI-based parallel FDTD-TL method for the EMI analysis of transmission lines in cavity excited by ambient wave[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(1): 212–217. doi: 10.1109/TEMC.2019.2896997. -





 下载:
下载:



 下载:
下载:
