一点对多点同时激光通信视轴姿态解算方法

王利辉; 张立中; 孟立新; 白杨杨

doi:10.11999/JEIT221533

一点对多点同时激光通信视轴姿态解算方法

doi: 10.11999/JEIT221533

王利辉^{1, 2, 3},
张立中^{1, 3, ,},
孟立新^{1, 3},
白杨杨^{1, 3}

1.
长春理工大学机电工程学院长春 130022
2.
内蒙古民族大学工学院通辽 028000
3.
长春理工大学空地激光通信技术重点学科实验室长春 130022

基金项目: 国家自然科学基金联合基金项目“叶企孙”科学基金(U2141231)，吉林省教育厅科学技术研究项目(JJKH20210836KJ)

详细信息

作者简介:
王利辉：男，博士研究生，讲师，研究方向为激光通信、捷联惯导、机电系统仿真与测试技术

张立中：男，教授，博士生导师，研究方向为激光通信、精密机械设计、在线检测技术

孟立新：男，副研究员，博士生导师，研究方向为空间激光通信、精密机械设计

白杨杨：男，中级实验师，研究方向为精密伺服控制

通讯作者:
张立中　zlzcust@126.com

中图分类号: TN929.1
计量
- 文章访问数: 496
- HTML全文浏览量: 306
- PDF下载量: 58
- 被引次数: 0
出版历程
- 收稿日期: 2022-12-12
- 修回日期: 2023-03-02
- 网络出版日期: 2023-03-06
- 刊出日期: 2023-08-21

Solution Method of Line-of-sight Attitude in One-point to Multi-point Simultaneous Laser Communication System

WANG Lihui^{1, 2, 3},
ZHANG Lizhong^{1, 3
, ,},
MENG Lixin^{1, 3},
BAI Yangyang^{1, 3}

1.
School of Mechanical and Electrical Engineering, Changchun University of Science and Technology, Changchun 130022, China
2.
College of Engineering, Inner Mongolia University for Nationalities, Tongliao 028000, China
3.
Fundamental Science on Space-Ground Laser Communication Technology Laboratory, Changchun University of Science and Technology, Changchun 130022, China

Funds: Ye Qisun Science Foundation of the Joint Fund of National Natural Science Foundation of China(U2141231), Science and Technology Research Project of Education Department of Jilin Province (JJKH20210836KJ)

摘要

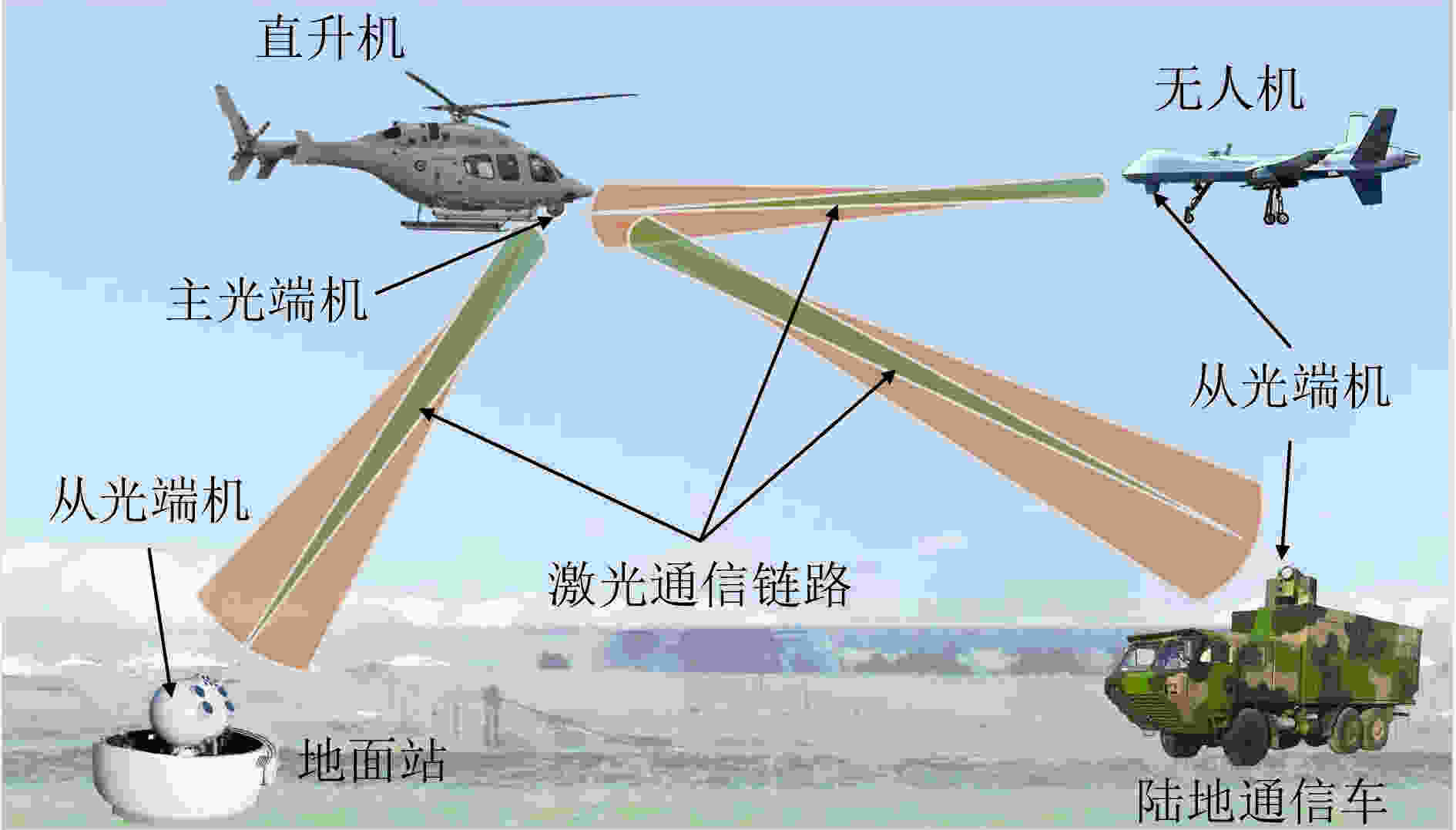
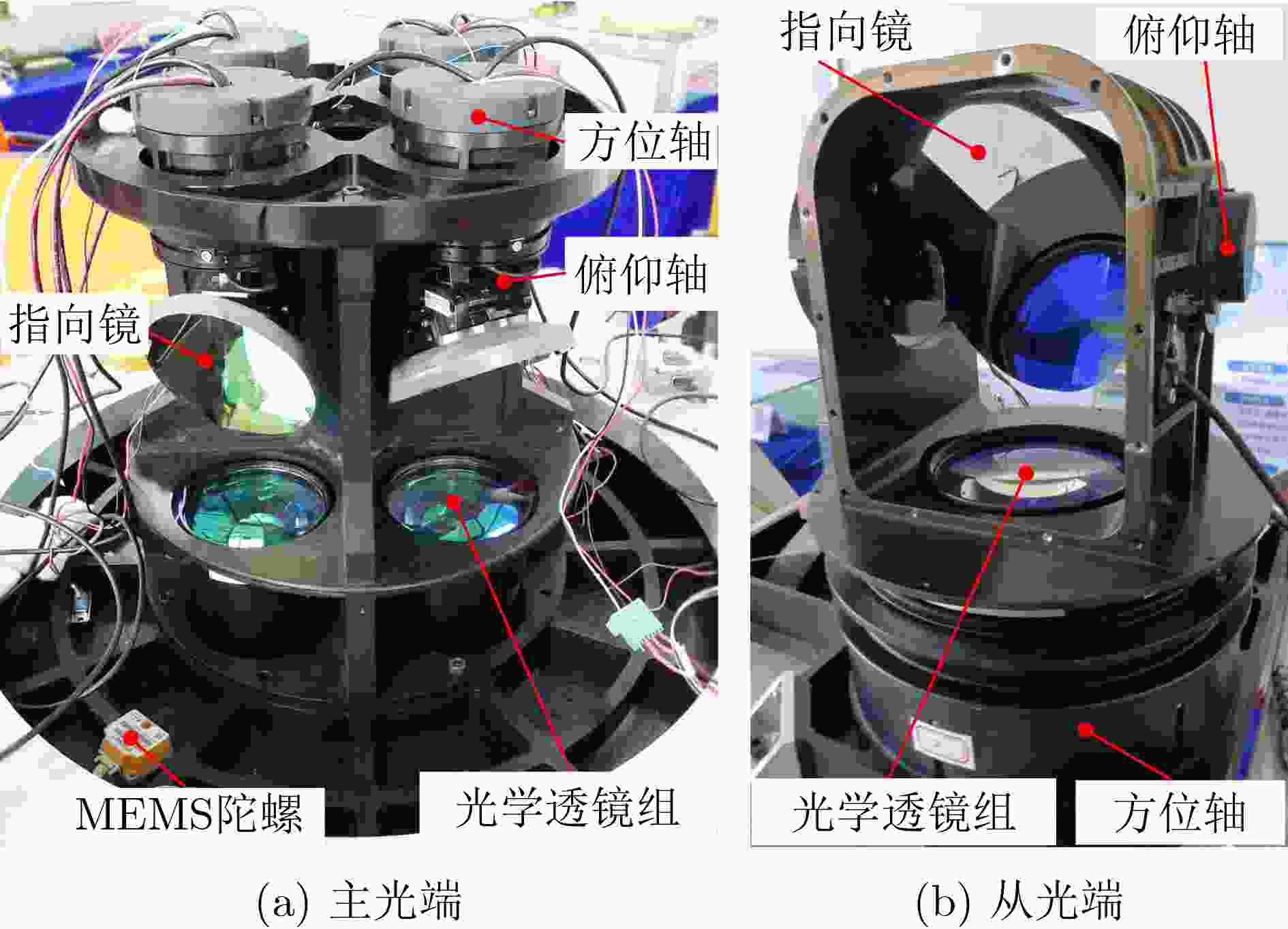
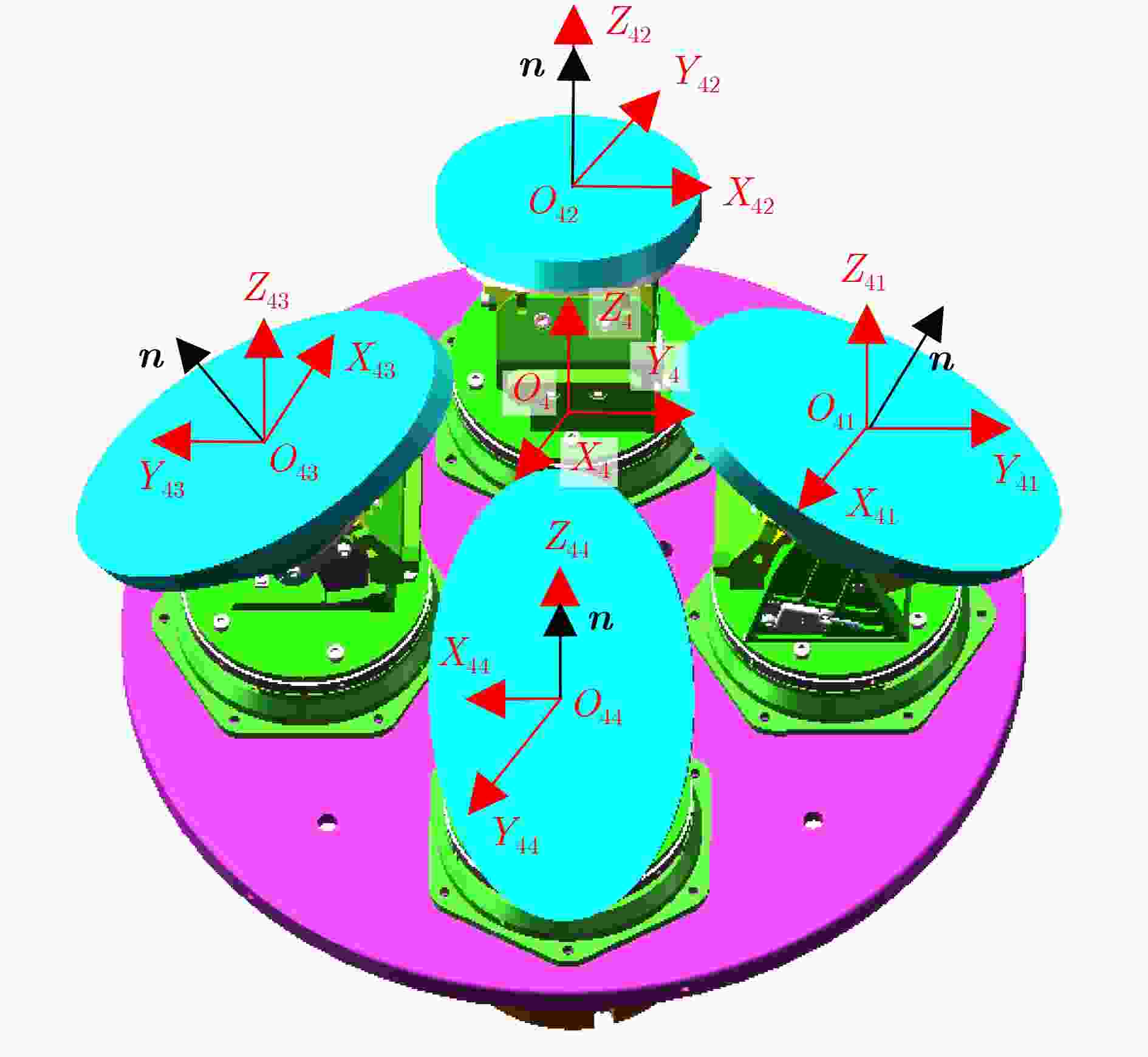
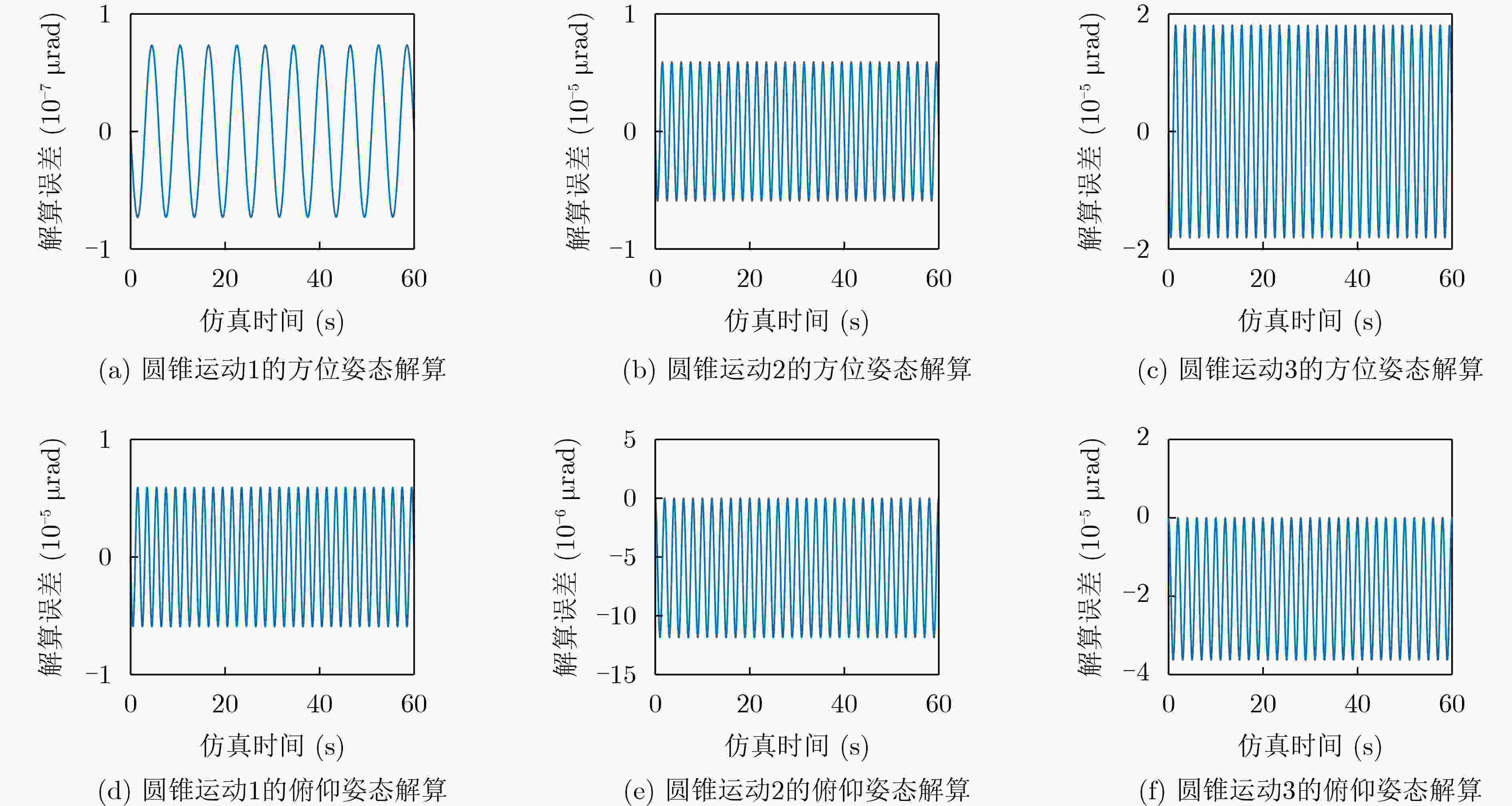
摘要: 针对1点对多点同时激光通信光端机的小型化、轻量化、网络化的技术需求，该文简化了光端机上的多个陀螺，提出一种利用单陀螺实现多个光学视轴同时稳定的方案。为求解多光学视轴姿态，根据欧拉定理重新定义了每个指向镜的坐标系，建立了基于转动4元数的多光学视轴姿态数学模型。为了求解该数学模型的参数，给出了相对应的4阶龙格库塔解算方法，并进行了“三子样”算法优化。最后，将数值解算结果与3种典型圆锥运动的真值进行比较，获得了不同指向镜视轴姿态的解算误差曲线。结果表明，在60 s仿真时间内4阶龙格库塔法对4个光学视轴姿态的联合解算精度优于10^–4 μrad，验证了该模型的有效性。经过“三子样”算法优化后，3种典型圆锥运动的解算精度分别提高了3个数量级、3个数量级和1个数量级，达到了精度优化的目的。该方法的提出，为捷联稳定技术在激光通信组网中的应用提供了理论依据。
- 激光通信 /
- 1点对多点 /
- 转动4元数 /
- 多视轴捷联稳定
Abstract: Considering the technical requirements of one-point to multi-point simultaneous laser communication for miniaturization, light weight and networking of optical transceiver, the multiple gyroscopes on the optical transceiver are simplified, and a scheme of realizing simultaneous stability of multiple optical line-of-sights by using a single gyroscope is proposed. In order to calculate the attitude of multiple optical line-of-sights, the coordinate system of each pointing mirror is redefined according to the Euler theorem, and the mathematical model of multiple optical line-of-sights attitude based on rotating quaternion is established. In order to calculate the parameters of the mathematical model, the fourth-order Runge-Kutta algorithm is given, and the three-sample algorithm is optimized. Finally, the numerical solution results are compared with the true values of three typical cone motions, and the solution error curves of different pointing mirror line-of-sight postures are obtained. The results show that the fourth-order Runge-Kutta method is superior to 10^-4 μrad in the simulation time of 60 s, which verifies the effectiveness of the model. After the optimization of the three-sample algorithm, the accuracy of the joint solution of three typical conical motions is improved by 3 orders of magnitude, 3 orders of magnitude and 1 order of magnitude respectively, and the purpose of accuracy optimization is achieved. This method provides a theoretical basis for the application of strapdown stabilization technology to laser communication networking.
- Laser communication /
- One-point to multi-point /
- Rotating quaternion /
- Multiple optical line-of-sights strapdown stability

HTML全文

图 1 1点对多点同时激光通信组网示意图

下载: 全尺寸图片幻灯片

图 2 1点对4点同时激光通信组网实验

下载: 全尺寸图片幻灯片

图 3 光端机实物示意图

下载: 全尺寸图片幻灯片

图 4 光端机多指向镜坐标系分布图

下载: 全尺寸图片幻灯片

图 5 4阶龙格库塔法数值解算误差曲线

下载: 全尺寸图片幻灯片

图 6 坐标系O₄₁X₄₁Y₄₁Z₄₁内“三子样”算法数值解算误差

下载: 全尺寸图片幻灯片

图 7 坐标系O₄₂X₄₂Y₄₂Z₄₂内“三子样”数值解算误差曲线

下载: 全尺寸图片幻灯片

图 8 坐标系O₄₃X₄₃Y₄₃Z₄₃内“三子样”数值解算误差曲线

下载: 全尺寸图片幻灯片

图 9 坐标系O₄₄X₄₄Y₄₄Z₄₄内“三子样”数值解算误差曲线

下载: 全尺寸图片幻灯片

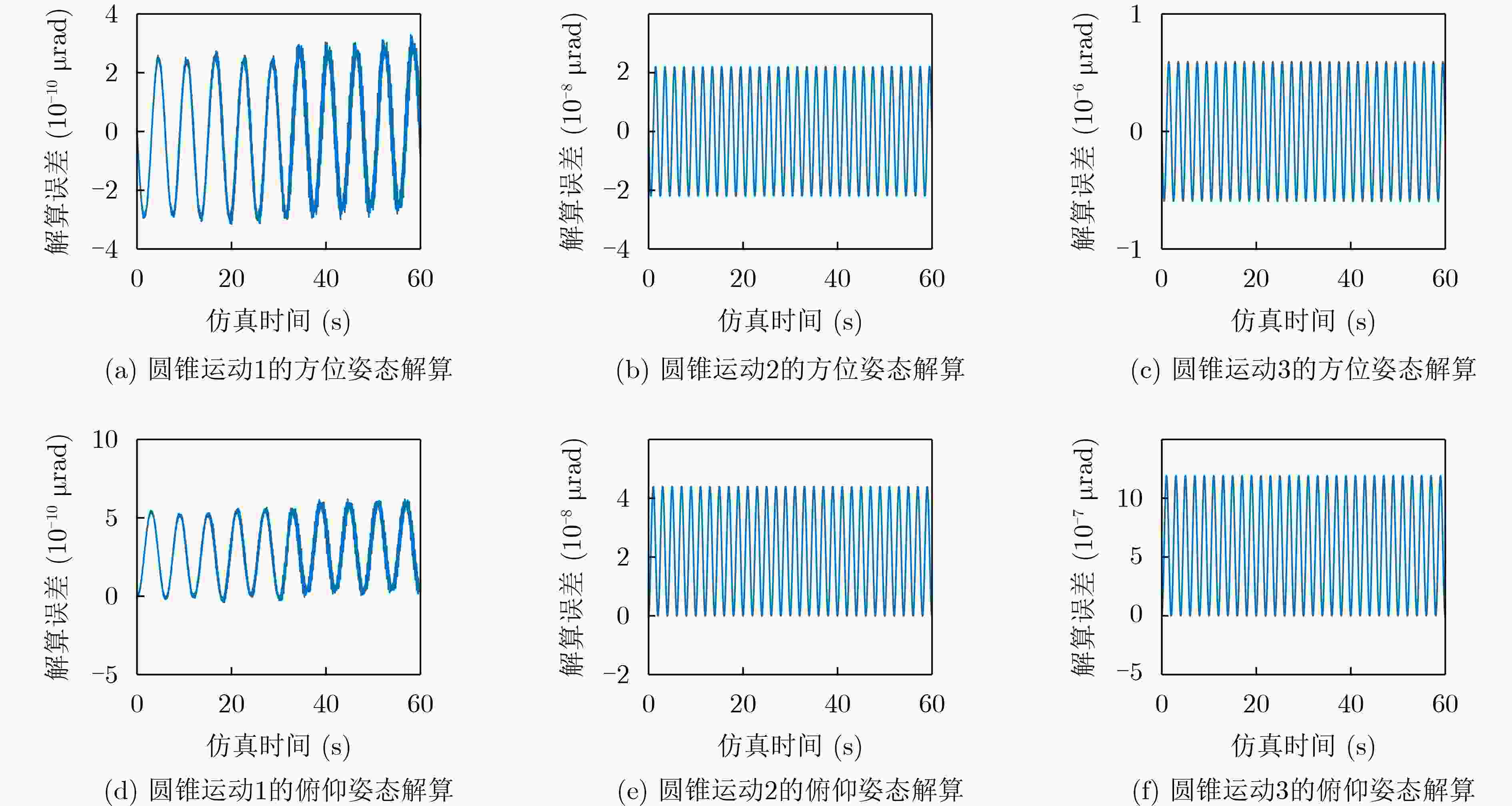
表 1 4阶龙格库塔法数值解算误差

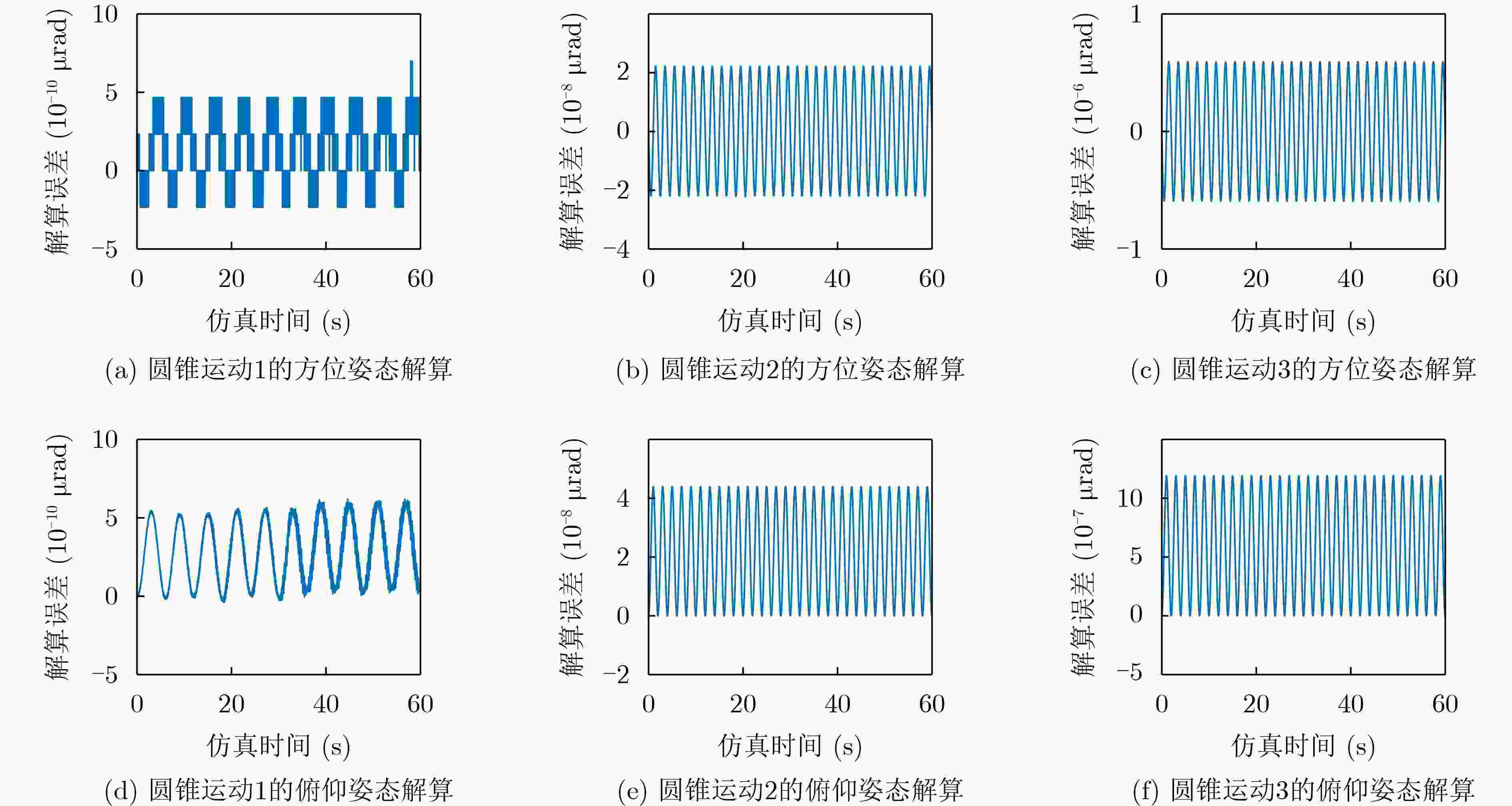
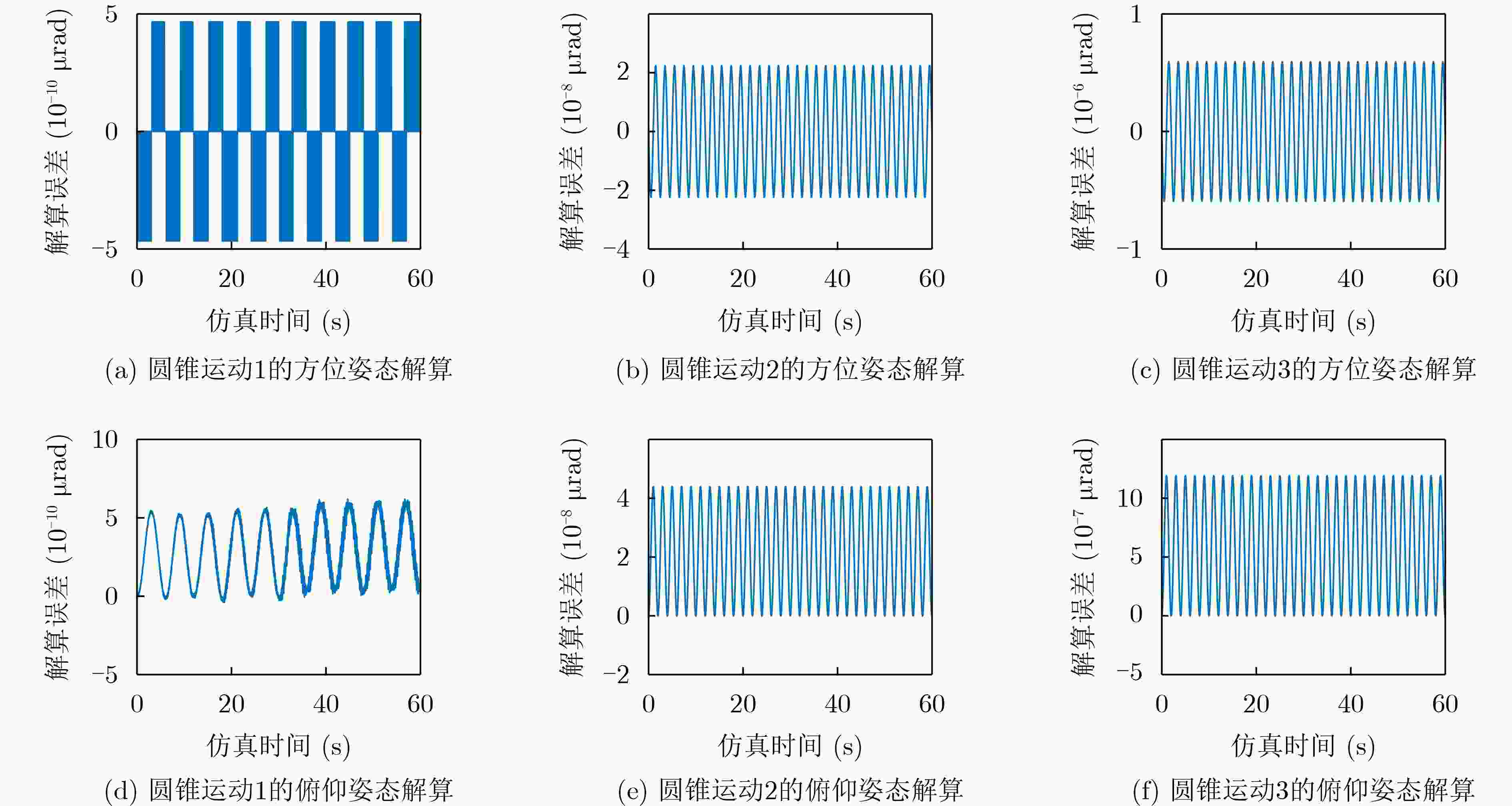
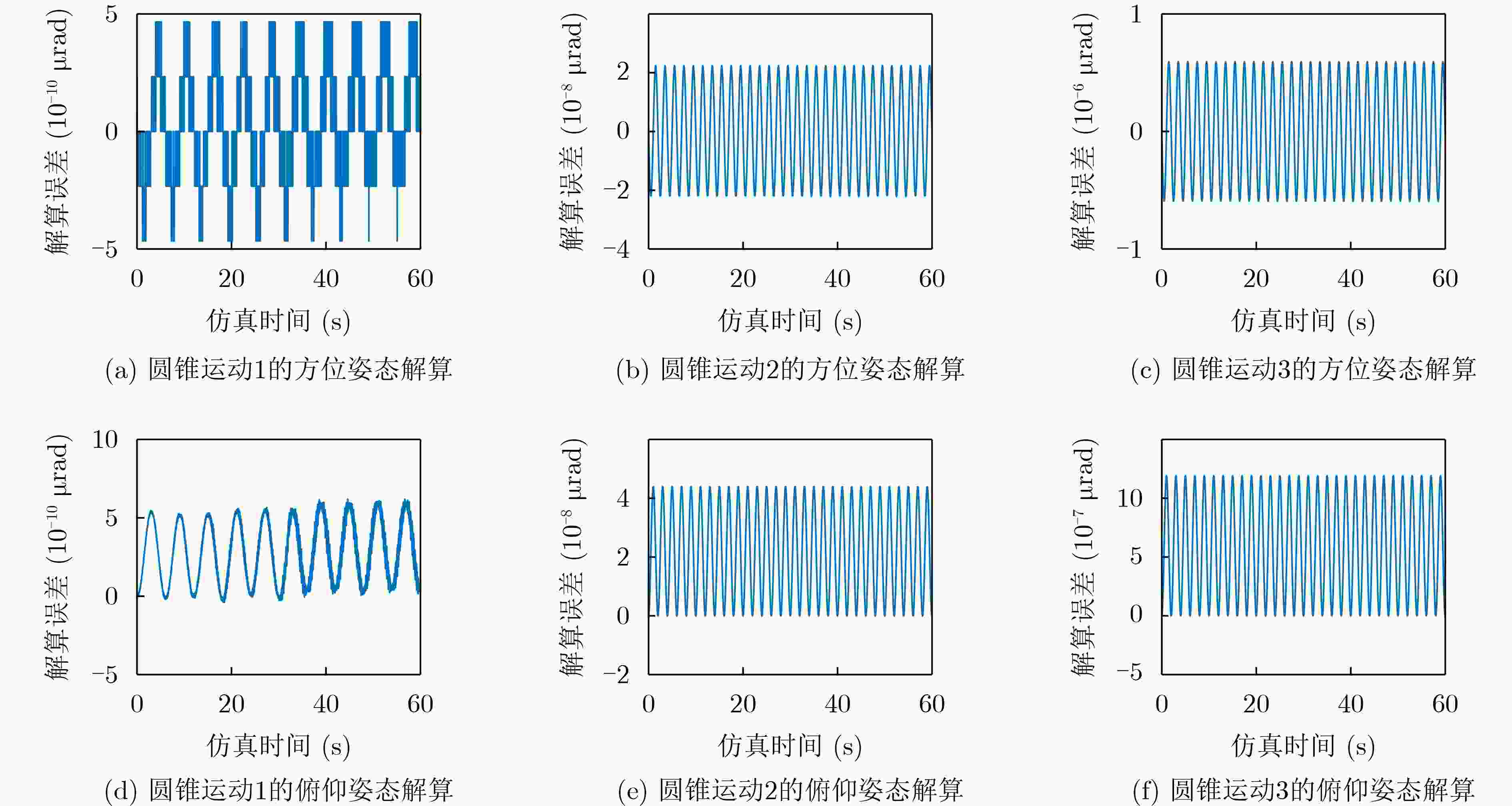
圆锥运动	解算姿态	误差(μrad)
圆锥运动1	方位	7.3×10^–8
圆锥运动1	俯仰	1.5×10^–7
圆锥运动2	方位	5.9×10^–6
圆锥运动2	俯仰	1.2×10^–5
圆锥运动3	方位	1.8×10^–5
圆锥运动3	俯仰	3.6×10^–5

下载: 导出CSV

表 2 “三子样”优化算法数值解算误差(μrad)

指向镜坐标系	姿态	圆锥运动1	圆锥运动2	圆锥运动3
O₄₁X₄₁Y₄₁Z₄₁	方位	3.3×10^–10	2.2×10^–8	5.9×10^–7
O₄₁X₄₁Y₄₁Z₄₁	俯仰	6.2×10^–10	4.4×10^–8	1.2×10^–6
O₄₂X₄₂Y₄₂Z₄₂	方位	7×10^–10	2.2×10^–8	5.9×10^–7
O₄₂X₄₂Y₄₂Z₄₂	俯仰	6.2×10^–10	4.4×10^–8	1.2×10^–6
O₄₃X₄₃Y₄₃Z₄₃	方位	4.7×10^–10	2.2×10^–8	5.9×10^–7
O₄₃X₄₃Y₄₃Z₄₃	俯仰	6.2×10^–10	4.4×10^–8	1.2×10^–6
O₄₄X₄₄Y₄₄Z₄₄	方位	4.7×10^–10	2.2×10^–8	5.9×10^–7
O₄₄X₄₄Y₄₄Z₄₄	俯仰	6.2×10^–10	4.4×10^–8	1.2×10^–6

下载: 导出CSV

参考文献(13)

[1]	WANG Chao, ZHANG Tao, TONG Shoufeng, et al. Pointing and tracking errors due to low-frequency deformation in inter-satellite laser communication[J]. Journal of Modern Optics, 2019, 66(4): 430–437. doi: 10.1080/09500340.2018.1538467
[2]	CHAUDHRY A U and YANIKOMEROGLU H. Laser intersatellite links in a starlink constellation: A classification and analysis[J]. IEEE Vehicular Technology Magazine, 2021, 16(2): 48–56. doi: 10.1109/MVT.2021.3063706
[3]	LI Rui, LIN Baojun, LIU Yingchun, et al. A survey on laser space network: Terminals, links, and architectures[J]. IEEE Access, 2022, 10: 34815–34834. doi: 10.1109/ACCESS.2022.3162917
[4]	徐常志, 靳一, 李立, 等. 面向6G的星地融合无线传输技术[J]. 电子与信息学报, 2021, 43(1): 28–36. doi: 10.11999/JEIT200363 XU Changzhi, JIN Yi, LI Li, et al. Wireless transmission technology of satellite-terrestrial integration for 6G mobile communication[J]. Journal of Electronics &Information Technology, 2021, 43(1): 28–36. doi: 10.11999/JEIT200363
[5]	高铎瑞, 李天伦, 孙悦, 等. 空间激光通信最新进展与发展趋势[J]. 中国光学, 2018, 11(6): 901–913. doi: 10.3788/CO.20181106.0901 GAO Duorui, LI Tianlun, SUN Yue, et al. Latest developments and trends of space laser communication[J]. Chinese Optics, 2018, 11(6): 901–913. doi: 10.3788/CO.20181106.0901
[6]	ROSS M. Unique multiaccess laser communications transciever system[C]. SPIE 1218, Free-Space Laser Communication Technologies II, Los Angeles, USA, 1990: 585–596.
[7]	姜会林, 胡源, 丁莹, 等. 空间激光通信组网光学原理研究[J]. 光学学报, 2012, 32(10): 1006003. doi: 10.3788/AOS201232.1006003 JIANG Huilin, HU Yuan, DING Ying, et al. Optical principle research of space laser communication network[J]. Acta Optica Sinica, 2012, 32(10): 1006003. doi: 10.3788/AOS201232.1006003
[8]	赵佰秋, 于笑楠, 董岩, 等. 空间激光通信组网反射镜跟踪性能[J]. 激光与光电子学进展, 2021, 58(9): 0906007. doi: 10.3788/LOP202158.0906007 ZHAO Baiqiu, YU Xiaonan, DONG Yan, et al. Tracking performance of mirrors in space laser communication networking[J]. Laser &Optoelectronics Progress, 2021, 58(9): 0906007. doi: 10.3788/LOP202158.0906007
[9]	宋江鹏, 孙广利, 周荻, 等. 反射镜光电平台视轴稳定技术研究[J]. 红外与激光工程, 2015, 44(6): 1904–1911. doi: 10.3969/j.issn.1007-2276.2015.06.041 SONG Jiangpeng, SUN Guangli, ZHOU Di, et al. Line-of-sight stabilization techniques for mirror electro-optical platform[J]. Infrared and Laser Engineering, 2015, 44(6): 1904–1911. doi: 10.3969/j.issn.1007-2276.2015.06.041
[10]	王琦, 孙广利, 黎纯宁, 等. 基于半捷联方式的反射镜视轴稳定技术[J]. 红外与激光工程, 2015, 44(10): 3070–3075. doi: 10.3969/j.issn.1007-2276.2015.10.035 WANG Qi, SUN Guangli, LI Chunning, et al. Inertial line-of-sight stabilization technique of semi-strapdown control using mirrors[J]. Infrared and Laser Engineering, 2015, 44(10): 3070–3075. doi: 10.3969/j.issn.1007-2276.2015.10.035
[11]	张荣辉, 贾宏光, 陈涛, 等. 基于四元数法的捷联式惯性导航系统的姿态解算[J]. 光学精密工程, 2008, 16(10): 1963–1970. doi: 10.3321/j.issn:1004-924X.2008.10.029 ZHANG Ronghui, JIA Hongguang, CHEN Tao, et al. Attitude solution for strapdown inertial navigation system based on quaternion algorithm[J]. Optics and Precision Engineering, 2008, 16(10): 1963–1970. doi: 10.3321/j.issn:1004-924X.2008.10.029
[12]	IGNAGNI M B. Efficient class of optimized coning compensation algorithms[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(2): 424–429. doi: 10.2514/3.21635
[13]	熊丽娟, 朱洪涛, 王志勇, 等. 圆锥运动下几种姿态算法的比较与误差建模[J]. 弹箭与制导学报, 2020, 40(3): 39–44. doi: 10.15892/j.cnki.djzdxb.2020.03.010 XIONG Lijuan, ZHU Hongtao, WANG Zhiyong, et al. Compatison and Error Modeling of Several Altitude Algorithms Under Coning Motion[J]. Journal of Projectiles,Rockets,Missiles and Guidance, 2020, 40(3): 39–44. doi: 10.15892/j.cnki.djzdxb.2020.03.010