Cylindrical SAR imaging Based on a Concentric-square-grid Interpolation Method
-
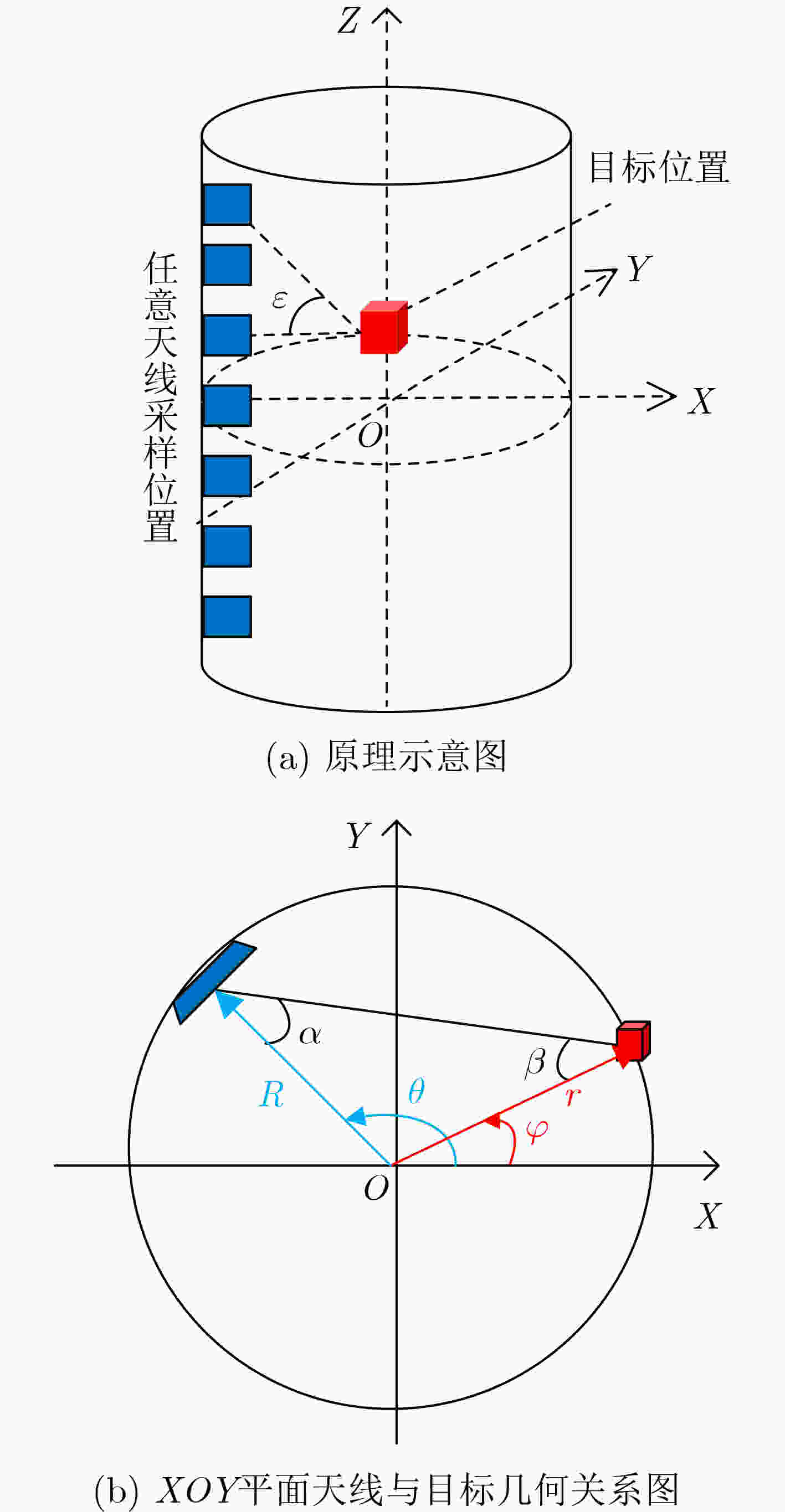
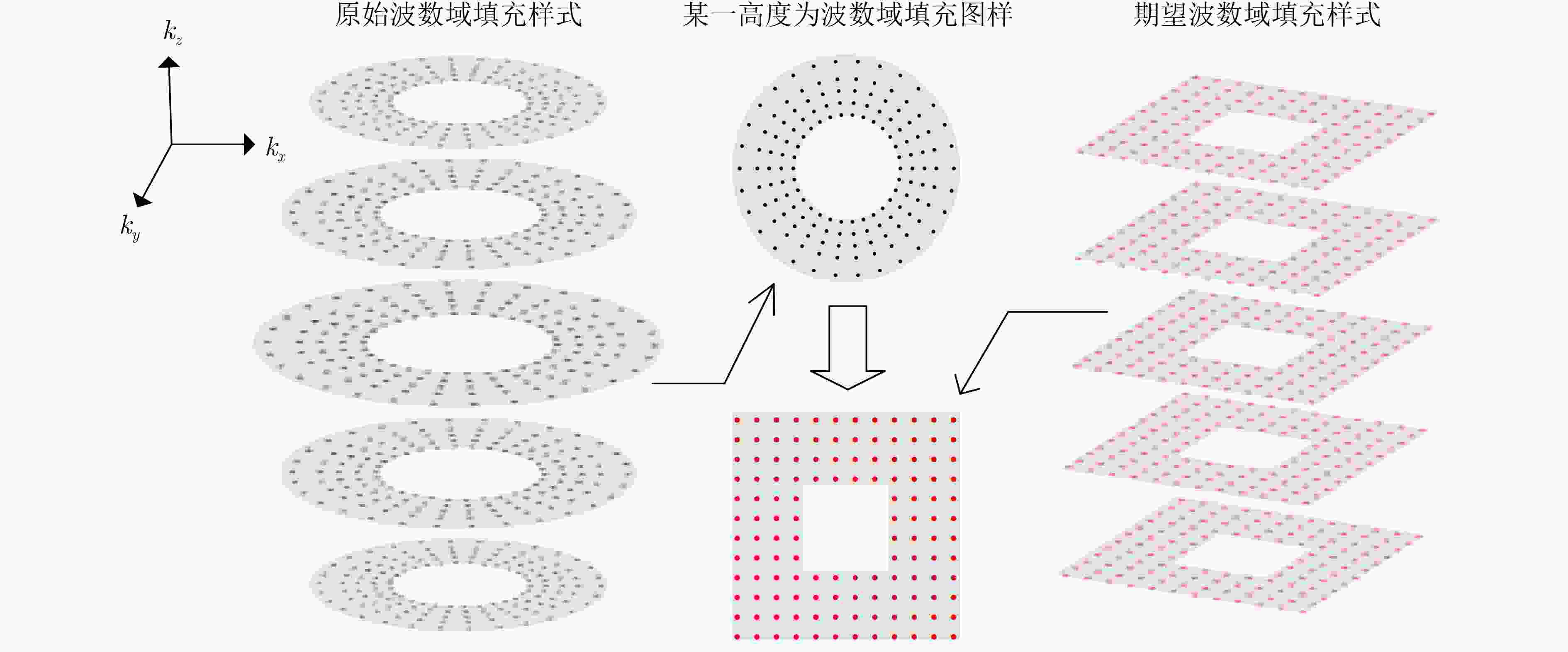
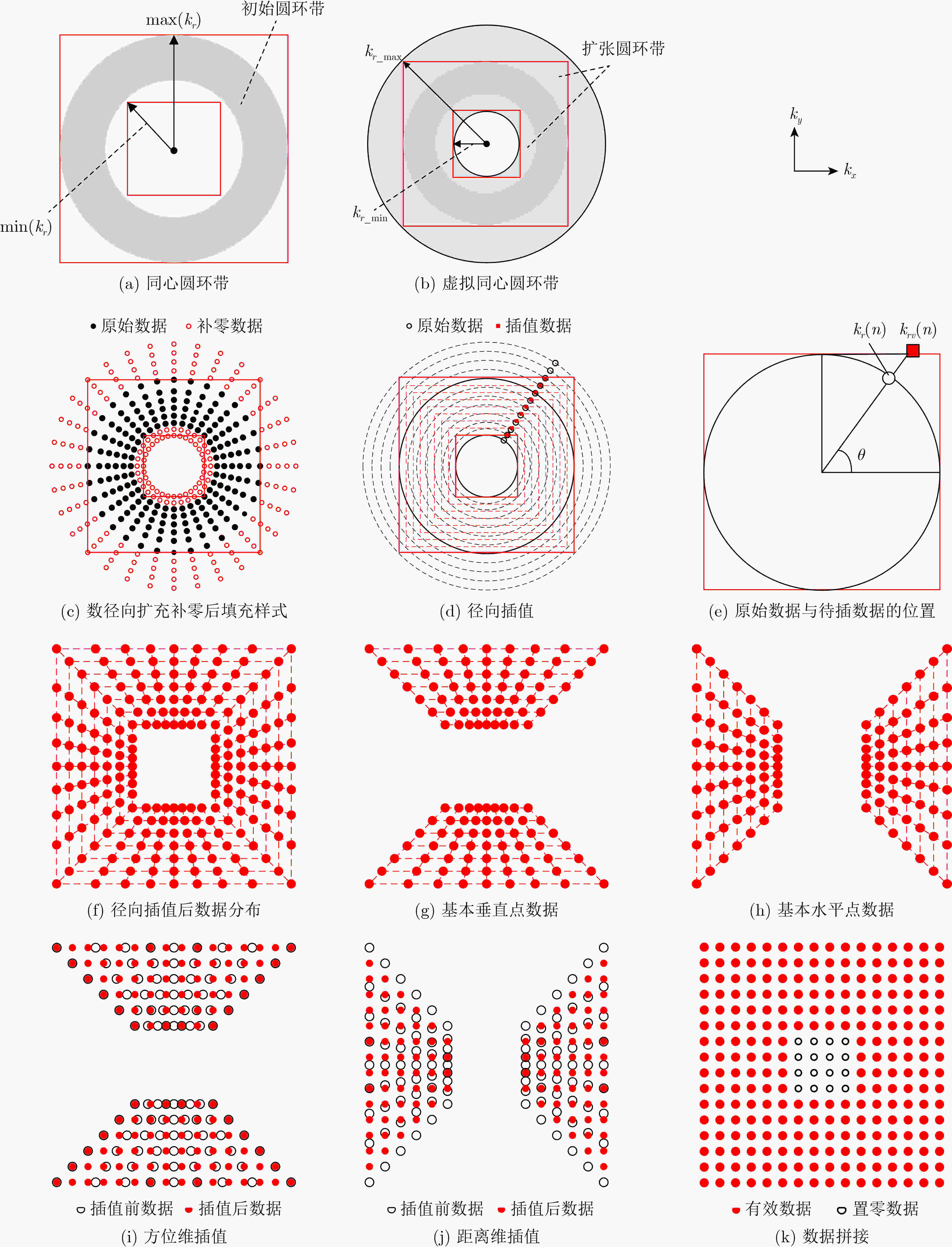
摘要: 柱面毫米波合成孔径雷达(CSAR)是近距离非接触成像领域的重要技术之一。基于傅里叶变换理论的高分辨成像算法需要通过2维插值消除波数域数据在方位维和距离维的非均匀性。但是这两个维度呈现出同心圆环状的高度耦合,导致传统基于2维逐点遍历的插值方法时间复杂度高,成像算法效率低。为此,该文基于解析解的CSAR成像算法推导,提出了同心方形网格的插值分解方法。通过补0、径向1维插值和分区处理消除波数域方位维和距离维的强耦合性,并在两个分区进行独立的1维插值实现2维非均匀波数域的均匀重采样,获得最终同心方形环带均匀填充的波数域样式。通过实验验证了所提算法能有效降低2维插值的时间复杂度,并且所提算法插值处理速度比传统算法提升了7倍,与算法复杂度理论分析结果吻合。Abstract: Cylindrical millimeter-wave Synthetic Aperture Radar (CSAR) is one of the important technologies in the field of close-range non-contact imaging. High-resolution imaging algorithms based on Fourier transform theory require Two-Dimensional (2D) interpolation to eliminate the non-uniformity of wavenumber domain data in both the azimuth and distance dimensions. However, these two dimensions exhibit a high degree of coupling, in the form of a concentric-circle shaped filling in the wavenumber domain. This results in a high temporal complexity of the traditional interpolation method based on a 2D point-by-point traversal, leading to a low efficiency of the imaging algorithm. Therefore, the interpolation decomposition method of concentric square mesh is proposed by deriving the CSAR imaging algorithm based on the analytical solution. Through the zero padding operation, the radial 1D interpolation, and partition, the strong coupling of the azimuth dimension and distance dimension in the wavenumber domain would be eliminated. The uniform resampling of the 2D non-uniform wavenumber domain is achieved by two independent 1D interpolations with respect to two non-overlapping partitions. It yields the expected concentric-square-belt filling shape of the wavenumber domain. Experimental results demonstrate that the proposed method can effectively reduce the time complexity of the straightforward 2D interpolation and increase the efficiency of the imaging algorithm. And the interpolation processing speed of the proposed algorithm is increased by 7 times compared with the traditional algorithm, which is consistent with the theoretical analysis of the algorithm complexity.
-
表 1 实验参数
参数 符号 数值 频率 f 75~110 GHz 频率维点数 Nf 351 角度维点数 Nθ 240 高度维点数 Nz 200 频率维采样间隔 Δf 300 MHz 角度维采样间隔 Δθ 0.25° 高度维采样间隔 Δz 0.0015 m 扫描角度 θ 90° 表 2 点目标成像质量参数
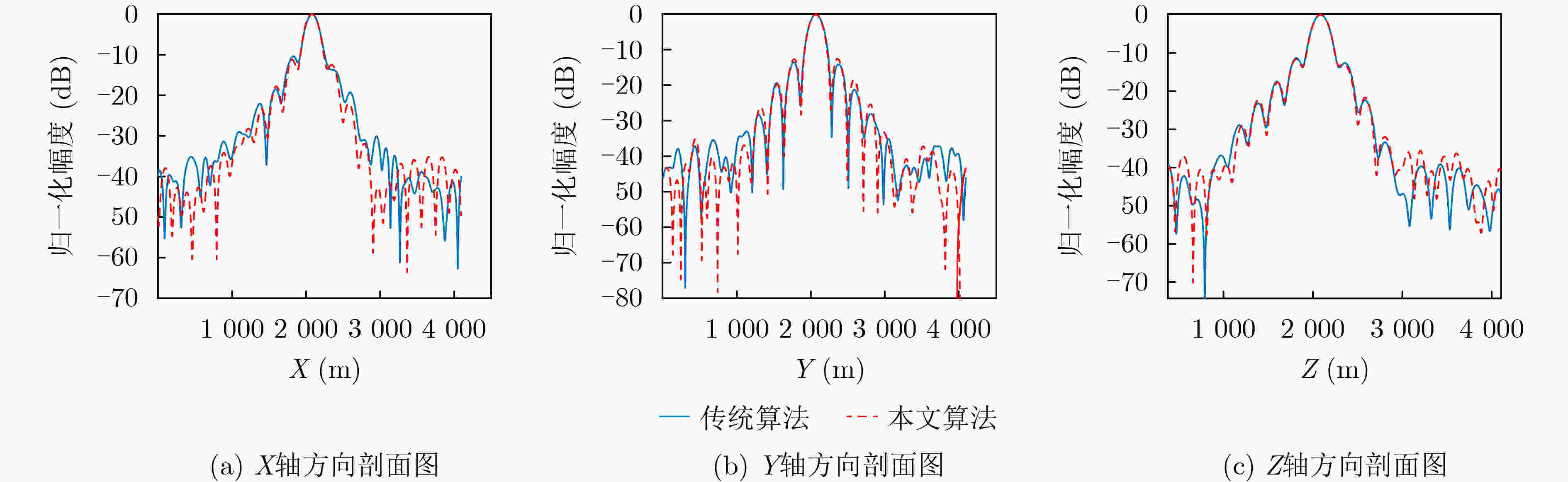
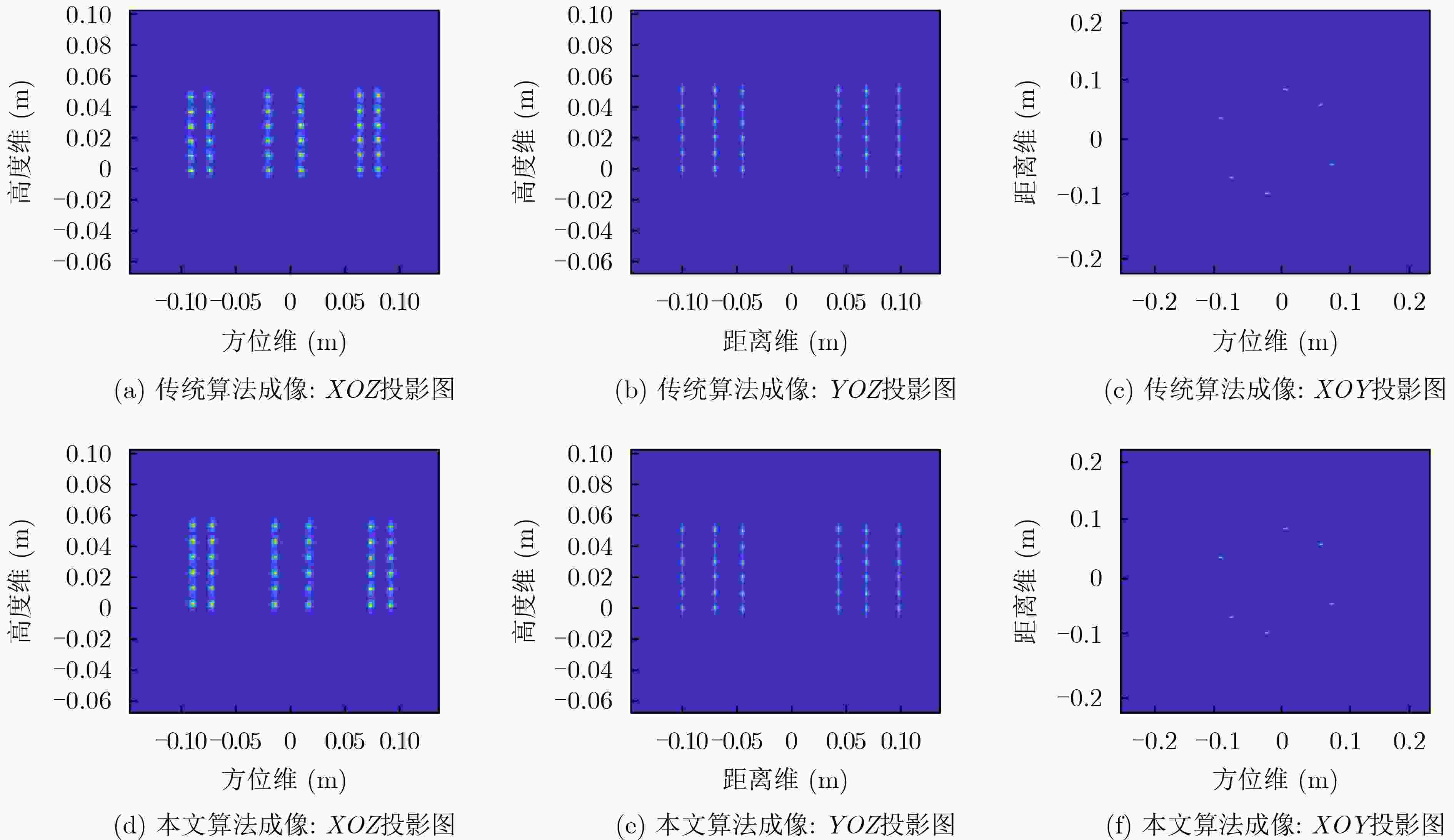
算法 距离维 方位维 高度维 插值时间(s) PSLR(dB) ISLR(dB) 分辨率(m) PSLR(dB) ISLR(dB) 分辨率(m) PSLR(dB) ISLR(dB) 分辨率(m) 改进算法 –11.274 –10.592 0.0043 –12.592 –10.147 0.0055 –11.625 –9.926 0.0058 10.13 传统算法 –10.385 –10.825 0.0045 –13.457 –10.533 0.0054 –11.499 –9.894 0.0059 74.33 表 3 理论运算量与插值处理时间
改进算法 传统算法 插值理论运算量 (GFLOP) 0.369 4.79 插值处理时间 (s) 10.53 74.84 -
[1] 刘燕, 吴元, 孙光才, 等. 圆轨迹SAR快速成像处理[J]. 电子与信息学报, 2013, 35(4): 852–858. doi: 10.3724/SP.J.1146.2012.00607LIU Yan, WU Yuan, SUN Guangcai, et al. Fast imaging processing of circular SAR[J]. Journal of Electronics &Information Technology, 2013, 35(4): 852–858. doi: 10.3724/SP.J.1146.2012.00607 [2] 张健丰, 付耀文, 张文鹏, 等. 圆迹合成孔径雷达成像技术综述[J]. 系统工程与电子技术, 2020, 42(12): 2716–2734. doi: 10.3969/j.issn.1001-506X.2020.12.07ZHANG Jianfeng, FU Yaowen, ZHANG Wenpeng, et al. Review of CSAR imaging techniques[J]. Systems Engineering and Electronics, 2020, 42(12): 2716–2734. doi: 10.3969/j.issn.1001-506X.2020.12.07 [3] DONG Qinghai, WANG Bingnan, XIANG Maosheng, et al. A novel detection scheme in image domain for multichannel circular SAR ground-moving-target indication[J]. Sensors, 2022, 22(7): 2596. doi: 10.3390/S22072596 [4] LI Yishi, CHEN Leping, AN Daoxiang, et al. A novel method for extracting geometric parameter information of buildings based on CSAR images[J]. International Journal of Remote Sensing, 2022, 43(11): 4117–4133. doi: 10.1080/01431161.2022.2106802 [5] 韩冬, 周良将, 焦泽坤, 等. 基于改进三维后向投影的多圈圆迹SAR相干三维成像方法[J]. 电子与信息学报, 2021, 43(1): 131–137. doi: 10.11999/JEIT190945HAN Dong, ZHOU Liangjiang, JIAO Zekun, et al. A coherent 3-D imaging method for multi-circular SAR based on an improved 3-D back projection algorithm[J]. Journal of Electronics &Information Technology, 2021, 43(1): 131–137. doi: 10.11999/JEIT190945 [6] 程添. 针对安检应用的毫米波雷达成像方法研究[D]. [硕士论文], 电子科技大学, 2021.CHENG Tian. Research on the imaging method of millimeter wave radar for security inspection applications[D]. [Master dissertation], University of Electronic Science and Technology of China, 2021. [7] SOUMEKH M. Reconnaissance with slant plane circular SAR imaging[J]. IEEE Transactions on Image Processing, 1996, 5(8): 1252–1265. doi: 10.1109/83.506760 [8] SHEEN D, MCMAKIN D, and HALL T. Near-field three-dimensional radar imaging techniques and applications[J]. Applied Optics, 2010, 49(19): E83–E93. doi: 10.1364/AO.49.000E83 [9] REN Bailing, LI Shiyong, SUN Houjun, et al. Modified cylindrical holographic algorithm for three-dimensional millimeter-wave imaging[J]. Progress in Electromagnetics Research, 2012, 128: 519–537. doi: 10.2528/pier12041619 [10] 朱荣强. 阵列雷达近场三维成像算法研究[D]. [硕士论文], 国防科学技术大学, 2016.ZHU Rongqiang. Near-field three-dimensional imaging algorithm for array-based radar[D]. [Master dissertation], National University of Defense Technology, 2016. [11] TANG Yu, XING Mengdao, and BAO Zheng. The polar format imaging algorithm based on double chirp-Z transforms[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4): 610–614. doi: 10.1109/LGRS.2008.2000971 [12] 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2005: 1–5.HUANG Peikang, YIN Hongcheng, and XU Xiaojian. Rader Target Properties[M]. Beijing: Publishing House of Electronics Industry, 2005: 1–5. [13] 温鑫, 黄培康, 年丰, 等. 主动式毫米波近距离圆柱扫描三维成像系统[J]. 系统工程与电子技术, 2014, 36(6): 1044–1049. doi: 10.3969/j.issn.1001-506X.2014.06.05WEN Xin, HUANG Peikang, NIAN Feng, et al. Active millimeter-wave near-field cylindrical scanning three-dimensional imaging system[J]. Systems Engineering and Electronics, 2014, 36(6): 1044–1049. doi: 10.3969/j.issn.1001-506X.2014.06.05 [14] LETTINGTON A H, HONG Q H, DEAN A, et al. Overview of recent advances in passive millimeter-wave imaging in the UK[C]. SPIE 2744, Infrared Technology and Applications XXII, Orlando, USA, 1996: 146–153. [15] 李薇. ISAR实时成像系统及成像质量评价研究[D]. [硕士论文], 西安电子科技大学, 2020.LI Wei. ISAR real-time imaging system and imaging quality evaluation[D]. [Master dissertation], Xidian University, 2020. -





 下载:
下载:
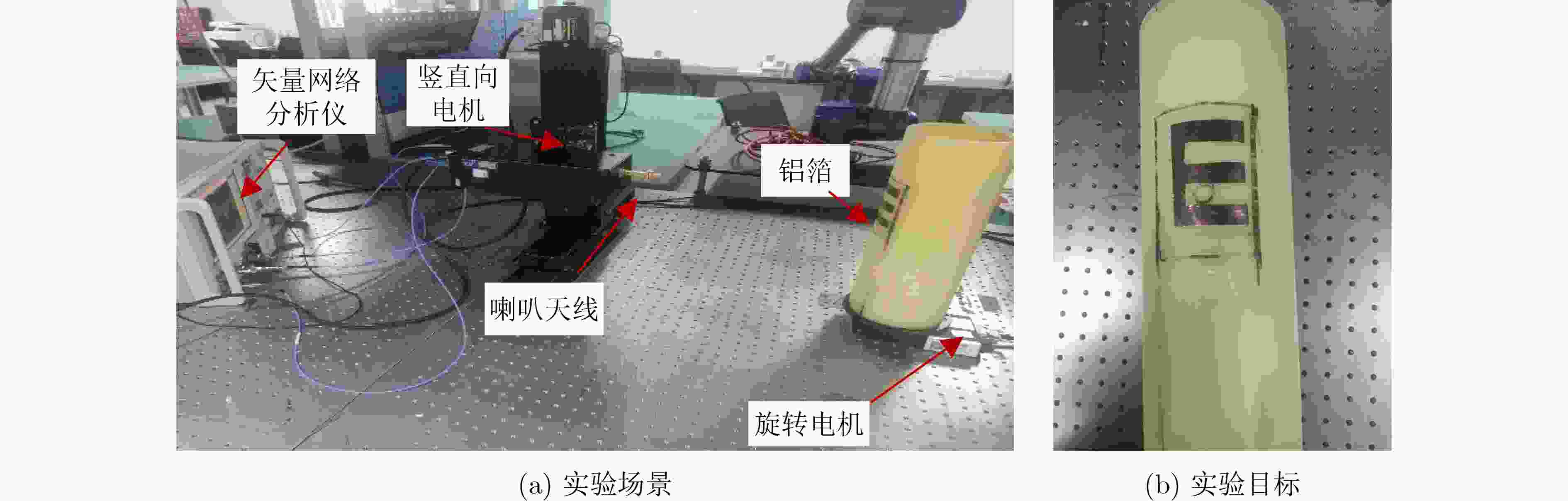
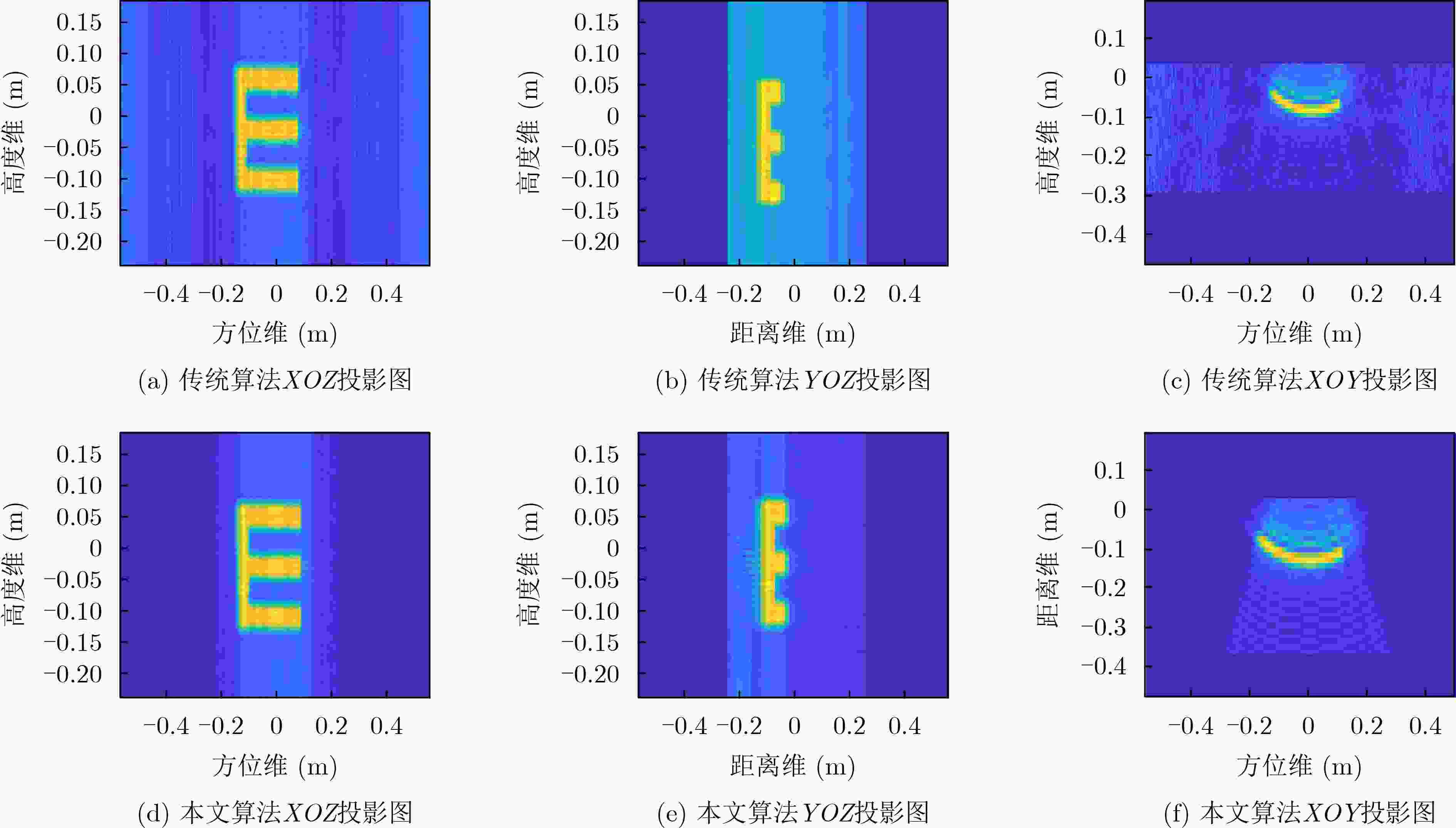


 下载:
下载:
