Research on Relay Selection and Trajectory Optimization in Post-disaster Emergency Communication Network
-
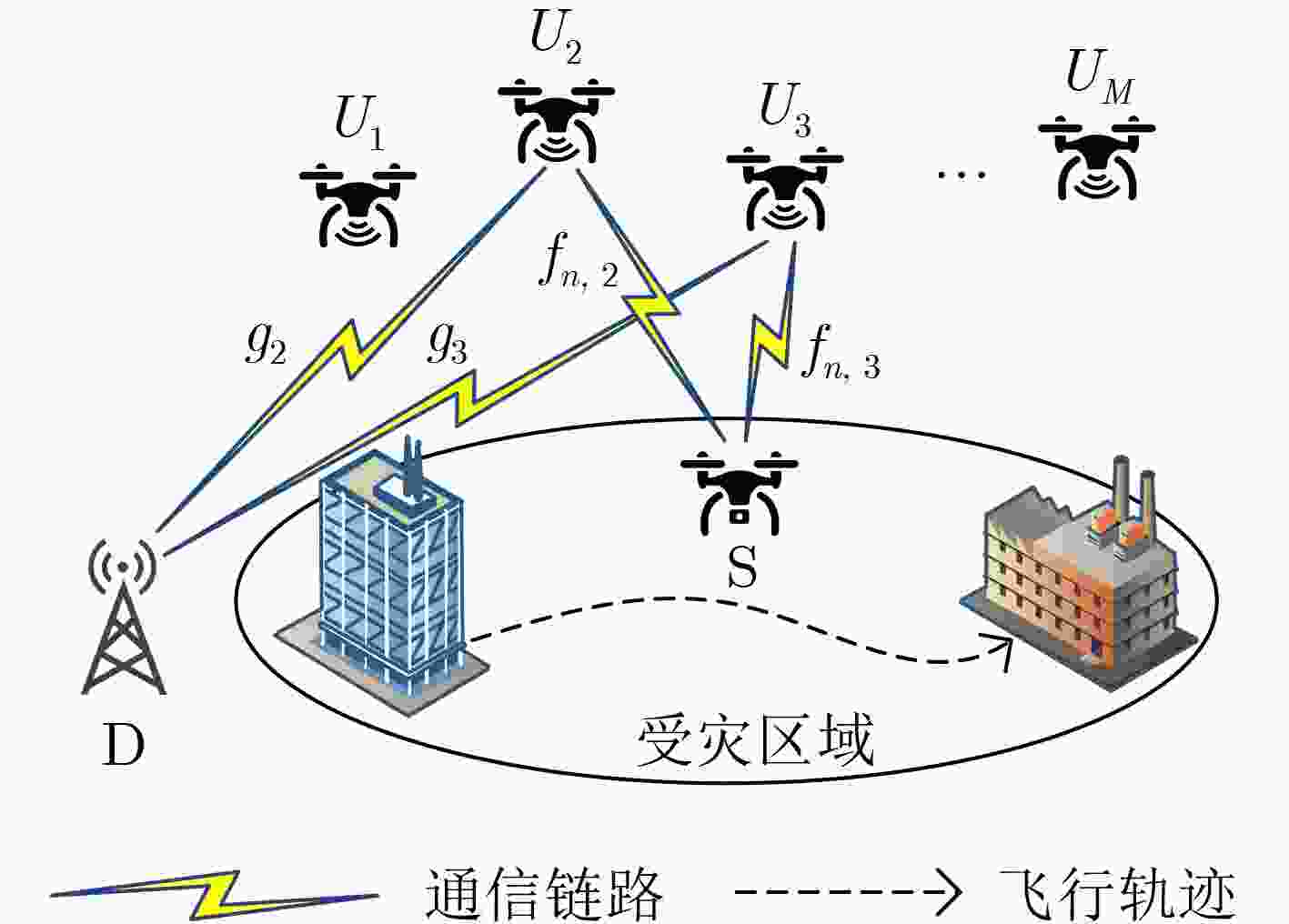
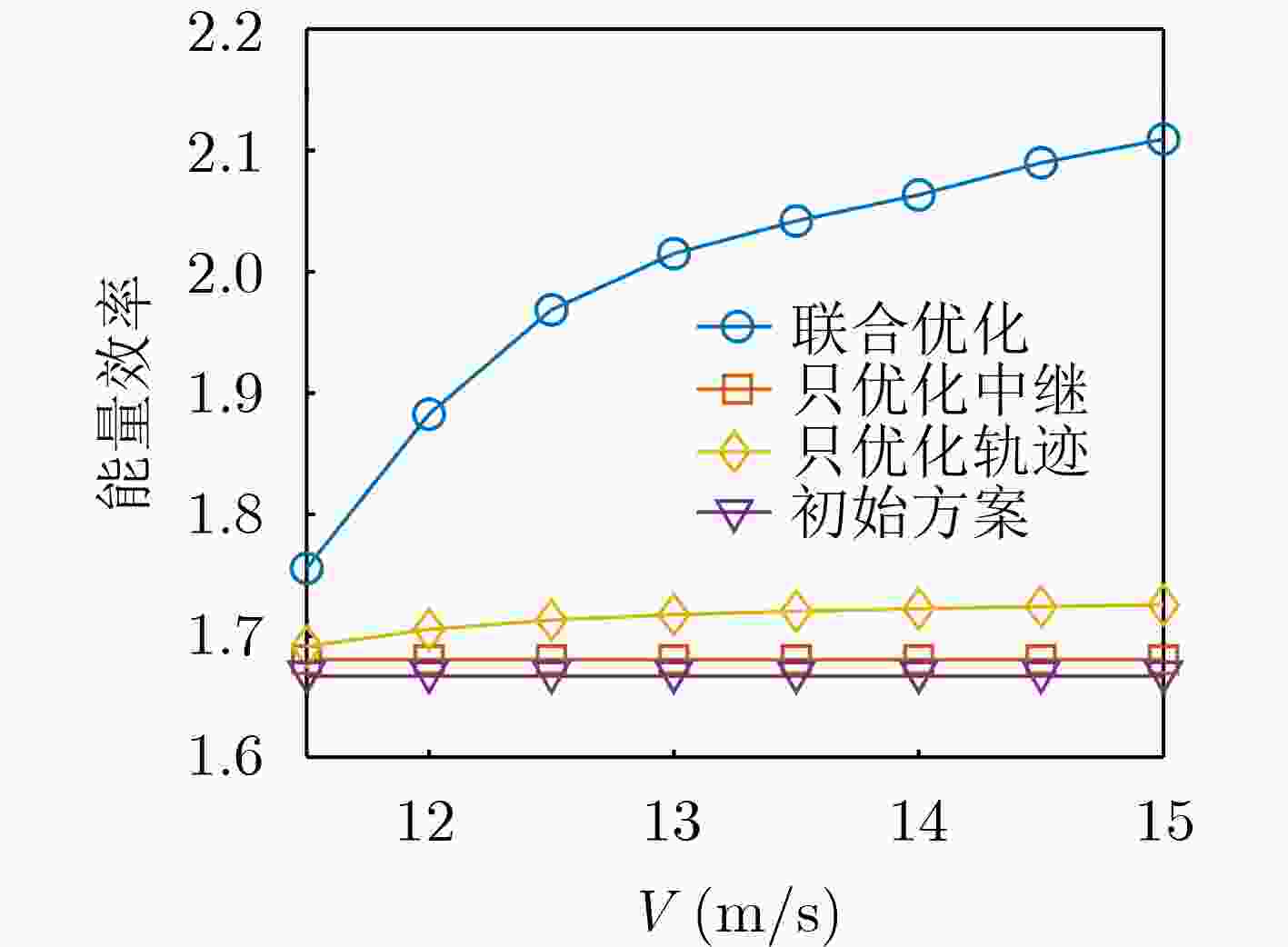
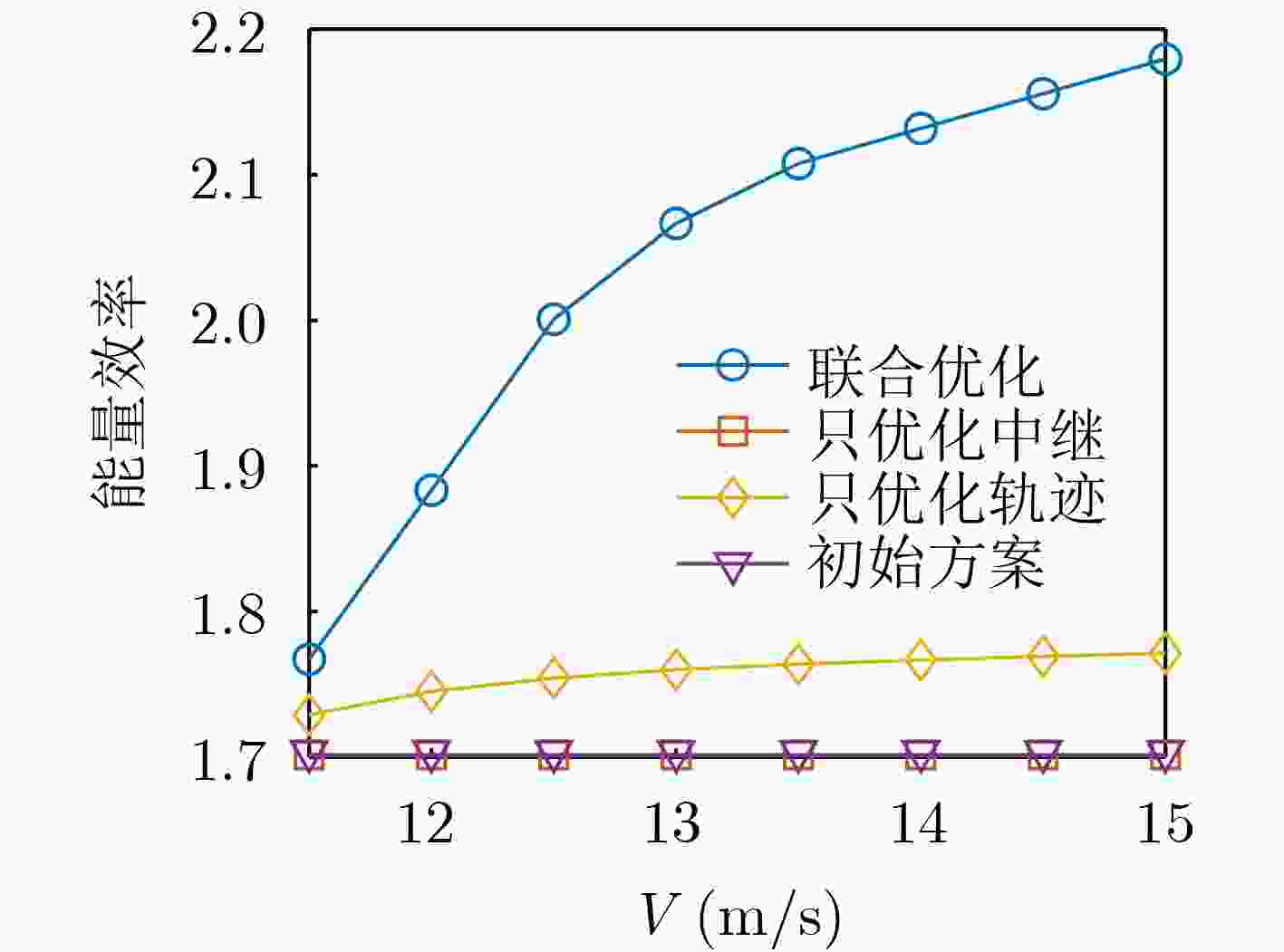
摘要: 近年来,无人机(UAVs)凭借其机动灵活的特点,广泛应用于灾后救援工作。针对灾后应急通信网络下勘察无人机执行任务的场景,为了延长应急通信网络的整体续航时间,该文考虑了中继无人机的可用通信能量以及勘察无人机的最大飞行速度和实时通信质量,通过联合优化中继选择和飞行轨迹来实现系统的能量效率最大化。对于所涉及的非确定性多项式难度(NP-hard)优化问题,该文提出一种基于连续凸近似和禁忌搜索的交替迭代算法,将原问题拆成两个子问题交替求解,得到优化问题的近似最优解。仿真结果表明,该文所提算法具有较好的收敛性,可以有效提高系统的能量效率,相比于只优化中继和只优化轨迹的基准方案,能够提升31.1%和28.2%的性能。Abstract: In recent years, Unmanned Aerial Vehicles (UAVs) have been widely used in post-disaster rescue by virtue of their mobility and flexibility. Considering the scenario that a survey UAV performs tasks using the emergency communication network, in order to extend the overall endurance of the emergency communication network, in this paper, the energy efficiency of the system is maximize by jointly optimizing the relay selection and flight trajectory of the UAV. In addition, the available communication energy of the relay UAVs as well as the maximum flight speed and real-time communication quality of the survey UAV are also considered in the optimization. The resultant Nondeterministic Polynomial hard (NP-hard) optimization problem is approximately solved using an alternate algorithm, which consists of successive convex approximation and tabu search algorithm. The alternate algorithm splits the original problem into two subproblems and solves them alternately to obtain the approximate optimal solution of the optimization problem. Simulation results show that the proposed algorithm has a desirable convergence and can significantly improve the energy efficiency of the system. The performance of the proposed algorithm is improved by 31.1% and 28.2% compared to the benchmark schemes of relay or trajectory optimization.
-
表 1 仿真参数
参数 符号 设定值 中继无人机数量 (个) M 16 时间范围 (s) T 200 时隙数量 (个) N 200 TS算法的收敛阈值 ${\varepsilon _0}$ 10–2 交替迭代算法的收敛阈值 ${\eta _0}$ 10–2 中继无人机的悬停高度 (m) H(U) 50[6] 勘察无人机的飞行高度 (m) H(S) 20[6] 中继无人机的发射功率 (dBm) pm 30[3] 勘察无人机的发射功率 (dBm) PS 27[3] 单位距离时的信道增益 (dB) ${\beta _0}$ –40[22] 中继无人机的接收噪声功率 (dBm) $\sigma _{n,m}^2$ –100 勘察无人机的接收噪声功率 (dBm) $\delta _{n,m}^2$ –100 勘察无人机的最大飞行速度 (m/s) V 13 中继无人机的可用通信能量 (J) Em 60 数据传输速率阈值 (bit/(Hz·s)) Rmin 4.6 -
[1] LIU Xiaonan, LI Zan, ZHAO Nan, et al. Transceiver design and multihop D2D for UAV IoT coverage in disasters[J]. IEEE Internet of Things Journal, 2019, 6(2): 1803–1815. doi: 10.1109/JIOT.2018.2877504 [2] AKRAM T, AWAIS M, NAQVI R, et al. Multicriteria UAV base stations placement for disaster management[J]. IEEE Systems Journal, 2020, 14(3): 3475–3482. doi: 10.1109/JSYST.2020.2970157 [3] 王博文, 孙彦景. 基于联盟图博弈的地下空间无人机应急通信网络拓扑控制算法[J]. 电子与信息学报, 2022, 44(3): 996–1005. doi: 10.11999/JEIT211205WANG Bowen and SUN Yanjing. Coalitional graph game based topology control algorithm for unmanned aerial vehicle emergency networks in underground space[J]. Journal of Electronics &Information Technology, 2022, 44(3): 996–1005. doi: 10.11999/JEIT211205 [4] WANG Jingjing, ZHU Shuang, LUO Xiangang, et al. Refined micro-scale geological disaster susceptibility evaluation based on UAV tilt photography data and weighted certainty factor method in Mountainous Area[J]. Ecotoxicology and Environmental Safety, 2020, 189: 110005. doi: 10.1016/j.ecoenv.2019.110005 [5] LIN Na, LIU Yuheng, ZHAO Liang, et al. An adaptive UAV deployment scheme for emergency networking[J]. IEEE Transactions on Wireless Communications, 2022, 21(4): 2383–2398. doi: 10.1109/TWC.2021.3111991 [6] YBAÑEZ R L, YBAÑEZ A A B, LAGMAY A M F A, et al. Imaging ground surface deformations in post-disaster settings via small UAVs[J]. Geoscience Letters, 2021, 8(1): 23. doi: 10.1186/s40562-021-00194-8 [7] MERWADAY A, TUNCER A, KUMBHAR A, et al. Improved throughput coverage in natural disasters: Unmanned aerial base stations for public-safety communications[J]. IEEE Vehicular Technology Magazine, 2016, 11(4): 53–60. doi: 10.1109/MVT.2016.2589970 [8] DO-DUY T, NGUYEN L D, DUONG T Q, et al. Joint optimisation of real-time deployment and resource allocation for UAV-aided disaster emergency communications[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(11): 3411–3424. doi: 10.1109/JSAC.2021.3088662 [9] DENG Dan and ZHOU Qingfeng. Outdated relay selection for UAV-enabled networks with cooperative NOMA[J]. Physical Communication, 2019, 32: 112–119. doi: 10.1016/j.phycom.2018.11.005 [10] LIU Dianxiong, WANG Jinlong, XU Kun, et al. Task-driven relay assignment in distributed UAV communication networks[J]. IEEE Transactions on Vehicular Technology, 2019, 68(11): 11003–11017. doi: 10.1109/TVT.2019.2942095 [11] EJAZ W, AHMED A, MUSHTAQ A, et al. Energy-efficient task scheduling and physiological assessment in disaster management using UAV-assisted networks[J]. Computer Communications, 2020, 155: 150–157. doi: 10.1016/j.comcom.2020.03.019 [12] WANG Bowen, SUN Yanjing, LIU Dianxiong, et al. Social-aware UAV-assisted mobile crowd sensing in stochastic and dynamic environments for disaster relief networks[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 1070–1074. doi: 10.1109/TVT.2019.2949634 [13] GUO Qing, PENG Jian, XU Wenzheng, et al. Minimizing the longest tour time among a fleet of UAVs for disaster area surveillance[J]. IEEE Transactions on Mobile Computing, 2022, 21(7): 2451–2465. doi: 10.1109/TMC.2020.3038156 [14] JI Jiequ, ZHU Kun, NIYATO D, et al. Joint cache placement, flight trajectory, and transmission power optimization for multi-UAV assisted wireless networks[J]. IEEE Transactions on Wireless Communications, 2020, 19(8): 5389–5403. doi: 10.1109/TWC.2020.2992926 [15] WU Qingqing, ZENG Yong, and ZHANG rui. Joint trajectory and communication design for multi-UAV enabled wireless networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(3): 2109–2121. doi: 10.1109/TWC.2017.2789293 [16] MATTINGLEY J and BOYD S. Real-time convex optimization in signal processing[J]. IEEE Signal Processing Magazine, 2010, 27(3): 50–61. doi: 10.1109/MSP.2010.936020 [17] NGUYEN N T and LEE K. Groupwise neighbor examination for Tabu search detection in large MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 1136–1140. doi: 10.1109/TVT.2019.2953635 [18] GAO Xinyu, DAI Linglong, YUEN C, et al. Turbo-like beamforming based on Tabu search algorithm for millimeter-wave massive MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7): 5731–5737. doi: 10.1109/TVT.2015.2461440 [19] POLAT O. A parallel variable neighborhood search for the vehicle routing problem with divisible deliveries and pickups[J]. Computers & Operations Research, 2017, 85: 71–86. doi: 10.1016/j.cor.2017.03.009 [20] XIA Yangkun and FU Zhuo. Improved Tabu search algorithm for the open vehicle routing problem with soft time windows and satisfaction rate[J]. Cluster Computing, 2019, 22(4): 8725–8733. doi: 10.1007/s10586-018-1957-x [21] YOU Changsheng and ZHANG Rui. Hybrid offline-online design for UAV-enabled data harvesting in probabilistic LoS channels[J]. IEEE Transactions on Wireless Communications, 2020, 19(6): 3753–3768. doi: 10.1109/TWC.2020.2978073 [22] ZENG Yong, XU Xiaoli, and ZHANG Rui. Trajectory design for completion time minimization in UAV-enabled multicasting[J]. IEEE Transactions on Wireless Communications, 2018, 17(4): 2233–2246. doi: 10.1109/TWC.2018.2790401 -





 下载:
下载:



 下载:
下载:
