Impossible Differential Cryptanalysis of Eight-Sided Fortress Based on Mixed Integer Linear Programming
-
摘要: 八阵图(ESF)是基于LBlock改进的轻量级分组密码,具有优良的软硬件实现效率。针对ESF算法的安全性,该文借助自动化搜索工具,利用不可能差分分析方法,对算法进行安全性评估。首先结合ESF的结构特性和$ S $盒的差分传播特性,建立了基于混合整数线性规划(MILP)的不可能差分搜索模型;其次利用算法 $ S $盒的差分传播特性和密钥扩展算法中轮子密钥间的相互关系,基于一条9轮不可能差分区分器,通过向前扩展2轮向后扩展4轮,实现了对ESF算法的15轮密钥恢复攻击。分析结果表明,该攻击的数据复杂度和时间复杂度分别为$ {2^{60.16}} $和 $ {2^{67.44}} $,均得到有效降低,且足够抵抗不可能差分分析。
-
关键词:
- 八阵图(ESF) /
- 不可能差分分析 /
- 混合整数线性规划(MILP)
Abstract: Eight-Sided Fortress(ESF), an improved lightweight block cipher based on LBlock, has excellent software and hardware implementation efficiency. For the security of ESF, with the help of automated search tools, the algorithm is evaluated for security using the impossible differential cryptanalysis. Firstly, an impossible differential search model based on Mixed Integer Linear Programming (MILP) is built by combining the structure of ESF algorithm and the differential propagation of $ S $-box. Secondly, based on a 9-round impossible differential distinguisher of ESF, using the differential propagation characteristics of the $ S $-box and the relationship of the round subkeys in the key schedule, a 15-round-attack is presented to ESF by adding two rounds in the front and adding four rounds in the end. It is found that the data complexity of plaintexts and time complexity of encryptions of the attack need are $ {2^{60.16}} $ and $ {2^{67.44}} $, respectively. The results show that the data complexity and time complexity have been effectively reduced, and the proposed method is able to resist impossible differential cryptanalysis. -
表 1 ESF的S盒
$ \boldsymbol{x} $ 0 1 2 3 4 5 6 7 8 9 a b c d e f $ {S_0} $ 3 8 f 1 a 6 5 b e d 4 2 7 0 9 c $ {S_1} $ f c 2 7 9 0 5 a 1 b e 8 6 d 3 4 $ {S_2} $ 8 6 7 9 3 c a f d 1 e 4 0 b 5 2 $ {S_3} $ 0 f b 8 c 9 6 3 d 1 2 4 a 7 5 e $ {S_4} $ 1 f 8 3 c 0 b 6 2 5 4 a 9 e 7 d $ {S_5} $ f 5 2 b 4 a 9 c 0 3 e 8 d 6 7 1 $ {S_6} $ 7 2 c 5 8 4 6 b e 9 1 f d 3 a 0 $ {S_7} $ 1 d f 0 e 8 2 b 7 4 c a 9 3 5 6 表 2 ESF 的S0盒差分分布表
0 1 2 3 4 5 6 7 8 9 a b c d e f 0 16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 2 0 2 2 2 0 0 0 2 2 0 4 0 2 0 0 0 0 0 0 0 0 0 2 2 0 4 2 2 4 3 0 2 2 2 0 0 0 2 0 4 0 2 2 0 0 0 4 0 0 0 0 0 0 0 0 0 4 4 0 0 4 4 0 5 0 0 2 0 4 2 0 0 2 0 2 2 0 0 2 0 6 0 2 2 4 0 2 2 4 0 0 0 0 0 0 0 0 7 0 0 2 0 4 2 0 0 2 2 0 2 0 2 0 0 8 0 0 0 2 0 2 2 2 0 0 0 2 2 4 0 0 9 0 2 2 0 0 2 2 0 0 2 2 0 0 2 2 0 a 0 2 2 2 0 0 0 2 0 0 4 2 2 0 0 0 b 0 2 2 0 0 2 2 0 0 0 0 0 4 0 0 4 c 0 2 0 0 4 0 2 0 2 2 0 2 0 2 0 0 d 0 0 0 4 0 0 0 4 4 0 0 0 0 0 0 4 e 0 2 0 0 4 0 2 0 2 0 2 2 0 0 2 0 f 0 2 2 0 0 2 2 0 4 0 0 0 0 0 0 4 表 3 ESF的S盒差分传播特性
$ {S_0} $ $ {S_1} $ $ {S_2} $ $ {S_4} $ $ {S_5} $ $ {S_6} $ $ \alpha $ $ \beta $ $ \alpha $ $ \beta $ $ \alpha $ $ \beta $ $ \alpha $ $ \beta $ $ \alpha $ $ \beta $ $ \alpha $ $ \beta $ 0010 $ 1 * * * $ 0100 $ * 1 * * $ 0010 $ * * * 1 $ 0100 $ * * * 1 $ 0100 $ * * * 1 $ 0010 $ * * 1 * $ 0100 $ 1 * * * $ 1000 $ * 1 * * $ 1000 $ * * * 1 $ 1011 $ * * * 1 $ 1011 $ * * * 1 $ 0100 $ * * 1 * $ 0110 $ 0 * * * $ 1100 $ * 0 * * $ 1010 $ * * * 0 $ 1111 $ * * * 0 $ 1111 $ * * * 0 $ 0110 $ * * 0 * $ 表 4 ESF的S盒差分概率传播特性
$ S $ $ {S_0} $ $ {S_6} $ $ \alpha $ $ 1000 $ $ 0001 $ $ \beta $ $ * * * * $ $ * * * * $ $ P $ $\dfrac{1}{8}$ $\dfrac{1}{8}$ 算法1 搜索 ESF 算法加密方向的有效差分路径 输入: 64 bit的明文输入差分$ \Delta X $, 输出:加密后的输出差分集合$ {\text{List}}{\text{.}} $ 1. $ {\text{set}} = \{ \Delta X\} $; 2. 如果$ {\text{set}} $中包含部分比特已知的差分; 3. for $ \Delta X $ in $ {\text{set}} $ 2. $ {\text{List}}{\text{.append(}}\Delta X{\text{)}} $; 4. $ \Delta {x_0} - \Delta {x_1} - \Delta {x_2} + \Delta {x_3} - \Delta {y_0} + 2 \ge 0 $; #当$ {\alpha _0} = 0110, $ $ {\beta _0} = 0 * * * * $时的不等式约束,对于其他$ S $盒有类似性质 5. $\Delta {r_1}{\text{ + } }\Delta { {\text{k} }_1} + \Delta {m_1} - 2d \ge 0,{{ d} } \ge \varDelta {r_1},{{ d} } \ge \varDelta { {\text{k} }_1},{{ d} } \ge \varDelta {m_1},{\text{ } }\varDelta {r_1}{\text{ + } }\varDelta { {\text{k} }_1} + \varDelta {m_1} \le 2$; #异或的约束条件
6. $\displaystyle\sum\limits_{i = 0}^3 {\Delta {x_i} - 4A \le 0,} {\text{ } }\displaystyle\sum\limits_{i = 0}^3 {\Delta {x_i} - A \ge 0,} {\text{ 4} }\displaystyle\sum\limits_{i = 0}^3 {\Delta {y_i} - \displaystyle\sum\limits_{i = 0}^3 {\Delta {x_i} \ge 0,} {\text{ } } } {\text{ 4} }\displaystyle\sum\limits_{i = 0}^3 {\Delta {x_i} - \displaystyle\sum\limits_{i = 0}^3 {\Delta {y_i} \ge 0} {\text{ } } }$; #$ S $盒约束条件7. $ S $盒差分传播特性得到的213个不等式约束条件; 8. 利用GUROBI求解MILP模型,判断是否存在可行解; 9. 若存在可行解,则输出$ {\text{set}}{\text{.append}} $(满足上述条件的输出差分$ \Delta Y $); 10. ${\text{set = set } }-\left( {\Delta X} \right)$,重复执行上述步骤1-步骤9,直到$ {\text{set}} $全为未知的比特; 11. return List. 算法2 寻找最长不可能差分区分器轮数 输入: 加密后的差分路径集合$ {\text{E}}{\text{.List}} $, 解密后的差分路径集合
$ {\text{D}}{\text{.List}} $输出:输出最长不可能差分区分器轮数 1. $ r = 0 $; 2. for $ i $ in range len($ {\text{E}}{\text{.List}} $) 3. for $ j $ in range len($ {\text{D}}{\text{.List}} $) 4. if ${\text{E} }{{.{\rm{List}}[i]} } \ne {\text{D} }{{.{\rm{List}}[j]} }$; 5. if $ r > i + j $ 6. $ r = r $; 7. else 8. $ r = i + j $; 9. return $ r. $ 表 5 ESF 分析方法结果对比
攻击轮数 分析方法 时间复杂度 数据复杂度 文献 11 不可能差分分析 $ {2^{75.5}} $ $ {2^{59}} $ 文献[10] 11 不可能差分分析 $ {2^{32}} $ $ {2^{53}} $ 文献[11] 12 不可能差分分析 $ {2^{60.45}} $ $ {2^{53}} $ 文献[12] 13 截断不可能差分分析 $ {2^{61.99}} $ $ {2^{77.39}} $ 文献[14] 14 相关密钥不可能差分分析 $ {2^{43.95}} $ $ {2^{62}} $ 文献[13] 15 不可能差分分析 $ {2^{70.02}} $ $ {2^{64.3}} $ 文献[16] 15 不可能差分分析 $ {2^{67.44}} $ $ {2^{60.16}} $ 本文 -
[1] BOGDANOV A, KNUDSEN L R, LEANDER G, et al. PRESENT: An ultra-lightweight block cipher[C]. Proceedings of the 9th International Workshop on Cryptographic Hardware and Embedded Systems-CHES 2007, Vienna, Austria, 2007: 450–466. [2] WU Wenling and ZHANG Lei. LBlock: A lightweight block cipher[C]. Proceedings of the 9th International Conference on Applied Cryptography and Network Security, Nerja, Spain, 2011: 327–344. [3] BANIK S, BAO Zhenzhen, ISOBE T, et al. WARP: Revisiting GFN for lightweight 128-bit block cipher[C]. Proceedings of the 27th International Conference on Selected Areas in Cryptography, Halifax, Canada, 2021: 535–564. [4] 曹梅春, 张文英, 陈彦琴, 等. RAIN: 一种面向软硬件和门限实现的轻量分组密码算法[J]. 计算机研究与发展, 2021, 58(5): 1045–1055. doi: 10.7544/issn1000-1239.2021.20200933CAO Meichun, ZHANG Wenying, CHEN Yanqin, et al. RAIN: A lightweight block cipher towards software, hardware and threshold implementations[J]. Journal of Computer Research and Development, 2021, 58(5): 1045–1055. doi: 10.7544/issn1000-1239.2021.20200933 [5] DAS A K, KAR N, DEB S, et al. bFLEX-γ: A lightweight block cipher utilizing key cross approach via probability density function[J]. Arabian Journal for Science and Engineering, 2022, 47(8): 10563–10578. doi: 10.1007/s13369-022-06651-6 [6] LIU Xuan, ZHANG Wenying, LIU Xiangzhong, et al. Eight-sided fortress: A lightweight block cipher[J]. The Journal of China Universities of Posts and Telecommunications, 2014, 21(1): 104–108,128. doi: 10.1016/S1005-8885(14)60275-2 [7] 吴文玲, 张蕾. 不可能差分密码分析研究进展[J]. 系统科学与数学, 2008, 28(8): 971–983. doi: 10.12341/jssms10197WU Wenling and ZHANG Lei. The state-of-the-art of research on impossible differential cryptanalysis[J]. Journal of Systems Science and Mathematical Sciences, 2008, 28(8): 971–983. doi: 10.12341/jssms10197 [8] 韦永壮, 史佳利, 李灵琛. LiCi分组密码算法的不可能差分分析[J]. 电子与信息学报, 2019, 41(7): 1610–1617. doi: 10.11999/JEIT180729WEI Yongzhuang, SHI Jiali, and LI Lingchen. Impossible differential cryptanalysis of LiCi block cipher[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1610–1617. doi: 10.11999/JEIT180729 [9] 任炯炯, 侯泽洲, 李曼曼, 等. 改进的减轮MIBS-80密码的中间相遇攻击[J]. 电子与信息学报, 2022, 44(8): 2914–2923. doi: 10.11999/JEIT210441REN Jiongjiong, HOU Zezhou, LI Manman, et al. Improved meet-in-the-middle attacks on reduced-round MIBS-80 Cipher[J]. Journal of Electronics &Information Technology, 2022, 44(8): 2914–2923. doi: 10.11999/JEIT210441 [10] 刘宣, 刘枫, 孟帅. 轻量级分组密码算法ESF的不可能差分分析[J]. 计算机工程与科学, 2013, 35(9): 89–93. doi: 10.3969/j.issn.1007-130X.2013.09.014LIU Xuan, LIU Feng, and MENG Shuai. Impossible differential cryptanalysis of lightweight block cipher ESF[J]. Computer Engineering &Science, 2013, 35(9): 89–93. doi: 10.3969/j.issn.1007-130X.2013.09.014 [11] 陈玉磊, 卫宏儒. ESF算法的不可能差分密码分析[J]. 计算机科学, 2016, 43(8): 89–91,99. doi: 10.11896/j.issn.1002-137X.2016.08.018CHEN Yulei and WEI Hongru. Impossible differential cryptanalysis of ESF[J]. Computer Science, 2016, 43(8): 89–91,99. doi: 10.11896/j.issn.1002-137X.2016.08.018 [12] 高红杰, 卫宏儒. 用不可能差分法分析12轮ESF算法[J]. 计算机科学, 2017, 44(10): 147–149,181. doi: 10.11896/j.issn.1002-137X.2017.10.028GAO Hongjie and WEI Hongru. Impossible differential attack on 12-round block cipher ESF[J]. Computer Science, 2017, 44(10): 147–149,181. doi: 10.11896/j.issn.1002-137X.2017.10.028 [13] 谢敏, 杨盼. ESF算法的相关密钥不可能差分分析[J]. 计算机工程与科学, 2018, 40(7): 1199–1205. doi: 10.3969/j.issn.1007-130X.2018.07.008XIE Min and YANG Pan. Related-key impossible differential cryptanalysis on ESF[J]. Computer Engineering &Science, 2018, 40(7): 1199–1205. doi: 10.3969/j.issn.1007-130X.2018.07.008 [14] 李明明, 郭建胜, 崔竞一, 等. ESF算法的截断不可能差分分析[J]. 密码学报, 2019, 6(5): 585–593. doi: 10.13868/j.cnki.jcr.000324LI Mingming, GUO Jiansheng, CUI Jingyi, et al. Truncated impossible difference cryptanalysis of ESF[J]. Journal of Cryptologic Research, 2019, 6(5): 585–593. doi: 10.13868/j.cnki.jcr.000324 [15] LI Jun, WANG Hongyan, QIU Xueying, et al. Integral analysis of GRANULE and ESF block ciphers based on MILP[C]. Proceedings of 2021 12th International Conference on Information and Communication Systems (ICICS), Valencia, Spain, 2021: 10–16. [16] WU Xiaonian, YAN Jiaxu, LI Lingchen, et al. Impossible differential cryptanalysis on ESF algorithm with simplified MILP model[J]. KSII Transactions on Internet and Information Systems, 2021, 15(10): 3815–3833. doi: 10.3837/tiis.2021.10.018 [17] 武小年, 李迎新, 韦永壮, 等. GRANULE和MANTRA算法的不可能差分区分器分析[J]. 通信学报, 2020, 41(1): 94–101. doi: 10.11959/j.issn.1000-436x.2020025WU Xiaonian, LI Yingxin, WEI Yongzhuang, et al. Impossible differential distinguisher analysis of GRANULE and MANTRA algorithm[J]. Journal on Communications, 2020, 41(1): 94–101. doi: 10.11959/j.issn.1000-436x.2020025 [18] TEZCAN C. Improbable differential attacks on PRESENT using undisturbed bits[J]. Journal of Computational and Applied Mathematics, 2014, 259: 503–511. doi: 10.1016/j.cam.2013.06.023 -





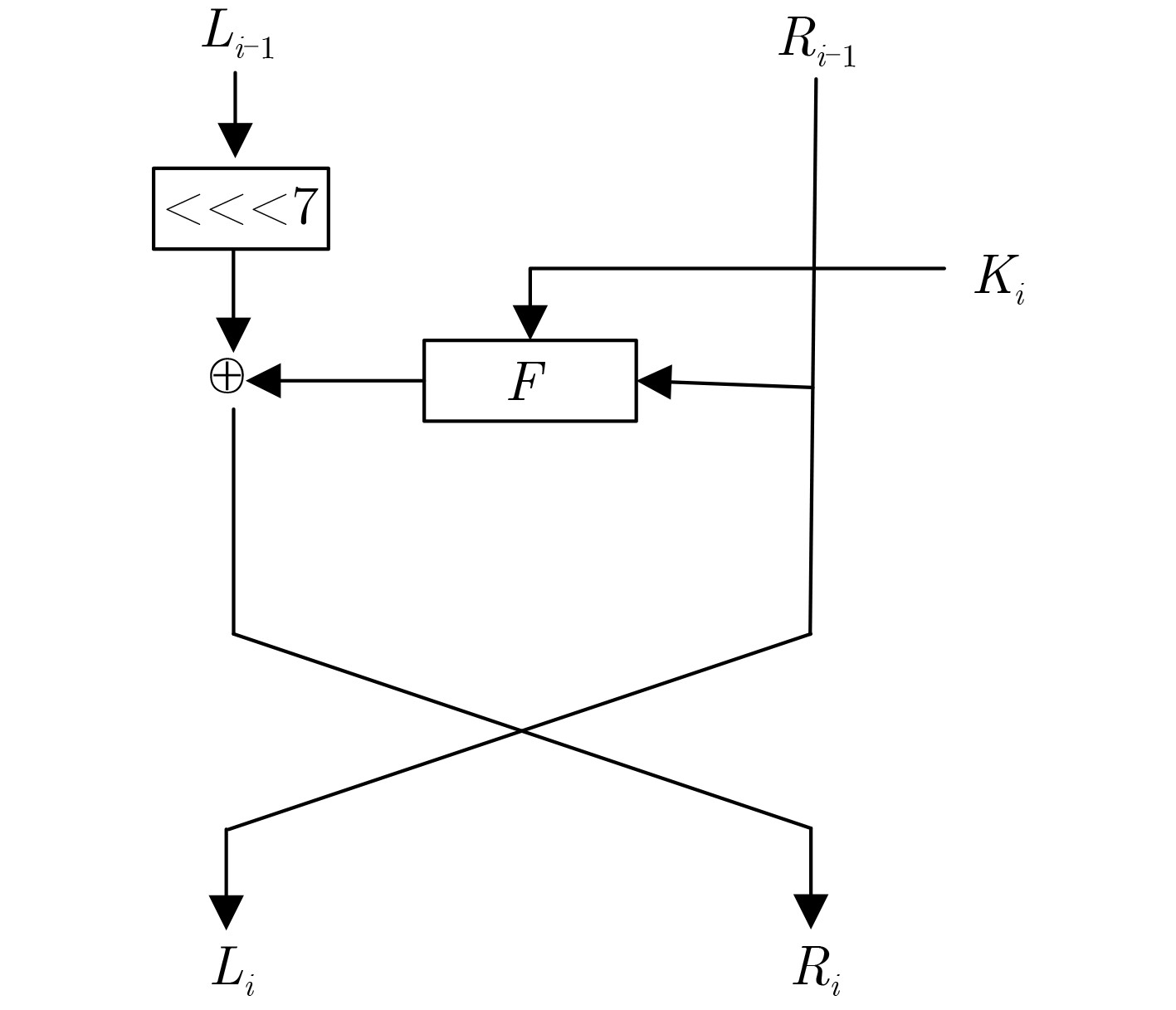
 下载:
下载:

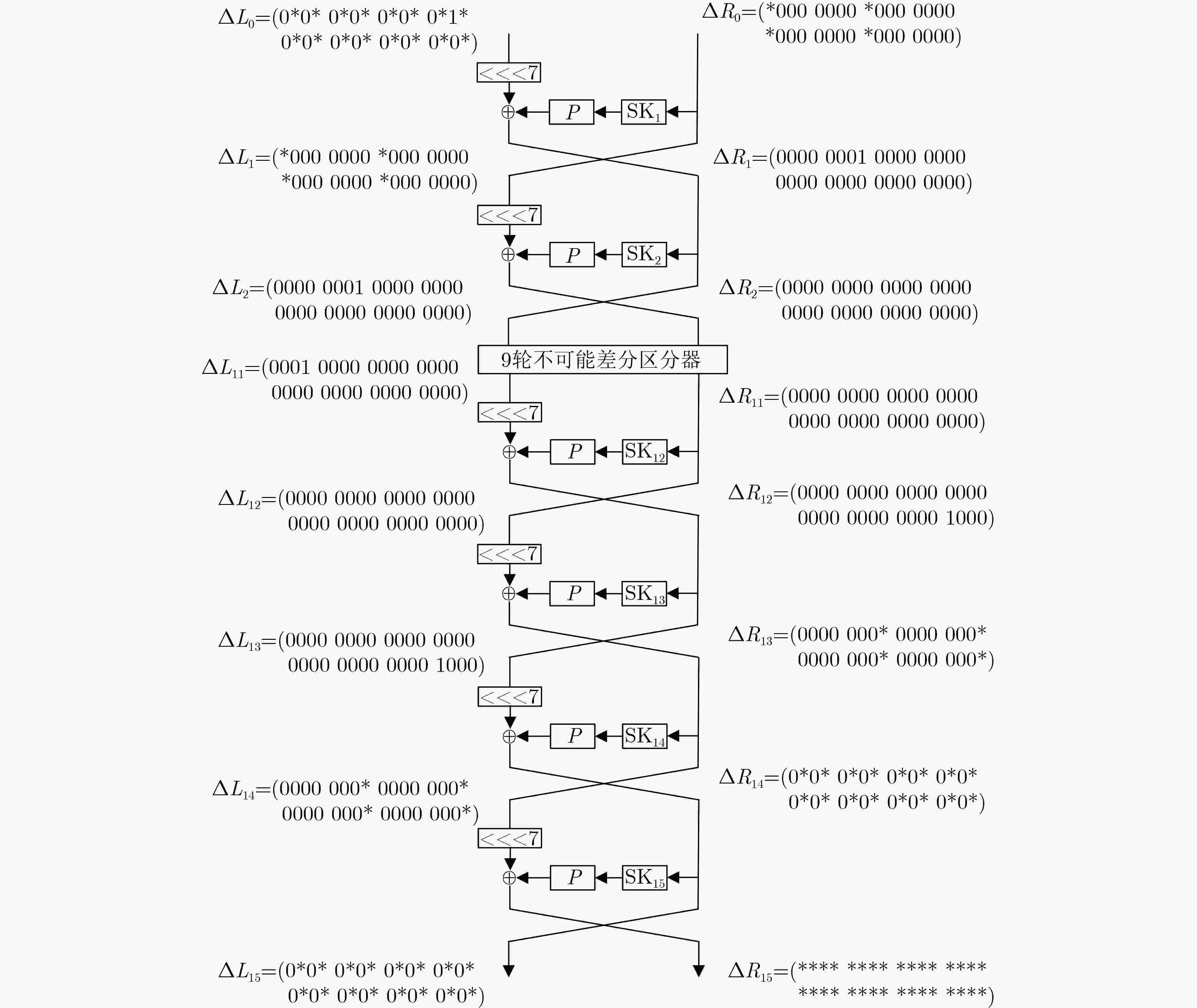


 下载:
下载:
