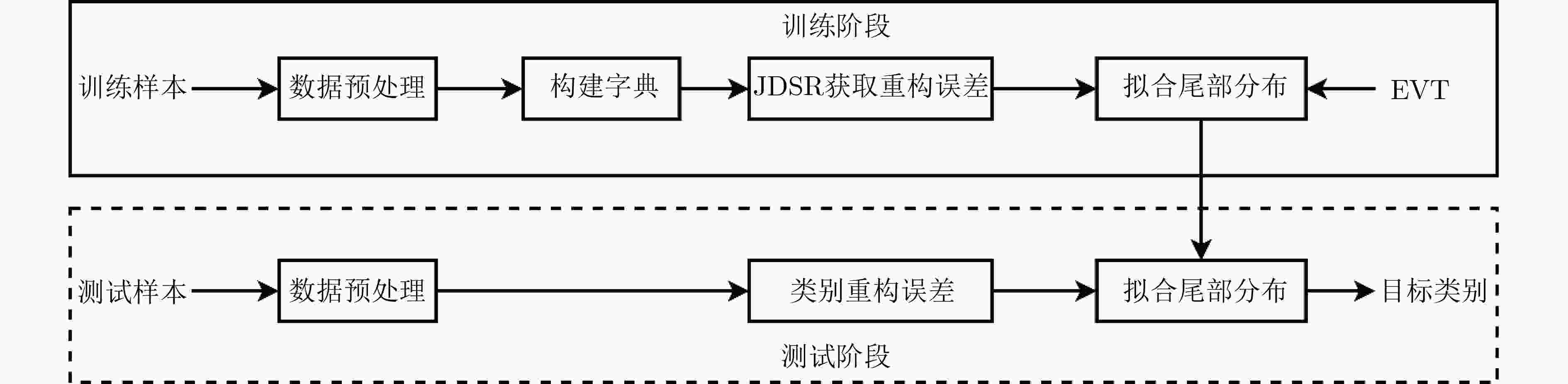
Open-set HRRP Target Recognition Method Based on Joint Dynamic Sparse Representation
-
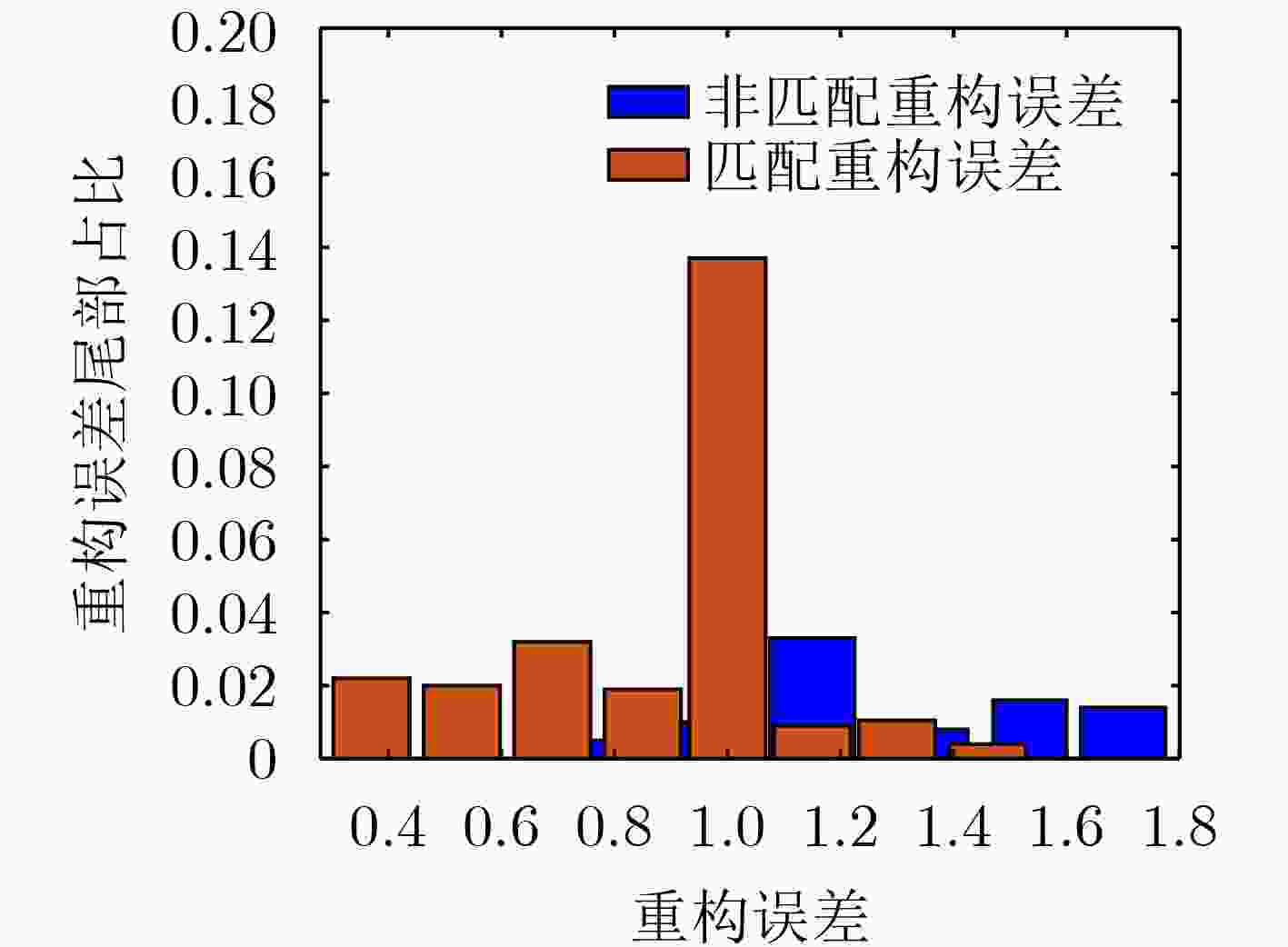
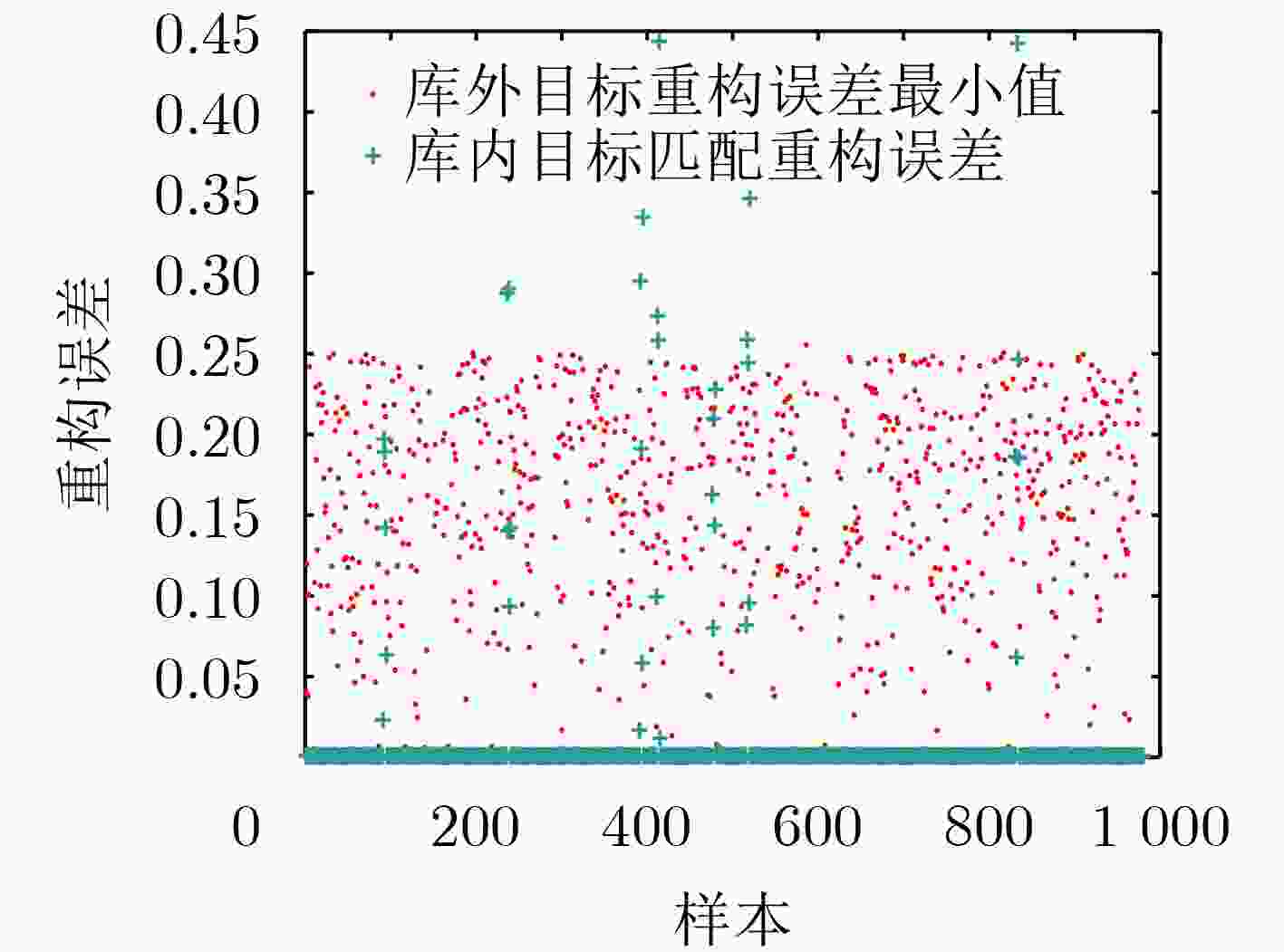
摘要: 针对开集条件下多视高分辨距离像(HRRP)目标识别问题,提出了一种基于联合动态稀疏表示(JDSR)的开集识别方法。该方法利用JDSR求解多视HRRP在过完备字典上的重构误差,采用极值理论(EVT)对匹配和非匹配类别的重构误差拖尾进行建模,将开集识别问题转化为假设检验问题求解。识别时利用重构误差确定候选类,根据尾部分布的置信度获得匹配类与非匹配类得分,并将两者的加权和作为类别判据最终确定库外目标或候选类。该方法能够有效利用多视观测来自相同目标的先验信息提高开集条件下的HRRP识别性能,并且对多视数据不同的获取场景具有良好的适应性。利用从MSTAR反演生成的HRRP数据对算法进行了测试,结果表明所提方法的性能优于主流开集识别方法。Abstract: Focusing on the issue of multi-view High-Resolution Range Profile (HRRP) target recognition in an open set, a novel method based on Joint Dynamic Sparse Representation (JDSR) is presented. First, JDSR is used to solve the reconstruction error of multi-view HRRP on the over completed dictionary. The reconstruction error trails of matched and unmatched categories are modeled using Extreme Value Theory (EVT), and subsequently, the open-set recognition problem is transformed into a hypothesis test problem. The reconstruction error is used to determine candidate classes during the identification phase. The matched and nonmatched class scores are obtained based on the confidence level of the tail distribution, and their weighted sum is used to decide whether the inputs are from nonlibrary categories or candidate classes. The input HRRPs are obtained from the same target and can be used as useful information to improve recognition performance. The proposed method can effectively use such prior information for performance enhancement under the open-set condition. Moreover, performance can remain robust under multiview data acquisition scenarios. The HRRP data generated from MSTAR chips are used for the identification experiments, and the results reveal that the proposed method performs considerably better than some state-of-the-art methods.
-
算法1 重构误差拟合及参数估计流程 1. 输入:训练阶段重构误差${\boldsymbol{R}} = \left[ {{R_1},{R_2},\cdots,{R_c}} \right]$ 2. 匹配类重构误差${\boldsymbol{R}}_c^m = {\boldsymbol{R}}\left( {:,c} \right)$,非匹配类重构误差:${\boldsymbol{R}}_c^{nm} = \displaystyle\sum\nolimits_{i:i \ne c} {R\left( {:,i} \right)} $ 3. 对重构误差排序:${{\boldsymbol{R}}_c} = {\left[ {{r_{c1}},{r_{c2}}, \cdots ,{r_{c{N_c}}}} \right]^{\rm{T}}},{r_{c1}} \le {r_{c2}} \le \cdots \le {r_{c{N_c}}}$ 4. 选取匹配类重构误差右拖尾$ {\boldsymbol{\rho}} _c^m = \left[ {r_{c\left( {{N_c}\rho } \right)}^m,r_{c\left( {{N_c}\rho + 1} \right)}^m, \cdots ,r_{c{N_c}}^m} \right] $,非匹配类重构误差左拖尾$ {\boldsymbol{\rho}} _c^{nm} = \left[ {r_{c1}^{nm},r_{c2}^{nm}, \cdots ,r_{c\left( {{N_c}\rho } \right)}^{nm}} \right] $ 5. 选取匹配类门限值$t_c^m = r_{c({N_c}\rho - 1)}^m$,非匹配类门限值$t_c^{nm} = r_{c({N_c}\rho + 1)}^{nm}$ 6. 匹配类溢额值$ {\boldsymbol{X}}_c^m = \left[ {r_{c\left( {{N_c}\rho } \right)}^m - t_c^m,r_{c\left( {{N_c}\rho + 1} \right)}^m - t_c^m, \cdots ,r_{c{N_c}}^m - t_c^m} \right] $,非匹配类溢额值
$ {\boldsymbol{X}}_c^{nm} = - \left[ {r_{c1}^{nm} - t_c^{nm},r_{c2}^{nm} - t_c^{nm}, \cdots ,r_{c\left( {{N_c}\rho } \right)}^{nm} - t_c^{nm}} \right] $7. 估计极值参数$\lg L\left( {{\sigma ^m},{\gamma ^m}} \right) = - {N_c}\lg \sigma - \left( {\dfrac{1}{\gamma } + 1} \right)\displaystyle\sum\nolimits_{i = 1}^{{N_c}} {\lg \left( {1 + \gamma \frac{{X_c^m}}{\sigma }} \right)} $,
$\lg L\left( {{\sigma ^{nm}},{\gamma ^{nm}}} \right) = - {N_c}\lg \sigma - \left( {\dfrac{1}{\gamma } + 1} \right)\displaystyle\sum\nolimits_{i = 1}^{{N_c}} {\lg \left( {1 + \gamma \frac{{X_c^{nm}}}{\sigma }} \right)} $8. 输出参数${\hat \sigma ^m},{\hat \gamma ^m},{\hat \sigma ^{nm}},{\hat \gamma ^{nm}}$ 算法2 JDSR-OSR训练算法 1 输入:训练样本$ {{\boldsymbol{Y}}_{{\rm{tr}}}} = [{{\boldsymbol{Y}}_1},{{\boldsymbol{Y}}_2}, \cdots ,{{\boldsymbol{Y}}_C}] $,标签集
${L_{{\rm{tr}}}} = [{L_1},{L_2}, \cdots ,{L_C}]$,字典矩阵${\boldsymbol{D}}$,稀疏度K,多视数目n,
尾部大小$\rho $2 训练样本划分为多视数据${{\boldsymbol{Y}}_{11}} = \left[ {{{\boldsymbol{y}}_{11}},{{\boldsymbol{y}}_{12}}, \cdots ,{{\boldsymbol{y}}_{1(1 + n)}}} \right] $,
${L_{11}} = \left[ {{l_1},{l_{12}}, \cdots ,{l_{1(1 + n)}}} \right]$, ···,
$ {{\boldsymbol{Y}}_{ci}} = \left[ {{{\boldsymbol{y}}_{ci}},{{\boldsymbol{y}}_{c(i + 1)}}, \cdots ,{{\boldsymbol{y}}_{c(i + n)}}} \right] $,
Lci=[lci, lc(i +1), ··· , lc(i +n)]3 计算重构误差$ R \leftarrow {\rm{JDSR}}\left( {{\boldsymbol{Y}},l,{\boldsymbol{D}},K} \right) $ 4 匹配类重构误差:$R_c^m = R\left( {:,c} \right)$;非匹配类重构误差:
$R_c^{nm} = \displaystyle\sum\limits_{i:i \ne c} {R\left( {:,i} \right)} $5 拟合尾部极值参数:${\text{GPDfit}}\left( {R_c^m,\rho } \right) \to \hat \sigma _c^m,\hat \gamma _c^m$
${\text{GPDfit}}\left( { - R_c^{nm},\rho } \right) \to \hat \sigma _c^{nm},\hat \gamma _c^{nm}$6 输出极值参数 $\hat \sigma _c^m,\hat \gamma _c^m,\hat \sigma _c^{nm},\hat \gamma _c^{nm}$ 算法3 JDSR-OSR分类方法 1 输入:多视数据${{\boldsymbol{Y}}_j}$, ${\boldsymbol{D}}$, $k$, ${\hat \sigma ^m},{\hat \gamma ^m},{\hat \sigma ^{nm}},{\hat \gamma ^{nm}}$, ${\delta _g}$, $w$ 2 计算重构误差$R \leftarrow {\text{JDSR}}\left( {{{\boldsymbol{Y}}_j},{\boldsymbol{D}},K} \right)$ 3 得到候选类别${c^ * } = \mathop {\arg \min }\limits_i {R_i}$ 4 ${r^m} = R_{{c^ * }}^m,{r^{nm}} = \displaystyle\sum\limits_{i \ne {c^ * }} {{R_i}} $ 5 $\begin{gathered} {{\rm{score}}_m} = G\left( {{r^m};{{\hat \sigma }^m}\left( {{c^ * }} \right),{{\hat \gamma }^m}\left( {{c^ * }} \right)} \right), \\ {{\rm{score}}_{nm}} = G\left( {{r^{nm}};{{\hat \sigma }^{nm}}\left( {{c^ * }} \right),{{\hat \gamma }^{nm}}\left( {{c^ * }} \right)} \right) \\ \end{gathered} $ 6 ${\rm{score}} = {{\rm{score}}_m} + w \cdot {{\rm{score}}_{nm}}$
$\begin{gathered} \begin{array}{*{20}{c}} {{\text{if}}}&{{\rm{score}} > {\delta _g}} \end{array} \\ \begin{array}{*{20}{c}} {}&{{{\boldsymbol{Y}}_j} \in {\text{openset}}} \end{array} \\ \quad {\text{else}} \\ \begin{array}{*{20}{c}} {}&{{\text{Clas}}{{\text{s}}_{{{\boldsymbol{Y}}_j}}} = {c^ * }} \end{array} \\ \end{gathered} $7 输出${{\boldsymbol{Y}}_j}$类别 表 1 Situation-Ⅰ JDSR-OSR的混淆矩阵
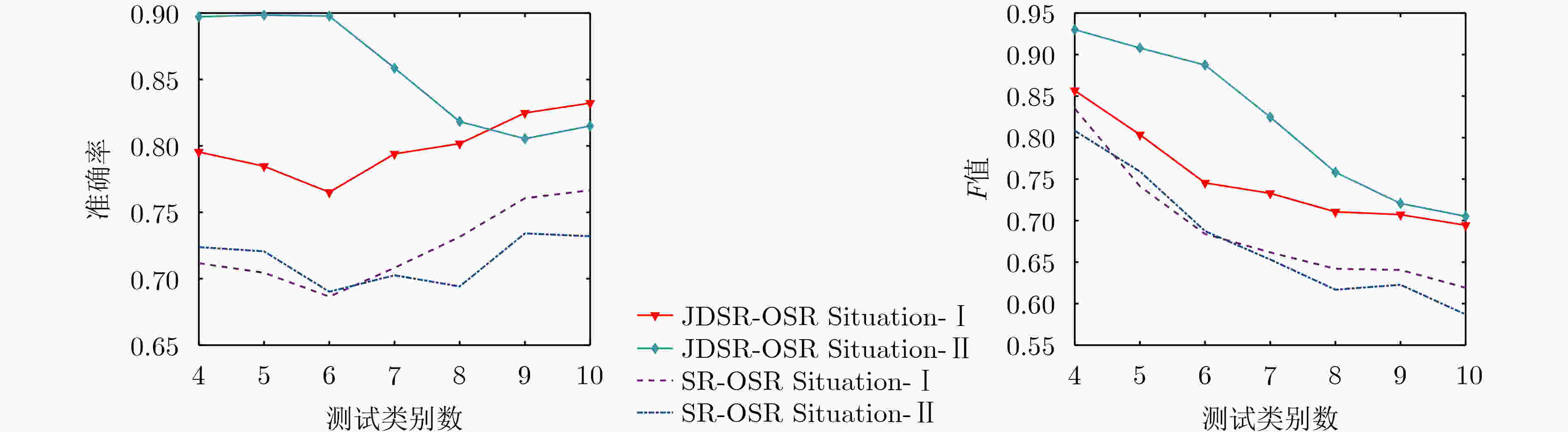
类别 BMP2 BTR70 T72 未知新类 BMP2 0.712 0.088 0.060 0.140 BTR70 0.066 0.827 0.025 0.082 T72 0.030 0.007 0.825 0.138 BTR60 0.048 0.124 0.027 0.801 2S1 0.045 0.086 0.131 0.738 BRDM2 0.134 0.076 0.038 0.752 D7 0.011 0.010 0.080 0.899 T62 0.003 0 0.121 0.876 ZIL 0 0 0.051 0.949 ZSU 0 0 0.096 0.904 表 2 Situation-Ⅱ JDSR-OSR的混淆矩阵
类别 BMP2 BTR70 T72 未知新类 BMP2 0.735 0.056 0.019 0.190 BTR70 0.020 0.910 0.022 0.048 T72 0.005 0 0.960 0.035 BTR60 0.019 0.042 0.039 0.900 2S1 0.016 0.056 0.045 0.883 BRDM2 0.066 0.018 0 0.916 D7 0 0.002 0.247 0.751 T62 0 0 0.403 0.597 ZIL 0 0 0.177 0.823 ZSU 0 0 0.318 0.682 表 3 JDSR-OSR与其他方法平均识别率的对比结果
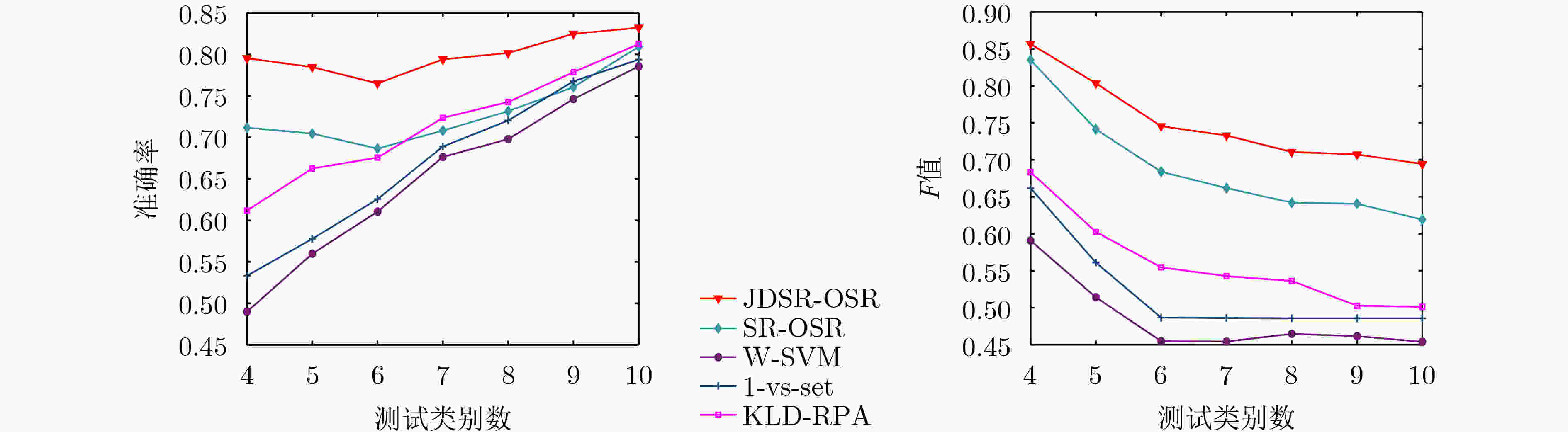
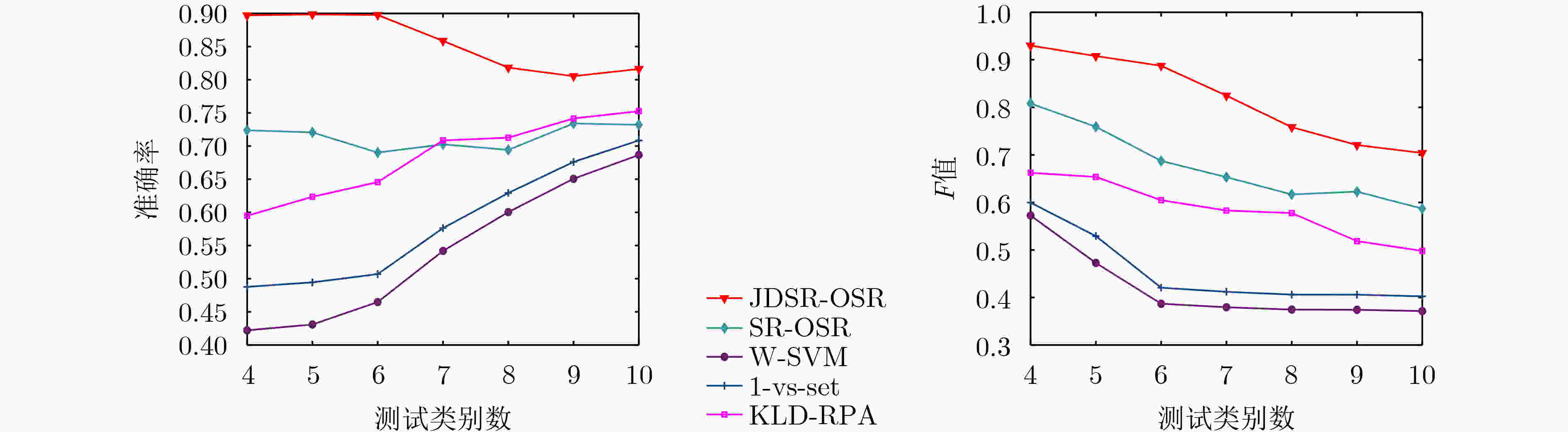
方法 Situation-Ⅰ Situation-Ⅱ JDSR-OSR 0.832 0.816 SR-OSR 0.809 0.732 W-SVM 0.786 0.687 1-vs-set 0.794 0.709 KLD-RPA 0.813 0.752 表 4 不同测试类别下的算法运行时间对比(s)
测试类别数 SR-OSR JDSR-OSR 4 16.585 15.637 5 18.875 18.400 6 19.765 20.937 7 22.520 23.584 8 24.150 26.731 9 25.640 29.815 10 30.015 032.076 -
[1] 付哲泉, 李尚生, 李相平, 等. 基于高效可扩展改进残差结构神经网络的舰船目标识别技术[J]. 电子与信息学报, 2020, 42(12): 3005–3012. doi: 10.11999/JEIT190913.FU Zhequan, LI Shangsheng, LI Xiangping, et al. Ship target recognition based on highly efficient scalable improved residual structure neural network[J]. Journal of Electronics & Information Technology, 2020, 42(12): 3005–3012. doi: 10.11999/JEIT190913. [2] 贺丰收, 何友, 刘准钆, 等. 卷积神经网络在雷达自动目标识别中的研究进展[J]. 电子与信息学报, 2020, 42(1): 119–131. doi: 10.11999/JEIT180899.HE Fengshou, HE You, LIU Zhunga, et al. Research and development on applications of convolutional neural networks of radar automatic target recognition[J]. Journal of Electronics & Information Technology, 2020, 42(1): 119–131. doi: 10.11999/JEIT180899. [3] GÖRNITZ N, LIMA L A, MÜLLER K R, et al. Support vector data descriptions and k-means clustering: One class?[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(9): 3994–4006. doi: 10.1109/TNNLS.2017.2737941. [4] PÉREZ G J, SANTIBÁÑEZ M, VALDOVINOS R M, et al. On-line learning with reject option[J]. IEEE Latin America Transactions, 2018, 16(1): 279–286. doi: 10.1109/TLA.2018.8291485. [5] GEIFMAN Y and EL-YANIV R. Selective classification for deep neural networks[C]. Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 4885–4894. [6] SCHEIRER W J, DE REZENDE ROCHA A, SAPKOTA A, et al. Toward open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(7): 1757–1772. doi: 10.1109/TPAMI.2012.256. [7] SCHEIRER W J, JAIN L P, and BOULT T E. Probability models for open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(11): 2317–2324. doi: 10.1109/TPAMI.2014.2321392. [8] JAIN L P, SCHEIRER W J, and BOULT T E. Multi-class open set recognition using probability of inclusion[C]. Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 2014: 393–409. doi: 10.1007/978-3-319-10578-9_26. [9] ZHANG He and PATEL V M. Sparse representation-based open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1690–1696. doi: 10.1109/TPAMI.2016.2613924. [10] BENDALE A and BOULT T. Towards open world recognition[C]. Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 1893–1902. doi: 10.1109/CVPR.2015.7298799. [11] SADHUKHAN P. Can reverse nearest neighbors perceive unknowns?[J]. IEEE Access, 2020, 8: 6316–6343. doi: 10.1109/ACCESS.2019.2963471. [12] SHU Lei, XU Hu, and LIU Bing. DOC: Deep open classification of text documents[C]. Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 2017: 2911–2916. doi: 10.18653/v1/D17-1314. [13] OZA P and PATEL V M. C2AE: Class conditioned auto-encoder for open-set recognition[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, USA, 2019: 2302–2311. doi: 10.1109/CVPR.2019.00241. [14] ZENG Zhiqiang, SUN Jinping, XU Congan, et al. Unknown SAR target identification method based on feature extraction network and KLD–RPA joint discrimination[J]. Remote Sensing, 2021, 13(15): 2901. doi: 10.3390/rs13152901. [15] RUDD E M, JAIN L P, SCHEIRER W J, et al. The extreme value machine[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(3): 762–768. doi: 10.1109/TPAMI.2017.2707495. [16] PAPPADÀ R, PERRONE E, DURANTE F, et al. Spin-off extreme value and Archimedean copulas for estimating the bivariate structural risk[J]. Stochastic Environmental Research and Risk Assessment, 2016, 30(1): 327–342. doi: 10.1007/s00477-015-1103-8. [17] FALK M and STUPFLER G. An offspring of multivariate extreme value theory: The max-characteristic function[J]. Journal of Multivariate Analysis, 2017, 154: 85–95. doi: 10.1016/j.jmva.2016.10.007. [18] 刘盛启. 基于高分辨距离像的特征提取与识别增强技术研究[D]. [博士论文], 国防科学技术大学, 2016.LIU Shengqi. Research on feature extraction and recognition performance enhancement algorithms based on high range resolution profile[D]. [Ph. D. dissertation], National University of Defense Technology, 2016. [19] AL-LABADI L and ZAREPOUR M. Two-sample Kolmogorov-Smirnov test using a Bayesian nonparametric approach[J]. Mathematical Methods of Statistics, 2017, 26(3): 212–225. doi: 10.3103/S1066530717030048. [20] 刘振. 基于稀疏表示的图像分类若干新方法研究[D]. [博士论文], 江南大学, 2021. doi: 10.27169/d.cnki.gwqgu.2021.001957.LIU Zhen. Research on new methods of image classification via sparse representation[D]. [Ph. D. dissertation], Jiangnan University, 2021. doi: 10.27169/d.cnki.gwqgu.2021.001957. [21] 缪吴霞. SAR图像回波反演及典型目标特征提取方法研究[D]. [硕士论文], 哈尔滨工业大学, 2019. doi: 10.27061/d.cnki.ghgdu.2019.001165.MIAO Wuxia. Research on SAR image echo inversion and typical target featuer extraction method[D]. [Master dissertation], Harbin Institute of Technology, 2019. doi: 10.27061/d.cnki.ghgdu.2019.001165. -





 下载:
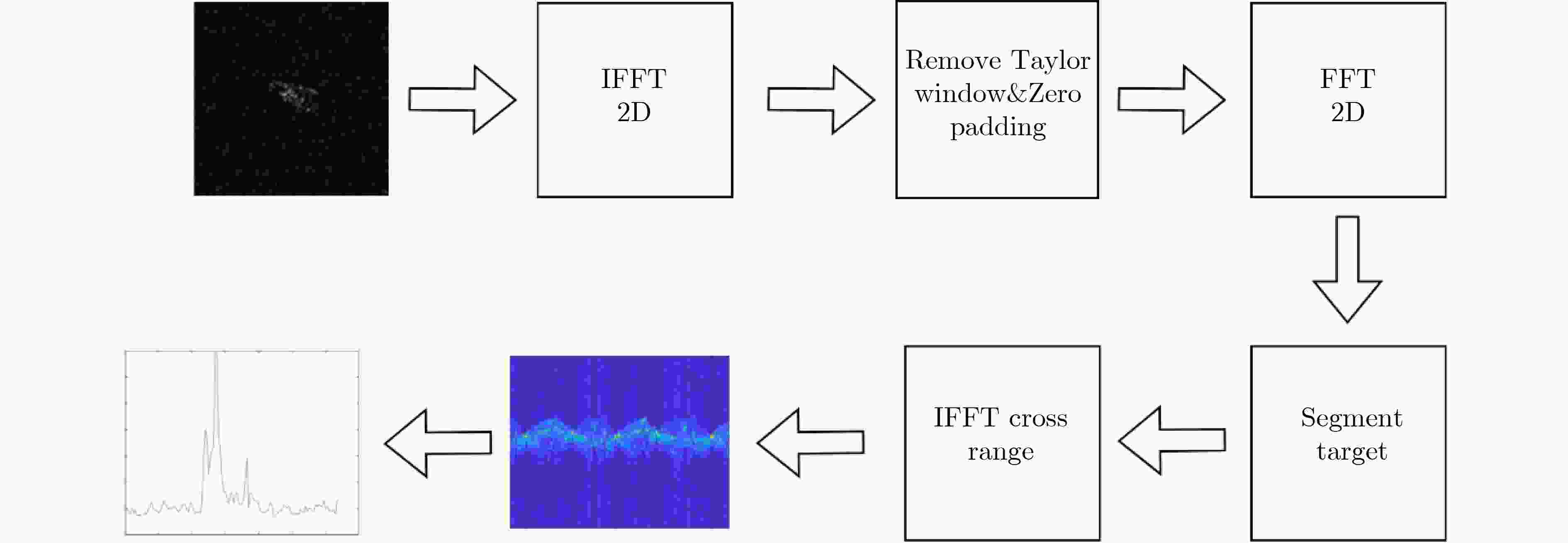
下载:


 下载:
下载:
