Max-min Rate Optimization Algorithm for Non-Orthogonal Multiple Access Backscatter Communication System Assisted by Unmanned Aerial Vehicles
-
摘要: 无人机(UAV)、非正交多址(NOMA)和反向散射通信(BC)相结合，可以满足热点地区高容量需求，提高通信质量。该文提出一种无人机辅助的NOMA反向散射通信系统最小速率最大化资源分配算法。考虑无人机发射功率、能量收集、反射系数、传输速率以及连续干扰消除(SIC)解码顺序约束，建立基于系统最小速率最大化的资源分配模型。首先利用块坐标下降将原问题分解为无人机发射功率优化、反射系数优化和无人机位置与SIC解码顺序联合优化3个子问题，然后使用反证法给出无人机最优发射功率，再用变量替换法和连续凸逼近将剩余子问题进一步转化为凸优化问题进行求解。仿真结果表明，所提算法在系统和速率与用户公平性之间具有较好折中。Abstract: The combination of Unmanned Aerial Vehicle (UAV), Non-Orthogonal Multiple Access (NOMA), and Backscatter Communication (BC) can meet the high capacity demand and improve the communication quality in hotspots. A max-min rate optimization algorithm is proposed for UAV-assisted NOMA-based backscatter communication systems. Specifically, a resource allocation model is developed to maximize systems’ minimum rate under the UAV transmit power, energy harvesting, reflection coefficient, transmission rate, and Successive Interference Cancellation (SIC) decoding order constraints. The original problem is divided into three subproblems: UAV transmit power optimization, reflection coefficient optimization, and joint optimization of UAV position and SIC decoding order optimization, which are handled by block coordinated decent method. Then, the UAV’s optimal transmit power optimization subproblem is solved by contradiction. Furthermore, the remaining subproblems are solved by convex optimization with variable substitution and successive convex approximation methods. Finally, the simulation results show that the proposed algorithm has obtained a good tradeoff between the systems’ sum rate and users’ fairness.
-
算法1 最小速率最大化资源分配算法 初始化：max-min速率$R_{\max - \min }^0$，内层迭代次数$ l = 0 $，外层迭
代次数$ t = 0 $，惩罚参数$\mu = {\mu _0}$，步长$\gamma = {\gamma _0}$；无人机最大发射
功率$ {P_{\max }} $，$ {{\mathbf{q}}^0},{{\mathbf{A}}^0},{{\mathbf{B}}^0},{{\mathbf{C}}^0},{{\mathbf{U}}^0},{{\mathbf{G}}^0} $；max-min速率收敛精度
$ {\varsigma _1} $，惩罚收敛精度$ {\varsigma _2} $，外层最大迭代次数为$ {T_{\max }} $；(1) repeat (2) repeat (3) 根据给定的$ {{\mathbf{q}}^l} $和$ {{\mathbf{A}}^l} $利用凸优化内点法求解问题式(9)得
到反射系数$ {{\mathbf{R}}^*} $；(4) 根据$ {{\mathbf{R}}^*},{{\mathbf{B}}^l},{{\mathbf{C}}^l},{{\mathbf{U}}^l},{{\mathbf{G}}^l} $利用凸优化内点法求解问题
式(22)得到无人机位置$ {{\mathbf{q}}^*} $和SIC解码顺序$ {{\mathbf{A}}^*} $；(5) 更新$ l = l + 1 $； (6) until $ \left| {R_{\max - \min }^{l + 1} - R_{\max - \min }^l} \right| < {\varsigma _1} $； (7) if $ \max \left\{ {{\varphi _{nm}}} \right\} \gt {\varsigma _2} $ (8) 更新$ \mu = \gamma \mu $； (9) else (10) 更新$ t = t + 1 $； (11) end if (12) until $t \ge {T_{\max } }$。 
下载: 导出CSV
-
[1] AL-FUQAHA A, GUIZANI M, MOHAMMADI M, et al. Internet of things: A survey on enabling technologies, protocols, and applications[J]. IEEE Communications Surveys & Tutorials, 2015, 17(4): 2347–2376. doi: 10.1109/COMST.2015.2444095 [2] VAN HUYNH N, HOANG D T, LU Xiao, et al. Ambient backscatter communications: A contemporary survey[J]. IEEE Communications Surveys & Tutorials, 2018, 20(4): 2889–2922. doi: 10.1109/COMST.2018.2841964 [3] BOYER C and ROY S. Backscatter communication and RFID: Coding, energy, and MIMO analysis[J]. IEEE Transactions on Communications, 2014, 62(3): 770–785. doi: 10.1109/TCOMM.2013.120713.130417 [4] WANG Zhe, DUAN Lingjie, and ZHANG Rui. Adaptive deployment for UAV-aided communication networks[J]. IEEE Transactions on Wireless Communications, 2019, 18(9): 4531–4543. doi: 10.1109/TWC.2019.2926279 [5] WANG Zhengqiang, CHENG Qu, FAN Zifu, et al. A review of resource allocation studies for non-orthogonal multiple access system[J]. Telecommunication Science, 2018, 34(8): 136–146. doi: 10.11959/j.issn.1000-0801.2018236 [6] XU Yongjun and GUI Guan. Optimal resource allocation for wireless powered multi-carrier backscatter communication networks[J]. IEEE Wireless Communications Letters, 2020, 9(8): 1191–1195. doi: 10.1109/LWC.2020.2985010 [7] KHAN W U, LI Xingwang, ZENG Ming, et al. Backscatter-enabled NOMA for future 6G systems: A new optimization framework under imperfect SIC[J]. IEEE Communications Letters, 2021, 25(5): 1669–1672. doi: 10.1109/LCOMM.2021.3052936 [8] XU Yongjun, QIN Zhijin, GUI Guan, et al. Energy efficiency maximization in NOMA enabled backscatter communications with QoS guarantee[J]. IEEE Wireless Communications Letters, 2021, 10(2): 353–357. doi: 10.1109/LWC.2020.3031042 [9] YANG Gang, DAI Rao, and LIANG Yingchang. Energy-efficient UAV backscatter communication with joint trajectory design and resource optimization[J]. IEEE Transactions on Wireless Communications, 2021, 20(2): 926–941. doi: 10.1109/TWC.2020.3029225 [10] FARAJZADEH A, ERCETIN O, and YANIKOMEROGLU H. UAV data collection over NOMA backscatter networks: UAV altitude and trajectory optimization[C]. 2019 IEEE International Conference on Communications, Shanghai, China, 2019: 1–7. [11] GRANT M and BOYD S. CVX: Matlab software for disciplined convex programming[EB/OL]. http://cvxr.com/cvx, 2020. [12] ZHANG Ningbo, WANG Jing, KANG Guixia, et al. Uplink nonorthogonal multiple access in 5G systems[J]. IEEE Communications Letters, 2016, 20(3): 458–461. doi: 10.1109/LCOMM.2016.2521374 [13] LU Jinhui, WANG Yuntian, LIU Tingting, et al. UAV-enabled uplink non-orthogonal multiple access system: Joint deployment and power control[J]. IEEE Transactions on Vehicular Technology, 2020, 69(9): 10090–10102. doi: 10.1109/TVT.2020.3005732 [14] VU Q D, NGUYEN K G, and JUNTTI M. Max-min fairness for multicast multigroup multicell transmission under backhaul constraints[C]. 2016 IEEE Global Communications Conference, Washington, USA, 2016: 1–6. [15] NGUYEN T M, AJIB W, and ASSI C. A novel cooperative NOMA for designing UAV-assisted wireless backhaul networks[J]. IEEE Journal on Selected Areas in Communications, 2018, 36(11): 2497–2507. doi: 10.1109/JSAC.2018.2874136 [16] WANG Zhengqiang, DU Jin, FAN Zifu, et al. Energy efficiency maximization for multi-carrier cooperative non-orthogonal multiple access systems[J]. Digital Signal Processing, 2022, 130: 103725. doi: 10.1016/j.dsp.2022.103725 [17] LI Dong. Two birds with one stone: Exploiting decode-and-forward relaying for opportunistic ambient backscattering[J]. IEEE Transactions on Communications, 2020, 68(3): 1405–1416. doi: 10.1109/TCOMM.2019.2957490 [18] CHEN Zhiyong, DING Zhiguo, DAI Xuchu, et al. An optimization perspective of the superiority of NOMA compared to conventional OMA[J]. IEEE Transactions on Signal Processing, 2017, 65(19): 5191–5202. doi: 10.1109/TSP.2017.2725223 [19] WANG Zhengqiang, WAN Xiaoyu, WEI Xiao, et al. A closed-form power control algorithm in cognitive radio networks based on Nash bargaining solution[C]. The 3rd IEEE International Conference on Computer and Communications, Chengdu, China, 2017: 681–685. [20] LI Xingwang, ZHENG Yike, KHAN W U, et al. Physical layer security of cognitive ambient backscatter communications for green Internet-of-Things[J]. IEEE Transactions on Green Communications and Networking, 2021, 5(3): 1066–1076. doi: 10.1109/TGCN.2021.3062060 [21] ZHANG Yanliang, HE Wenjing, LI Xingwang, et al. Covert communication in downlink NOMA systems with channel uncertainty[J]. IEEE Sensors Journal, 2022, 22(19): 19101–19112. doi: 10.1109/JSEN.2022.3201319 [22] LI Geng, LIU Huiling, HUANG Gaojian, et al. Effective capacity analysis of reconfigurable intelligent surfaces aided NOMA network[J]. EURASIP Journal on Wireless Communications and Networking, 2021, 2021(1): 198. doi: 10.1186/s13638-021-02070-7 [23] HUA Meng and WU Qingqing. Throughput maximization for IRS-aided MIMO FD-WPCN with non-linear EH model[J]. IEEE Journal of Selected Topics in Signal Processing, 2022, 16(5): 918–932. doi: 10.1109/JSTSP.2022.3179840 [24] LI Xingwang, ZHAO Mengle, ZENG Ming, et al. Hardware impaired ambient backscatter NOMA systems: Reliability and security[J]. IEEE Transactions on Communications, 2021, 69(4): 2723–2736. doi: 10.1109/TCOMM.2021.3050503 -
图(5) / 表(1)
计量
- 文章访问数: 754
- HTML全文浏览量: 237
- PDF下载量: 169
- 被引次数: 0
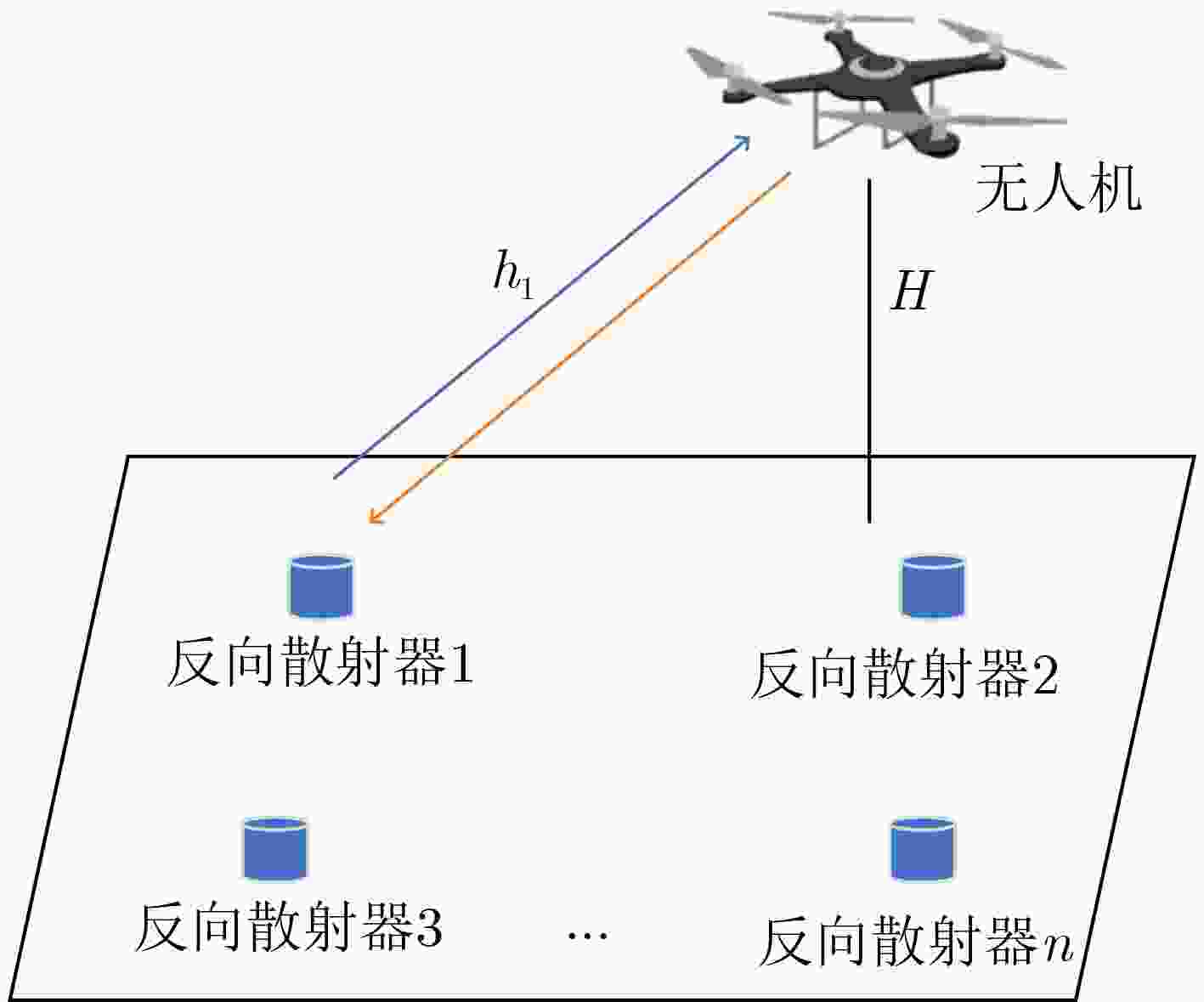
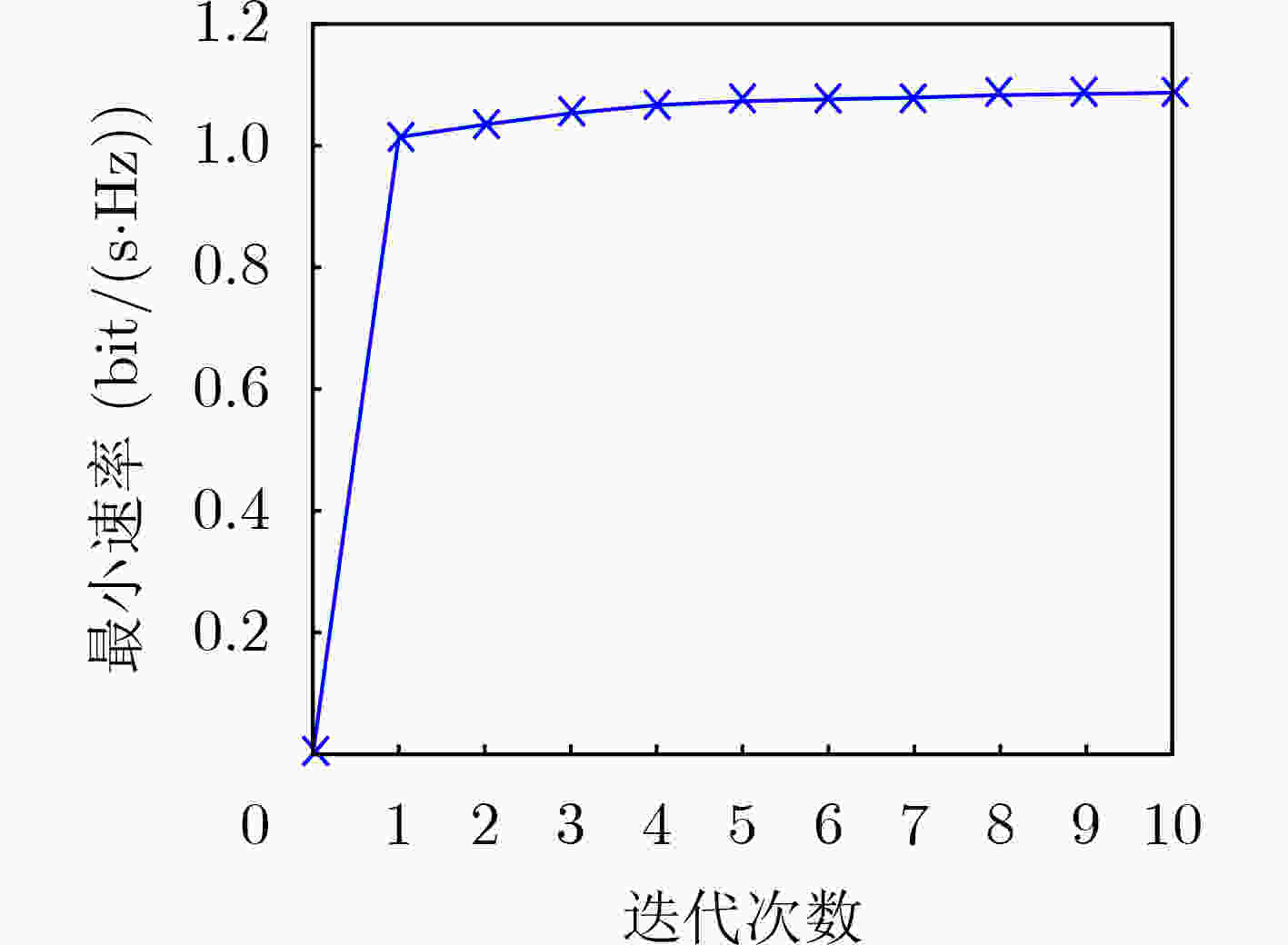
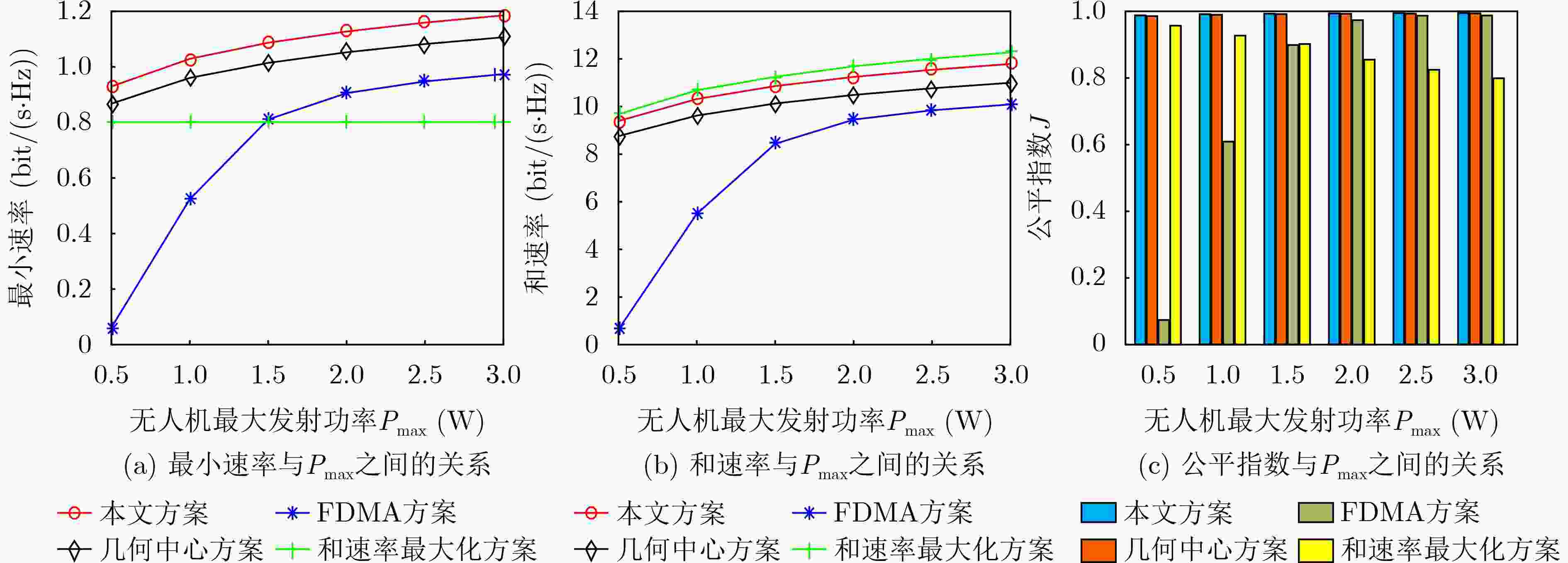
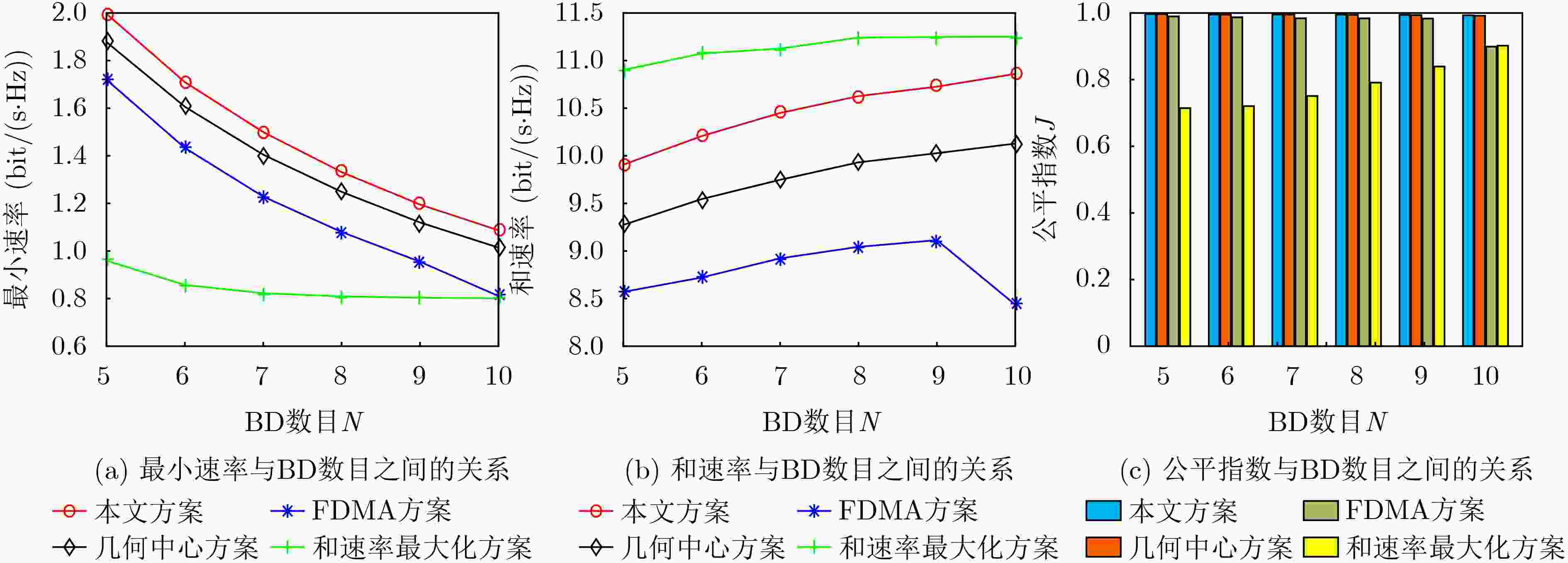
下载:
