Personalized Federated Learning Method Based on Collation Game and Knowledge Distillation
-
摘要: 为克服联邦学习(FL)客户端数据和模型均需同构的局限性并且提高训练精度,该文提出一种基于合作博弈和知识蒸馏的个性化联邦学习(pFedCK)算法。在该算法中,每个客户端将在公共数据集上训练得到的局部软预测上传到中心服务器并根据余弦相似度从服务器下载最相近的k个软预测形成一个联盟,然后利用合作博弈中的夏普利值来衡量客户端之间多重协作的影响,量化所下载软预测对本地个性化学习效果的累计贡献值,以此确定联盟中每个客户端的最佳聚合系数,从而得到更优的聚合模型。最后采用知识蒸馏将聚合模型的知识迁移到本地模型,并在隐私数据集上进行本地训练。仿真结果表明,与其他算法相比,pFedCK算法可以将个性化精度提升约10%。Abstract: To overcome the limitation of the Federated Learning (FL) when the data and model of each client are all heterogenous and improve the accuracy, a personalized Federated learning algorithm with Collation game and Knowledge distillation (pFedCK) is proposed. Firstly, each client uploads its soft-predict on public dataset and download the most correlative of the k soft-predict. Then, this method apply the shapley value from collation game to measure the multi-wise influences among clients and quantify their marginal contribution to others on personalized learning performance. Lastly, each client identify it’s optimal coalition and then distill the knowledge to local model and train on private dataset. The results show that compared with the state-of-the-art algorithm, this approach can achieve superior personalized accuracy and can improve by about 10%.
-
算法1 pFedCK算法 输入:初始化模型参数${{\boldsymbol{\omega}} ^0} = \left[ {{\boldsymbol{\omega}} _1^0,{\boldsymbol{\omega}} _{^2}^0, \cdots ,{\boldsymbol{\omega}} _n^0} \right]$ 输出: ${\boldsymbol{\omega}} = \left[ { {{\boldsymbol{\omega}} _{^1} },{{\boldsymbol{\omega}} _{^2} }, \cdots ,{{\boldsymbol{\omega}} _{^n} } } \right]$ Begin: (1)初始化客户端模型参数${{\boldsymbol{\omega}} ^0} = \left[ {{\boldsymbol{\omega}} _1^0,{\boldsymbol{\omega}} _{^2}^0, \cdots ,{\boldsymbol{\omega}} _n^0} \right]$ (2)迁移学习:客户端 i在${{\boldsymbol{D}}_{\rm{p}}}$和${{\boldsymbol{D}}_i}$上训练到收敛 (3) for t in 全局迭代次数: (4) for i in range(${\boldsymbol{N}}$): (5) 在${{\boldsymbol{D}}_{\rm{p}}}$上得到$ logi{t_i} $并上传到中心服务器形成$\left\{ {{\rm{logit}}_i^t} \right\}_{i = 1}^n$,根据余弦相似度 (6) 下载k个最相近的软预测并形成合作博弈$\left( { { {\left\{ {{\rm{logit}}_j^t} \right\} }_{j \in S_k^t} },v} \right)$ (7) for j in ${\boldsymbol{S}}_k^t$: (8) for ${\boldsymbol{X}} \subseteq {\boldsymbol{S}}_k^t$: (9) $\varphi _j^t\left( v \right) = \varphi _j^t\left( v \right) + \dfrac{ {\left( {\left| {\boldsymbol{X} } \right| - 1} \right)!\left( {\left| {\boldsymbol{S} } \right| - \left| {\boldsymbol{X} } \right|} \right)} }{ {\left| {\boldsymbol{S} } \right|!} } \cdot \left[ {v\left( {\boldsymbol{X}} \right) - v\left( {{\boldsymbol{X}}/\left\{ j \right\} } \right)} \right]$ (10) $\theta _j^t = \dfrac{ {\max\left( {\varphi _j^t,0} \right)} }{ {\left\| { {\rm{logit} }_i^t - {\rm{logit} }_j^t} \right\|} }$ (11) $\theta _j^{t*} = \dfrac{ {\theta _j^t} }{ {\displaystyle\sum\limits_j {\theta _j^t} } }$ (12) ${\rm{logit} }_i^{t*} = p \cdot { {\rm{logit} }_i} + q \cdot \displaystyle\sum\limits_j {\theta _j^{t*} \cdot { {\rm{logit} }_j} }$ (13) ${ {\boldsymbol{\omega} } _i} = { {\boldsymbol{\omega} } _i} - {\eta _1} \cdot \lambda \cdot { {\boldsymbol{\nabla} } _{ { {\boldsymbol{\omega} } _i} } }{L_{KL} }\left( { {\rm{logit} }_i^{t*},{ {\rm{logit} }_i};{{\boldsymbol{D}}_{\rm{p}}} } \right) - {\eta _2} \cdot {{\boldsymbol{\nabla}} _{ {{\boldsymbol{\omega}} _i} } }{L_i}\left( { {\omega _i};{{\boldsymbol{D}}_i} } \right)$ End 表 1 4种算法在不同数据集下的个性化精度
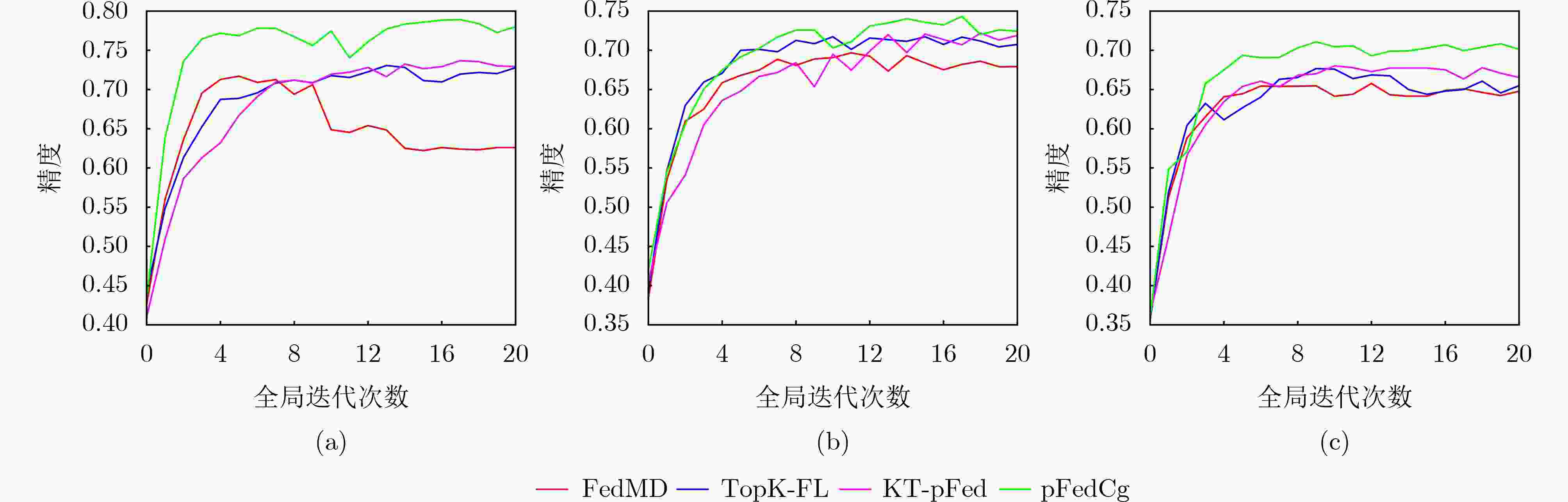
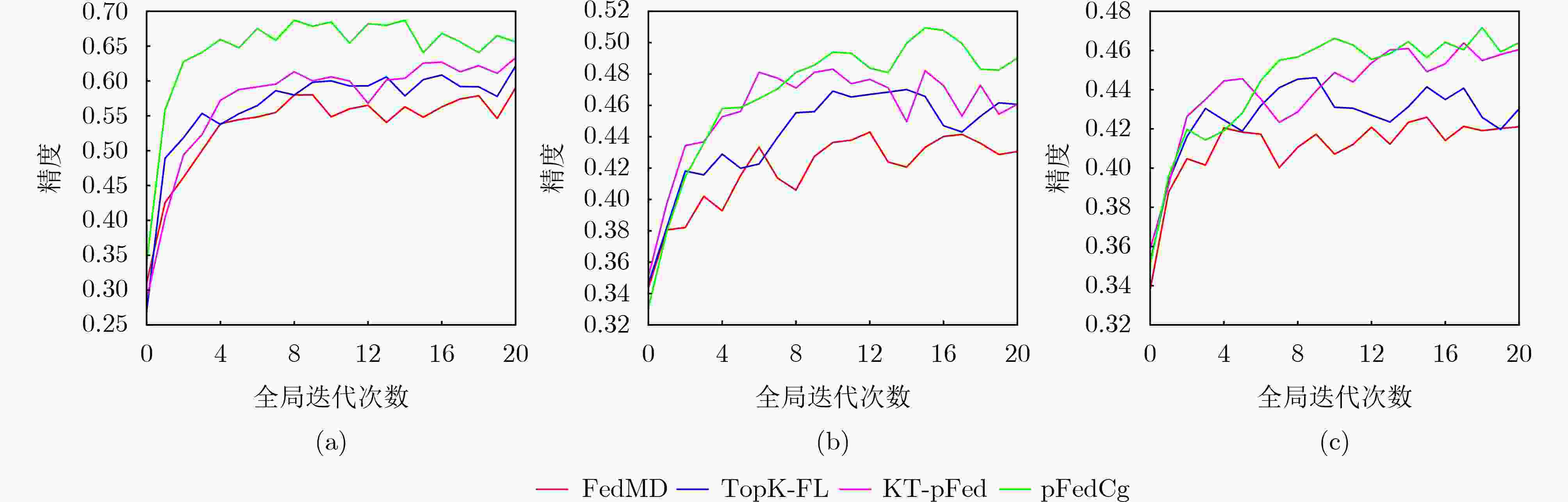
MNIST-EMNIST CIFAR10-CIFAR100 IID Non-IID1 Non-IID2 IID Non-IID1 Non-IID2 FedMD 0.7128 0.6967 0.6577 0.5902 0.4430 0.4206 TopK-FL 0.7307 0.7173 0.6767 0.6215 0.4701 0.4513 KT-pFed 0.7368 0.7218 0.6802 0.6333 0.4831 0.4639 pFedCK 0.7819 0.7422 0.7156 0.6869 0.5064 0.4717 表 2 不同本地迭代次数下pFedCK算法的个性化精度
数据集 本地迭代次数 5 10 15 20 MNIST-EMNIST IID 0.7503 0.7833 0.7638 0.7753 Non-IID1 0.7379 0.7310 0.7216 0.7422 Non-IID2 0.7069 0.7013 0.7140 0.7156 CIFAR10-CIFAR100 IID 0.6559 0.6555 0.6872 0.6365 Non-IID 0.4604 0.4817 0.4697 0.5064 Non-IID2 0.4558 0.4687 0.4513 0.4717 表 3 不同本地蒸馏次数下pFedCK算法的个性化精度
数据集 本地蒸馏次数 1 2 3 5 MNIST-EMNIST IID 0.7595 0.7679 0.7772 0.7861 Non-IID1 0.7174 0.7116 0.7422 0.7248 Non-IID2 0.7025 0.7083 0.7156 0.7133 CIFAR10-CIFAR100 IID 0.6530 0.6458 0.6869 0.6836 Non-IID1 0.4942 0.5078 0.4837 0.5024 Non-IID2 0.4620 0.4732 0.4717 0.4597 表 4 不同
$ p - q $ 下pFedCK算法的个性化精度数据集 $ p,q $ 0.1,0.9 0.2,0.8 0.3,0.7 0.4,0.6 MNIST-EMNIST IID 0.7885 0.7842 0.7770 0.7631 Non-IID1 0.7214 0.7407 0.7378 0.7435 Non-IID2 0.7038 0.6997 0.7156 0.7104 CIFAR10-CIFAR100 IID 0.6737 0.6450 0.6869 0.6610 Non-IID1 0.4915 0.4720 0.5064 0.4749 Non-IID2 0.4663 0.4532 0.4717 0.4750 表 5 不同λ下pFedCK算法的个性化精度
数据集 λ 0.1 0.3 0.5 0.8 MNIST-EMNIST IID 0.7843 0.7732 0.7819 0.7791 Non-IID1 0.7404 0.7457 0.7422 0.7387 Non-IID2 0.7167 0.7203 0.7156 0.7052 CIFAR10-CIFAR100 IID 0.6106 0.6263 0.6869 0.6843 Non-IID1 0.4861 0.4982 0.5064 0.5105 Non-IID2 0.4676 0.4532 0.4717 0.4747 -
[1] MCMAHAN B, MOORE E, RAMAGE D, et al. Communication-efficient learning of deep networks from decentralized data[C]. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, USA, 2017: 1273–1282. [2] LI Tian, SAHU A K, TALWALKAR A, et al. Federated learning: Challenges, methods, and future directions[J]. IEEE Signal Processing Magazine, 2020, 37(3): 50–60. doi: 10.1109/MSP.2020.2975749 [3] ARIVAZHAGAN M G, AGGARWAL V, SINGH A K, et al. Federated learning with personalization layers[EB/OL]. https://doi.org/10.48550/arXiv.1912.00818, 2019. [4] HANZELY F and RICHTÁRIK P. Federated learning of a mixture of global and local models[EB/OL]. https://doi.org/10.48550/arXiv.2002.05516, 2020. [5] FALLAH A, MOKHTARI A, and OZDAGLAR A E. Personalized federated learning with theoretical guarantees: A model-agnostic meta-learning approach[C]. Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2020: 3557–3568. [6] GHOSH A, CHUNG J, YIN D, et al. An efficient framework for clustered federated learning[C]. Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2020: 19586–19597. [7] WU Leijie, GUO Song, DING Yaohong, et al. A coalition formation game approach for personalized federated learning[EB/OL]. https://doi.org/10.48550/arXiv.2202.02502, 2022. [8] HINTON G, VINYALS O, and DEAN J. Distilling the knowledge in a neural network[J]. Computer Science, 2015, 14(7): 38–39. [9] LI Daliang and WANG Junpu. FedMD: Heterogenous federated learning via model distillation[EB/OL]. https://doi.org/10.48550/arXiv.1910.03581, 2019. [10] LIN Tao, KONG Lingjing, STICH S U, et al. Ensemble distillation for robust model fusion in federated learning[C]. Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2020: 2351–2363. [11] ZHANG Jie, GUO Song, MA Xiaosong, et al. Parameterized knowledge transfer for personalized federated learning[C]. Proceedings of the 35th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2021: 10092–10104. [12] CHO Y J, WANG Jianyu, CHIRUVOLU T, et al. Personalized federated learning for heterogeneous clients with clustered knowledge transfer[EB/OL]. https://doi.org/10.48550/arXiv.2109.08119, 2021. [13] DONAHUE K and KLEINBERG J. Model-sharing games: Analyzing federated learning under voluntary participation[C]. Proceedings of the 35th AAAI Conference on Artificial Intelligence, Vancouver, Canada, 2021: 5303–5311. [14] LUNDBERG S M and LEE S I. A unified approach to interpreting model predictions[C]. Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 4768–4777. [15] SAAD W, HAN Zhu, DEBBAH M, et al. Coalitional game theory for communication networks[J]. IEEE Signal Processing Magazine, 2009, 26(5): 77–97. doi: 10.1109/MSP.2009.000000 -





 下载:
下载:



 下载:
下载:
