A Low Complexity Millimeter Wave Channel Tracking Algorithm in Reconfigurable Intelligent Surface
-
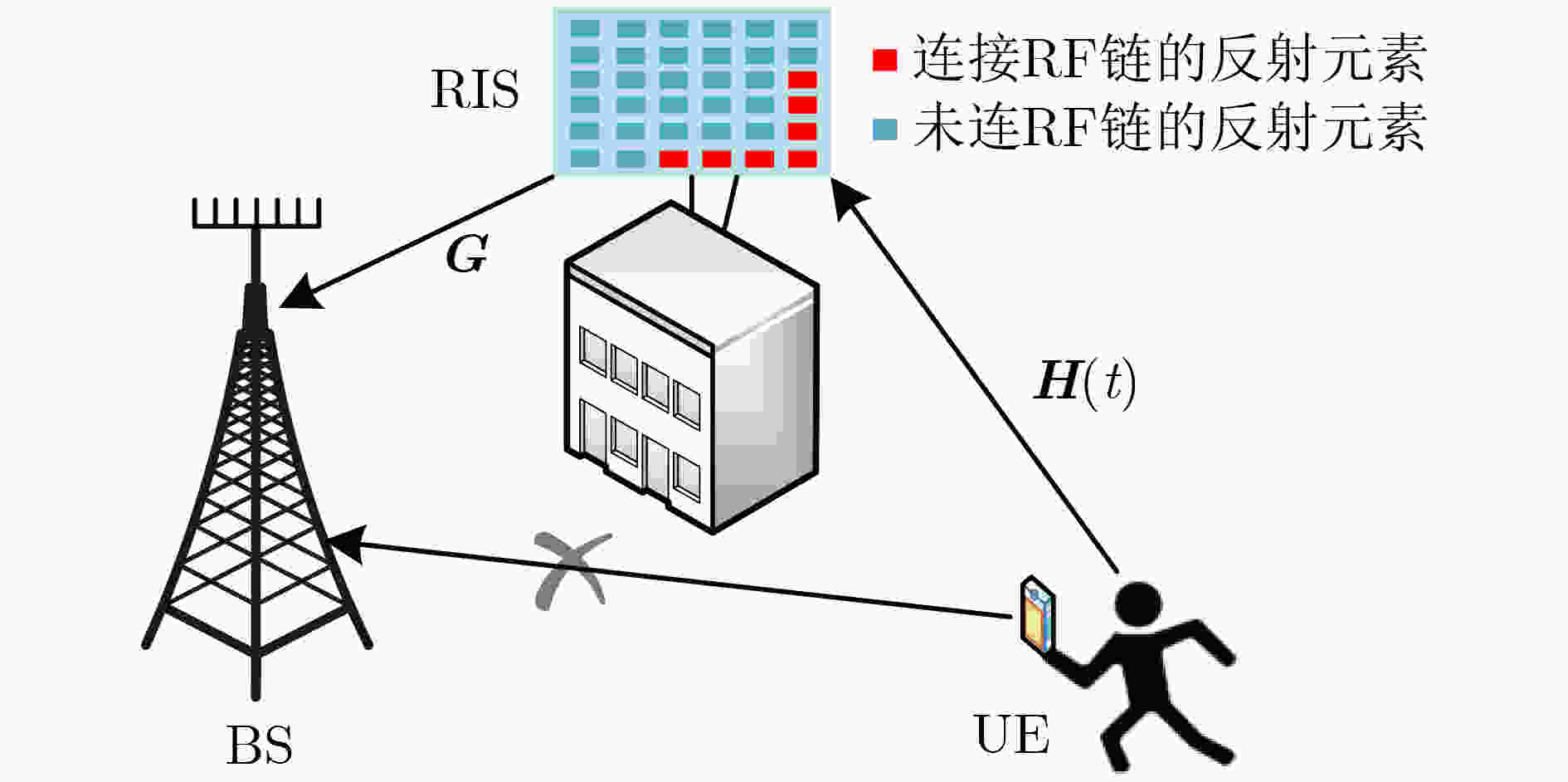
摘要: 针对可重构智能表面(RIS)中的毫米波通信系统,用户至RIS端信道角度参数的缓慢变化,该文提出一种基于牛顿算法的低复杂度信道追踪方案。该方案将RIS部分元件连接射频(RF)链,首先使用2维快速傅里叶变换 (2D-FFT)算法初始化估计角度,并且使用最大似然算法估计路径增益。在后续时隙中,使用牛顿算法追踪每个时隙的角度参数。由于环境突然变化和终端缓慢变化会导致信道矩阵发生突变,若检测到信道突变,则再次初始化参数,否则使用牛顿算法继续追踪角度参数。仿真结果表明,该方案在具有优良性能的前提下复杂度可以达到最低,极大节约算力资源,在计算复杂度和性能之间可以取得很好的平衡。Abstract: In this paper, a low complexity channel tracking scheme based on Newton algorithm is proposed for the millimeter wave communication system assisted by Reconfigurable Intelligent Surfaces (RIS). The proposed tracking algorithm is used to track the slow variation of the angle between the user and the RIS. In the proposed scheme, some elements of RIS are connected to the Radio Frequency (RF) chains. The two-Dimensional Fast Fourier Transform (2D-FFT) algorithm is used to initialize the angle estimation, and then the Newton algorithm is used to track the angle parameters in each time slot. The channel gain of each slot is estimated by maximum likelihood algorithm. The channel abrupt changes is caused by sudden environmental change and slow change of user terminal. If the abrupt change is detected, the angle parameters are initialized again, otherwise the Newton algorithm is still used to track the angle parameters. Simulation results show that the proposed channel tracking scheme not only achieves the lowest complexity but also ensures excellent performance, which achieves a great tradeoff between computational complexity and channel estimation performance.
-
算法1 基于牛顿算法的信道追踪方案 输入:时隙数:$ t = 1,2,\cdots,I $;导频信号:${\boldsymbol{\varGamma}} (t)$;RIS接收信号:${\boldsymbol{Y}}_{\text{R} }^{\text{h} }(t)$,${\boldsymbol{Y}}_{\text{R} }^{\text{v} }(t)$;BS接收信号:$ {\boldsymbol{Y}}(t) $;循环次数:$ {R_{\text{c}}} $ 输出:UE-RIS信道估计值$ {{\hat {\boldsymbol H}}}(t) $;RIS-BS信道估计值$ {{\hat {\boldsymbol G}}} $ for $ {l_a} = 1,2,\cdots,{L_a} $ (1)$ {\text{when }}t = 1 $,2D-FFT求解角度:根据式(15)、式(16)、式(17)分别计算$ \hat \varphi _{\boldsymbol{H}}^{{l_a}}(1),\hat \phi _{\boldsymbol{H}}^{{l_a}}(1),\hat \theta _{\boldsymbol{H}}^{{l_a}}(1) $,同理求解$ {\psi _{{l_b}}},{\gamma _{{l_b}}},{\varphi _{{l_b}}} $
ML求解路径增益:根据式(22)计算$ {a_{{l_a}}}(1) $,同理求解$ {b_{{l_b}}} $(2)for $ t = 2,3,\cdots,I $ for $ k = 1,2,\cdots,{R_{\text{c}}} $ $ \left[ \begin{gathered} {{\hat u}_{{l_a}}}{(t)^{(k)}} \\ {{\hat v}_{{l_a}}}{(t)^{(k)}} \\ \end{gathered} \right] = \left[ \begin{gathered} {{\hat u}_{{l_a}}}{(t)^{(k - 1)}} \\ {{\hat v}_{{l_a}}}{(t)^{(k - 1)}} \\ \end{gathered} \right] - {{\ddot {\boldsymbol E}}}({\hat u_{{l_a}}}(t - 1),{\hat v_{{l_a}}}(t - 1)) \cdot {{\dot {\boldsymbol E}}}({\hat u_{{l_a}}}(t - 1),{\hat v_{{l_a}}}(t - 1)) $ end for $ {\hat u_{{l_a}}}(t) = {\hat u_{{l_a}}}{(t)^{({R_{\text{c}}})}},{\hat v_{{l_a}}}(t) = {\hat v_{{l_a}}}{(t)^{({R_{\text{c}}})}} $ 求解角度:根据式(15)、式(16)分别计算$ \hat \varphi _{\boldsymbol{H}}^{{l_a}}(t),\hat \phi _{\boldsymbol{H}}^{{l_a}}(t) $,同理求解$ \hat \theta _{\boldsymbol{H}}^{{l_a}}(t) $ 估计增益:根据式(22)计算$ {a_{{l_a}}}(t) $ 信道突变检测:若$\ln (L({\boldsymbol{Y}}_{\text{R} }^{ {\text{h} }' }(t))) > \gamma$;返回步骤1 end for end for
(3)输出信道估计值$\hat {\boldsymbol{H} }(t) = \displaystyle\sum\nolimits_{ {l_a} = 1}^{ {L_a} } { { {\hat a}_{ {l_a} } }(t){\boldsymbol{a} }_{ {\text{UR} } }^{}(\hat \theta _{\boldsymbol{H} }^{ {l_a} }(t),\hat \phi _{\boldsymbol{H} }^{ {l_a} }(t)){ {{\boldsymbol{a} }_{\text{U} }^{\text{H} }(\hat \varphi _{\boldsymbol{H} }^{ {l_a} }(t))} } } {\text{, } }\hat {\boldsymbol{G} }{\text{ = } }\displaystyle\sum\nolimits_{ {l_b} = 1}^{ {L_b} } { { {\hat b}_{ {l_b} } }{ {\boldsymbol{a} }_{\text{B} } }({ {\hat \psi }_{ {l_b} } }){ {{\boldsymbol{a} }_{ {\text{RB} } }^{\text{H} }({ {\hat \gamma }_{ {l_b} } },{ {\hat \varphi }_{ {l_b} } })} } }$表 1 不同算法计算复杂度对比
所用算法 计算复杂度 LS算法 $ O({N_{\text{T}}}^3 + N_{\text{T}}^2(2(T - 1) + 1 + 2N_{\text{I}}^{}) + 2N_{\text{I}}^{}N_{\text{T}}^{}(T - 1) + {N_{\text{T}}}) $ LMMSE算法 $ O(2N_{\text{T}}^3 + N_{\text{T}}^2(2(T - 1) + 1 + 8N_{\text{I}}^{}) + 2N_{\text{I}}^{}N_{\text{T}}^{}(T - 2) + 4N_{\text{T}}^{}) $ KF算法 $O(16L_a^3 + {(L{N_{\text{T} } })^3} + {(L{N_{\text{T} } })^2}(4{L_a} + 1) + 2{L_a}^2(4L{N_{\text{T} } } + 3{N_{\text{T} } } + 2L + 1) + 2L{N_{\text{T} } }({L_a} + 1) - {L_a}L)$ 本文算法 $O(8{L_a}^3 + 2{L_a}^2(3{N_{\text{T} } } + 2L - 1) + ({L_a} - 1)(2L{N_{\text{T} } } + {N_{\text{T} } }(4L - 2) + 22{R_{\text{c} } }) + L{N_{\text{T} } }(2T - 1) - {L_a}L) \\$ 表 2 主要仿真参数设置
参数 数值 UE端天线数$ {N_{\text{T}}} $ $ 5 $ RIS端反射单元数$ {N_{\text{I}}} $ $ 40 $ BS端天线数$ {N_{\text{R}}} $ $ 64 $ RIS连接水平/竖直RF链数$ L $ $ 5 $ UE-RIS路径数$ {L_a} $ $ 1 $ 载波频率$ {f_{\text{c}}} $ $ 30{\text{ GHz}} $ UE端离开角$ \hat \varphi _{\mathbf{H}}^{{l_a}} $ $ {50^ \circ } $ RIS端仰角$ \theta _{\mathbf{H}}^{{l_a}} $和水平角$ \phi _{\mathbf{H}}^{{l_a}} $ $ {30}^{\circ }和{20}^{\circ } $ -
[1] HAN Huimei, ZHAO Jun, ZHAI Wenchao, et al. Reconfigurable intelligent surface aided power control for physical-layer broadcasting[J]. IEEE Transactions on Communications, 2021, 69(11): 7821–7836. doi: 10.1109/TCOMM.2021.3104871 [2] WU Qingqing and ZHANG Rui. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network[J]. IEEE Communications Magazine, 2020, 58(1): 106–112. doi: 10.1109/MCOM.001.1900107 [3] ZHENG Beixiong and ZHANG Rui. Intelligent reflecting surface-enhanced OFDM: Channel estimation and reflection optimization[J]. IEEE Wireless Communications Letters, 2020, 9(4): 518–522. doi: 10.1109/LWC.2019.2961357 [4] PANG Xiaowei, SHENG Min, ZHAO Nan, et al. When UAV meets IRS: Expanding air-ground networks via passive reflection[J]. IEEE Wireless Communications, 2021, 28(5): 164–170. doi: 10.1109/MWC.010.2000528 [5] YANG Liang, YANG Jinxia, XIE Wenwu, et al. Secrecy performance analysis of RIS-aided wireless communication systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 12296–12300. doi: 10.1109/TVT.2020.3007521 [6] HUR S, KIM T, LOVE D J, et al. Millimeter wave beamforming for wireless backhaul and access in small cell networks[J]. IEEE Transactions on Communications, 2013, 61(10): 4391–4403. doi: 10.1109/TCOMM.2013.090513.120848 [7] JENSEN T L and DE CARVALHO E. An optimal channel estimation scheme for intelligent reflecting surfaces based on a minimum variance unbiased estimator[C]. 2020 IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 2020: 5000–5004. [8] 李素月, 郝红婷, 王安红. IRS辅助的多天线系统下行链路低复杂度信道估计[J]. 电讯技术, 2022, 62(4): 466–472. doi: 10.3969/j.issn.1001-893x.2022.04.009LI Suyue, HAO Hongting, and WANG Anhong. Low-complexity channel estimation for IRS-aided multi-antenna downlink systems[J]. Telecommunication Engineering, 2022, 62(4): 466–472. doi: 10.3969/j.issn.1001-893x.2022.04.009 [9] HE Zhenqing and YUAN Xiaojun. Cascaded channel estimation for large intelligent metasurface assisted massive MIMO[J]. IEEE Wireless Communications Letters, 2020, 9(2): 210–214. doi: 10.1109/LWC.2019.2948632 [10] MAO Zhendong, PENG Mugen, and LIU Xiqing. Channel estimation for reconfigurable intelligent surface assisted wireless communication systems in mobility scenarios[J]. China Communications, 2021, 18(3): 29–38. doi: 10.23919/JCC.2021.03.003 [11] CAI Penghao, ZONG Jun, LUO Xiliang, et al. Downlink channel tracking for intelligent reflecting surface-aided FDD MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2021, 70(4): 3341–3353. doi: 10.1109/TVT.2021.3063138 [12] HE Jiguang, NGUYEN N T, SCHROEDER R, et al. Channel estimation and hybrid architectures for RIS-assisted communications[C]. 2021 Joint European Conference on Networks and Communications & 6G Summit, Porto, Portugal, 2021: 60–65. [13] HE Jiguang, WYMEERSCH H, and JUNTTI M. Channel estimation for RIS-aided mmWave MIMO systems via atomic norm minimization[J]. IEEE Transactions on Wireless Communications, 2021, 20(9): 5786–5797. doi: 10.1109/TWC.2021.3070064 [14] ALEXANDROPOULOS G C and VLACHOS E. A hardware architecture for reconfigurable intelligent surfaces with minimal active elements for explicit channel estimation[C]. 2020 IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 2020: 9175–9179. [15] TAHA A, ALRABEIAH M, and ALKHATEEB A. Enabling large intelligent surfaces with compressive sensing and deep learning[J]. IEEE Access, 2021, 9(1): 44304–44321. doi: 10.1109/ACCESS.2021.3064073 [16] CHEN Xiao, SHI Jianfeng, YANG Zhaohui, et al. Low-complexity channel estimation for intelligent reflecting surface-enhanced massive MIMO[J]. IEEE Wireless Communications Letters, 2021, 10(5): 996–1000. doi: 10.1109/LWC.2021.3054004 [17] FAN Dian, GAO Feifei, WANG Gongpu, et al. Angle domain signal processing-aided channel estimation for indoor 60-GHz TDD/FDD massive MIMO systems[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(9): 1948–1961. doi: 10.1109/JSAC.2017.2720938 [18] ZHANG Chuang, GUO Dongning, and FAN Pingyi. Tracking angles of departure and arrival in a mobile millimeter wave channel[C]. 2016 IEEE International Conference on Communications, Kuala Lumpur, Malaysia, 2016: 1–6. [19] ABATZOGLOU T J. A fast maximum likelihood algorithm for frequency estimation of a sinusoid based on newton's method[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(1): 77–89. doi: 10.1109/TASSP.1985.1164541 [20] MAMANDIPOOR B, RAMASAMY D, and MADHOW U. Newtonized orthogonal matching pursuit: Frequency estimation over the continuum[J]. IEEE Transactions on Signal Processing, 2016, 64(19): 5066–5081. doi: 10.1109/TSP.2016.2580523 [21] KAY S M. Fundamentals of Statistical Signal Processing[M]. Englewood Cliffs: Prentice Hall Press, 1993: 425–506. -





 下载:
下载:


 下载:
下载:
