Low-orbit Bistatic Frequency Modulated Continuous Wave SAR Imaging Method Based on Singular Value Decomposition
-
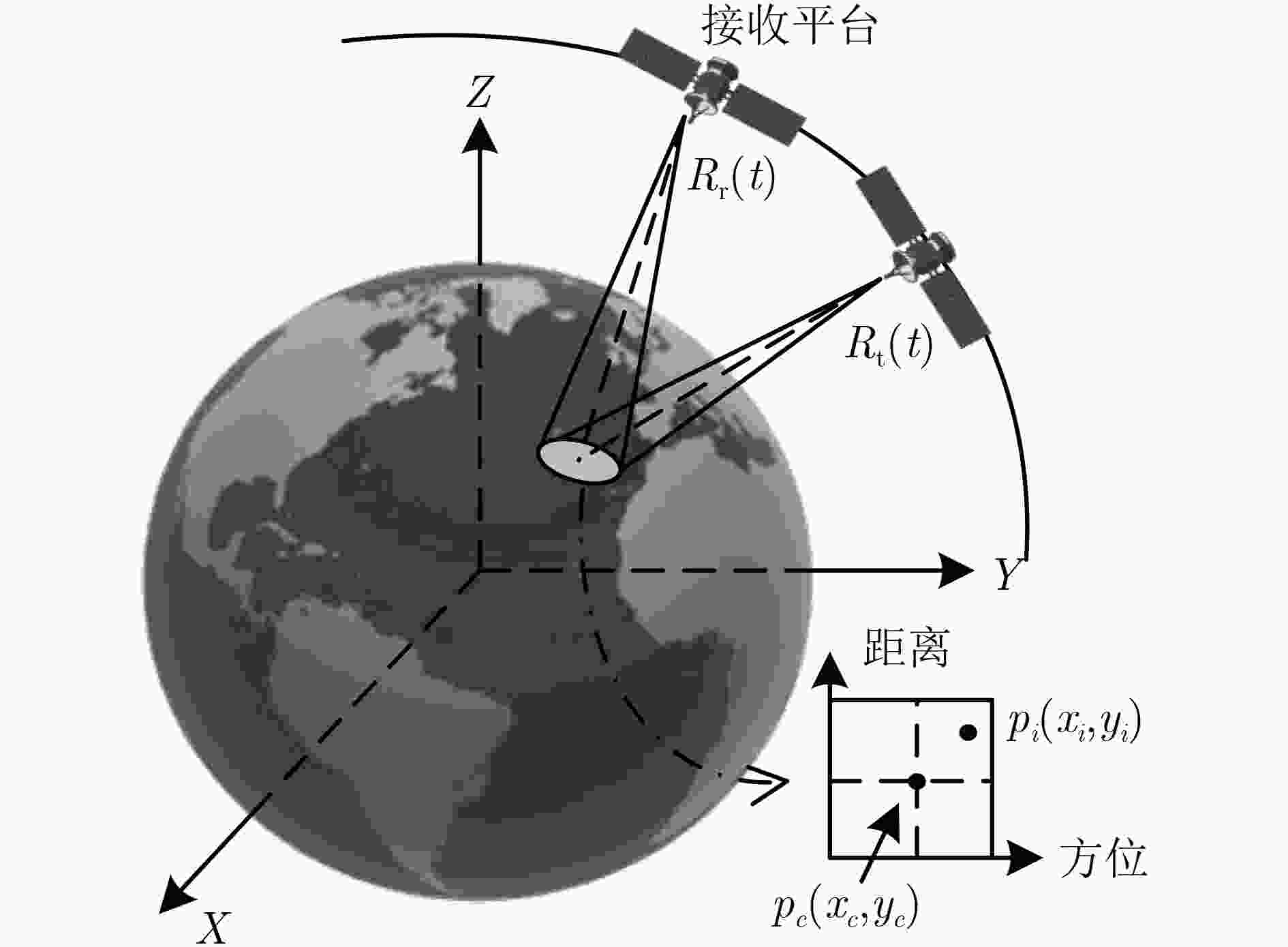
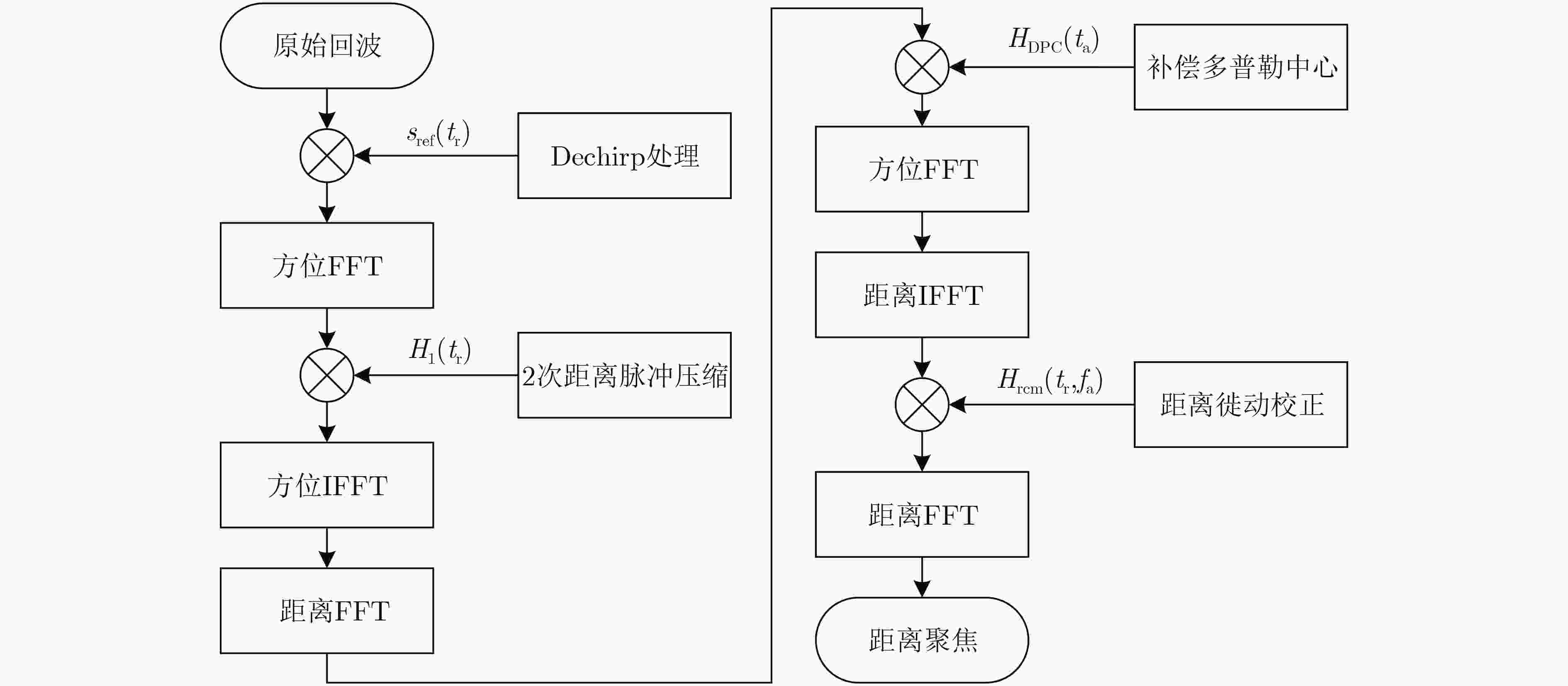
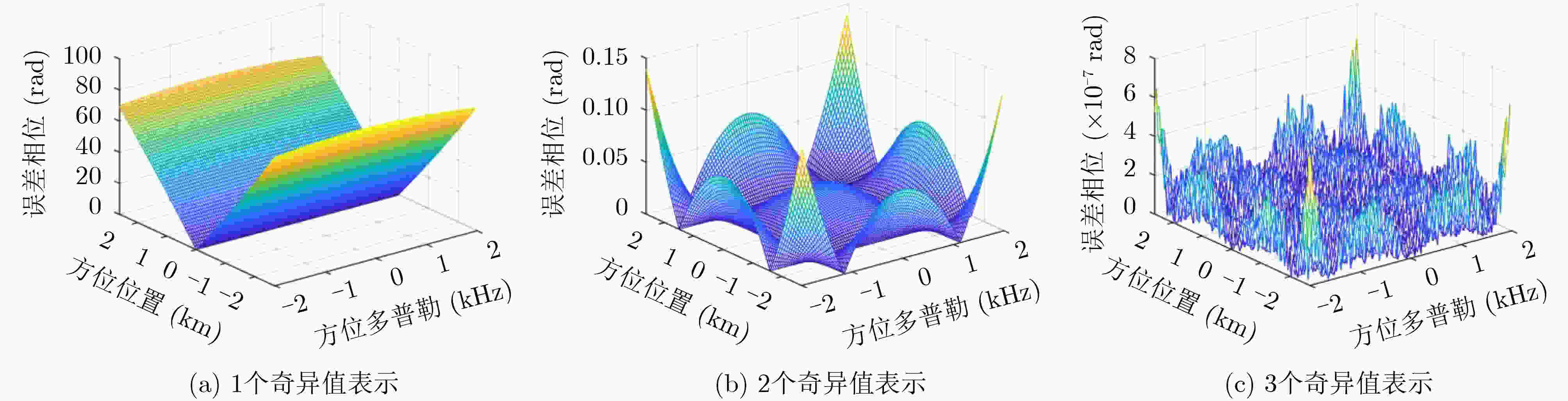
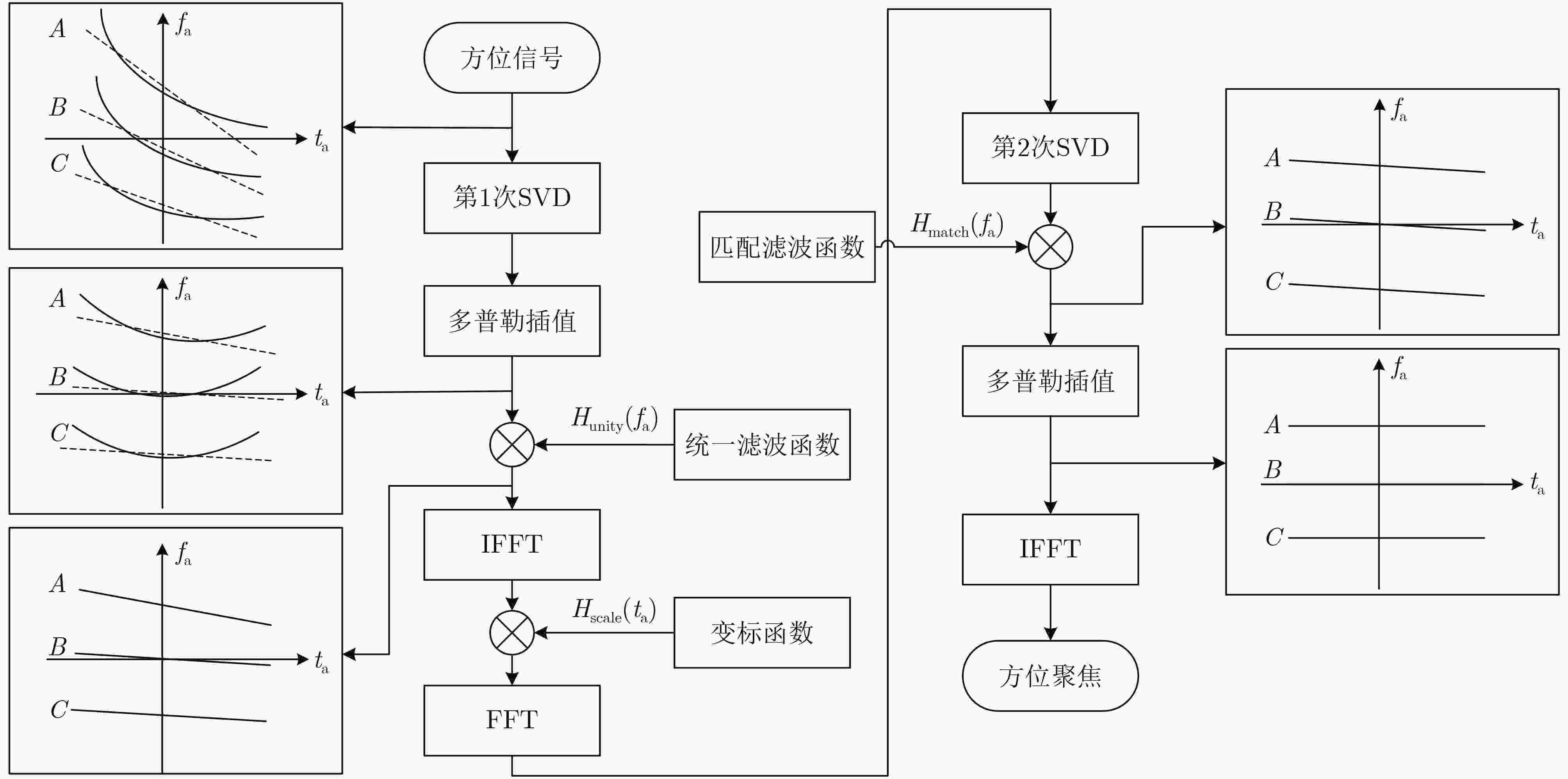
摘要: 该文基于调频连续波(FMCW)信号对低轨星载双基合成孔径雷达(SAR)的成像方法进行研究。星载双基模型具有收发异置、结构灵活的特点，其非线性运动轨迹和双斜距不利于信号频谱的推导和分析。通过引入一个4阶多项式斜距模型对回波信号进行建模，接着用级数反演法得到信号两维频谱的表达式。详细分析高阶多项式系数的空变影响。对距离徙动项进行频域处理，对方位相位采用奇异值分解(SVD)的方法，将方位空变项与多普勒分离开，并引入非线性方位变标函数，通过两次连续的插值和重采样完成方位聚焦。仿真结果证明了该算法的有效性。Abstract: The imaging method of low-orbit bistatic SAR based on Frequency Modulated Continuous Wave (FMCW) signal is studied in this paper. The spaceborne bistatic model has the feature of transceiver separation and flexible structure. The nonlinear motion trajectory and bistatic slant range history are not conducive to the derivation and analysis of signal spectrum. The signal is constructed by a fourth-order polynomial slant range model. The expression of the two-dimensional spectrum of the signal is obtained by the method of series reversion. The spatial variation effect of the high-order polynomial coefficients is analyzed in detail. The range migration term is compensated in frequency domain. The azimuth phase is processed by the Singular Value Decomposition (SVD) method. Then the azimuth spectrum is divided into Doppler focusing terms and azimuth variation terms. A nonlinear azimuth scaling function is introduced. The azimuth variation can be completely corrected by two consecutive interpolations and resampling. The validity of the proposed method is verified by the simulation experiments.
-
1. 引言
经过多年的发展，星载合成孔径雷达(Synthetic Aperture Radar, SAR)的理论研究已经十分成熟[1]。近年来，双基SAR (bistatic SAR)和多基SAR (multi-static SAR)逐渐成为SAR领域的热点研究内容之一。双基SAR相较于单基SAR具有隐蔽性好、能够多角度探测目标和系统灵活等优势受到研究人员的关注[2,3]。然而，由于星载双基SAR系统收发平台异构性较强，2维频谱与多普勒特性较难求取，2维分辨率在异构情况下可能带来成像畸变等问题，导致双基SAR系统的参数设计出现困难，随之也给成像算法的设计带来了挑战[4,5]。调频连续波雷达与传统脉冲雷达相比具有发射功率低，重量轻和成本低等优势，将其与星载双基构型相结合可以有效解决收发之间的耦合问题，同时由于其采用解线频调(dechirp)的处理方式，在对作用距离远、成像场景广等情况下可以明显降低采样率，提高处理效率。
双基调频连续波(Frequency Modulated Continuous Wave, FMCW) SAR成像具有3个主要特点：斜距模型更加复杂，传统SAR算法不再适用；方位空变同时存在于收发斜距历程中，方位平移不变性不再满足；成像处理流程复杂，两维频谱耦合严重。文献[6]提出了适用于线性轨迹的等效双斜距模型，将其等效为单基处理，并采用改进的距离多普勒(Range Doppler, RD)算法对目标进行成像，但忽略了星载轨道弯曲的影响；文献[7]对机动目标采用高阶多项式斜距代替非线性轨迹，处理过程中只考虑参考点的空变性，仅适用于小场景两维空变不严重的情况下，不适用于较大场景的处理。针对方位空变处理，文献[8]提出了基于Keystone和方位重采样的方法解决机载大斜视两维空变，其处理流程具有一定借鉴意义；文献[9]针对曲线轨迹提出一种级联的奇异值非线性变标方法校正高轨目标方位空变，采用奇异值分解的方法来分离多普勒项与方位位置的耦合，但其通过引入方位变标函数来去除奇异值分解残余项的方法不能完全收敛，存在高阶项相位未能完全补偿；文献[10]采用双基收发频谱分离的方法有效降低了谱计算的复杂度，但其也仍未考虑两维弯曲的空变影响。
针对双基FMCW SAR成像存在的问题，本文采用高阶多项式斜距模型，充分考虑脉内频移的影响，对距离维进行2次距离脉冲压缩、多普勒补偿和距离徙动矫正。方位维采用奇异值分解和引入改进的方位变标函数将影响方位空变的多普勒项和方位位置项分离开，并通过插值和重采样的方位校正方位空变项，经过频域滤波统一处理，最终在距离频域方位时域实现聚焦。本方法在保证成像效果的前提下，简化了信号处理的复杂性，点目标与面目标的仿真验证了算法的有效性。
2. 星载双基FMCW SAR信号模型
星载双基FMCW SAR成像几何模型如图1所示，卫星收发平台处于低轨同航线(发射在前，接收在后)，考虑到发射和接收平台的非线性轨迹，故收发平台的瞬时斜距可以表示为
Rr(t)=√(x0,r+vx,rt+12ax,rt2−xi)2+(y0,r+vy,rt+12ay,rt2−yi)2+(z0,r+vz,rt+12az,rt2−zi)2 (1) Rt(t)=√(x0,t+vx,tt+12ax,tt2−xi)2+(y0,t+vy,tt+12ay,tt2−yi)2+(z0,t+vz,tt+12az,tt2−zi)2 (2) 其中，t为全时间，可以表示为方位慢时间ta和距离快时间tr的和，即t=ta+tr。Rr(t)和Rt(t)分别表示收、发平台到目标点的瞬时斜距，pi=(xi,yi,zi)为目标点的坐标，(x0,t,vx,t,ax,t), (y0,t,vy,t,ay,t), (z0,t,vz,t,az,t)分别为发射卫星轨迹的3维运动参数，(x0,r,vx,r,ax,r), (y0,r,vy,r,ay,r), (z0,r,vz,r,az,r)分别为接收卫星轨迹的3维运动参数。传统脉冲雷达的“1步1停”假设在FMCW SAR中不再成立，需要考虑回波时延产生的脉内移动，其回波时延的精确表达式为
τ(t)=Rt(t)+Rr[t+τ(t)]c (3) 其中，c为光速。
以场景中心p0=(x0,y0,z0)为参考点，其对应方位中心时刻的斜距为R0，则有参考时延tdc=2R0/c，参考脉冲宽度为Tpref，将回波与参考信号进行共轭相乘，同时忽略幅值对聚焦结果的影响，可以得到去斜处理后的结果[11]。
3. 星载双基FMCW SAR成像处理
双斜距模型不利于后续的回波特性研究和算法处理，故这里引入一种高阶多项式斜距模型，通过调整多项式的阶数来满足所需的精度，可得4阶等效斜距模型
Req(t)=c[τ(t)−tdc]2≈k0+k1t+k2t2+k3t3+k4t4 (4) 其中，Req(t)为目标点pi=(xi,yi,zi)到雷达等效单程斜距，ki(i=0,1,2,3,4)代表第i阶多项式的系数。值得一提的是，在非线性轨迹的情况下，方位平移不变性不再满足，多项式系数成为方位位置和距离位置的函数，即ki=ki(X,RB)，其中X代表目标方位位置，RB代表目标距离位置。对于低轨星载轨道来说，4阶等效斜距模型足以满足米级分辨率信号处理所需的精度。
3.1 距离维处理
将式(4)代入去剩余视频相位(Residual Video Phase, RVP)项后的回波，表达式可以写为
sr(tr,ta)=rect(tr−tdcTp)wa(ta)⋅exp[−j4πc(γ(tr−tdc)+fc)(4∑i=0kiti)] (5) 其中，wa(ta)是方位窗函数，Tp为发射信号的脉宽，fc为载波频率，γ为调频斜率，将式(5)在tr=0处1阶泰勒展开
Req(tr,ta)≈Req(ta)+R′eq(ta)tr (6) 将式(6)代入回波并整理后得到
sr(tr,ta)=rect(tr−tdcTp)wa(ta)⋅exp[−j4πcfc(Req(ta)+R′eq(ta)tdc)]⋅exp{−j4πcγ(tr−tdc)⋅[Req(ta)+R′eq(ta)(tdc+fcγ)]}⋅exp[−j4πcγ(γ(tr−tdc))2R′eq(ta)] (7) 回波相位第1个指数项包含方位历程信息，第2个指数项与距离相位有关，前两个相位都受到脉内频移的影响，距离和方位项都出现了多普勒调制项，多普勒频移常数项的存在会使目标的位置发生偏移，第3个相位为距离2次脉冲压缩相位。构造2次脉冲压缩函数H1(tr)
H1(tr)=exp[j4πcγ(γ(tr−tdc))2R′0] (8) 其中， 以参考点可求得R′0=R′eq(0)|p=p0。在tr−fa域与2次脉冲压缩信号相乘，并将信号变换到tr−ta域，脉冲压缩后的信号为
sr(tr,ta)=rect(tr−tdcTp)wa(ta)⋅exp[−j4πcfc⋅4∑i=0kaitia]⋅exp[−j4πcγ(tr−tdc)⋅4∑i=0kritia] (9) 将各项系数整理为方位向系数kai(i=0,1,2,3,4)和距离项系数kri(i=0,1,2,3,4)
ka0=k0+k1tdcka1=k1+2k2tdcka2=k2+3k3tdcka3=k3+4k4tdcka4=k4},kr0=k0+k1(tdc+fc/γ)kr1=k1+2k2(tdc+fc/γ)kr2=k2+3k3(tdc+fc/γ)kr3=k3+4k4(tdc+fc/γ)kr4=k4} (10) 先将式(10)做距离快速傅里叶变换(Fast Fourier Transform, FFT)，即tr→fr，接着补偿多普勒中心fa0，对于双基SAR构型来说，其一般不为0，该表达式中fa0=2ka1/λ|p=p0，构造多普勒中心补偿函数
HDPC(ta)=exp(j2πfa0ta) (11) 补偿后的多普勒中心残余为k′a1=ka1−ka1|p=p0，将式(9)与式(11)相乘后，接着变换到方位多普勒域，即作ta→fa的FFT，利用级数反演求解回波信号的方位频谱[12]，推导过程中保留到方位频率fa的4次项，忽略4次以上的高次项，整理后的表达式为
sr(fr,fa)=Tpsinc[Tp(fr+χrcm(fa))]exp[−j2πfrtdc]⋅Wa(ta)exp[−4πλka0+π4ka2λ(fa+2k′a1λ)2+πka316k3a2λ2⋅(fa+2k′a1λ)3+π(9k2a3−4ka2ka4)256k5a2λ3⋅(fa+2k′a1λ)4] (12) 其中，χrcm(fa)中包含回波包络的越距离单元徙动量，影响距离维聚焦。
对式(12)进行距离快速傅里叶逆变换(Inverse FFT, IFFT)，接着对距离徙动项进行校正，这里仅以参考点构造统一的补偿函数，即仅考虑距离的弯曲，而忽略了距离弯曲的空变性，但随着距离带宽的增加和距离幅宽的增大距离维的空变将变得难以忽略，聚焦的效果也会受到影响。构造的统一补偿函数可以表示为
Hrcm(tr,fa)=exp[j2π(tr−tdc)(−γkr12fcka2fa+cγkr28f2ck2a2f2a−c2γkr332f3ck3a2f3a+c3γkr4128f4ck4a2f4a)] (13) 补偿之后对回波进行距离FFT，至此距离维可以实现精确聚焦[13]。距离维处理整体流程如图2所示。
3.2 奇异值分解原理
对于非线性轨迹的双基SAR来说，方位平移不变性不再满足，方位多普勒信息fa和目标方位位置信息X存在一定的耦合，其方位空变不易处理[14]。奇异值分解(SVD)可以有效地分解两者的耦合性，暂时不考虑距离信息，对一个m×n的相位矩阵{\boldsymbol{\varPhi }}({f_{\rm{a}}},X)做SVD处理，可得其分解后的表达式为
{{\boldsymbol{\varPhi}} }({f_{\rm{a}}},X) = \sum\limits_{l = 1}^{\min (m,n)} {{{{\boldsymbol{U}}}_l}({f_{\rm{a}}}){{\boldsymbol{S}}}(l,l){{{\boldsymbol{V}}}_l}(X)} (14) 其中，{{{\boldsymbol{U}}}_l}和{{\boldsymbol{V}}_l}分别为SVD后第l个奇异值{\mathbf{S}}(l,l)所对应的正交向量，其可以看作分别关于{f_{\rm{a}}}和X的函数，整个相位矩阵就可以表示成若干个矩阵的和，且奇异值是按照降序排列。奇异值可以表示一个矩阵的信息，当奇异值越大时，它代表的信息就越多[15]。就这方面来说，其与泰勒展开的作用大体一致，利用多项式或矩阵函数对原问题进行逼近近似，提供一个误差范围内的精确解。
对该回波相位矩阵来说，通常可以通过前几个奇异值来表示，根据表1的仿真参数，分别给出相位矩阵由1个奇异值、2个奇异值和3个奇异值表示的相位误差。由图3可知，2个奇异值表示即可使相位误差远小于\pi /4。
表 1 星载轨道及雷达仿真参数参数名称 参数值 参数名称 参数值 轨道高度 500 km 载频 35.75 GHz 离心率 0.05 信号带宽 150 MHz 下视角 31.5° 脉冲重复频率 4000 Hz 占空比 85 % 采样率 25 MHz 双星间距 10～12 km 合成孔径时间 0.5 s 场景宽度 5 km×5 km 地距分辨率 1.7 m×2.5 m 3.3 方位SVD处理
在3.1节已经完成了距离维的聚焦操作，本节仅考虑方位相位，保留SVD的前两个奇异值，相位信号可以通过SVD操作表示为
\begin{split} {\varPhi _{{\rm{SVD}}}}({f_{\rm{a}}},X) = & - \frac{{4\pi }}{\lambda }{k_{{\rm{a}}0}} + \frac{\pi }{{4{k_{{\rm{a}}2}}\lambda }}{\left( {{f_{\rm{a}}} + \frac{{2{k'_{{\rm{a}}1}}}}{\lambda }} \right)^2} \\ &+ \frac{{\pi {k_{{\rm{a}}3}}}}{{16k_{{\rm{a}}2}^3{\lambda ^2}}}{\left( {{f_{\rm{a}}} + \frac{{2{k'_{{\rm{a}}1}}}}{\lambda }} \right)^3} \\ &+ \frac{{\pi (9k_{{\rm{a}}3}^2 - 4{k_{{\rm{a}}2}}{k_{{\rm{a}}4}})}}{{256k_{{\rm{a}}2}^5{\lambda ^3}}}{\left( {{f_{\rm{a}}} + \frac{{2{k'_{{\rm{a}}1}}}}{\lambda }} \right)^4} \\ \approx &{U_1}({f_{\rm{a}}})S(1,1){V_1}(X) \\ & + {U_2}({f_{\rm{a}}})S(2,2){V_2}(X) \\[-10pt] \end{split} (15) 其中， {U_1}({f_{\rm{a}}}) 和 {U_2}({f_{\rm{a}}}) 是关于{f_{\rm{a}}}的第1个和第2个特征分量，{V_1}(X)和{V_2}(X)是关于X的第1个和第2个特征分量，S(1,1)和S(2,2)是常数奇异值。
首先，对特征分量{U_1}({f_{\rm{a}}})作1次Stolt插值操作，使得{U_1}({f_{\rm{a}}}) \to {U_1}，此时方位频率由原来的{f_{\rm{a}}}变为\chi ({f_{\rm{a}}})，\chi ( \cdot )函数为插值所产生频率的映射关系。插值的目的是消除第1个相位信息随{f_{\rm{a}}}的变化，使其仅与方位位置X有关，从数学的角度理解，插值过程相当于做变量替换的过程。式(15)则可以表示为
\begin{split} {\varPhi _{{\rm{SVD}}}}({f_{\rm{a}}},X) =& {U_1}S(1,1){V_1}(X) \\ & + {U_2}\left( {\chi ({f_{\rm{a}}})} \right)S(2,2){V_2}(X) \end{split} (16) 若相位函数可以仅由1个奇异值分量表示，那么通过第1次SVD插值之后，方位目标即可完成聚焦。对特征值分量{U_2}\left( {F({f_{\rm{a}}})} \right)作关于{f_{\rm{a}}}的展开多项式，各项系数可以通过多项式拟合的数值方法求解得到
\begin{split} {\varPhi }_{{\rm{SVD}}}({f}_{{\rm{a}}},X)\approx \;& {U}_{1}\cdot S(1,1){V}_{1}(X)\\ &+\left[{u}_{0}+{u}_{1}{f}_{{\rm{a}}}+{u}_{2}{f}_{{\rm{a}}}^{2}+{u}_{3}{f}_{{\rm{a}}}^{3}+{u}_{4}{f}_{{\rm{a}}}^{4}\right]\\ &\cdot S(2,2){V}_{2}(X)\\ = &\left[{U}_{1}\cdot S(1,1){V}_{1}(X)+{u}_{0}S(2,2){V}_{2}(X)\right]\\ &+{u}_{1}S(2,2){V}_{2}(X){f}_{{\rm{a}}}\\ &+{u}_{2}S(2,2){V}_{2}(X){f}_{{\rm{a}}}^{2}\\ &+{u}_{3}S(2,2){V}_{2}(X){f}_{{\rm{a}}}^{3}\\ &+{u}_{4}S(2,2){V}_{2}(X){f}_{{\rm{a}}}^{4}\\[-10pt] \end{split} (17) 此时已经消除绝大部分的方位空变，可以近似考虑{f_{\rm{a}}}的3次项及高次相位空变已经被校正，但2次{f_{\rm{a}}}仍不可忽略，构造统一的方位滤波函数对3次项和4次项进行补偿
\begin{split} {H_{{\rm{unity}}}}({f_{\rm{a}}}) =& \exp \left[ - {\rm{j}}{u_3}S(2,2){V_2}({x_0})f_{\rm{a}}^3 \right.\\ & \left.- {\rm{j}}{u_4}S(2,2){V_2}({x_0})f_{\rm{a}}^4 \right] \end{split} (18) 补偿后的方位相位，仍未完全解决方位空变的影响，若对其进行第2次SVD操作可以恰好仅由1个奇异值分量表示，即可通过第2次插值精确补偿，但实际上依然存在两个奇异值分量。根据非线性变标的原理[16,17]，这里在时域引入一个方位变标函数
{H_{{\rm{scale}}}}({t_{\rm{a}}}) = \exp \left( {{\rm{j}}\alpha t_{\rm{a}}^2 + {\rm{j}}\beta t_{\rm{a}}^3} \right) (19) 其目的是通过调整变标因子\alpha 和\beta 的值，来满足方位频域的SVD结果可以仅有1个奇异值矩阵表示。使用驻定相位原理求解{S_{{\rm{SVD}}}}({t_{\rm{a}}},X)的时域表达式为
\begin{split} {S_{{\rm{SVD}}}}({t_{\rm{a}}},X) =& \exp \left[ {\rm{j}}\left( {\varPsi _0}(X) - \frac{{\varPsi _1^2(X)}}{{4{\varPsi _2}(X)}} \right.\right.\\ & \left.\left.- \frac{{\pi {\varPsi _1}(X)}}{{{\varPsi _2}(X)}}{t_{\rm{a}}} - \frac{{{\pi ^2}}}{{{\varPsi _2}(X)}}t_{\rm{a}}^2 \right) \right] \end{split} (20) 其中，{\varPsi }_{0}(X)={U}_{1}\cdot S(1,1){V}_{1}(X)+{u}_{0}S(2,2){V}_{2}(X), {\varPsi _1}(X) = {u_1}S(2,2){V_2}(X), {\varPsi _2}(X) = u{ _2}S(2,2){V_2}(X)。将式(19)与式(20)相乘并作FFT变换到方位频域，经过方位非线性变标后的相位可以表示为
\begin{split} {\varPhi _{{\rm{SVD}}}}({f_{\rm{a}}},X,\alpha ,\beta ) = & {\varphi _0}(X,\alpha ,\beta ) + {\varphi _1}(X,\alpha ,\beta ){f_{\rm{a}}} \\ & + {\varphi _2}(X,\alpha ,\beta )f_{\rm{a}}^2 + {\varphi _3}(X,\alpha ,\beta )f_{\rm{a}}^3\\ \end{split} (21) 其中，{\varphi _0}(X,\alpha ,\beta ), {\varphi _1}(X,\alpha ,\beta ), {\varphi _2}(X,\alpha ,\beta ), {\varphi _3}(X,\alpha ,\beta )为{f_{\rm{a}}}的多项式系数，且均可展开为X的2阶多项式，对应的关于X多项式系数分别为{a_i},{b_i},{c_i},{d_i}(i = 0,1,2)。将式(21)整理后得到
\begin{split} {\varPhi _{{\rm{SVD}}}}({f_{\rm{a}}},X,\alpha ,\beta ) = &{\varphi _0}(X,\alpha ,\beta ) + \left[ {b_0}(\alpha ,\beta ){f_{\rm{a}}} + {c_0}(\alpha ,\beta )\right. \\ & \cdot\left. f_{\rm{a}}^2+ {d_0}(\alpha ,\beta )f_{\rm{a}}^3 \right] + {b_1}(\alpha ,\beta )\\ & \cdot \left[ {{f_{\rm{a}}} + \frac{{{c_1}(\alpha ,\beta )}}{{{b_1}(\alpha ,\beta )}}f_{\rm{a}}^2 + \frac{{{d_1}(\alpha ,\beta )}}{{{b_1}(\alpha ,\beta )}}f_{\rm{a}}^3} \right] X \\ & + {b_2}(\alpha ,\beta )\left[ {f_{\rm{a}}} + \frac{{{c_2}(\alpha ,\beta )}}{{{b_2}(\alpha ,\beta )}}f_{\rm{a}}^2 \right.\\ & \left.+ \frac{{{d_2}(\alpha ,\beta )}}{{{b_2}(\alpha ,\beta )}}f_{\rm{a}}^3 \right]{X^2} \\[-15pt] \end{split} (22) 理想的结果是第2次SVD后方位的频谱相位可以表示为式(23)的形式
{\varPhi _{{\rm{SVD}}}}({f_{\rm{a}}},X,\alpha ,\beta ) = F({f_{\rm{a}}}) \cdot G(X) + I(X) + J({f_{\rm{a}}}) (23) 其中，F({f_{\rm{a}}})G(X)为第2次SVD的唯一奇异值分量，I(X)为常数项，不影响方位的聚焦，J({f_{\rm{a}}})为方位非空变项。当且仅当存在常数\alpha 和\beta 满足，{c_1}(\alpha ,\beta )/ {b_1}(\alpha ,\beta ) \;=\; {c_2}(\alpha ,\beta )/{b_2}(\alpha ,\beta ) \;=\; {\delta _2}(\alpha ,\beta ), {d_1}(\alpha ,\beta )/ {b_1} (\alpha ,\beta ) = {d_2}(\alpha ,\beta )/{b_2}(\alpha ,\beta ) = {\delta _3}(\alpha ,\beta )，将式(22)整理后对照式(23)易得出
\left. \begin{aligned} & F({f_{\rm{a}}}) = {f_{\rm{a}}} + {\delta _2}(\alpha ,\beta )f_{\rm{a}}^2 + {\delta _3}(\alpha ,\beta )f_{\rm{a}}^3 \\ & G(X) = {b_1}(\alpha ,\beta )X + {b_2}(\alpha ,\beta ){X^2}\\ & I(X) = {\varphi _0}(X,\alpha ,\beta ) \\ & J({f_{\rm{a}}}) = {b_0}(\alpha ,\beta ){f_{\rm{a}}} + {c_0}(\alpha ,\beta )f_{\rm{a}}^2 + {d_0}(\alpha ,\beta )f_{\rm{a}}^3 \end{aligned} \right\} (24) 此时对方位相位进行第2次SVD，并构造方位匹配滤波函数补偿方位非空变项J({f_{\rm{a}}})，补偿函数为
{H_{{\rm{match}}}}({f_{\rm{a}}}) = \exp \left[ { - {\rm{j}}J({f_{\rm{a}}})} \right] (25) 将式(23)与式(25)相乘，忽略常数项。此时，进行第2次插值操作，使得F({f_{\rm{a}}}) \to {f''_{\rm{a}}}，再进行方位FFT即可实现方位的精确聚焦[18]。完成两维聚焦处理后的信号为
\begin{split} {s_{\rm{r}}}({f_{\rm{r}}},{t_{\rm{a}}}) = &{{\rm{sinc}}} \left[ {T_{\rm{p}}}\left( {f_{\rm{r}}} + \frac{{2\gamma }}{c}{k_{{\rm{r}}0}} - \frac{{\gamma {k_{{\rm{r}}1}}{k'_{{\rm{a}}1}}}}{{{f_{\rm{c}}}{k_{{\rm{a}}2}}\lambda }} \right.\right.\\ & \left.\left.+ \frac{{{\rm{c}}\gamma {k_{{\rm{r}}2}}{k'_{{\rm{a}}1}}^2}}{{2f_{\rm{c}}^2k_{{\rm{a}}2}^2{\lambda ^2}}} - \frac{{{c^2}\gamma {k_{{\rm{r}}3}}{k'_{{\rm{a}}1}}^3}}{{4f_{\rm{c}}^3k_{{\rm{a}}2}^3{\lambda ^3}}} + \frac{{{c^3}\gamma {k_{{\rm{r}}4}}{k'_{{\rm{a}}1}}^4}}{{8f_{\rm{c}}^4k_{{\rm{a}}2}^4{\lambda ^4}}} \right) \right] \\ &\cdot {{\rm{sinc}}} \left[ {\Delta {f_{\rm{a}}} \left( {{t_{\rm{a}}} + \frac{{{b_1}(\alpha ,\beta )}}{{2\pi }}X + \frac{{{b_2}(\alpha ,\beta )}}{{2\pi }}{X^2}} \right)} \right]\\ & \cdot\exp \left[ { - {\rm{j}}2\pi {f_{\rm{r}}}{t_{{\rm{dc}}}}} \right] \\[-10pt] \end{split} (26) 其中，\Delta {f_{\rm{a}}}为信号的多普勒带宽。
从式(26)可以看出，最终的聚焦图像具有几何形变，在距离和方位方向均有一定的移动，需要进行几何形变的校正。其中距离向的形变是由于脉内频移和非线性轨迹所共同引起的，会使同一距离单元的目标点整体平移，方位向的形变是由于方位的变标因子决定的。方位维处理的时频分布图及流程图如图4所示。
其中，A, B, C分别为同一距离单元，不同方位位置的3个目标点。由图4可知，第1次SVD插值处理补偿了第1个奇异值分量的方位相位空变，其在整体空变中具有较大比重，使得第2个奇异值分量3次及以上相位项的空变可以忽略，可以经过统一滤波函数将时频曲线校正为直线。接着通过在时域引入变标函数，去除了2次相位项的方位空变，使3个点具有共同的时频斜率[19,20]，经过第2次多普勒插值处理，完全处理方位空变相位，仅剩余1次相位项，表明方位的精确聚焦。
4. 仿真验证
本节对所提成像算法的有效性进行验证，星载双基FMCW SAR仿真几何模型如图1所示，其具体的星载轨道及雷达仿真参数见表1，系统工作在条带模式。
星载仿真数据来源于STK仿真软件，仿真场景中点目标几何分布如图5所示，点目标等经纬度间隔分布({\rm{PT}}1 \sim {\rm{PT}}9)，间距约2 km，其中PT5(O)为参考点。采用本文算法对距离维空变的校正结果如图6所示，其中图6(a)为中心距离单元距离维去斜后的包络，可以明显看出距离徙动严重，经过距离徙动校正之后，距离包络已完全校直，见图6(b)。
方位第1次SVD处理后，点目标PT4, PT5和PT6成像结果如图7所示。场景中心点目标已经基本聚焦，但非中心点依然存在较为明显的方位空变，表明2次多普勒项仍然存在，需要进行第2次SVD并脉冲压缩处理。方位第2次SVD处理后，点目标PT4, PT5和PT6成像结果如图8所示，对比图7和图8，边缘点目标副瓣明显降低，方位空变2次相位得到补偿，表明方位也已完全聚焦。点目标聚焦性能评估如表2所示。
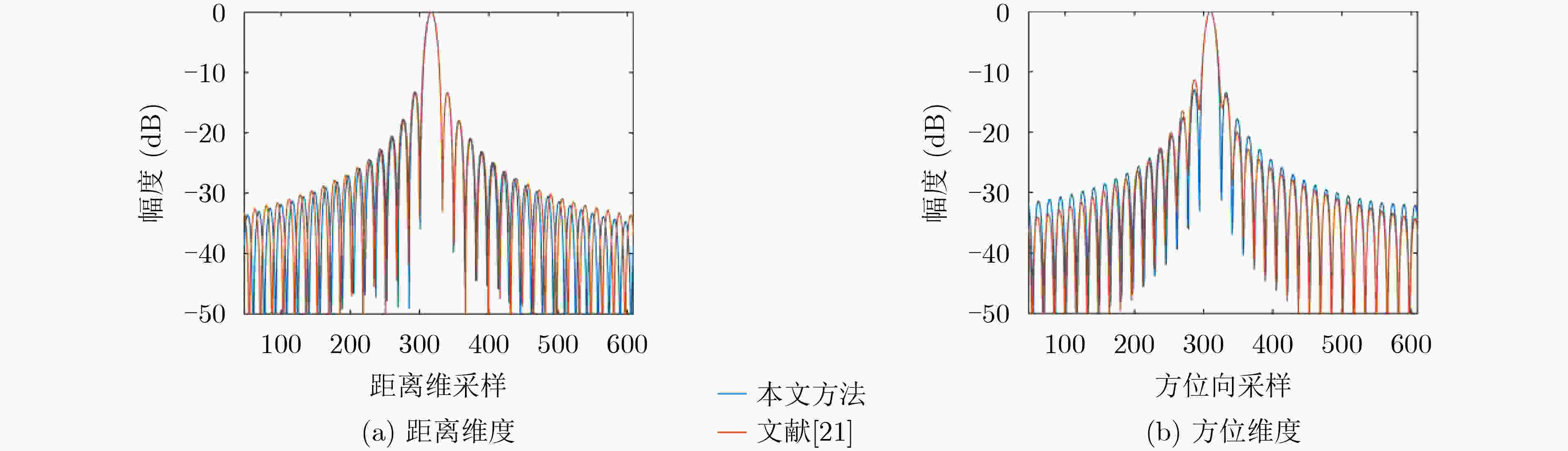
表 2 点目标聚焦性能评估(dB)目标点 PSLR ISLR 距离 方位 距离 方位 PT1 –13.0384 –13.3730 –9.5939 –10.2401 PT4 –13.1874 –13.3809 –9.5523 –10.4050 PT5 –13.1452 –12.8488 –9.5117 –9.9738 PT6 –13.1879 –13.3270 –9.5602 –10.4058 采用本文方法和文献[21]分别对该场景点目标PT1进行成像对比，图9为本文方法和文献[21]对点目标PT1成像的2维采样图。文献[21]采用Keystone变换校正距离徙动项，在多普勒域以参考点构建弯曲校正补偿表达式和统一去斜函数处理方位空变。从图9可以看出文献[21]聚焦的边缘点方位空变仍然存在，方位旁瓣较高；本文方法在距离维和方位维均有不错的聚焦效果。
采用面目标场景对本文算法进行验证，场景大小为5 km \times 5 km，模拟回波仿真采用同心圆算法，大大提高了仿真效率，成像处理结果通过2维插值处理实现几何形变的校正，仿真结果如图10所示。
5. 结束语
本文根据低轨星载双基FMCW SAR的运动形式，建立了几何模型和斜距模型，并对FMCW SAR的回波信号进行整理分析，在距离维进行距离徙动矫正，方位维采用两次SVD处理去除方位空变。通过采用高阶多项式等效双基斜距的方式，大大降低了2维频谱的复杂度，并通过数值方法进行方位拟合和插值操作，完成低轨星载双基SAR的2维聚焦成像。仿真结果验证了本方法的有效性。
-
表 1 星载轨道及雷达仿真参数
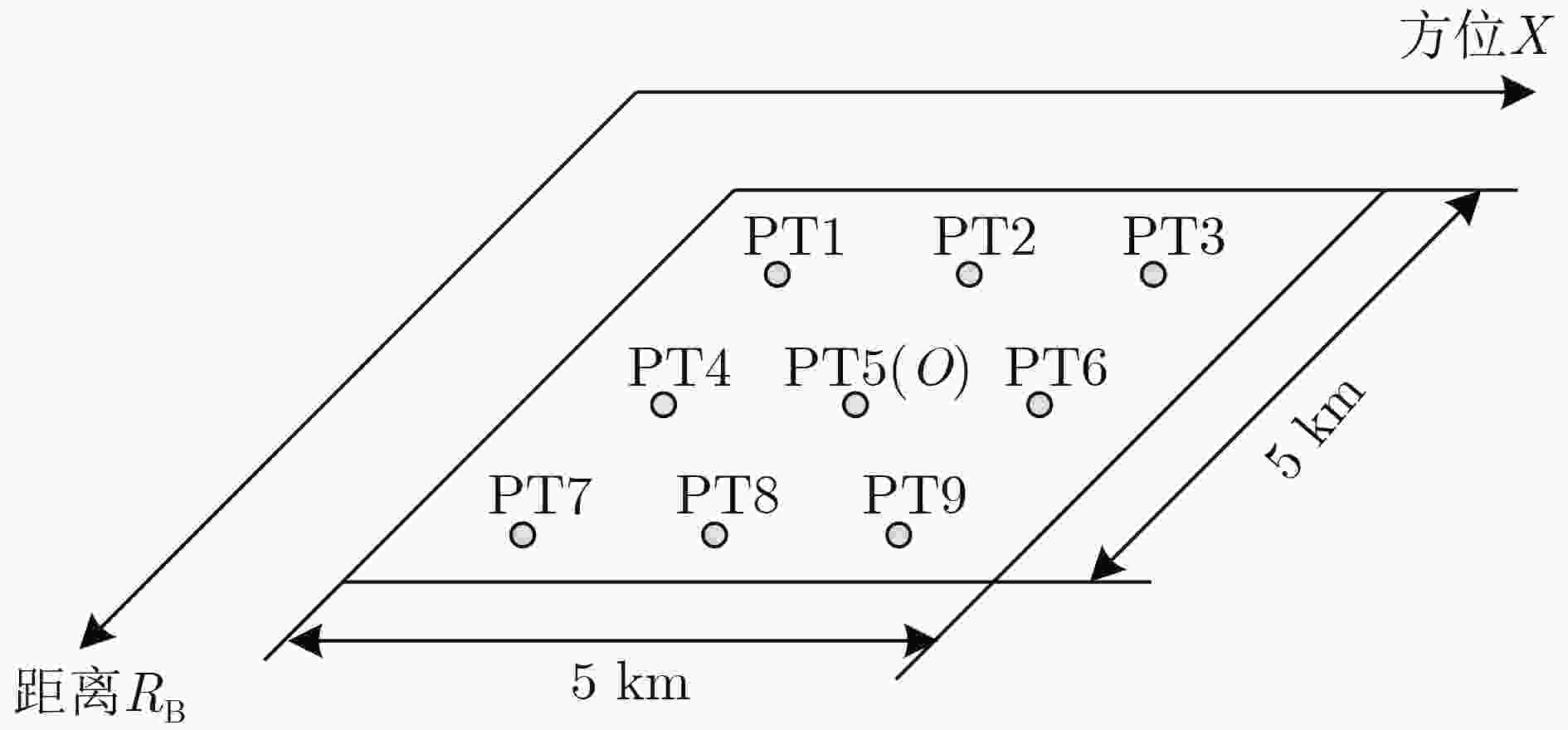
参数名称 参数值 参数名称 参数值 轨道高度 500 km 载频 35.75 GHz 离心率 0.05 信号带宽 150 MHz 下视角 31.5° 脉冲重复频率 4000 Hz 占空比 85 % 采样率 25 MHz 双星间距 10～12 km 合成孔径时间 0.5 s 场景宽度 5 km×5 km 地距分辨率 1.7 m×2.5 m 
下载: 导出CSV
表 2 点目标聚焦性能评估(dB)
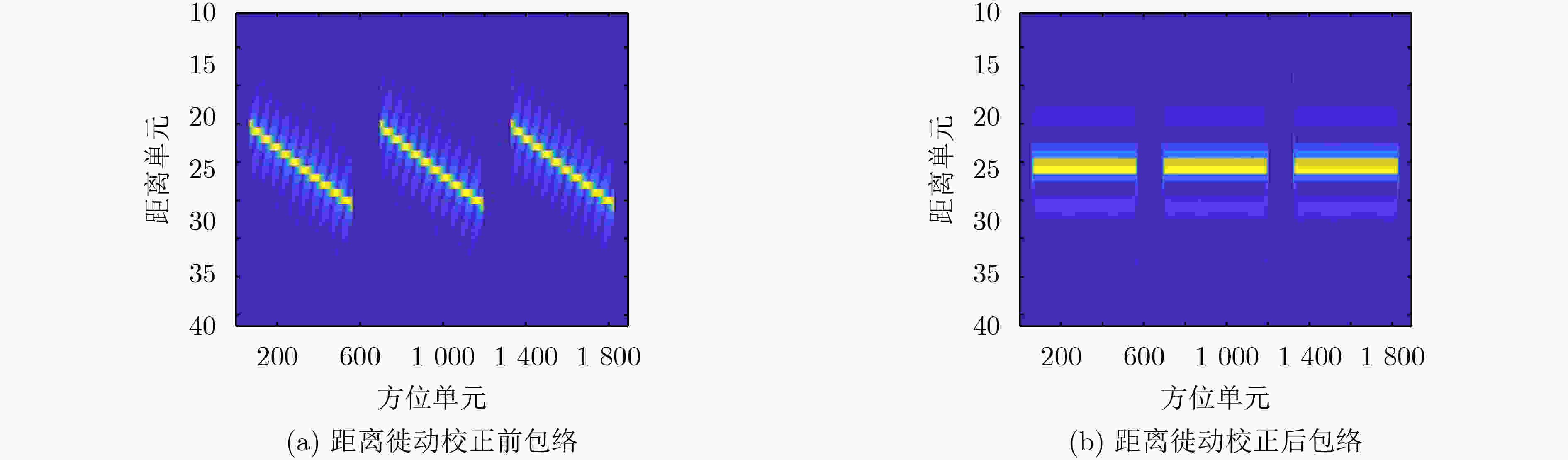
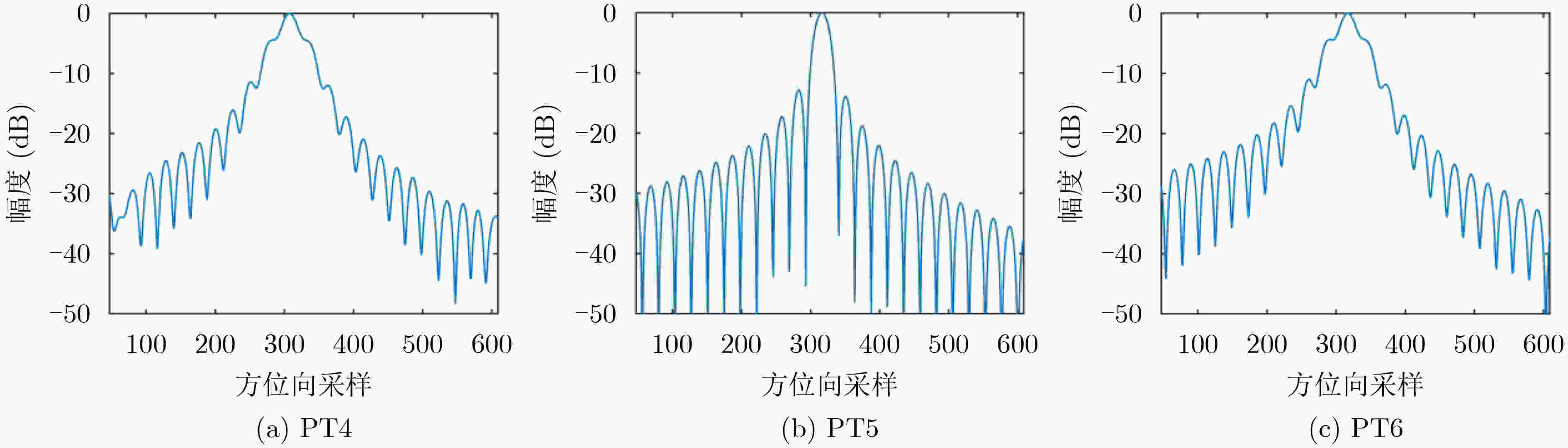
目标点 PSLR ISLR 距离 方位 距离 方位 PT1 –13.0384 –13.3730 –9.5939 –10.2401 PT4 –13.1874 –13.3809 –9.5523 –10.4050 PT5 –13.1452 –12.8488 –9.5117 –9.9738 PT6 –13.1879 –13.3270 –9.5602 –10.4058
下载: 导出CSV
-
[1] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 123–182.BAO Zheng, XING Mengdao, and WANG Tong. Radar Image Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 123–182. [2] LOFFELD O, NIES H, PETERS V, et al. Models and useful relations for bistatic SAR processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10): 2031–2038. doi: 10.1109/TGRS.2004.835295 [3] NEO Y L, WONG F H, and CUMMING I G. Processing of azimuth-invariant bistatic SAR data using the range Doppler algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 14–21. doi: 10.1109/TGRS.2007.909090 [4] LIU Wenkang, SUN Guangcai, XING Mengdao, et al. Focusing of MEO SAR data based on principle of optimal imaging coordinate system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(8): 5477–5489. doi: 10.1109/TGRS.2020.2966581 [5] LIU Wenkang, SUN Guangcai, XING Mengdao, et al. 2-D beam steering method for squinted high-orbit SAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(6): 4827–4840. doi: 10.1109/TGRS.2020.3015904 [6] ZHANG Yixin and FANG Lili. Imaging for bistatic airborne frequency modulated continuous wave SAR[C]. 2019 International Conference on Electronic Engineering and Informatics, Nanjing, China, 2019: 155–158. [7] BIE Bowen, QUAN Yinghui, LIU Wenkang, et al. A modified range model and doppler resampling based imaging algorithm for high squint SAR on maneuvering platforms[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(11): 1923–1927. doi: 10.1109/LGRS.2019.2959660 [8] 李根, 马彦恒, 侯建强, 等. 基于Keystone变换和扰动重采样的机动平台大斜视SAR成像方法[J]. 电子与信息学报, 2020, 42(10): 2485–2492. doi: 10.11999/JEIT190831LI Gen, MA Yanheng, HOU Jianqiang, et al. Maneuvering platform high-squint SAR imaging method based on keystone transform and perturbation resampling[J]. Journal of Electronics &Information Technology, 2020, 42(10): 2485–2492. doi: 10.11999/JEIT190831 [9] CHEN Jianlai, SUN Guangcai, WANG Yong, et al. A TSVD-NCS algorithm in range-doppler domain for geosynchronous synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(11): 1631–1635. doi: 10.1109/LGRS.2016.2599224 [10] LIU Yue, DENG Yunkai, WANG R, et al. Bistatic FMCW SAR signal model and imaging approach[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 2017–2028. doi: 10.1109/TAES.2013.6558035 [11] 梁毅, 王虹现, 邢孟道, 等. 基于FMCW的大斜视SAR成像研究[J]. 电子与信息学报, 2009, 31(4): 776–780. doi: 10.3724/SP.J.1146.2007.01851LIANG Yi, WANG Hongxian, XING Mengdao, et al. Imaging study of high squint SAR based on FMCW[J]. Journal of Electronics &Information Technology, 2009, 31(4): 776–780. doi: 10.3724/SP.J.1146.2007.01851 [12] NEO Y L, WONG F, and CUMMING I G. A two-dimensional spectrum for bistatic SAR processing using series reversion[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(1): 93–96. doi: 10.1109/LGRS.2006.885862 [13] 王开民. 调频连续波无人机SAR动目标成像研究[D]. [硕士论文], 电子科技大学, 2020.WANG Kaimin. Research on moving target imaging of FMCW SAR mounted on unmanned aerial vehicle[D]. [Master dissertation], University of Electronic Science and Technology, 2020. [14] BIE Bowen, QUAN Yinghui, XU Kaijie, et al. High-speed maneuvering platform SAR imaging with optimal beam steering control[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5216012. doi: 10.1109/TGRS.2021.3121427 [15] 游冬, 孙光才, 李亚超, 等. 地球同步轨道SAR两维奇异值分解成像方法[J]. 系统工程与电子技术, 2018, 40(10): 2200–2206. doi: 10.3969/j.issn.1001-506X.2018.10.07YOU Dong, SUN Guangcai, LI Yachao, et al. Two-dimension SVD imaging method for GEO SAR[J]. Systems Engineering and Electronics, 2018, 40(10): 2200–2206. doi: 10.3969/j.issn.1001-506X.2018.10.07 [16] TANG Wanru, HUANG Bang, ZHANG Shunsheng, et al. Focusing of spaceborne SAR data using the improved nonlinear chirp scaling algorithm[C]. 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, USA, 2020: 6555–6558. [17] SUN Guangcai, CHEN Jianlai, YANG Jun, et al. A 2-D space-variant chirp scaling algorithm for GEO SAR[C]. The 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 2014: 1–4. [18] XIONG Yi, LIANG Buge, YU Hanwen, et al. Processing of bistatic SAR data with nonlinear trajectory using a controlled-SVD algorithm[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 5750–5759. doi: 10.1109/JSTARS.2021.3084619 [19] SUN Guangcai, XING Mengdao, WANG Yong, et al. A 2-D space-variant chirp scaling algorithm based on the RCM equalization and subband synthesis to process geosynchronous SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 4868–4880. doi: 10.1109/TGRS.2013.2285721 [20] FENG Lipeng, WANG Hui, ZHENG Shichao, et al. Spaceborne bistatic FMCW SAR imaging method based on FS algorithm[C]. The 2021 2nd China International SAR Symposium, Shanghai, China, 2021: 1–5. [21] MEI Haiwen, LI Yachao, XING Mengdao, et al. A frequency-domain imaging algorithm for translational variant bistatic forward-looking SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(3): 1502–1515. doi: 10.1109/TGRS.2019.2943743 -
计量
- 文章访问数: 383
- HTML全文浏览量: 199
- PDF下载量: 70
- 被引次数: 0
下载:
