Efficient Grouping Secure Aggregation Method Based on Binary Tree
-
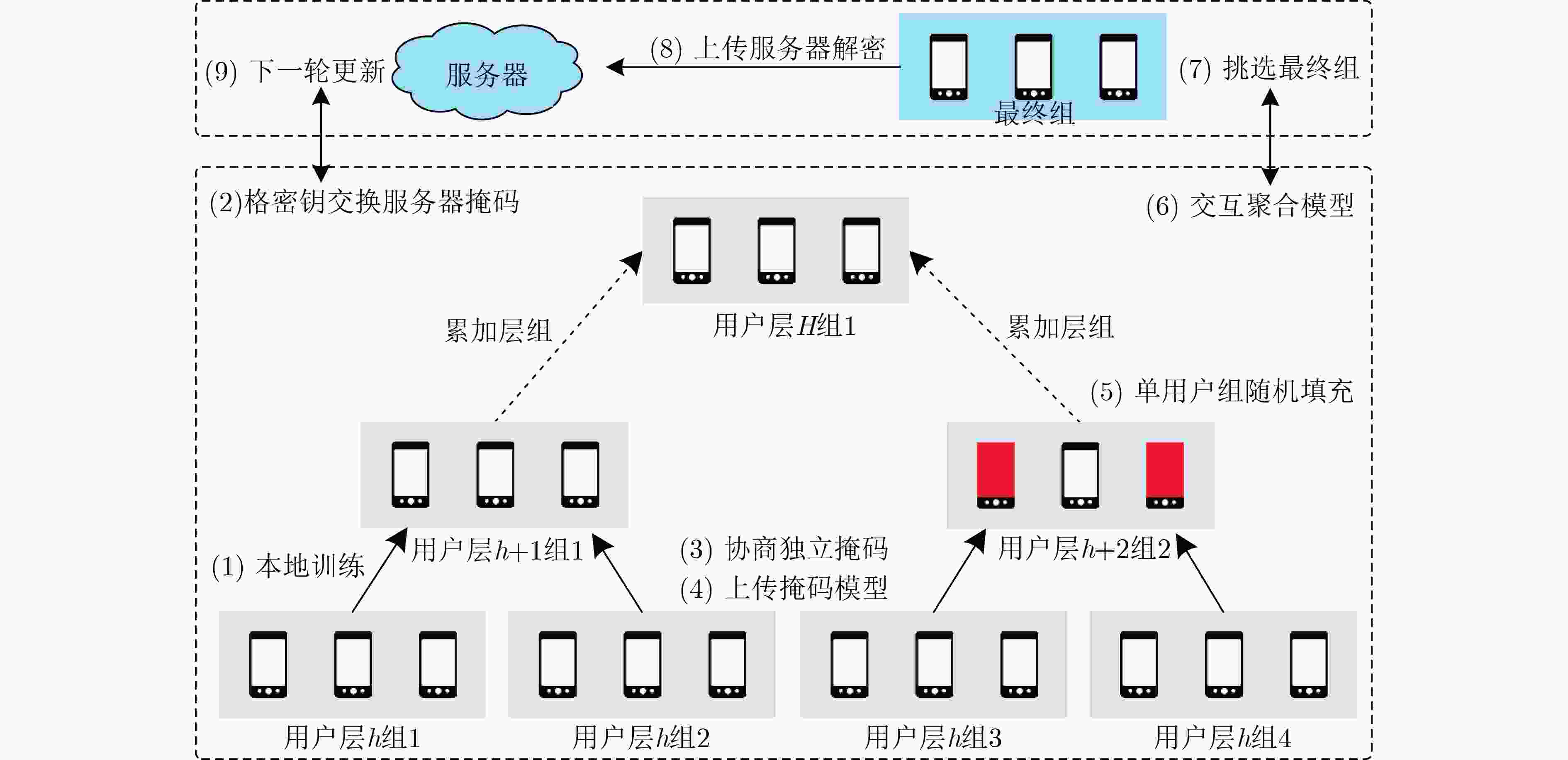
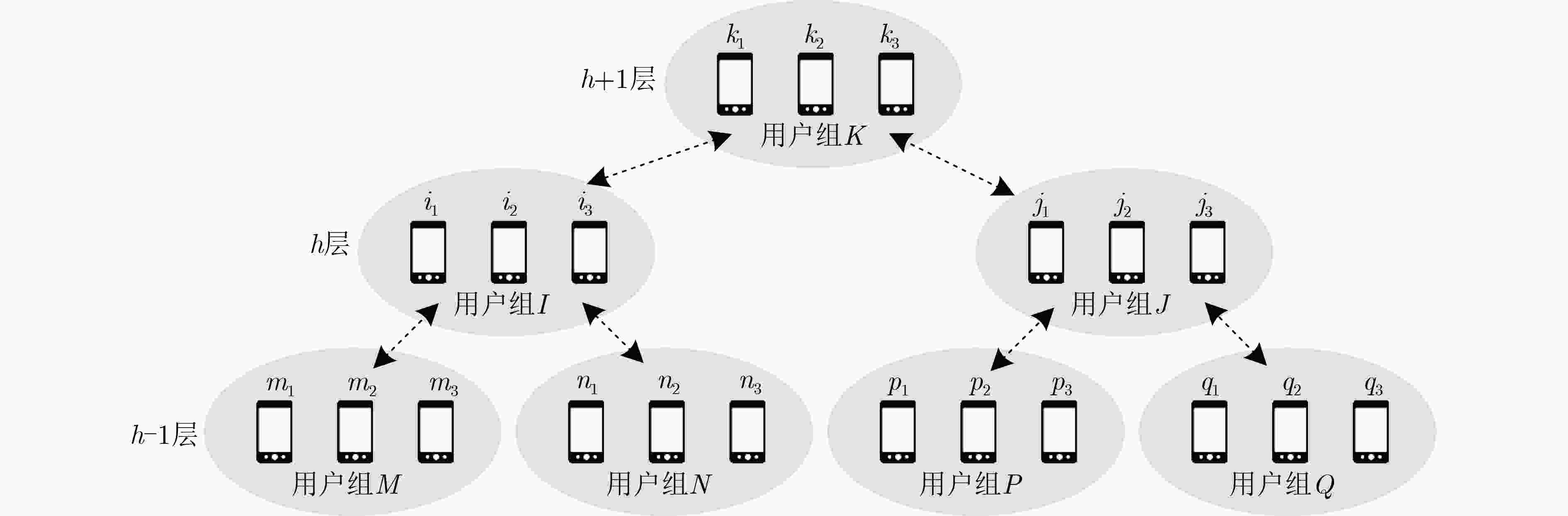
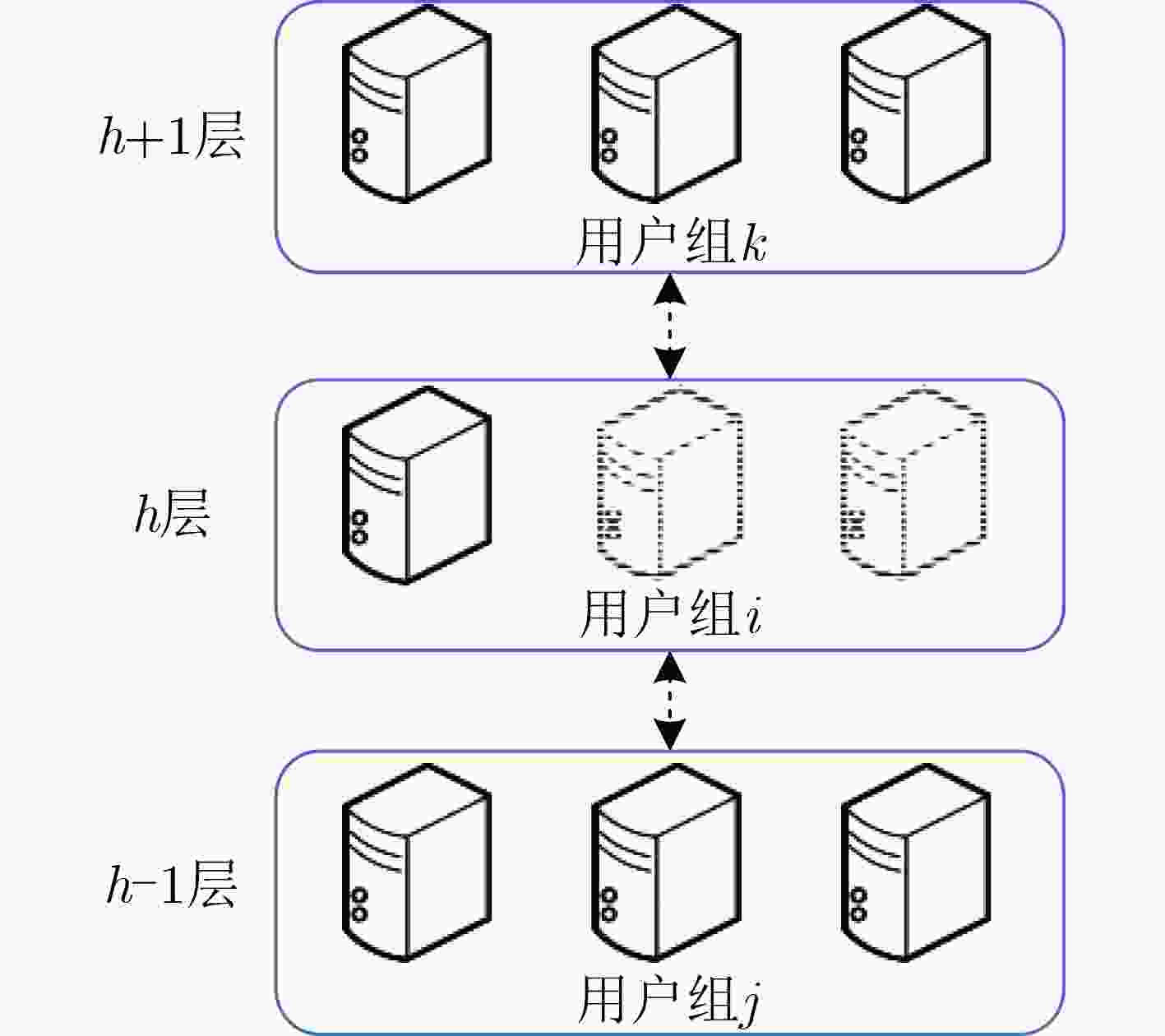
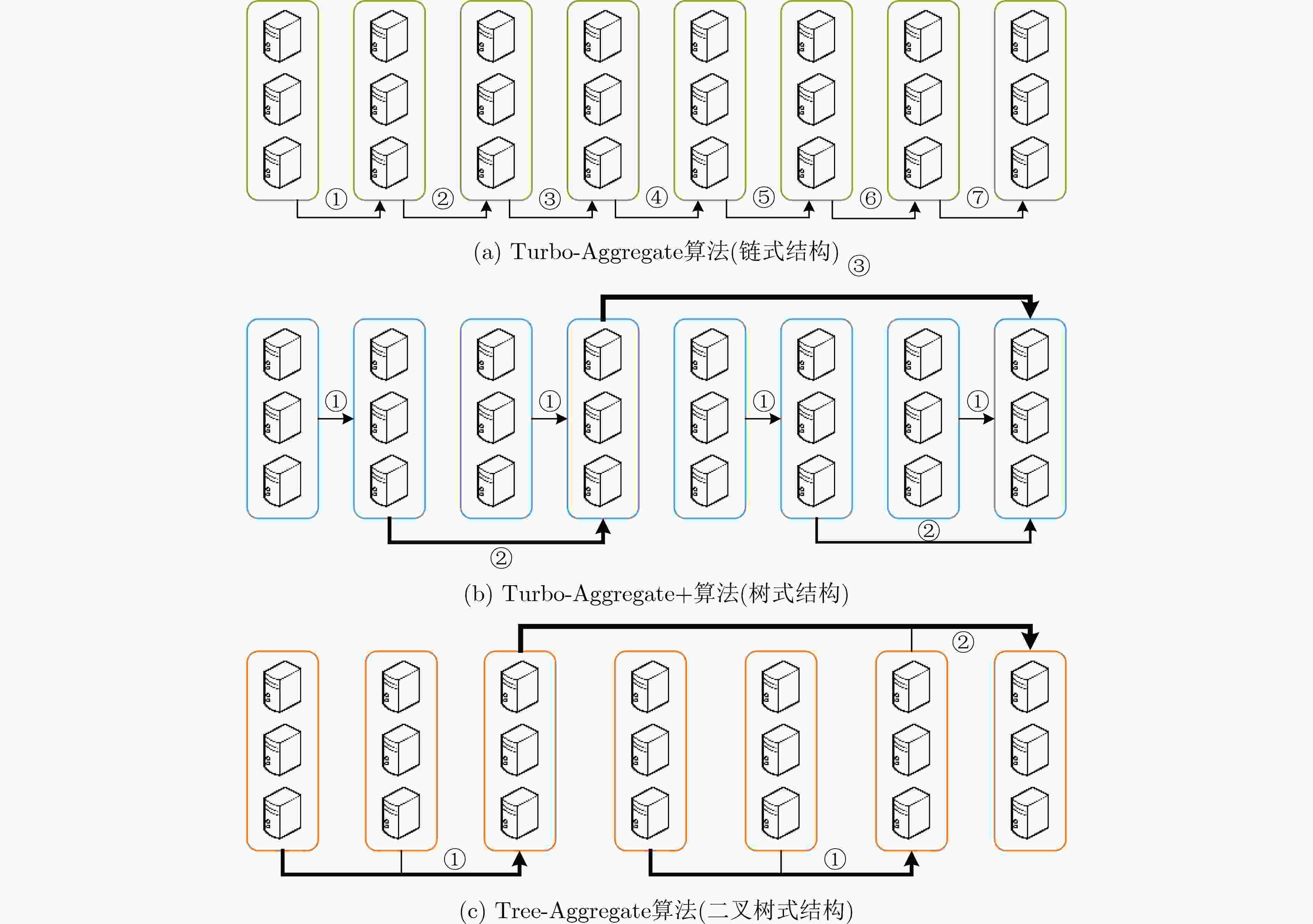
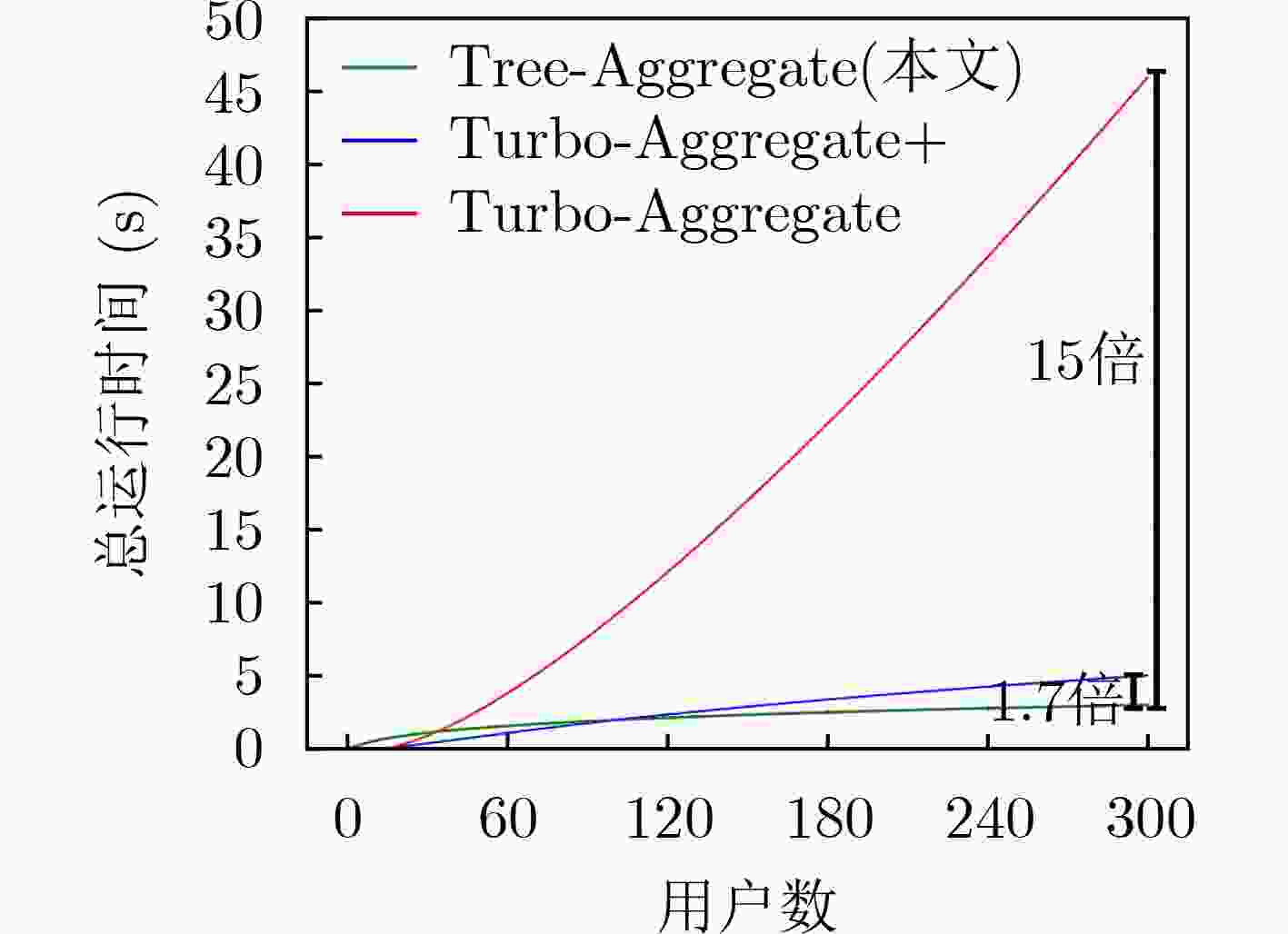
摘要: 安全聚合是联邦学习安全共享过程中确保本地模型聚合安全性和隐私性的关键环节。然而,现有方法存在计算开销大、公平机制差、隐私泄露、无法抗量子攻击等问题。为此,该文提出一种基于二叉树的高效分组安全聚合方法(Tree-Aggregate)。首先,基于二叉树构建用户分组安全通信协议将计算开销从$O\left( {N{\text{l}}{{\text{g}}^2}{\text{lg}}N{\text{lglglg}}N} \right)$降到$O\left( {\lg N{\text{lg}}N} \right)$量级,并通过均匀分摊机制保证了用户计算开销的公平性;然后,提出一种分组不均衡场景下的随机填充算法,解决单一用户引起的隐私泄露问题。最后,该文通过融入格密钥交换协议,为Tree-Aggregate方法增加了抗量子攻击的能力。通过理论分析,Tree-Aggregate将计算开销的增长速率由线性级别变为对数级别,并通过实验对比分析表明,当用户数量N ≥300时计算开销相较于现有方法减小了近15倍。Abstract: Secure aggregation is a key step to ensure the security and privacy of local model aggregation in federated learning security sharing. However, the existing methods have many problems, such as high computational overhead, poor fairness mechanism, privacy disclosure, and inability to resist quantum attack. Therefore, Tree-Aggregate, an efficient grouping secure aggregation method based on binary tree is proposed in this paper. Firstly, the binary tree based user group security communication protocol can reduce the computation cost from $\textstyle O\left( {N{\text{l}}{{\text{g}}^2}{\text{lg}}N{\text{lglglg}}N} \right)$ to $\textstyle O\left( {{\text{lg}}N{\text{lg}}N} \right)$ magnitude and ensure the fairness of the computation cost through the uniform allocation mechanism. Then, a random padding algorithm is proposed to solve the privacy leakage problem caused by a single user. Finally, the anti-quantum attack capability of tree-aggregate method is improved by incorporating lattice-key exchange protocol. Through theoretical analysis, tree-aggregate can change the growth rate of computation cost from linear level to logarithmic level, and through experimental comparative analysis, when the number of users N ≥300, computation cost is reduced by nearly 15 times compared with existing methods.
-
Key words:
- Federated learning /
- Security aggregation /
- Grouping topology /
- Fairness
-
表 1 主要参数说明
参数 定义 N 用户总数量 L 用户分组 H 用户分层 ${N_l}$ 位于l 组中的用户数量 $u$ 服务器掩码 $r$ 独立掩码 s 局部聚合模型 表 2 计算开销对比
方法 计算开销 文献[4] $O\left( {mN{\text{lo}}{{\text{g}}^2}{\text{log}}N{\text{logloglog}}N} \right)$ 文献 [8] $O\left( {m{N^2}} \right)$ 文献[12] $O\left( {mN{\text{log}}N + N{\text{lo}}{{\text{g}}^2}N} \right)$ 文献[13] $O\left( {mN{\text{log}}N} \right)$ 文献[14] $O\left( {mN} \right)$ 本文 $O\left( {m{\text{log}}N{\text{log}}N} \right)$ -
[1] MCMAHAN B, MOORE E, RAMAGE D, et al. Communication-efficient learning of deep networks from decentralized data[C]. The 20th International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, USA, 2017: 1273–1282. [2] IMTEAJ A, THAKKER U, WANG Shiqiang, et al. A survey on federated learning for resource-constrained IoT devices[J]. IEEE Internet of Things Journal, 2022, 9(1): 1–24. doi: 10.1109/jiot.2021.3095077 [3] 周传鑫, 孙奕, 汪德刚, 等. 联邦学习研究综述[J]. 网络与信息安全学报, 2021, 7(5): 77–92. doi: 10.11959/j.issn.2096-109x.2021056ZHOU Chuanxin, SUN Yi, WANG Degang, et al. Survey of federated learning research[J]. Chinese Journal of Network and Information Security, 2021, 7(5): 77–92. doi: 10.11959/j.issn.2096-109x.2021056 [4] SO J, GÜLER B, and AVESTIMEHR A S. Turbo-aggregate: Breaking the quadratic aggregation barrier in secure federated learning[J]. IEEE Journal on Selected Areas in Information Theory, 2021, 2(1): 479–489. doi: 10.1109/jsait.2021.3054610 [5] SYTA E, JOVANOVIC P, KOGIAS E K, et al. Scalable bias-resistant distributed randomness[C]. The 38th IEEE Symposium on Security and Privacy (SP), San Jose, USA, 2017: 444–460. [6] DIFFIE W and HELLMAN M. New directions in cryptography[J]. IEEE Transactions on Information Theory, 1976, 22(6): 644–654. doi: 10.1109/tit.1976.1055638 [7] BONAWITZ K, IVANOV V, KREUTER B, et al. Practical secure aggregation for federated learning on user-held data[C]. The 30th Annual Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain, 2016: 1–5. [8] BONAWITZ K, IVANOV V, KREUTER B, et al. Practical secure aggregation for privacy-preserving machine learning[C]. The 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, USA, 2017: 1175–1191. [9] MONZ T, NIGG D, MARTINEZ E A, et al. Realization of a scalable Shor algorithm[J]. Science, 2016, 351(6277): 1068–1070. doi: 10.1126/science.aad9480 [10] ALKIM E, DUCAS L, PÖPPELMANN T, et al. Post-quantum key exchange: A new hope[C]. The 25th USENIX Conference on Security Symposium, Austin, USA, 2016: 327–343. [11] FRANCESCHETTI M and MINERO P. Elements of information theory for networked control systems[M]. COMO G, BERNHARDSSON B, and RANTZER A. Information and Control in Networks. Cham: Springer, 2014: 3–37. [12] BELL J H, BONAWITZ K A, GASCÓN A, et al. Secure single-server aggregation with (poly)logarithmic overhead[C]. The 2020 ACM SIGSAC Conference on Computer and Communications Security, New York, USA, 2020: 1253–1269. [13] CHOI B, SOHN J, HAN Dongjun, et al. Communication-computation efficient secure aggregation for federated learning[J]. arXiv: 2012.05433, 2020. [14] FEREIDOONI H, MARCHAL S, MIETTINEN M, et al. SAFELearn: Secure aggregation for private federated learning[C]. 2021 IEEE Security and Privacy Workshops (SPW), San Francisco, USA, 2021: 56–62. [15] HE Chaoyang, ANNAVARAM M, and AVESTIMEHR S. Group knowledge transfer: Collaborative training of large CNNs on the edge[J]. arXiv: 2007.14513, 2020. [16] HE Chaoyang, LI Songze, SO J, et al. FedML: A research library and benchmark for federated machine learning[J]. arXiv: 2007.13518, 2020. [17] DALCÍN L, PAZ R, and STORTI M. MPI for python[J]. Journal of Parallel and Distributed Computing, 2005, 65(9): 1108–1115. doi: 10.1016/j.jpdc.2005.03.010 -





 下载:
下载:


 下载:
下载:
