1.   引言

认证加密算法广泛应用于各类安全系统中^[1]，是一类兼具消息认证与数据加密功能的密码算法。认证加密算法一般包括加密算法$\mathcal{E}$与解密算法$\mathcal{D}$。加密算法输入密钥$K$、Nonce$N$、相关数据$A$、明文$M$，输出密文$C$、认证码$T$

解密算法$\mathcal{D}$输入密钥$K$、Nonce$N$、相关数据$A$、密文$C$、认证码$T$，认证通过时输出明文$M$，否则输出$\bot$

2014年，国际密码研究协会发起凯撒(Competition on Authenticated Encryption: Security, Apllicability, and Robustness, CAESAR)竞赛^[2]，面向全球密码工作者征集认证加密算法，最终于2018年公布了7个优胜算法，包括MORUS, ACORN, AEGIS, Ascon, COLM, Deoxys, OCB。2018年，美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)发起征集兼具认证与加密功能的轻量级密码算法的进程^[3]，并于2021年公布了10个优胜算法。随着各种新型认证加密算法的提出，其安全性研究成为当前的热点问题^[4-7]。

以往的安全分析往往依赖手工推导，1994年，Matsui^[8]提出了分支定界搜索算法来搜索最优差分链，这是一种强有力的分析工具，拉开了自动化分析密码算法安全性的序幕^[9-12]。2014年，Sun等人^[13]建立混合整数线性规划(Mixed-Integer Linear Programming, MILP)模型刻画密码算法的差分性质，并利用Gurobi求解器求解MILP模型，以此来搜索最优差分链。为了提高MILP模型的求解速度，Zhou等人^[14]针对沙盒置换网络(Sbox Permutation Net, SPN)结构的分组密码算法提出了分而治之策略，有效地提高了差分\线性链的搜索效率。

作为CAESAR竞赛的优胜算法之一，认证加密算法MORUS由Wu等人^[15]设计提出，遵循了流密码算法的设计思路，根据参数设置分为3个版本MORUS-640-128,MORUS-1280-128,MORUS-1280-256。自提出以来，MORUS的安全性分析得到了广泛的研究，张沛等人^[16]从完全性和差分扩散性两个角度对MORUS-640的初始化阶段进行了研究，给出了MORUS初始化阶段的差分推导规则，并对简化版MORUS进行了差分-区分攻击，施泰荣等人^[17]结合中间相遇思想研究了MORUS算法在故障模型中的差分性质。

现有工作对MORUS算法的差分分析仍有较大改进空间，本文主要基于MILP自动搜索技术研究了MORUS算法初始化阶段的差分性质。首先给出一个改进的差分推导规则，相较张沛等人^[16]的工作，在初始化阶段步数较大时可以找到更好的差分链。进而，给出了刻画MORUS初始化阶段差分性质的MILP模型，当初始化阶段步数较大时，MILP模型无法在有限时间内求解，本文针对MORUS初始化阶段的结构特点给出了分而治之策略，根据$\Delta {\text{IV}}$的重量及取值，将MILP模型划分为多个子模型，并证明了其中大部分模型具有等价性，不需要对这一部分子模型进行求解，从而得到了初始化阶段1～6步状态更新的最优差分链。最后，根据得到的差分链给出了MORUS的差分-区分攻击。之前的工作^[16,17]只分析了MORUS-640的差分性质，本文对MORUS的所有版本均给出了差分分析结果，且较之前的结果有较大提升。

2.   认证加密算法MORUS

MORUS算法^[15]包括3种参数设置：MORUS-640-128, MORUS-1280-128, MORUS-1280-256，表1给出了MORUS的具体参数设置。

表 1  MORUS的参数设置(bit)

参数	MORUS-640-128	MORUS-1280-128	MORUS-1280-256
密钥长度	128	128	256
IV长度	128	128	128
状态大小	640	1280	1280
认证码长度	128	128	128

下载: 导出CSV 

| 显示表格

下文用MORUS-640指代MORUS-640-128，用MORUS-1280指代MORUS-1280-128与MORUS-1280-256。在具体介绍MORUS算法之前，先给出符号说明如表2所示。

表 2  符号说明

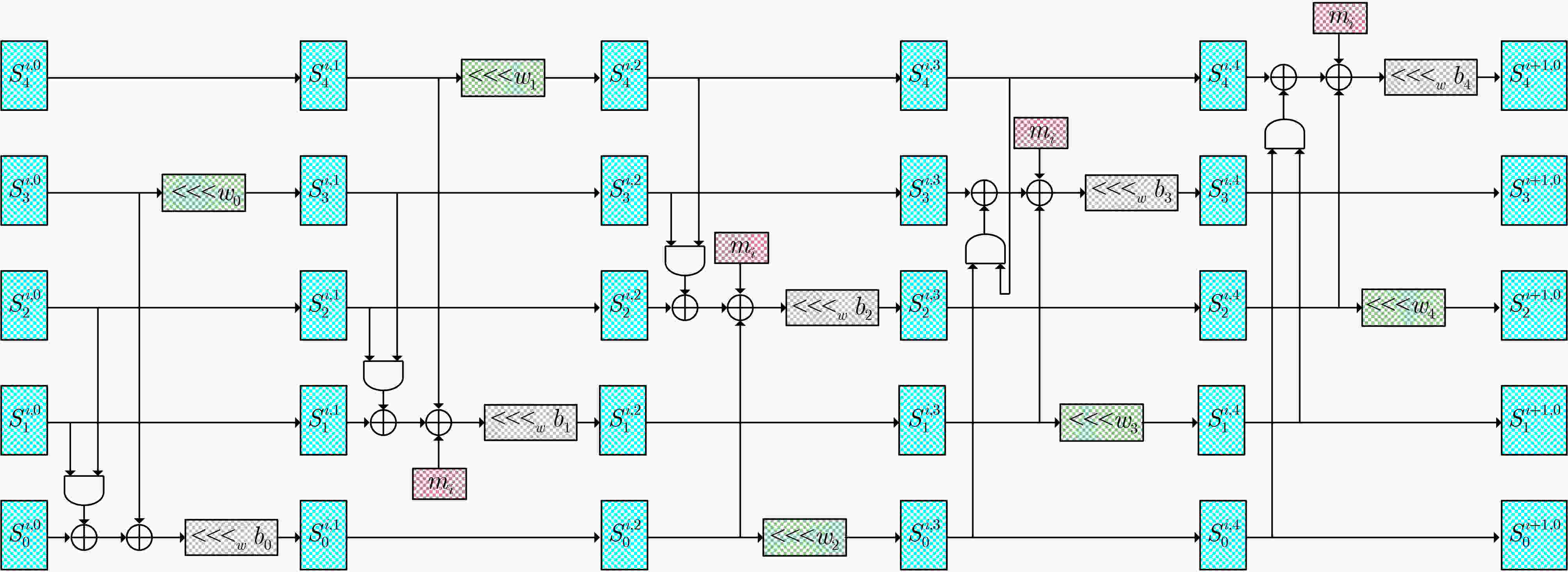
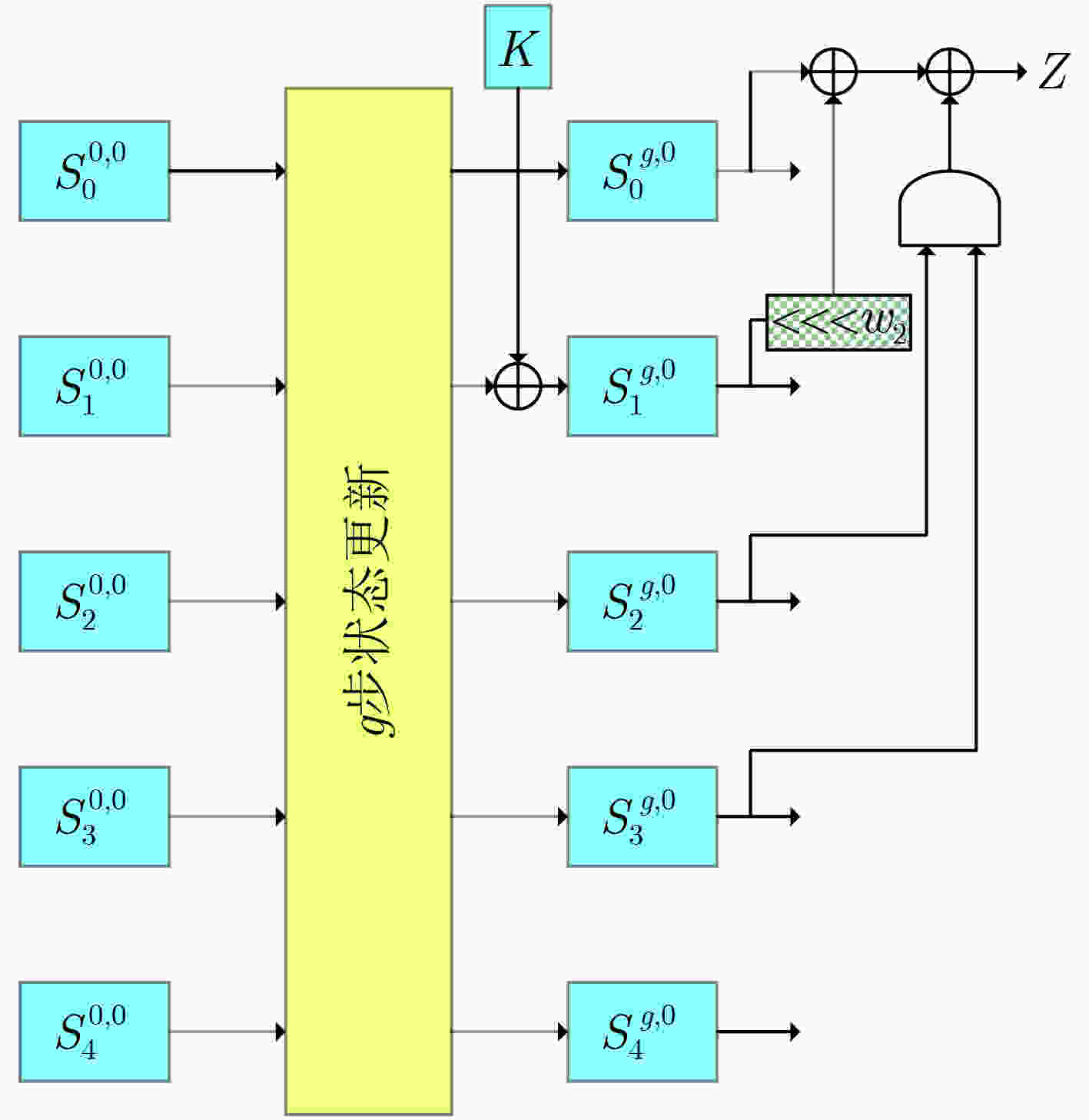
符号	说明
$\oplus$	逐比特异或；
$\&$	逐比特与；
<<<	循环左移；
${0^l}$	$l$ bit 0；
${1^l}$	$l$ bit 1；
${\text{cons}}{{\text{t}}_{\text{0}}}$	$00||01||01||02||03||05||08||0d||15||22||37||59||90||e9||79||62$；
${\text{cons}}{{\text{t}}_{\text{1}}}$	$db||3d||18||55||6d||c2||2f||f1||20||11||31||42||73||b5||28||dd$；
${S^i}$	第$i$步输入状态；
${S^{i,j}}$	第$i$步第$j$轮输入状态；
$S_k^{i,j}$	${S^{i,j}}$第$k$个bit块，对于MORUS-640，每个状态包含5个128 bit块，对于MORUS-1280，每个状态包含5个256 bit块；
$S_{k,l}^{i,j}$	$S_k^{i,j}$的第$l$ bit。

下载: 导出CSV 

| 显示表格

对于$x\;{\rm{bit}}(x = 128,256)$块$X = {X_1}||{X_2}||{X_3}||{X_4}$，其中${X_i}$是$y\;{\rm{bit}}(y = 32,64)$字，${\text{Rot\_}}x{\text{\_}}y(X,b) = ({X_1} < << b)||({X_2} \;<<<\; b)||({X_3} \;<<<\; b)||({X_4} \;<<<\; b)$。MORUS的状态更新函数为${S^{i + 1}} = {\text{StateUpdate}} ({S^i},{m_i})$，状态更新函数包括5轮子函数，图1给出了其具体结构。

图 1  MORUS的状态更新函数

下载: 全尺寸图片 幻灯片

表3给出了状态更新函数中${b_i},{w_i}(i = 0,1,2,3,4)$的取值。

表 3  循环常数

	MORUS-640	MORUS-1280			MORUS-640	MORUS-1280
${b_0}$	5	13		${w_0}$	32	64
${b_1}$	31	46		${w_1}$	64	128
${b_2}$	7	38		${w_2}$	96	192
${b_3}$	22	7		${w_3}$	64	128
${b_4}$	13	4		${w_4}$	32	64

下载: 导出CSV 

| 显示表格

完整的MORUS加密算法包括4个阶段：初始化阶段、相关数据处理阶段、明文处理阶段、认证码生成阶段，下面给出MORUS-5n算法$n = 128, 256$的具体描述：

(1) 初始化阶段。装填密钥$K$与${\rm{IV}}$得到初始状态${S^0}$，对于MORUS-640，令

完成$K$与${\text{IV}}$的装填后，初始化状态经过16步状态更新函数

最后进行密钥加

(2) 相关数据处理阶段。相关数据${\text{AD}}$被分割成$u$个$n$ bit块${\text{AD}} \to {\text{A}}{{\text{D}}_0}||{\text{A}}{{\text{D}}_1}|| \cdots ||{\text{A}}{{\text{D}}_{u - 1}}$，并参与接下来的状态更新

(3) 明文处理阶段。明文$P$被分割成$v$个$n$ bit块$P \to {P_0}||{P_1}|| \cdots ||{P_{v - 1}}$，进行加密与状态更新：对于${\text{ }}i = 0,1, \cdots ,v - 1$

(4) 认证码生成阶段。令${L_1}$,${L_2}$分别为相关数据长度$|{\text{AD}}|$与明文长度$|P|$的64 bit二进制表示，令${\text{tmp}} = {L_1}||{L_2}||{0^{n - 128}}$，${S^{16 + u + v,4}} = {S^{16 + u + v,4}} \oplus {S^{16 + u + v,0}}$，继续进行状态更新

产生认证码

3.   MORUS的差分推导规则

本节针对MORUS算法初始化阶段给出差分推导规则，意在寻找概率较高的差分链。MORUS算法中唯一的非线性操作是逐比特与运算，对于与运算$y = {x_1}\& {x_2}$，假设输入变量差分为$\Delta {x_1}$,$\Delta {x_2}$，则输出差为

根据输入差分的不同，划分为以下4种情况：

(1) $\Delta {x_1} = 0$, $\Delta {x_2} = 0$，则$\Delta y = 0$；

(2) $\Delta {x_1} = 0$, $\Delta {x_2} = 1$，则$\Delta y = {x_1}$；

(3) $\Delta {x_1} = 1$, $\Delta {x_2} = 0$，则$\Delta y = {x_2}$；

(4) $\Delta {x_1} = 1$, $\Delta {x_2} = 1$，则$\Delta y = {x_1} \oplus {x_2} \oplus 1$。

从情况(2)—情况(4)中可以看到$\Delta y$的取值是与输入变量的值有关的，当输入变量的值已知时，$\Delta y$的值以概率1确定，当输入变量的值未知时，$\Delta y$以概率${1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}$取0，以概率${1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}$取1(事实上，MORUS初始化阶段仅第1步中的部分内部状态是已知的)。据此，本文将以上情况分为两类：

A：$\Delta y$以概率1取定值；

B：$\Delta y$以概率${1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}$取0，以概率${1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}$取1。

对于MORUS状态更新函数中的任意内部状态差分$\Delta S_k^{i,j}$，本文称$\Delta S_k^{i,j}$中bit 1的数量为该内部状态差分的重量，记为$|\Delta S_k^{i,j}|$。直观地，在差分推导过程中，为了提高差分链的概率，希望内部状态差分的重量尽可能小。为了方便描述本文暂时忽略所有移位操作，这对分析不会产生任何实质影响。

首先看第$i$步状态更新函数中第1轮的与门$Y_l^{i,0} = S_{0,l}^{i,0} \oplus S_{1,l}^{i,0}\& S_{2,l}^{i,0} \oplus S_{3,l}^{i,0}$，为了研究其输出差分$\Delta Y_l^{i,0}$的取值将会产生的影响，观察$Y_l^{i,0}$直接参与的所有运算：1个异或$Y_l^{i,0} \oplus S_{2,l}^{i,2} \oplus S_{3,l}^{i,2}\& S_{4,l}^{i,2}$，2个与门$Y_l^{i,0}\& S_{4,l}^{i,3}$, $Y_l^{i,0}\& S_{1,l}^{i,4}$。如果$\Delta S_{2,l}^{i,2} = 1$, $\Delta S_{3,l}^{i,2} = \Delta S_{4,l}^{i,2} = 0$，令$\Delta Y_l^{i,0} = 1$可以降低$\Delta S_{2,l}^{i,3}$的重量，这个非0差分产生了“好的影响”。当$\Delta S_{4,l}^{i,3} = 0$或者$\Delta S_{1,l}^{i,4} = 0$时，$\Delta Y_l^{i,0} = 1$使得上面两个与门变成了活跃的，但当$\Delta S_{4,l}^{i,3} = \Delta S_{1,l}^{i,4} = 1$时，这两个与门必然是活跃的，则$\Delta Y_l^{i,0} = 1$对这两个与门的活跃性不会产生实质性影响。综上当$\Delta S_{2,l}^{i,2} = \Delta S_{4,l}^{i,3} = \Delta S_{1,l}^{i,4} = 1$, $\Delta S_{3,l}^{i,2} = \Delta S_{4,l}^{i,2} = 0$时，$\Delta Y_l^{i,0} = 1$将会产生“好的影响”，由此给出了如下差分推导规则：

(1) 当与门属于A类情况时，$\Delta Y_l^{i,0}$可以唯一确定；

(2) 当与门属于B类情况时，如果满足条件：$\Delta S_{2,l}^{i,2} = \Delta S_{4,l}^{i,3} = \Delta S_{1,l}^{i,4} = 1$且$\Delta S_{3,l}^{i,2} = \Delta S_{4,l}^{i,2} = 0$，则令$\Delta Y_l^{i,0} = 1$，否则令$\Delta Y_l^{i,0} = 0$。

对于第$i$步状态更新函数中其他轮的与门同样如此，由此得到了状态更新函数完整的差分推导规则。本文需要确定初始状态的差分便可以进行差分推导，MORUS的初始化阶段的初始状态中$S_2^{0,0}$, $S_3^{0,0}$, $S_4^{0,0}$是已知常数，差分固定为0，$S_1^{0,0}$是密钥，在实际攻击中无法控制但可以进行多次加密，差分同样固定为0。$S_0^{0,0}$只与${\text{IV}}$有关，由于${\text{IV}}$是已知的，可以选择${{\Delta {\rm{IV}}}}$的值，根据经验${{\Delta {\rm{IV}}}}$的重量为1时，更有可能得到好的差分链，此时$\Delta S_0^{0,0}$的值有128种可能。来看第1步状态更新函数第4轮的与门$S_{0,l}^{0,3}\& S_{4,l}^{0,3}$，其中$\Delta S_{0,l}^{0,3} = \Delta S_{0,l}^{0,0}$，$S_{4,l}^{0,3}$的值是已知的，当$\Delta S_{0,l}^{0,3} = \Delta S_{0,l}^{0,0} = 1$时，如果$S_{4,l}^{0,3} = 1$, $\Delta (S_{0,l}^{0,3}\& S_{4,l}^{0,3}) = 1$，产生了一个非0差分，如果$S_{4,l}^{0,3} = 0$, $\Delta (S_{0,l}^{0,3}\& S_{4,l}^{0,3}) = 0$，这表明了$\Delta S_0^{0,0}$中1的位置对差分传递是有影响的，据此给出了$\Delta S_0^{0,0}$的候选集合。令$\Delta (l')(l' \in \{ 0,1, \cdots , 127\} )$表示一个128 bit块，其第$l'$ bit为1，其余bit为0。

对于MORUS-640，$\Delta S_0^{0,0}$的候选集合为

对于MORUS-1280，$\Delta S_0^{0,0}$的候选集合为

加入移位操作，上面的分析仍然可行，在实际攻击中，把所有操作都考虑在内。表3给出了利用该差分推导规则得到的较高的差分转移概率。

本文将表4与现有最好的结果进行对比，文献[16]中给出了MORUS-640状态更新步数为5,6,7时的差分转移概率分别为${2^{ - 228}}$, ${2^{ - 301}}$, ${2^{ - 455}}$，当步数为5,7时，找到了概率更高的差分链，步数为6时，差分转移概率相同。另外，文献[16]中并未给出MORUS-1280的结果。

表 4  MORUS初始化阶段差分转移概率

状态更新步数	1	2	3	4	5	6	7
MORUS-640	${2^{ - 1}}$	${2^{ - 8}}$	${2^{ - 29}}$	${2^{ - 82}}$	${2^{ - 180}}$	${2^{ - 301}}$	${2^{ - 453}}$
MORUS-1280	${2^{ - 1}}$	${2^{ - 8}}$	${2^{ - 29}}$	${2^{ - 86}}$	${2^{ - 201}}$	${2^{ - 399}}$	${2^{ - 681}}$

下载: 导出CSV 

| 显示表格

4.   MORUS的MILP差分分析

第3节的差分推导规则只能保证找到的差分链中活跃与门数量尽可能少，采用的是局部最优的思想。本节给出了MORUS的MILP差分自动搜索方法，以第3节的结果为基础，利用分而治之思想，搜索全局最优的差分链。MORUS的状态更新函数包括5轮子函数，本节将状态更新以轮为单位，例如，进行16轮状态更新就是进行3.2步状态更新函数。

根据MORUS算法初始化阶段的初始状态装填，可以得到初始状态差分$\Delta {S^{0,0}} = (\Delta S_0^{0,0},\Delta S_1^{0,0},\Delta S_2^{0,0}, \Delta S_3^{0,0},\Delta S_4^{0,0})$如表5所示。

表 5  MORUS初始化阶段的初始状态差分$\Delta {S^{0,0}}$

	MORUS-640	MORUS-1280
$\Delta S_0^{0,0}$	${{\Delta {\rm{IV}}} }$	${{\Delta {\rm{IV}}} }||{0^{128} }$
$\Delta S_1^{0,0}$	${0^{128}}$	${0^{256}}$
$\Delta S_2^{0,0}$	${0^{128}}$	${0^{256}}$
$\Delta S_3^{0,0}$	${0^{128}}$	${0^{256}}$
$\Delta S_4^{0,0}$	${0^{128}}$	${0^{256}}$

下载: 导出CSV 

| 显示表格

对于初始化阶段的前4轮状态更新，在已知差分${{\Delta {\rm{IV}}}}$的情况下，手动推导可以得到以概率1成立的差分链，所以本文的MILP模型从初始化阶段的第5轮状态更新开始刻画，这样做可以大大减少模型中变量与不等式的数量，从而提高MILP模型的求解速度。表6给出了已知$\Delta {\rm{IV }}$第5轮状态更新的输入差分$\Delta {S^{0,4}} = (\Delta S_0^{0,4},\Delta S_1^{0,4},\Delta S_2^{0,4},\Delta S_3^{0,4},\Delta S_4^{0,4})$，这是容易推导得到的。

表 6  MORUS初始化阶段第5轮状态更新的输入差分$\Delta {S^{0,4}}$

	MORUS-640	MORUS-1280
$\Delta S_0^{0,4}$	${\text{Rot\_128\_32(} }\Delta {\rm{IV}},{b_0}) < << {w_2}$	${\text{Rot\_256\_64(} }\Delta {\rm{IV}}||{0^{128} },{b_0}) < << {w_2}$
$\Delta S_1^{0,4}$	${0^{128}}$	${0^{256}}$
$\Delta S_2^{0,4}$	${\text{Rot\_128\_32(} }\Delta {\rm{IV}},{b_0} + {b_2})$	${\text{Rot\_256\_64(} }\Delta {\rm{IV}}||{0^{128} },{b_0} + {b_2})$
$\Delta S_3^{0,4}$	${\text{Rot\_128\_32}}(\Delta S_0^{0,4}\& (S_4^{0,0} < < < {w_1}),{b_3})$	${\text{Rot\_256\_64}}(\Delta S_0^{0,4}\& (S_4^{0,0} < < < {w_1}),{b_3})$
$\Delta S_4^{0,4}$	${0^{128}}$	${0^{256}}$

下载: 导出CSV 

| 显示表格

4.1   MILP差分模型构建

MORUS初始化阶段的主要运算包括移位、模2加、与门。首先给出这些运算的MILP刻画，其中移位只涉及变量下标的变换，不需要额外的不等式进行刻画。

对于模2加$a \oplus b = c$，可以用下面等式刻画其差分特性，这里需要引入一个新变量${\text{dummy}}$

对于与门$a{\text{\& }}b = c$，可以用不等式(15)刻画其差分特性

将每一轮中的模2加和与门看作一个整体$a \oplus (b\& c) \oplus d = e$去刻画其差分特性

这样刻画将增加不等式的个数，但也大大减少了变量的个数。表7给出了对于$R$轮状态更新这两种刻画方式的比较。

表 7  MORUS子轮函数两种刻画方式的比较

刻画方式	(2)+(3)	(4)
变量个数	$3Rn$	$Rn$
不等式个数	$2Rn$	$4Rn$

下载: 导出CSV 

| 显示表格

对于一个$R$轮状态更新，原本的刻画方式(2)+(3)需要引入新的变量来刻画与门的输出差，还要引入辅助变量${\text{dummy}}$来刻画模2加，其变量个数是新的刻画方式(4)的3倍，从实验结果来看，刻画方式(4)加快了MILP模型的求解速度。

第$r$轮输出差分$\Delta S_0^{\left\lfloor {r/5} \right\rfloor ,r\bmod 5},\Delta S_1^{\left\lfloor {r/5} \right\rfloor ,r\bmod 5}, \Delta S_2^{\left\lfloor {r/5} \right\rfloor ,r\bmod 5},\Delta S_3^{\left\lfloor {r/5} \right\rfloor ,r\bmod 5},\Delta S_4^{\left\lfloor {r/5} \right\rfloor ,r\bmod 5}$，为了进一步减少MILP模型中变量的个数，只对$\Delta S_{(r{{ - }}1)\bmod 5}^{\left\lfloor {r/5} \right\rfloor ,r\bmod 5}$进行刻画，其余4个bit块没有发生改变或者只进行了简单移位，不需要进行重复的刻画。

MILP模型中除了设置变量与约束条件，还需要定义目标函数，本文的目标是求解${r_1}$～${r_2}$轮状态更新中活跃与门数量的最小值，目标函数设为($|$表示逻辑或，$n=128或256$)

本节建立了以下3种MILP模型：

(1) ${\mathcal{M}_R}$：目标函数为求解MORUS初始化阶段$R$轮状态更新中活跃与门数量的最小值。

(2) $\mathcal{M}[{r_1},{r_2}][{W_{\Delta {\text{IV}}}} \ge x]$：目标函数为求解MORUS初始化阶段第${r_1}$～${r_2}$轮状态更新中活跃与门数量的最小值，限制${{\Delta {\rm{IV}}}}$的重量大于等于$x$，也用${W_{{{\Delta {\rm{IV}}}}}} = x$表示${{\Delta {\rm{IV}}}}$的重量等于$x$。

(3) $\mathcal{M}[{r_1},{r_2}][{D_r} = \Delta S]$：目标函数为求解MORUS初始化阶段第${r_1}$～${r_2}$轮状态更新中活跃与门数量的最小值，限制第$r$轮的输入差分为$\Delta S$。

为了叙述方便，将模型(2), (3)统一记为$\mathcal{M}[{r_1},{r_2}] [{\text{Con}}]$，${\text{Con}}$表示限制条件。用${\text{Sol}}({\text{ }})$表示模型的解，本文的目的是求解${\text{Sol}}({\mathcal{M}_R})$，其他模型作为辅助模型，下文将根据分而治之思想求解${\text{Sol}}({\mathcal{M}_R})$。

4.2   分而治之策略

在利用MILP搜索差分链时，当轮数增加，搜索最优差分链的难度将呈指数级增加，要解决的首要问题是如何提高求解MILP模型的速度。2019年，Zhou等人^[14]针对SPN结构，提出了分而治之策略以提高MILP模型的搜索能力，受他们的启发，为了使MOURS的MILP差分模型尽可能搜索更多轮，基于已有的差分链搜索经验我们提出了适用于MORUS的分而治之策略。分而治之策略的思想是将求解一个MILP模型的问题划分为求解多个MILP子模型的问题，其中大部分子模型的求解可以利用一些方法提前终止，这就大大减少了搜索时间。对于SPN结构的分组密码，输入输出差分是可以任意取值的，与SPN结构的分组密码不同的是，MORUS给定了状态的初始值，所以其初始状态差分也受到限制，这使得在搜索差分链时要“沿着”状态更新的方向。

根据第4节开始部分的分析，由于MORUS初始化阶段1～4轮的差分传递是以概率1成立的，不需要考虑1～4轮的活跃与门，所以求解${\text{Sol}}({\mathcal{M}_R})$实际上只需求解${\text{Sol}}(\mathcal{M}[5,R][{W_{{{\Delta {\rm{IV}}}}}} \ge 1])$。MORUS初始化阶段的初始状态中，只有${\text{IV}}$是可以控制的，$\Delta {\text{IV}} = 0$则整个初始状态差分为0，考虑这种情况是没有意义的，将${{\Delta {\rm{IV}}}}$根据重量分为3种情况考虑：$|\Delta {\text{IV}}| = 1$, $|\Delta {\text{IV}}| = 2$, $|\Delta {\text{IV}}| \ge 3$，对应地模型$\mathcal{M}[5,R] [{W_{\Delta {\text{IV}}}} \ge 1]$被划分为3个子模型$\mathcal{M}[5,R][{W_{\Delta {\text{IV}}}} = 1]$, $\mathcal{M}[5,R][{W_{\Delta {\text{IV}}}} = 2]$, $\mathcal{M}[5,R][{W_{\Delta {\text{IV}}}} \ge 3]$，则有

由表6，当${{\Delta {\rm{IV}}}}$确定时，其对应的第5轮输入差分记为

${{\Delta {\rm{IV}}}}$的重量为$x$时，取值有$C_{128}^x$种，对应的$\Delta {S^{0,4}}(\Delta {\text{IV}})$的取值有$C_{128}^x$种，记$\Delta {S^{0,4}}(\Delta {\text{IV}})$这$C_{128}^x$种取值组成的集合为${\varOmega _x}$，则有定理1。

定理1　对于MORUS初始化阶段的MILP差分模型${\mathcal{M}_R}$，有

证明　根据上文的讨论$\mathcal{M}[5,R][{W_{{{\Delta {\rm{IV}}}}}} = x]$可以进一步划分为多个子模型$\mathcal{M}[5,R][{D_5} = \Delta S](\Delta S \in {\varOmega _x})$，所以${\text{Sol}}(\mathcal{M}[5,R][{W_{{{\Delta {\rm{IV}}}}}} = x]) = \mathop {\min }\limits_{\Delta S \in {\varOmega _x}} {\text{Sol}}(\mathcal{M}[5,R] [{D_5} = \Delta S])$，则有

证毕

定义1　对于${\text{MORUS - }}5n{\text{ }}(n = 128,256)$的两个差分状态$\Delta S = (\Delta {S_0},\Delta {S_1},\Delta {S_2},\Delta {S_3},\Delta {S_4})$, $\Delta {S^ * } = (\Delta S_0^ * ,\Delta S_1^ * ,\Delta S_2^ * ,\Delta S_3^ * ,\Delta S_4^ * )$，若存在$b \in \left\{ 0,1, \cdots , {n}/{4} - 1\right\}$, $w \in \left\{ 0,{n}/{4}, {{2n}}/{4}, {{3n}}/{4}\right\}$，使得对于所有$i \in \{ 0,1,2,3,4\}$, $\Delta {S_i} = {\text{Rot\_}}x{\text{\_}}y{\text{(}}\Delta S_i^ * ,b) < < < w{\text{ }}$成立，则称这两个差分状态是关于$(b,w)$循环等价的，或简称循环等价。

定理2　若差分状态$\Delta S$, $\Delta {S^ * }$是循环等价的，那么${\text{Sol}}(\mathcal{M}[{r_1},{r_2}][{D_r} = \Delta S]) = {\text{Sol}}(\mathcal{M}[{r_1},{r_2}][{D_r} = \Delta {S^ * }])$。

证明　假设$\Delta S$,$\Delta {S^ * }$是关于$(b,w)$循环等价的，对于MILP差分模型$\mathcal{M}[{r_1},{r_2}][{D_r} = \Delta S]$，假设${\text{Sol}}(\mathcal{M} [{r_1},{r_2}][{D_r} = \Delta S]) = {\text{NA}}$，则对应一条差分链$L$，其第$r$轮输入差分是$\Delta S$，第${r_1}$～${r_2}$轮活跃与门数量为${\text{NA}}$，显然存在一条差分链${L^ * }$，其每一轮的差分状态与$L$中对应轮的差分状态均是关于$(b,w)$循环等价的，特别地，其第$r$轮输入差分是$\Delta {S^ * }$，${L^ * }$的第${r_1}$至${r_2}$轮活跃与门数量为${\text{NA}}$，所以有

同理有

所以${\text{Sol}}(\mathcal{M}[{r_1},{r_2}][{D_r} = \Delta S]) = {\text{Sol}}(\mathcal{M}[{r_1},{r_2}][{D_r} = \Delta {S^ * }])$。

证毕

根据定义1，容易知道循环等价关系具有自反性、对称性、传递性，所以根据循环等价的定义将${\varOmega _1}$, ${\varOmega _2}$中的差分状态进行分类，表8给出了MORUS-640与MORUS-1280的分类个数。

表 8  ${\varOmega _1}$, ${\varOmega _2}$的分类个数

	MORUS-640	MORUS-1280
${\varOmega _1}$	2	2
${\varOmega _2}$	257	382

下载: 导出CSV 

| 显示表格

在${\varOmega _1}$, ${\varOmega _2}$的每一个分类中，任取一个元素作为代表元，这些代表元组成集合$\varOmega _1^ *$, $\varOmega _2^ *$，得到推论1。

推论1　对于MORUS初始化阶段的MILP差分模型${\mathcal{M}_R}$，有

证明　结合定理1、定理2以及$\varOmega _1^ *$,$\varOmega _2^ *$的定义，推论1是显然的。证毕

根据推论1，把求解MORUS初始化阶段$R$轮状态更新中最优差分链的问题转化为求解多个MILP子模型的问题，这些子模型按照${{\Delta {\rm{IV}}}}$的重量分为3类：$\{ \mathcal{M}[5,R][{D_5} = \Delta S]|\Delta S \in \varOmega _1^ * \}$, $\{ \mathcal{M}[5,R] [{D_5} = \Delta S]|\Delta S \in \varOmega _2^ * \}$, $\mathcal{M}[5,R][{W_{{{\Delta {\rm{IV}}}}}} \ge 3]$，分别对应了$|\Delta {\text{IV}}| = 1$, $|\Delta {\text{IV}}| = 2$, $|\Delta {\text{IV}}| \ge 3$，根据经验，${{\Delta {\rm{IV}}}}$的重量越小，越容易搜索到好的差分链，所以按如下顺序求解MILP子模型：$\{ \mathcal{M}[5,R] [{D_5} = \Delta S] |\Delta S \in \varOmega _1^ * \}$, $\{ \mathcal{M}[5,R][{D_5} = \Delta S]|\Delta S \in \varOmega _2^ * \}$, $\mathcal{M}[5,R] [{W_{{{\Delta {\rm{IV}}}}}} \ge 3]$，为了方便描述，本文定义了一个有序集合

集合长度为$|{\text{Set}}|$，用$\mathcal{M}\left( i \right)$表示集合${\text{Set}}$的第$i$个元素($i \in \{ 1,2, \cdots ,|{\text{Set}}|\}$)，由表7，对于MORUS-640，$|{\text{Set}}| = 2 + 257 + 1 = 260$，对于MORUS-1280，$|{\text{Set}}| = 2 + 382 + 1 = 385$。

另外，为了更快计算这些MILP子模型，本文定义了两个指标：

(1)最小活跃与门数量上界。对于MORUS初始化阶段$R$轮状态更新，${\text{U}}{{\text{B}}_R}$表示当前最优差分链的活跃与门数量。本文利用第3节的差分推导规则得到当前最优的差分链，并以其活跃与门数量作为初始的${\text{U}}{{\text{B}}_R}$，在整个搜索过程中，如果找到了一条更好的差分链${\text{U}}{{\text{B}}_R}$将被更新。

(2)MILP差分模型$\mathcal{M}[{r_1},{r_2}][{\text{Con}}]$活跃与门数量下界。对于MILP差分模型$\mathcal{M}[{r_1},{r_2}][{\text{Con}}]$, ${\text{LB}}[{r_1},{r_2}][{\text{Con}}]$表示该模型最优解(即活跃与门数量的最小值)的下界。

定理3　对于MILP差分模型$\mathcal{M}[{r_1},{r_2}][{\text{Con}}]$, $\mathop {\max }\limits_{{r_1} \le r' < {r_2}} ({\text{LB}}[{r_1},r'][{\text{Con}}] + {\text{LB}}[r' + 1,{r_2}][{\text{Con}}])$是该模型中活跃与门数量的下界。

证明　假设模型$\mathcal{M}[{r_1},{r_2}][{\text{Con}}]$的最优差分链为$L$，对于任意$r'$：${r_1} \le r' < {r_2}$，差分链$L$可以分成两部分：一条${r_1}$～$r'$轮差分链${L_1}$，一条$r' + 1$～${r_2}$轮差分链${L_2}$。${\text{NA}}(L)$, ${\text{NA}}({L_1})$, ${\text{NA}}({L_2})$分别表示$L$, ${L_1}$, ${L_2}$的活跃与门数量，显然${\text{NA}}(L) = {\text{NA}}({L_1}) + {\text{NA}}({L_2})$，又有${\text{NA}}({L_1}) \ge {\text{LB}}[{r_1},r'][{\text{Con}}]$, ${\text{NA}}({L_2}) \ge {\text{LB}}[r' + 1,{r_2}][{\text{Con}}]$，则

所以，${\text{LB}}[{r_1},r'][{\text{Con}}] + {\text{LB}}[r' + 1,{r_2}][{\text{Con}}]$是MILP差分模型$\mathcal{M}[{r_1},{r_2}][{\text{Con}}]$中差分链活跃与门数量的下界，$\mathop {\max }\limits_{{r_1} \le r' < {r_2}} ({\text{LB}}[{r_1},r'][{\text{Con}}] + {\text{LB}}[r' + 1,{r_2}][{\text{Con}}])$也是$\mathcal{M}[{r_1},{r_2}][{\text{Con}}]$中差分链活跃与门数量的下界。

证毕

定理3给出了计算$\mathcal{M}[{r_1},{r_2}][{\text{Con}}]$活跃与门数量下界的一种方法，对于轮数较少的模型，可以通过直接求解MILP模型得到其最小活跃与门数量从而获得最“紧致”的下界，也就是令${\text{LB}}[{r_1},{r_2}] [{\text{Con}}] = {\text{Sol}}(\mathcal{M}[{r_1},{r_2}][{\text{Con}}])$；本文将利用Gurobi求解器求解所有模型，如果轮数较多可以通过将Gurobi中的参数MIPFocus设置为3，从而快速求得$\mathcal{M}[{r_1},{r_2}][{\text{Con}}]$的活跃与门数量下界。本文之所以将MORUS初始化阶段以轮为单位，就是为了充分利用定理3给出模型更加紧致的活跃与门数量下界。算法1给出了${\text{Sol}}({\mathcal{M}_R})$完整的求解过程。

算法1　基于MILP分而治之策略搜索MORUS初始化阶段差分链
输入：$R$
输出：${\text{Sol}}({\mathcal{M}_R})$
步骤1　根据第3节的差分推导规则，计算${\text{U}}{{\text{B}}_R}$的初始值，令 　　　　 $i = 0$；
步骤2　令$i = i + 1$；
步骤3　计算${\text{LB}}(\mathcal{M}\left( i \right))$，如果${\text{LB} }(\mathcal{M}\left( i \right)) \ge {\text{U} }{ {\text{B} }_R}$，返回步骤2， 　　　　 否则，执行步骤4；
步骤4　求解${\text{Sol}}(\mathcal{M}\left( i \right))$，如果${\text{Sol}}(\mathcal{M}\left( i \right)) < {\text{U}}{{\text{B}}_R}$，令 　　　　 ${\text{U}}{{\text{B}}_R} = {\text{Sol}}(\mathcal{M}\left( i \right))$；
步骤5　如果$i = |{\text{Set}}|$，输出${\text{U}}{{\text{B}}_R}$，否则，返回步骤2。

下载: 导出CSV 

| 显示表格

利用算法1，分别令$R$取5,10,15,20,25,30得到了MORUS-640与MORUS-1280初始化阶段状态更新步数为1～6的最优结果，如表9所示。表9与第3节中差分推导规则得到的结果相比：对于MORUS-640，状态更新步数为5,6时，得到了更好的差分链；对于MORUS-1280，状态更新步数为6时，得到了更好的差分链。可以看出，当状态更新步数较小时，第3节中的差分推导规则可以得到最优的差分链，但当步数增加时，基于分而治之策略的MILP模型可以找到更好的差分链。

表 9  MILP模型中MORUS初始化阶段的最优差分转移概率

	状态更新步数
	1	2	3	4	5	6
MORUS-640	${2^{ - 1}}$	${2^{ - 8}}$	${2^{ - 29}}$	${2^{ - 82}}$	${2^{ - 179}}$	${2^{ - 279}}$
MORUS-1280	${2^{ - 1}}$	${2^{ - 8}}$	${2^{ - 29}}$	${2^{ - 86}}$	${2^{{\text{ - 201}}}}$	${2^{ - 379}}$

下载: 导出CSV 

| 显示表格

4.3   简化版MORUS的差分-区分攻击

本节给出初始化阶段为$g$步的简化版MORUS的差分-区分攻击，图2给出了简化版MORUS的示意图，这里令相关数据部分为空，图2只展示了初始化阶段与第1个密钥流块的生成。简化版MORUS经过$g$步初始化阶段的状态更新，其输出产生了第1个密钥流块$Z$

图 2  简化版MORUS示意图

下载: 全尺寸图片 幻灯片

前面所讨论的是初始状态$(S_0^{0,0},S_1^{0,0},S_2^{0,0}, S_3^{0,0}, S_4^{0,0})$到第$g$步输出状态$(S_0^{g,0},S_1^{g,0},S_2^{g,0},S_3^{g,0},S_4^{g,0})$的差分链，为了对密钥流块$Z$进行差分-区分攻击，本文需要找到一条初始状态$(S_0^{0,0},S_1^{0,0},S_2^{0,0},S_3^{0,0},S_4^{0,0})$到第1个密钥流块$Z$概率较大的差分链，区别在于：这里不需要考虑第$g$步第5轮的与门，而需要考虑式(25)中的与门，这是因为$S_4^{g,0}$不参与$Z$的计算。本文建立了相应的MILP模型去寻找这样的差分链，求解过程仍利用了4.2节给出的分而治之策略，表10给出了搜索结果以及与目前最好结果的对比。

表 10  简化版MORUS差分-区分攻击的差分转移概率

状态更新步数	MORUS-640			MORUS-1280
	文献[16]	本文		文献[16]	本文
3	${2^{ - 38}}$	${2^{ - 32}}$		–	${2^{ - 32}}$
4	${2^{ - 101}}$	${2^{ - 89}}$		–	${2^{ - 91}}$
5	–	${2^{ - 184}}$		–	${2^{ - 207}}$
6	–	${2^{ - 284}}$		–	${2^{ - 380}}$

下载: 导出CSV 

| 显示表格

文献[16]只给出了初始化阶段为3步、4步的简化版MORUS-640的差分-区分攻击，并未给出MORUS-1280的攻击结果。对于MORUS-640，其密钥流块$Z$的长度为128，本文给出了初始化阶段为3步、4步的简化版MORUS-640的差分-区分攻击，本文搜索到的差分链优于文献[16]的结果；对于MORUS-1280，其密钥流块$Z$的长度为256，本文给出了初始化阶段为4步、5步的简化版MORUS-1280的差分-区分攻击，攻击结果见表11。

表 11  简化版MORUS的差分-区分攻击

算法	状态更新步数	差分转移概率	数据量	区分优势
MORUS-640	3	${2^{ - 32}}$	${2^{35}}$	0.999665
	4	${2^{ - 89}}$	${2^{92}}$	0.999665
MORUS-1280	4	${2^{ - 91}}$	${2^{94}}$	0.999665
	5	${2^{ - 207}}$	${2^{210}}$	0.999665

下载: 导出CSV 

| 显示表格

5.   结束语

本文主要对MORUS初始化阶段的差分性质进行研究，首先给出一个改进的差分推导规则，能够快速找到一条较好的差分链。在此基础上，利用MILP自动搜索技术寻找最优差分链，为了提高MILP模型求解速度而采用了分而治之策略，得到了初始化阶段1～6步的最优差分链，最后利用得到的差分链对简化版的MORUS进行差分-区分攻击。本文的结果较之前的工作有较大提升，下一步将考虑把分而治之方法运用到MORUS的线性分析中，尝试给出MORUS更优的线性分析结果。