惠普忆阻电路的线性叠加分析

丁芝侠; 黄莎莉; 李赛; 杨乐

doi:10.11999/JEIT220733

惠普忆阻电路的线性叠加分析

doi: 10.11999/JEIT220733

武汉工程大学电气信息学院武汉 430205

基金项目: 国家自然科学基金(62176189, 62106181)

详细信息

作者简介:
丁芝侠：女，博士，副教授，研究方向为分数阶神经网络动力学分析及应用、忆阻神经形态系统、深度学习与类脑智能

黄莎莉：女，硕士生，研究方向为忆阻电路设计、忆阻神经形态系统

李赛：男，博士，讲师，研究方向为机器学习理论、控制与优化理论、动态系统的故障诊断

杨乐：男，博士，讲师，研究方向为忆阻神经形态系统、深度学习与类脑智能、忆阻电路设计

通讯作者:
杨乐　leyangmail@163.com

中图分类号: TN601
计量
- 文章访问数: 428
- HTML全文浏览量: 270
- PDF下载量: 93
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-06
- 修回日期: 2022-09-02
- 录用日期: 2022-09-06
- 网络出版日期: 2022-09-09
- 刊出日期: 2023-07-10

Linear Superposition Analysis of HP Memristor Circuits

School of Electrical and Information Engineering, Wuhan Institute of Technology, Wuhan 430205, China

Funds: The National Natural Science Foundation of China (62176189, 62106181)

摘要

摘要: 基于惠普(HP)忆阻器的元件特性，该文分析了惠普忆阻器的数学关系式，惠普忆阻元件的内部状态变量与忆阻阻值之间存在增量线性关系，在外加电压下惠普忆阻器阻值的变化可叠加，得出了惠普忆阻电路具有线性叠加性的结论。通过PSpice电路仿真验证上述结论的有效性和正确性，为叠加定理在含惠普忆阻器及线性元件的线性电路中的使用提供了理论分析支撑。
- 惠普忆阻电路 /
- 惠普忆阻器 /
- 增量线性 /
- 叠加定理 /
- PSpice仿真
Abstract: Based on the component characteristics of Hewlett Packard(HP) memristor, the mathematical relationship formula of HP memristor is analyzed. There is an incremental linear relationship between the internal state variables of HP memristor components and the value of memristor. The change of the value of HP memristor can be superimposed under applied voltage, and the conclusion is drawn that HP memristor circuit has linear superposition. The validity and correctness of the above conclusions are verified by PSpice circuit simulation, which provides theoretical analysis support for the use of the superposition theorem in linear circuits containing HP memristors and linear components.
- Hewlett Packard(HP) memristor circuit /
- HP memristor /
- Incremental linear /
- Superposition theorem /
- PSpice simulation

HTML全文

图 1 HP忆阻器的物理结构图

下载: 全尺寸图片幻灯片

图 2 反向求和运算电路的仿真电路图

下载: 全尺寸图片幻灯片

图 3 输入为直流电压源时运放的输出

下载: 全尺寸图片幻灯片

图 4 外加直流电压下$ {R_{\text{M}}} $上的变化

下载: 全尺寸图片幻灯片

图 5 输入为方波信号源时运放的输出

下载: 全尺寸图片幻灯片

图 6 外加方波电压下$ {R_{\text{M}}} $上的变化

下载: 全尺寸图片幻灯片

图 7 输入为正弦波信号源时运放的输出

下载: 全尺寸图片幻灯片

图 8 外加正弦波电压下$ {R_{\text{M}}} $上的变化

下载: 全尺寸图片幻灯片

表 1 直流电压下忆阻电路的输出电压值(V)

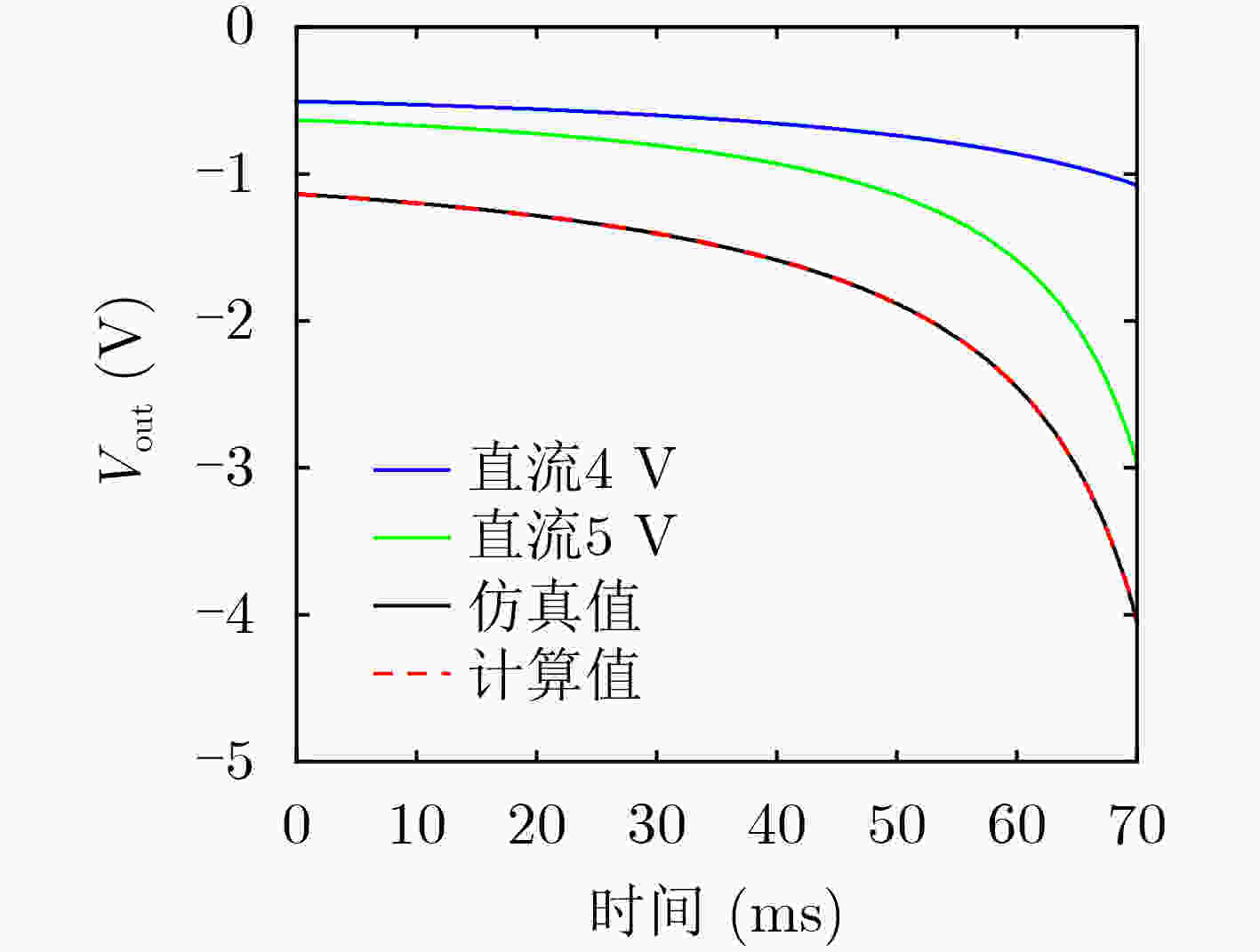
时间(ms)	V_out1	V_out2	V_测量	V_计算
0	–0.505	–0.632	–1.136	–1.137
5	–0.516	–0.650	–1.166	–1.166
10	–0.529	–0.671	–1.199	–1.200
15	–0.543	–0.696	–1.239	–1.239
20	–0.560	–0.726	–1.285	–1.286
25	–0.579	–0.762	–1.340	–1.341
30	–0.601	–0.806	–1.406	–1.407
35	–0.627	–0.860	–1.486	–1.487
40	–0.657	–0.930	–1.587	–1.587
45	–0.694	–1.021	–1.715	–1.715
50	–0.739	–1.145	–1.884	–1.884

下载: 导出CSV

表 2 方波电压下忆阻电路的输出电压值(V)

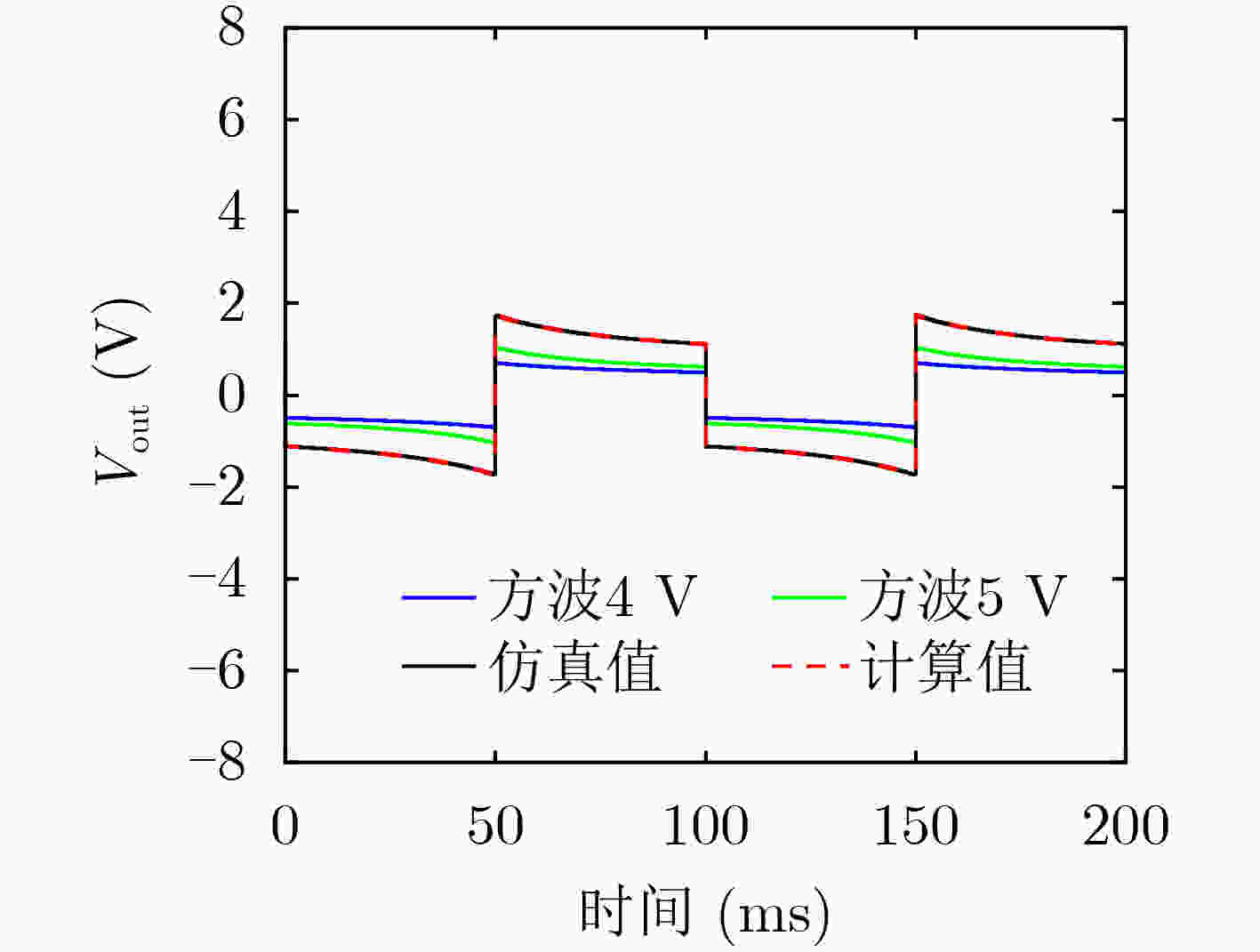
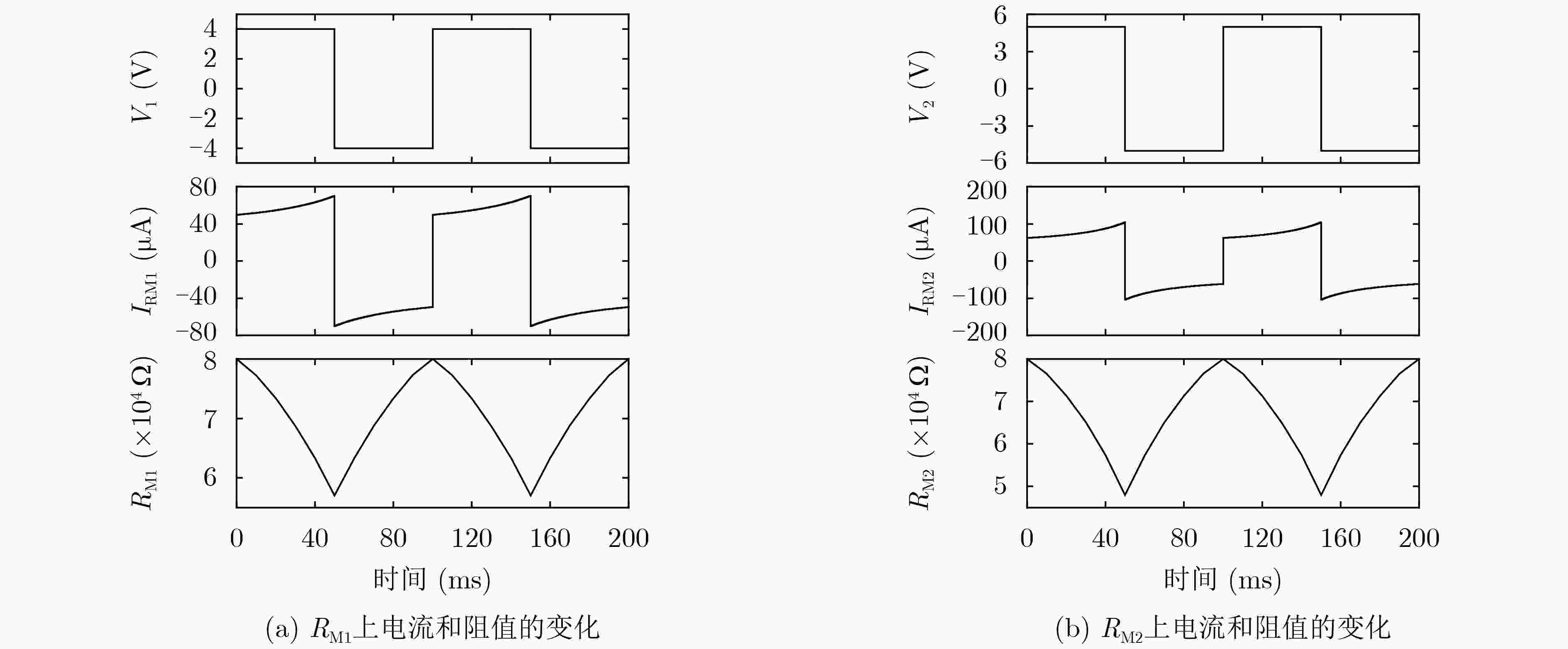
时间(ms)	V_out1	V_out2	V_测量	V_计算
0	0.495	0.618	1.114	1.113
10	–0.518	–0.654	–1.172	–1.172
20	–0.546	–0.701	–1.247	–1.247
30	–0.583	–0.769	–1.351	–1.352
40	–0.632	–0.873	–1.504	–1.505
50	–0.702	–1.042	–1.744	–1.744
60	0.631	0.871	1.503	1.502
70	0.581	0.768	1.350	1.349
80	0.545	0.700	1.246	1.245
90	0.517	0.653	1.170	1.170
100	0.496	0.618	1.115	1.114

下载: 导出CSV

表 3 正弦波电压下忆阻电路的输出电压值(V)

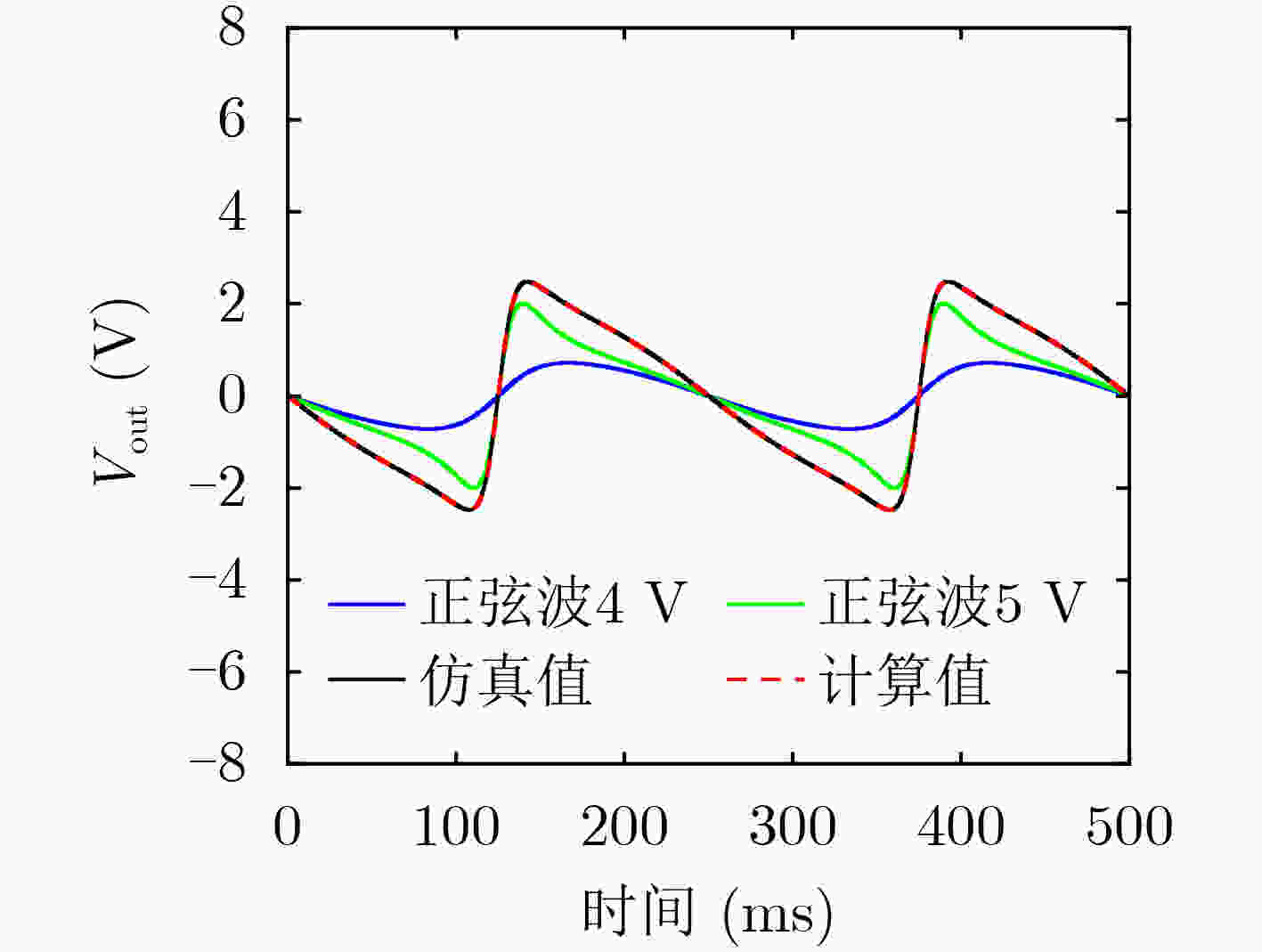
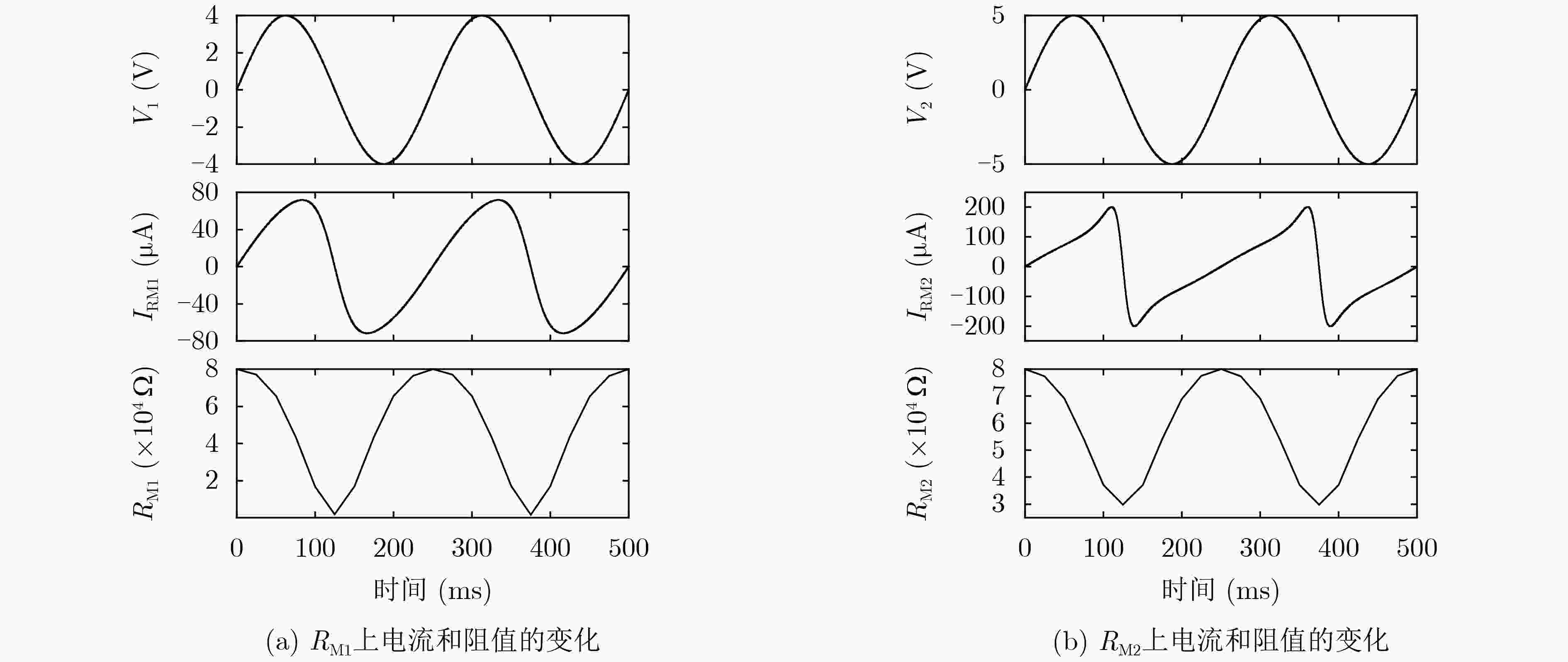
时间(ms)	V_out1	V_out2	V_测量	V_计算
0	0	0	0	0
25	–0.305	–0.384	–0.688	–0.689
50	–0.552	–0.728	–1.280	–1.280
75	–0.703	–1.090	–1.793	–1.793
100	–0.632	–1.735	–2.366	–2.367
125	0	0	0	0
150	0.631	1.732	2.364	2.363
175	0.702	1.088	1.790	1.790
200	0.551	0.726	1.277	1.277
225	0.303	0.382	0.685	0.685
250	0	0	0	0

下载: 导出CSV

参考文献(24)

[1]	CHUA L O. Memristor-the missing circuit element[J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507–519. doi: 10.1109/TCT.1971.1083337
[2]	STRUKOV D B, SNIDER G S, STEWART D R, et al. The missing memristor found[J]. Nature, 2008, 453(7191): 80–83. doi: 10.1038/nature06932
[3]	TOUR J M and HE Tao. Electronics: The fourth element[J]. Nature, 2008, 453(7191): 42–43. doi: 10.1038/453042a
[4]	王小平, 沈轶, 吴计生, 等. 忆阻及其应用研究综述[J]. 自动化学报, 2013, 39(8): 1170–1184. doi: 10.3724/SP.J.1004.2013.01170 WANG Xiaoping, SHEN Yi, WU Jisheng, et al. Review on memristor and its applications[J]. Acta Automatica Sinica, 2013, 39(8): 1170–1184. doi: 10.3724/SP.J.1004.2013.01170
[5]	YANG J J, PICKETT M D, LI Xuema, et al. Memristive switching mechanism for metal/oxide/metal nanodevices[J]. Nature Nanotechnology, 2008, 3(7): 429–433. doi: 10.1038/nnano.2008.160
[6]	SHIMA H and TAMAI Y. Oxide nanolayer improving RRAM operational performance[J]. Microelectronics Journal, 2009, 40(3): 628–632. doi: 10.1016/j.mejo.2008.06.096
[7]	LI Can, GRAVES C E, SHENG Xia, et al. Analog content-addressable memories with memristors[J]. Nature Communications, 2020, 11(1): 1638. doi: 10.1038/s41467-020-15254-4
[8]	孙晶茹, 李梦圆, 康可欣, 等. 基于异构忆阻器的1T2M多值存储交叉阵列设计[J]. 电子与信息学报, 2021, 43(6): 1533–1540. doi: 10.11999/JEIT201108 SUN Jingru, LI Mengyuan, KANG Kexin, et al. Design of heterogeneous memristor based 1T2M multi-value memory crossbar array[J]. Journal of Electronics &Information Technology, 2021, 43(6): 1533–1540. doi: 10.11999/JEIT201108
[9]	ALI K A, RIZK M, BAGHDADI A, et al. Crossbar memory architecture performing memristor overwrite logic[C]. 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 2019: 723–726.
[10]	LUO Li, DONG Zhekang, DUAN Shukai, et al. Memristor-based stateful logic gates for multi-functional logic circuit[J]. IET Circuits, Devices & Systems, 2020, 14(6): 811–818. doi: 10.1049/iet-cds.2019.0422
[11]	闵富红, 王珠林, 王恩荣, 等. 新型忆阻器混沌电路及其在图像加密中的应用[J]. 电子与信息学报, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178 MIN Fuhong, WANG Zhulin, WANG Enrong, et al. New Memristor chaotic circuit and its application to image encryption[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178
[12]	马铭磷, 刘颖, 李志军. 忆阻开关混沌电路及其吸引子共存现象研究[J]. 电子与信息学报, 2021, 43(12): 3758–3765. doi: 10.11999/JEIT200689 MA Minglin, LIU Ying, and LI Zhijun. Study on coexistence of Multipe attractors in memristor-based switching chaotic circuits[J]. Journal of Electronics &Information Technology, 2021, 43(12): 3758–3765. doi: 10.11999/JEIT200689
[13]	瞿少成, 陈尧, 罗静, 等. 一种单输入控制器下的忆阻混沌同步电路设计与实现[J]. 电子与信息学报, 2022, 44(1): 400–407. doi: 10.11999/JEIT200947 QU Shaocheng, CHEN Yao, LUO Jing, et al. Design and implementation of Memristor-based chaotic synchronization under a single input controller[J]. Journal of Electronics &Information Technology, 2022, 44(1): 400–407. doi: 10.11999/JEIT200947
[14]	王春华, 蔺海荣, 孙晶如, 等. 基于忆阻器的混沌、存储器及神经网络电路研究进展[J]. 电子与信息学报, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821 WANG Chunhua, LIN Hairong, SUN Jingru, et al. Research progress on chaos, memory and neural network circuits based on memristor[J]. Journal of Electronics &Information Technology, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821
[15]	ZHOU Chao, WANG Chunhua, SUN Yichuang, et al. Weighted sum synchronization of memristive coupled neural networks[J]. Neurocomputing, 2020, 403: 211–233. doi: 10.1016/j.neucom.2020.04.087
[16]	LIN Hairong, WANG Chunhua, HONG Qinghui, et al. A multi-stable memristor and its application in a neural network[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2020, 67(12): 3472–3476. doi: 10.1109/TCSII.2020.3000492
[17]	YANG Le, ZENG Zhigang, HUANG Yi, et al. Memristor-based circuit implementations of recognition network and recall network with forgetting stages[J]. IEEE Transactions on Cognitive and Developmental Systems, 2018, 10(4): 1133–1142. doi: 10.1109/TCDS.2018.2859303
[18]	YANG Le, ZENG Zhigang, and WEN Shiping. A full-function Pavlov associative memory implementation with memristance changing circuit[J]. Neurocomputing, 2018, 272: 513–519. doi: 10.1016/j.neucom.2017.07.020
[19]	HONG Qinghui, YAN Renao, WANG Chunhua, et al. Memristive circuit implementation of biological nonassociative learning mechanism and its applications[J]. IEEE Transactions on Biomedical Circuits and Systems, 2020, 14(5): 1036–1050. doi: 10.1109/TBCAS.2020.3018777
[20]	ZHANG Yutong and ZENG Zhigang. A Multi-functional memristive Pavlov associative memory circuit based on neural mechanisms[J]. IEEE Transactions on Biomedical Circuits and Systems, 2021, 15(5): 978–993. doi: 10.1109/TBCAS.2021.3108354
[21]	ADHIKARI S P, YANG Changju, KIM H, et al. Memristor bridge synapse-based neural network and its learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(9): 1426–1435. doi: 10.1109/TNNLS.2012.2204770
[22]	WILLIAMS R S. How we found the missing memristor[J]. IEEE Spectrum, 2008, 45(12): 28–35. doi: 10.1109/MSPEC.2008.4687366
[23]	龙际磊. 线性电路的分析方法[J]. 电脑知识与技术, 2014, 10(23): 5543–5545. doi: 10.14004/j.cnki.ckt.2014.0214 LONG Jilei. Analysis of linear circuits[J]. Computer Knowledge and Technology, 2014, 10(23): 5543–5545. doi: 10.14004/j.cnki.ckt.2014.0214
[24]	彭军. “纯电阻元件”与“线性元件”概念讨论[J]. 物理通报, 2017(8): 101–103. doi: 10.3969/j.issn.0509-4038.2017.08.033 PENG Jun. Discussion on the concepts of pure resistance elements and linear elements[J]. Physics Bulletin, 2017(8): 101–103. doi: 10.3969/j.issn.0509-4038.2017.08.033