基于算术平均融合的分布式多伯努利扩展目标跟踪

吴孙勇; 郑翔飞; 李天成; 胡青霜; 吕晓燕

doi:10.11999/JEIT220688

基于算术平均融合的分布式多伯努利扩展目标跟踪

doi: 10.11999/JEIT220688

吴孙勇^{1, 2},
郑翔飞^1, ,,
李天成³,
胡青霜¹,
吕晓燕¹

1.
桂林电子科技大学数学与计算科学学院桂林 541004
2.
广西密码学与信息安全重点实验室桂林 541004
3.
西北工业大学自动化学院西安 710071

基金项目: 国家自然科学基金(62263007, 62061010,62161007, 62071389)，中央引导地方科技发展资金项目(2022YZX2001)，广西科技厅项目(AA19182007)，广西密码学与信息安全重点实验室研究课题(GCIS202132)，桂林电子科技大学数学与计算科学学院研究生创新项目(2022YJSCX02)，桂林电子科技大学研究生教育创新计划(2022YCXS145)

详细信息

作者简介:
吴孙勇：男，教授，博士生导师，研究方向为阵列信号处理、信息融合、弱目标检测和跟踪等

郑翔飞：男，硕士生，研究方向为扩展目标跟踪、多传感信息融合、随机有限集

李天成：男，教授，博士生导师，研究方向为多传感信息融合、多目标跟踪、雷达组网等

胡青霜：女，硕士生，研究方向为扩展目标跟踪、随机有限集

吕晓燕：女，硕士生，研究方向为扩展目标跟踪、随机有限集

通讯作者:
郑翔飞　zxf_double@163.com

中图分类号: TN911.73; TP391
计量
- 文章访问数: 619
- HTML全文浏览量: 285
- PDF下载量: 140
- 被引次数: 0
出版历程
- 收稿日期: 2022-05-27
- 修回日期: 2022-09-03
- 网络出版日期: 2022-09-08
- 刊出日期: 2023-06-10

Distributed Multi-Bernoulli Extended Targets Tracking Based on Arithmetic Average Fusion

1.
Mathematics and Computer Science College of Guilin University of Electronic Technology, Guilin 541004, China
2.
Guangxi Key Laboratory of Cryptography and Information Security, Guilin 541004, China
3.
School of Automation, Northwestern Polytechnical University, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (62263007,62061010, 62161007, 62071389), The Central Government Guided Local Science and Technology Development Fund Project (2022YZX2001), Guangxi Science and Technology Department Project (AA19182007), Guangxi Key Laboratory of Cryptography and Information Security (GCIS202132), The Graduate Innovation Program of School of Mathematics and Computing Science, GUET (2022YJSCX02), The Innovation Project of GUET Graduate Education (2022YCXS145)

摘要

摘要: 在分布式传感网络中，由于同一扩展目标的方位角以及轴长等状态参数在不同传感器下估计结果不一致，因此多扩展目标估计关联困难，从而为后续密度信息融合带来了巨大挑战。相比于点目标后验密度信息，扩展目标后验密度同时包含了质心状态和外形信息。该文结合质心欧氏距离和外形矩阵非欧氏尺寸-形状度量提出了椭圆距离(ED)，该椭圆距离同时考虑了扩展目标质心状态与外形信息，更好地实现了不同传感器下同一扩展目标后验密度关联。此外该文在算术平均(AA)融合规则下推导了融合空间密度的近似伽马高斯逆威沙特(GGIW)分布，实现了不同传感器下同一扩展目标后验信息AA融合。仿真实验表明，该文所提算法在分布式传感网络中能有效地进行多扩展目标跟踪。
- 分布式网络 /
- 扩展目标 /
- 椭圆距离 /
- 算术平均 /
- 伽马高斯逆威沙特分布
Abstract: In distributed sensor networks, the inconsistent estimation results of state parameters such as azimuth and axis lengths of the same extended target under different sensors lead to the difficulty of extended target estimation association, which gives rise to challenges to the subsequent density information fusion. Compared with the point target posterior density information, the extended target posterior density contains both centroid state and shape information. Moreover, the Ellipse Distance (ED) is proposed based on the Euclidean distance of centroid and non-Euclidean size-shape metric of shape matrix. The ellipse distance considers both the centroid state and shape information of the extended target, and better realizes the posterior density correlation of the same extended target under different sensors. In addition, in this paper, the approximate Gamma Gaussian Inverse Wishart (GGIW) distribution of fusion space density is derived under the Arithmetic Average (AA) fusion rule, and the AA fusion of posterior information of the same extended target under different sensors is realized. Simulation results show that the proposed algorithm can effectively track multiple extended targets in distributed sensor networks.
- Distributed network /
- Extended target /
- Ellipse Distance (ED) /
- Arithmetic Average(AA) /
- Gamma Gaussian Inverse Wishart (GGIW) distribution

HTML全文

图 1 跟踪结果

下载: 全尺寸图片幻灯片

图 2 目标个数

下载: 全尺寸图片幻灯片

图 3 OSPA误差图

下载: 全尺寸图片幻灯片

图 4 GOSPA误差图

下载: 全尺寸图片幻灯片

图 5 平均OSPA误差图

下载: 全尺寸图片幻灯片

图 6 平均GOSPA误差图

下载: 全尺寸图片幻灯片

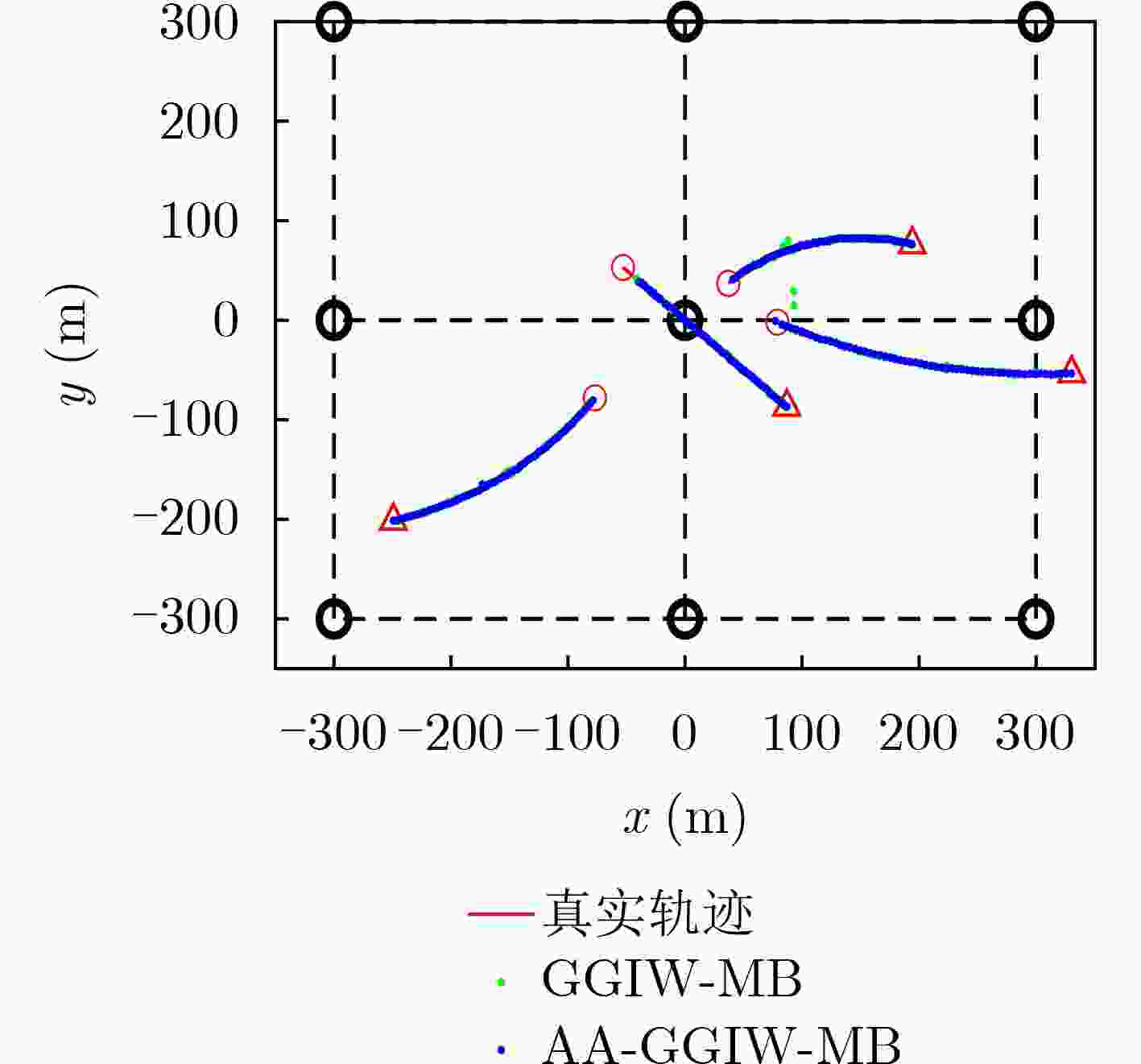
表 1 场景内目标状态及存活时间

目标	目标质心状态	出现时刻(s)	消失时刻(s)
目标1	[75; 4; 0; –2; $\pi $ /360]	1	59
目标2	[–75; –2; –75; –3;–$\pi $/270]	10	69
目标3	[35; 2; 35; 2; –$\pi $/180]	20	69
目标4	[–55; 2; 55; –2; 0]	30	100

下载: 导出CSV

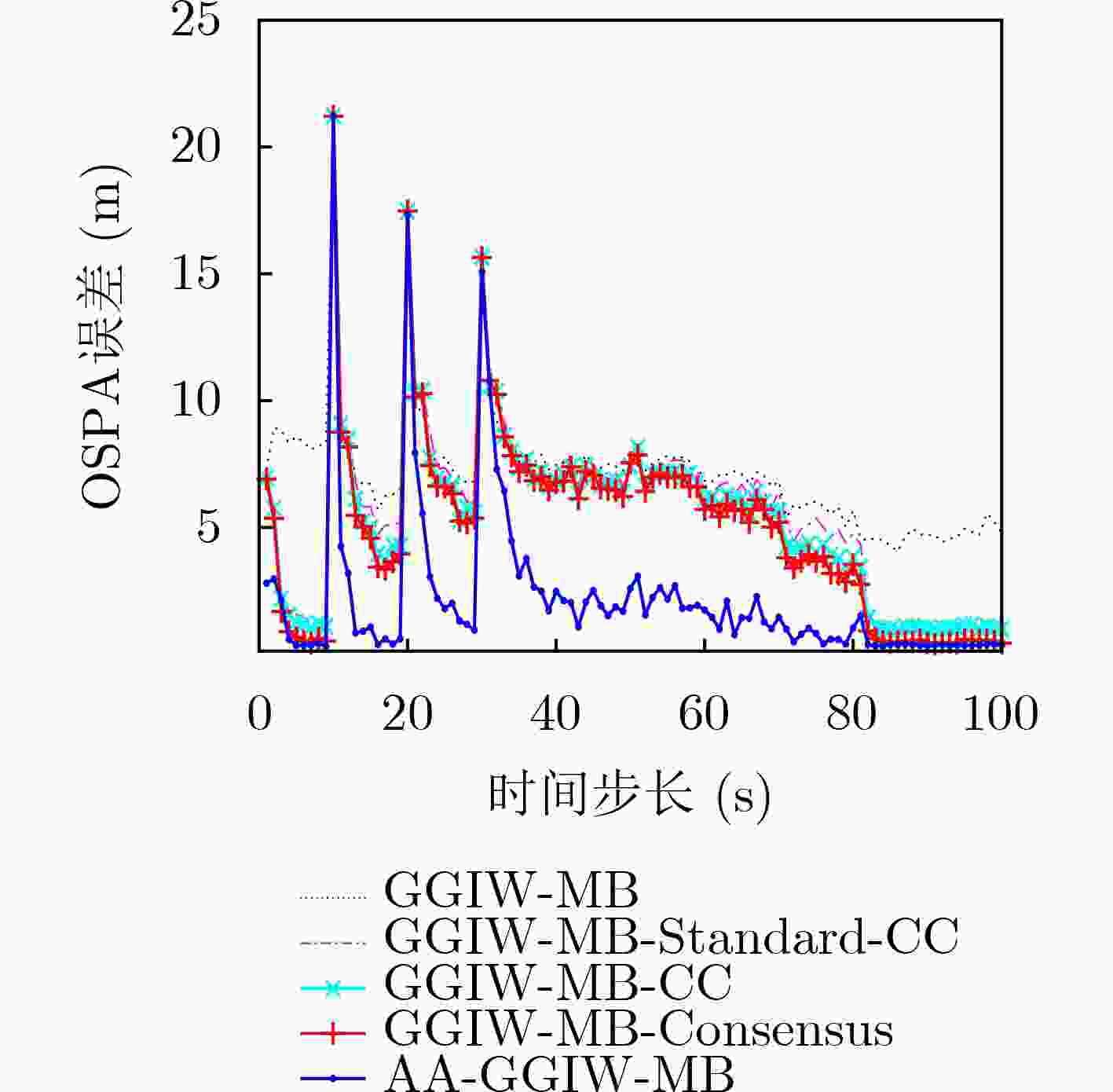
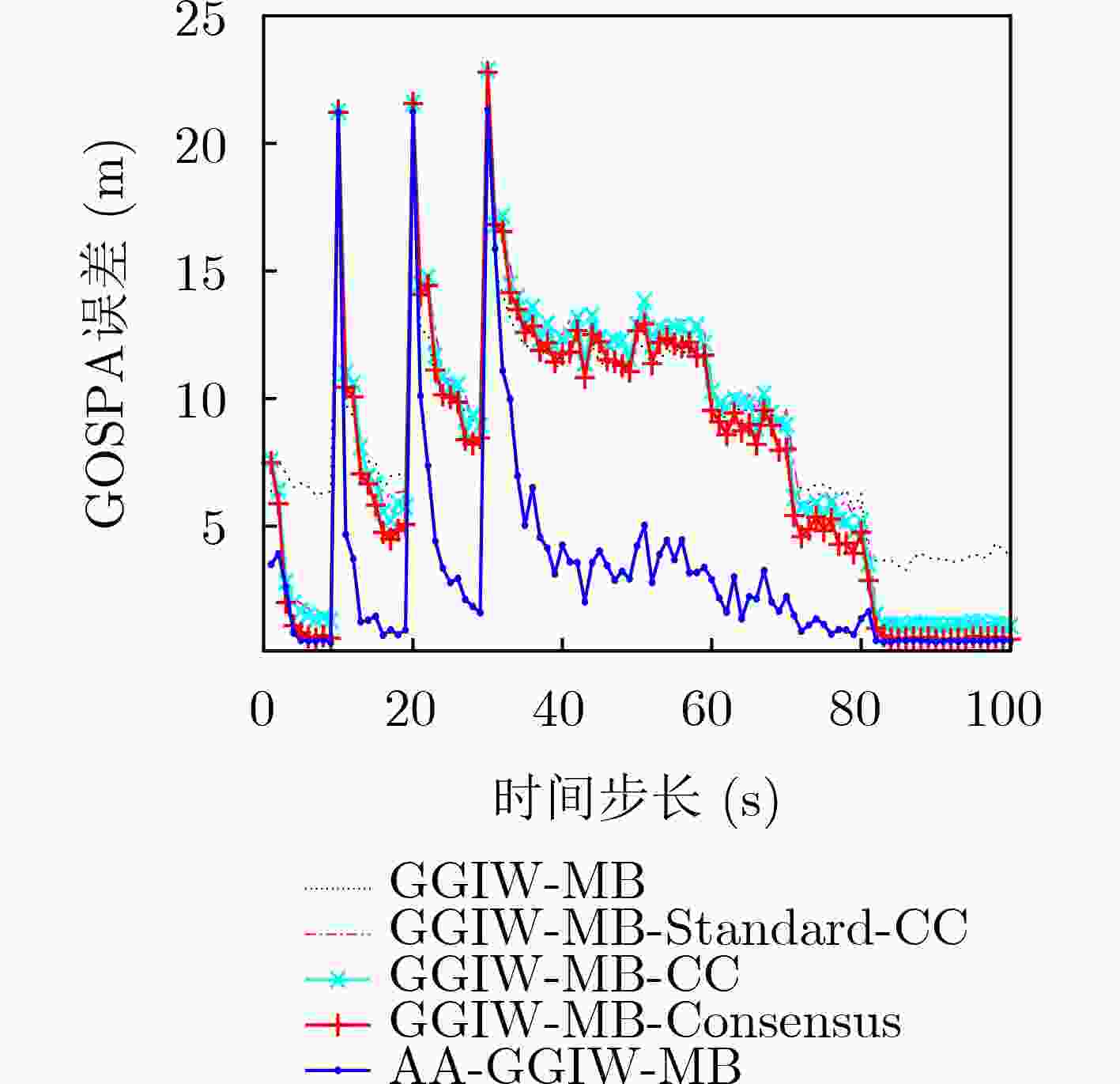
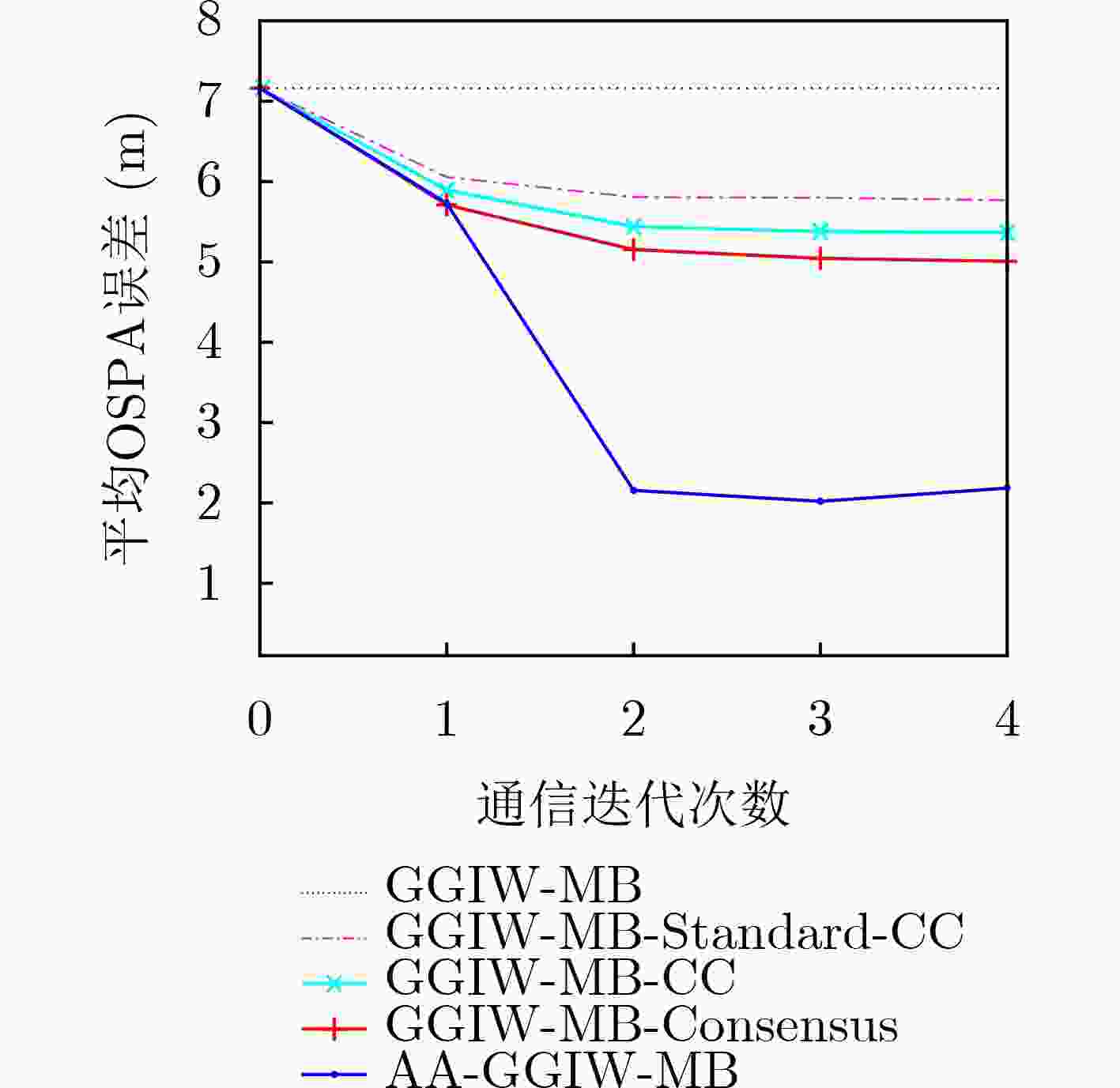
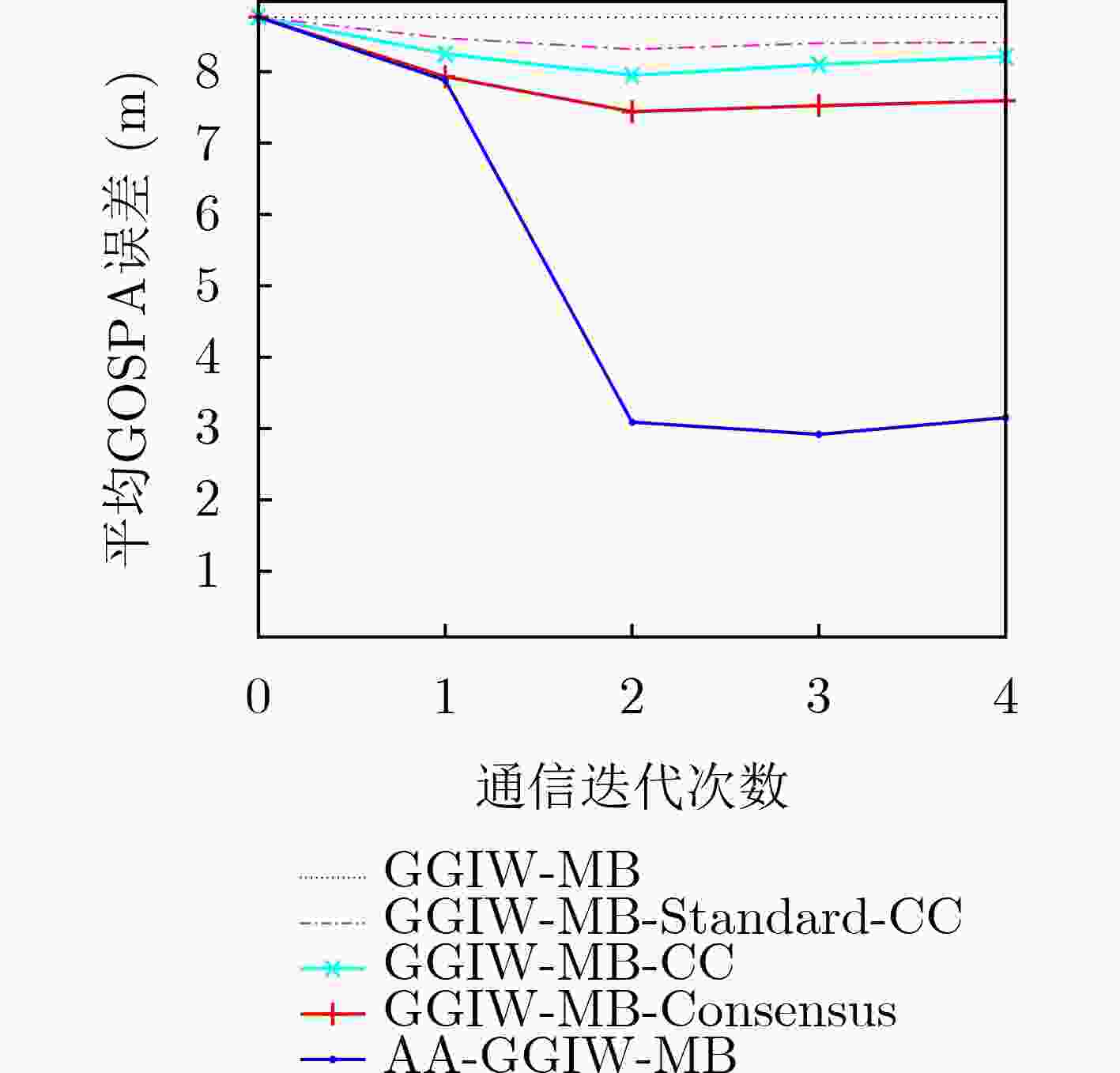
表 2 不同场景设置参数$\left( {{\rm{Pd}},{\lambda _\kappa } } \right)$的GOSPA误差和OSPA误差(m)

	(0.7,30)		(0.7,60)		(0.9,30)		(0.9,60)
	GOSPA	OSPA	GOSPA	OSPA	GOSPA	OSPA	GOSPA	OSPA
GGIW-MB	1764.0	1440.4	1843.8	1510.4	904.7	729.6	933.1	757.3
AA-GGIW-MB	1492.0	1134.5	1463.6	1107.6	372.4	242.7	382.1	249.4

下载: 导出CSV

参考文献(24)

[1]	DA Kai, LI Tiancheng, ZHU Yongfeng, et al. Recent advances in multisensor multitarget tracking using random finite set[J]. Frontiers of Information Technology & Electronic Engineering, 2021, 22(1): 5–24. doi: 10.1631/FITEE.2000266
[2]	GAO Lin, BATTISTELLI G, and CHISCI L. Multiobject fusion with minimum information loss[J]. IEEE Signal Processing Letters, 2020, 27: 201–205. doi: 10.1109/LSP.2019.2963817
[3]	杨标, 朱圣棋, 余昆, 等. 贪婪的量测划分机制下的多传感器多机动目标跟踪算法[J]. 电子与信息学报, 2021, 43(7): 1962–1969. doi: 10.11999/JEIT200498 YANG Biao, ZHU Shengqi, YU Kun, et al. Multi-sensor multiple maneuvering targets tracking algorithm under greedy measurement partitioning mechanism[J]. Journal of Electronics &Information Technology, 2021, 43(7): 1962–1969. doi: 10.11999/JEIT200498
[4]	LI Tiancheng and HLAWATSCH F. A distributed particle-PHD filter using arithmetic-average fusion of Gaussian mixture parameters[J]. Information Fusion, 2021, 73: 111–124. doi: 10.1016/j.inffus.2021.02.020
[5]	BATTISTELLI G, CHISCI L, FANTACCI C, et al. Consensus CPHD filter for distributed multitarget tracking[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 508–520. doi: 10.1109/JSTSP.2013.2250911
[6]	MAHLER R P S. Optimal/robust distributed data fusion: A unified approach[C]. SPIE 4052, Signal Processing, Sensor Fusion, and Target Recognition IX, Orlando, USA, 2000: 128–138.
[7]	DA Kai, LI Tiancheng, ZHU Yongfeng, et al. Kullback-Leibler Averaging for Multitarget Density Fusion[M]. Cham: Springer, 2020: 253–261.
[8]	LI Tiancheng, FAN Hongqi, GARCÍA J, et al. Second-order statistics analysis and comparison between arithmetic and geometric average fusion: Application to multi-sensor target tracking[J]. Information Fusion, 2019, 51: 233–243. doi: 10.1016/j.inffus.2019.02.009
[9]	LI Tiancheng, CORCHADO J M, and PRIETO J. Convergence of distributed flooding and its application for distributed Bayesian filtering[J]. IEEE Transactions on Signal and Information Processing over Networks, 2017, 3(3): 580–591. doi: 10.1109/TSIPN.2016.2631944
[10]	LI Tiancheng, CORCHADO J M, and SUN Shudong. Partial consensus and conservative fusion of Gaussian Mixtures for distributed PHD fusion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(5): 2150–2163. doi: 10.1109/TAES.2018.2882960
[11]	THORMANN K and BAUM M. Fusion of elliptical extended object estimates parameterized with orientation and axes lengths[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(4): 2369–2382. doi: 10.1109/TAES.2021.3057651
[12]	LI Guchong, LI Gang, and HE You. Distributed GGIW-CPHD-Based extended target tracking over a sensor network[J]. IEEE Signal Processing Letters, 2022, 29: 842–846. doi: 10.1109/LSP.2022.3158589
[13]	裴佳. 基于随机超曲面的多扩展目标跟踪算法研究[D]. [硕士论文], 西安电子科技大学, 2017. PEI Jia. Research on algorithms of multiple extended targets tracking based on random hypersurface model[D]. [Master dissertation], Xidian University, 2017.
[14]	LUNDQUIST C, GRANSTRÖM K, and ORGUNER U. An extended target CPHD filter and a gamma Gaussian inverse Wishart implementation[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 472–483. doi: 10.1109/JSTSP.2013.2245632
[15]	连峰, 马冬冬, 元向辉, 等. 扩展目标CBMeMBer滤波器及其高斯混合实现[J]. 控制与决策, 2015, 30(4): 611–616. doi: 10.13195/j.kzyjc.2014.0286 LIAN Feng, MA Dongdong, YUAN Xianghui, et al. CBMeMBer filter for extended targets and its Gaussian mixture implementations[J]. Control and Decision, 2015, 30(4): 611–616. doi: 10.13195/j.kzyjc.2014.0286
[16]	LI Tiancheng, WANG Xiaoxu, LIANG Yan, et al. On arithmetic average fusion and its application for distributed Multi-Bernoulli multitarget tracking[J]. IEEE Transactions on Signal Processing, 2020, 68: 2883–2896. doi: 10.1109/TSP.2020.2985643
[17]	YANG Shishan, BAUM M, and GRANSTRÖM K. Metrics for performance evaluation of elliptic extended object tracking methods[C]. 2016 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems. Baden-Baden, Germany, 2016: 523–528.
[18]	DRYDEN I L, KOLOYDENKO A, and ZHOU K D. Non-Euclidean statistics for covariance matrices, with applications to diffusion tensor imaging[J]. The Annals of Applied Statistics, 2009, 3(3): 1102–1123. doi: 10.1214/09-AOAS249
[19]	LI Tiancheng, LIU Zhunga, and PAN Quan. Distributed Bernoulli filtering for target detection and tracking based on arithmetic average fusion[J]. IEEE Signal Processing Letters, 2019, 26(12): 1812–1816. doi: 10.1109/LSP.2019.2950588
[20]	GIVENS C R and SHORTT R M. A class of Wasserstein metrics for probability distributions[J]. The Michigan Mathematical Journal, 1984, 31(2): 231–240. doi: 10.1307/mmj/1029003026
[21]	GRANSTRÖM K and ORGUNER U. On the reduction of Gaussian Inverse Wishart mixtures[C]. 2012 15th International Conference on Information Fusion, Singapore, 2012: 2162–2169.
[22]	GRANSTRÖM K and ORGUNER U. Estimation and maintenance of measurement rates for multiple extended target tracking[C]. 2012 15th International Conference on Information Fusion, Singapore, 2012: 2170–2176.
[23]	RAHMATHULLAH A S, GARCÍA-FERNÁNDEZ Á F, and SVENSSON L. Generalized optimal sub-pattern assignment metric[C]. 2017 20th International Conference on Information Fusion, Xi'an, China, 2017: 1–8.
[24]	VO B T, VO B N, HOSEINNEZHAD R, et al. Robust Multi-Bernoulli filtering[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 399–409. doi: 10.1109/JSTSP.2013.2252325