Network Defense Decision-making Method Based on Improved Evolutionary Game Model
-
摘要: 针对网络防御决策的误差干扰和实时响应问题,该文提出一种改进演化博弈模型(IEGM)和网络防御决策方法。首先,借鉴经典伺服系统模型,用微分假设量化表示防御方对攻击策略的短期预测效应,加快模型收敛速度,提升防御决策效率。其次,分析攻防博弈中的误差产生机理,量化定义网络防御中的观测误差,提出改进复制动力学方程,加强模型对信息偏差的容忍度。在此基础上,建立改进演化博弈模型,证明了模型能够收敛至纳什均衡解的微小
$ \varepsilon $ -邻域,给出了相应的稳定性分析,并设计了一种网络防御决策方法。理论分析和仿真结果表明,所提模型能够克服观测误差影响,给出偏差数量级在0.01%的最优防御纯策略,且在强干扰环境下,防御决策的响应速度相较于其他3种经典决策模型最高可以提升64.06%。改进模型和防御决策方法能够有效提升防御决策的响应时效性和对观测误差的适应性。Abstract: For the problem that the existing network defense decision-making method is challenging by error interference and real-time response, a novel network defense decision-making method based on an Improved Evolutionary Game Model (IEGM) is proposed. Firstly, using the classical servo system model for reference, the short-term prediction effect of the defense side on the attack strategy is quantified by differential hypothesis to accelerate the convergence of the model and improve the efficiency of defense decisions. Secondly, the mechanism of error generation in attack-defense game is analyzed, then the observational error in network defense is defined quantitatively, and the improved replication dynamics equation is proposed to strengthen the tolerance of the model to information deviation. On this basis, an improved evolutionary game model is established, and the corresponding stability analysis and mathematical proof are given to prove that the model can converge to the$ \varepsilon $ -neighborhood of the Nash equilibrium solution. Theoretical analysis and simulation results show that the proposed model can overcome the influence of observation error, and the optimal pure defense strategy with deviation order of 0.01% is given. Besides, under the jamming environment, the response speed of defense decision-making can be improved by 64.06% compared with the other three decision models. The improved model and decision-making method can effectively improve the response timeliness of defense decisions and the adaptability to observation error. -
表 1 原子攻击策略
序号 原子攻击动作名称 所利用漏洞编号 感染概率$ \lambda $ 攻击成本$ {A_{{\text{cost}}}} $ $ {a_1} $ Web资源管理
漏洞攻击CNNVD-202104-989 0.78 0.20 $ {a_2} $ Oracle数据库
输入验证攻击CNNVD-202107-1424 0.89 0.15 $ {a_3} $ Word插件路径
遍历攻击CNNVD-202109-701 0.93 0.10 $ {a_4} $ Microsoft Edge
跨站脚本攻击CNNVD-202109-106 0.73 0.25 表 2 原子防御策略
序号 原子防御动作名称 防御动作描述 操作代价$ {D_{{\text{cost}}}} $ 防御效果$ \phi $ b1 设置黑洞路由 利用防火墙修改路由表到不可达IP 0.30 0.59 b2 丢弃可疑数据包 利用IDS进行包过滤 0.10 0.25 b3 限制用户活动 限制可疑用户的权限及活动 0.50 0.83 b4 格式化硬盘 格式化硬盘去除所有恶意代码 0.80 0.99 算法1 最优防御纯策略选取算法 输入:国家信息安全漏洞库CNNVD
输出:最优防御纯策略集合优防御纯策略集合$S_{\rm{D}} $(Best)
BEGIN
(1) /* 初始化改进演化博弈模型 */
Initialize IEGM=$(N,S,P,{P}'_{\text{A} } ,U,\epsilon ,\dot{P})$;
{
(a) Construct $ N = ({N_{\text{A}}},{N_{\text{D}}}) $;
/* 构建网络攻防异质群体博弈参与者空间 */
(b) Construct $ S = ({S_{\text{A}}},{S_{\text{D}}}) $;
/* 根据表1、表2构建混合策略空间 */
(c) Construct $ P = ({P_{\text{A}}},{P_{\text{D}}}) $;
/* 创建待赋值的实际博弈信念空间 */
(d) Construct ${P'_{\text{A} } } = ({P'_{ {\text{A1} } } } ,{P'_{ {\text{A2} } } } , \cdots ,{P'_{ {\text{A} }j} } )$;
/* 根据历史数据构建攻击方经验博弈信念空间 */
(e) Construct $ U = ({U_{\text{A}}},{U_{\text{D}}}) $;
/* 创建待赋值的博弈收益空间 */
(f) Assign $ e(t) \in [ - 1,1] $;
/* 为观测误差赋值随机数 */
(g) Construct $\dot{P}=(\dot{ {P}_{\text{A} } },\dot{ {P}_{\text{D} } })$;
/* 创建待赋值的短期预测集合 */
}
(2) /* 计算攻防博弈收益 */
For $ (n = 1;n \le i;n + + ) $
For $ (m = 1;m \le j;m + + ) $
{
Calculate $\left\{\begin{array}{l}{U}_{{\rm{D}}}=\varphi \text{ }·\text{ }{V}_{\text{r} }-{D}_{\text{cost} }\\ {U}_{{\rm{A}}}=\lambda \text{ }·\text{ }{V}_{\text{r} }-{A}_{\text{cost} }{D}_{\mathrm{cos}t}\end{array} \right.$;${\bf{Calculate} }\left\{\begin{array}{l}{\overline{U} }_{\text{D} }={\displaystyle {\sum }_{n=1}^{i}{P}_{\text{D}n}\cdot {U}_{\text{D}n}\text{ } },\;\text{ }1\le n\le i\\ {\overline{U} }_{\text{A} }={\displaystyle {\sum }_{m=1}^{j}{P}_{\text{A}m}\cdot {U}_{\text{A}m}\text{ } },\text{ }1\le m\le j\end{array} \right.$;
}
(3) /* 构建改进复制动态方程 */
For $ (n = 1;n \le i;n + + ) $
For $ (m = 1;m \le j;m + + ) $
{
Construct ${ \dot{P}_{\text{D}i} }=\beta ({P}_{\text{A}j}(t)+e(t)+ {\dot {P}_{\text{A}j}(t)})-{\displaystyle {\sum }_{n=1}^{i}{P}_{\text{D}n}\text{(}t\text{) }·\text{ }{U}_{\text{D}n}(t)\text{ } }$;
}
(4) /* 模型求解 */
Define function
/* 定义微分方程求解函数 */
function =
@(t)[${ \dot{P}_{\text{D}i} }=\beta ({P}_{\text{A}j}(t)+ {\dot {P}_{\text{A}j}(t)+e}(t))-{\displaystyle {\sum }_{n=1}^{i}{P}_{\text{D}n}\text{(}t\text{) }·\text{ }{U}_{\text{D}n}(t)\text{ } }$];
Assign t;
/* 为计算时长T赋值 */
For $ (n = 1;n \le i;n + + ) $
{
ode45(function, T, $ P $);
/* 利用MATLAB ode45函数对方程进行求解 */
When $ {P_{{\text{D}}i}} = 1 $
Return $ {S_{\text{D}}}({\text{Best}}) $;
/* 当防御方博弈信念为1时输出最优防御纯策略 */
Else
Return 0;
}
END表 3 实验3参数设置
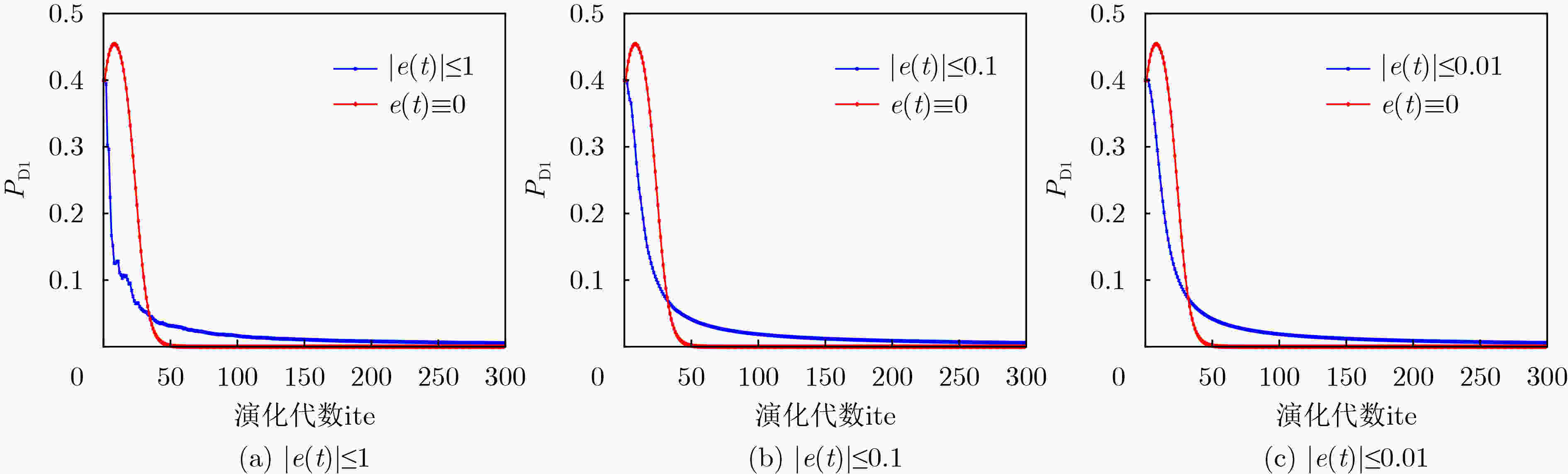
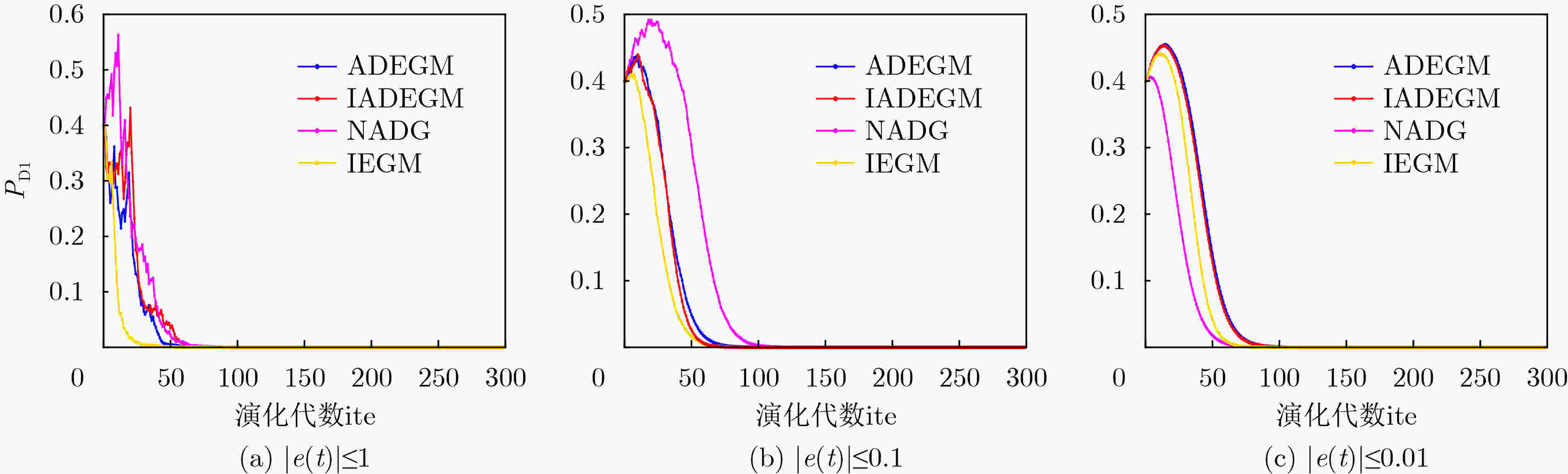
模型 $ {u_1} $ $ {u_2} $ $ {P_{{\text{A1}}}} $ $ {P_{{\text{D1}}}} $ 其他参数 IEGM 0.22 0.26 0.6 0.4 $ \left| {e(t)} \right| = (0,\delta ] $ ADEGM 0.22 0.26 0.6 0.4 – NADG 0.22 0.26 0.6 0.4 – IADEGM 0.22 0.26 0.6 0.4 $ {\lambda _{21}} = 1 $ 表 4 实验3中模型收敛至最优解所需演化代数
模型 $ \left| {e(t)} \right| \le 1 $ $ \left| {e(t)} \right| \le 0.1 $ $ \left| {e(t)} \right| \le 0.01 $ IEGM 67 94 91 ADEGM 82 104 115 NADG 99 133 94 IADEGM 110 98 117 -
[1] ALPCAN T and BAŞAR T. Network Security: A Decision and Game-Theoretic Approach[M]. Cambridge: Cambridge University Press, 2010: 20–34. [2] 刘小虎, 张恒巍, 马军强, 等. 基于攻防博弈的网络防御决策方法研究综述[J]. 网络与信息安全学报, 2022, 8(1): 1–14. doi: 10.11959/j.issn.2096-109x.2021089LIU Xiaohu, ZHANG Hengwei, MA Junqiang, et al. Research review of network defense decision-making methods based on attack and defense game[J]. Chinese Journal of Network and Information Security, 2022, 8(1): 1–14. doi: 10.11959/j.issn.2096-109x.2021089 [3] DO C T, TRAN N H, HONG C, et al. Game theory for cyber security and privacy[J]. ACM Computing Surveys, 2018, 50(2): 30. doi: 10.1145/3057268 [4] 黄健明, 张恒巍, 王晋东, 等. 基于攻防演化博弈模型的防御策略选取方法[J]. 通信学报, 2017, 38(1): 168–176. doi: 10.11959/j.issn.1000-436x.2017019HUANG Jianming, ZHANG Hengwei, WANG Jindong, et al. Defense strategies selection based on attack-defense evolutionary game model[J]. Journal on Communications, 2017, 38(1): 168–176. doi: 10.11959/j.issn.1000-436x.2017019 [5] SANDHOLM W H. Evolutionary game theory[M]. SOTOMAYOR M, PÉREZ-CASTRILLO D, and CASTIGLIONE F. Complex Social and Behavioral Systems. New York: Springer, 2020: 573–608. [6] 蒋侣, 张恒巍, 王晋东. 基于多阶段Markov信号博弈的移动目标防御最优决策方法[J]. 电子学报, 2021, 49(3): 527–535. doi: 10.12263/DZXB.20191070JIANG Lv, ZHANG Hengwei, and WANG Jindong. A markov signaling game-theoretic approach to moving target defense strategy selection[J]. Acta Elctronica Sinica, 2021, 49(3): 527–535. doi: 10.12263/DZXB.20191070 [7] SHAMMA J S and ARSLAN G. Dynamic fictitious play, dynamic gradient play, and distributed convergence to Nash equilibria[J]. IEEE Transactions on Automatic Control, 2005, 50(3): 312–327. doi: 10.1109/TAC.2005.843878 [8] MASSAQUOI S G. Modeling the function of the cerebellum in scheduled linear servo control of simple horizontal planar arm movements[D]. [Ph. D. dissertation], Massachusetts Institute of Technology, 1999. [9] 林旺群, 王慧, 刘家红, 等. 基于非合作动态博弈的网络安全主动防御技术研究[J]. 计算机研究与发展, 2011, 48(2): 306–316.LIN Wangqun, WANG Hui, LIU Jiahong, et al. Research on active defense technology in network security based on non-cooperative dynamic game theory[J]. Journal of Computer Research and Development, 2011, 48(2): 306–316. [10] WANG Kun, DU Miao, YANG Dejun, et al. Game-theory-based active defense for intrusion detection in cyber-physical embedded systems[J]. ACM Transactions on Embedded Computing Systems, 2016, 16(1): 1–21. doi: 10.1145/2886100 [11] 王增光, 卢昱, 李玺. 基于不完全信息博弈的军事信息网络主动防御策略选取[J]. 兵工学报, 2020, 41(3): 608–617. doi: 10.3969/j.issn.1000-1093.2020.03.022WANG Zengguang, LU Yu, and LI Xi. Active defense strategy selection of military information network based on incomplete information game[J]. Acta Armamentarii, 2020, 41(3): 608–617. doi: 10.3969/j.issn.1000-1093.2020.03.022 [12] SUN Yan, LIN Fuhong, and ZHANG Nan. A security mechanism based on evolutionary game in fog computing[J]. Saudi Journal of Biological Sciences, 2018, 25(2): 237–241. doi: 10.1016/j.sjbs.2017.09.010 [13] 杨峻楠, 张红旗, 张传富. 基于随机博弈与改进WoLF-PHC的网络防御决策方法[J]. 计算机研究与发展, 2019, 56(5): 942–954. doi: 10.7544/issn1000-1239.2019.20180877YANG Junnan, ZHANG Hongqi, and ZHANG Chuanfu. Network defense decision-making method based on stochastic game and improved WoLF-PHC[J]. Journal of Computer Research and Development, 2019, 56(5): 942–954. doi: 10.7544/issn1000-1239.2019.20180877 [14] DU Jun, JIANG Chunxiao, CHEN K C, et al. Community-structured evolutionary game for privacy protection in social networks[J]. IEEE Transactions on Information Forensics and Security, 2018, 13(3): 574–589. doi: 10.1109/TIFS.2017.2758756 [15] 黄健明, 张恒巍. 基于改进复制动态演化博弈模型的最优防御策略选取[J]. 通信学报, 2018, 39(1): 170–182. doi: 10.11959/j.issn.1000-436x.2018010HUANG Jianming and ZHANG Hengwei. Improving replicator dynamic evolutionary game model for selecting optimal defense strategies[J]. Journal on Communications, 2018, 39(1): 170–182. doi: 10.11959/j.issn.1000-436x.2018010 [16] 黄健明, 张恒巍. 基于随机演化博弈模型的网络防御策略选取方法[J]. 电子学报, 2018, 46(9): 2222–2228. doi: 10.3969/j.issn.0372-2112.2018.09.025HUANG Jianming and ZHANG Hengwei. A Method for selecting defense strategies based on stochastic evolutionary game model[J]. Acta Electronica Sinica, 2018, 46(9): 2222–2228. doi: 10.3969/j.issn.0372-2112.2018.09.025 [17] YANG Yu, CHE Bichen, ZENG Yang, et al. MAIAD: A Multistage asymmetric information attack and defense model based on evolutionary game theory[J]. Symmetry, 2019, 11(2): 215. doi: 10.3390/sym11020215 [18] 刘江, 张红旗, 刘艺. 基于不完全信息动态博弈的动态目标防御最优策略选取研究[J]. 电子学报, 2018, 46(1): 82–89. doi: 10.3969/j.issn.0372-2112.2018.01.012LIU Jiang, ZHANG Hongqi, and LIU Yi. Research on optimal selection of moving target defense policy based on dynamic game with incomplete information[J]. Acta Electronica Sinica, 2018, 46(1): 82–89. doi: 10.3969/j.issn.0372-2112.2018.01.012 [19] 张恩宁, 王刚, 马润年, 等. 采用双异质群体演化博弈的网络安全防御决策方法[J]. 西安交通大学学报, 2021, 55(9): 178–188. doi: 10.7652/xjtuxb202109020ZHANG Enning, WANG Gang, MA Runnian, et al. Network security defense decision making method based on dual heterogeneous population evolutionary game model[J]. JOurnal of Xi’an Jiaotong University, 2021, 55(9): 178–188. doi: 10.7652/xjtuxb202109020 [20] 王刚, 王志屹, 张恩宁, 等. 多阶段平台动态防御的Markov演化博弈模型及迁移策略[J]. 兵工学报, 2021, 42(8): 1690–1697. doi: 10.3969/j.issn.1000-1093.2021.08.013WANG Gang, WANG Zhiyi, ZHANG Enning, et al. Markov evolutionary game model and migration strategies for multi-stage platform dynamic defense[J]. Acta Armamentarii, 2021, 42(8): 1690–1697. doi: 10.3969/j.issn.1000-1093.2021.08.013 [21] 姜伟, 方滨兴, 田志宏, 等. 基于攻防博弈模型的网络安全测评和最优主动防御[J]. 计算机学报, 2009, 32(4): 817–827. doi: 10.3724/SP.J.1016.2009.00817JIANG Wei, FANG Binxing, TIAN Zhihong, et al. Evaluating network security and optimal active defense based on attack-defense game model[J]. Chinese Journal of Computers, 2009, 32(4): 817–827. doi: 10.3724/SP.J.1016.2009.00817 [22] HU Hao, LIU Yuling, CHEN Chen, et al. Optimal decision making approach for cyber security defense using evolutionary game[J]. IEEE Transactions on Network and Service Management, 2020, 17(3): 1683–1700. doi: 10.1109/tnsm.2020.2995713 -







 下载:
下载:






 下载:
下载:
