一种抑制相位噪声的多通道变时延下变频全双工收发方法

全欣; 刘颖; 范平志; 唐友喜

doi:10.11999/JEIT220464

一种抑制相位噪声的多通道变时延下变频全双工收发方法

doi: 10.11999/JEIT220464

全欣^1, ,,
刘颖²,
范平志¹,
唐友喜²

1.
西南交通大学信息与科学技术学院成都 611756
2.
电子科技大学通信抗干扰技术国家级重点实验室成都 611731

基金项目: 国家自然科学基金(61901396, 62071094, 62020106001)，四川省自然科学基金(2022NSFSC0879, 2022NSFSC0910)，高等学校学科创新引智计划 (111-2-14)

详细信息

作者简介:
全欣：女，助理研究员，研究方向为全双工通信、自干扰抑制、相位噪声抑制、非线性校正

刘颖：男，副教授，研究方向为非线性数字信号处理、全双工通信、无线通信信号处理

范平志：男，教授，研究方向为高移动性宽带无线通信、信号设计与处理、信息理论与编码、无线频谱资源管理

唐友喜：男，教授，研究方向为无线通信系统、抗干扰与安全通信系统、机器学习与人工智能

通讯作者:
全欣　15881069748@139.com

中图分类号: TN92
计量
- 文章访问数: 379
- HTML全文浏览量: 172
- PDF下载量: 74
- 被引次数: 0
出版历程
- 收稿日期: 2022-04-18
- 修回日期: 2022-08-03
- 网络出版日期: 2022-08-08
- 刊出日期: 2023-05-10

A Multiple-downconversion Full-Duplex Transceiver Receiver Design for Phase Noise Suppression

1.
School of Information Science and Technology, Southwest Jiaotong University, Chengdu 611756, China
2.
National Key Laboratory of Science and Technology on Communications, University of Electronic Science and Technology of China, Chengdu 611731, China

Funds: The National Natural Science Foundation of China (61901396, 62071094, 62020106001), The Natural Science Foundation of Sichuan Province (2022NSFSC0879, 2022NSFSC0910), The Program of Introducing Talents of Discipline to Universities (111-2-14)

摘要

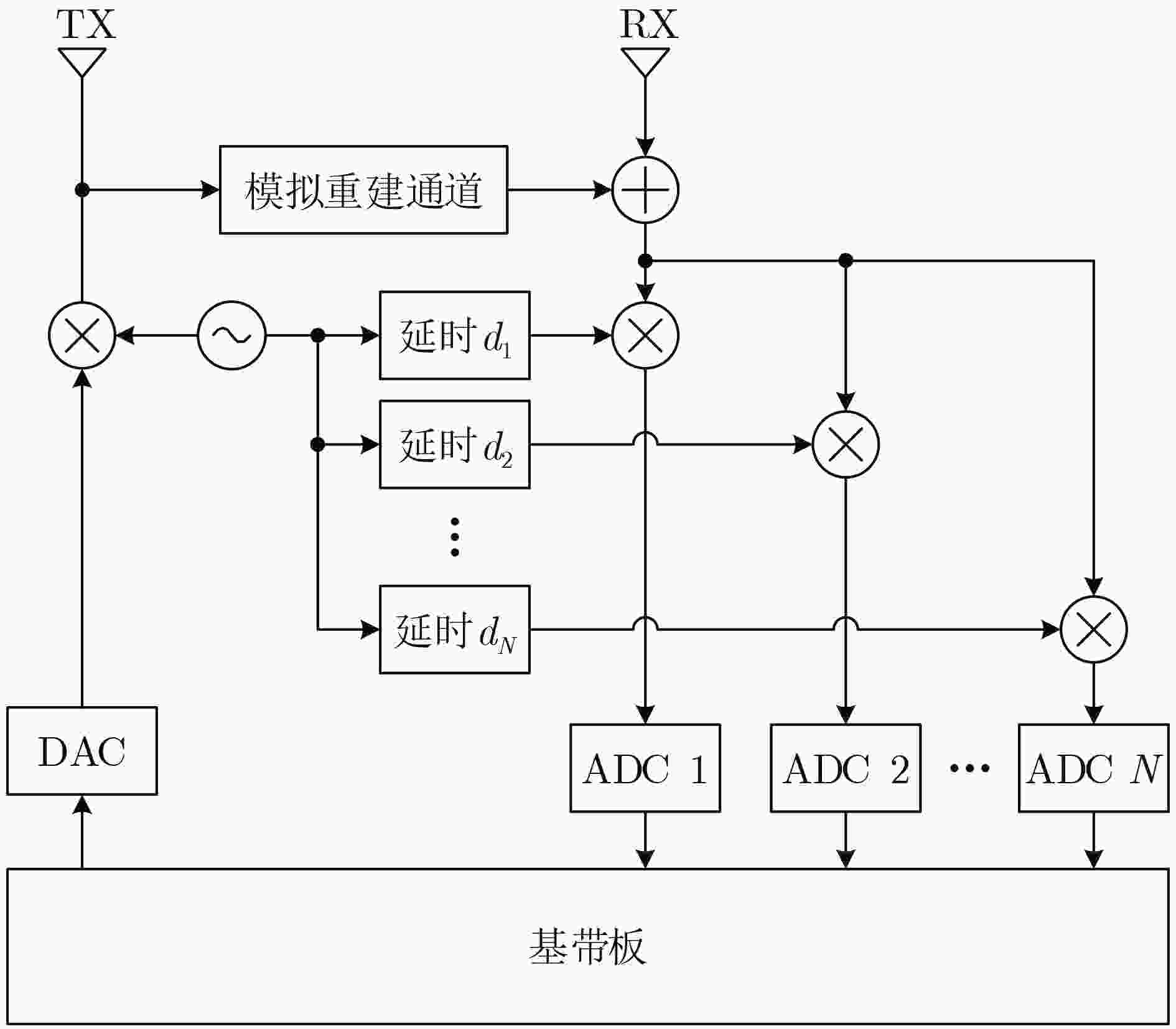
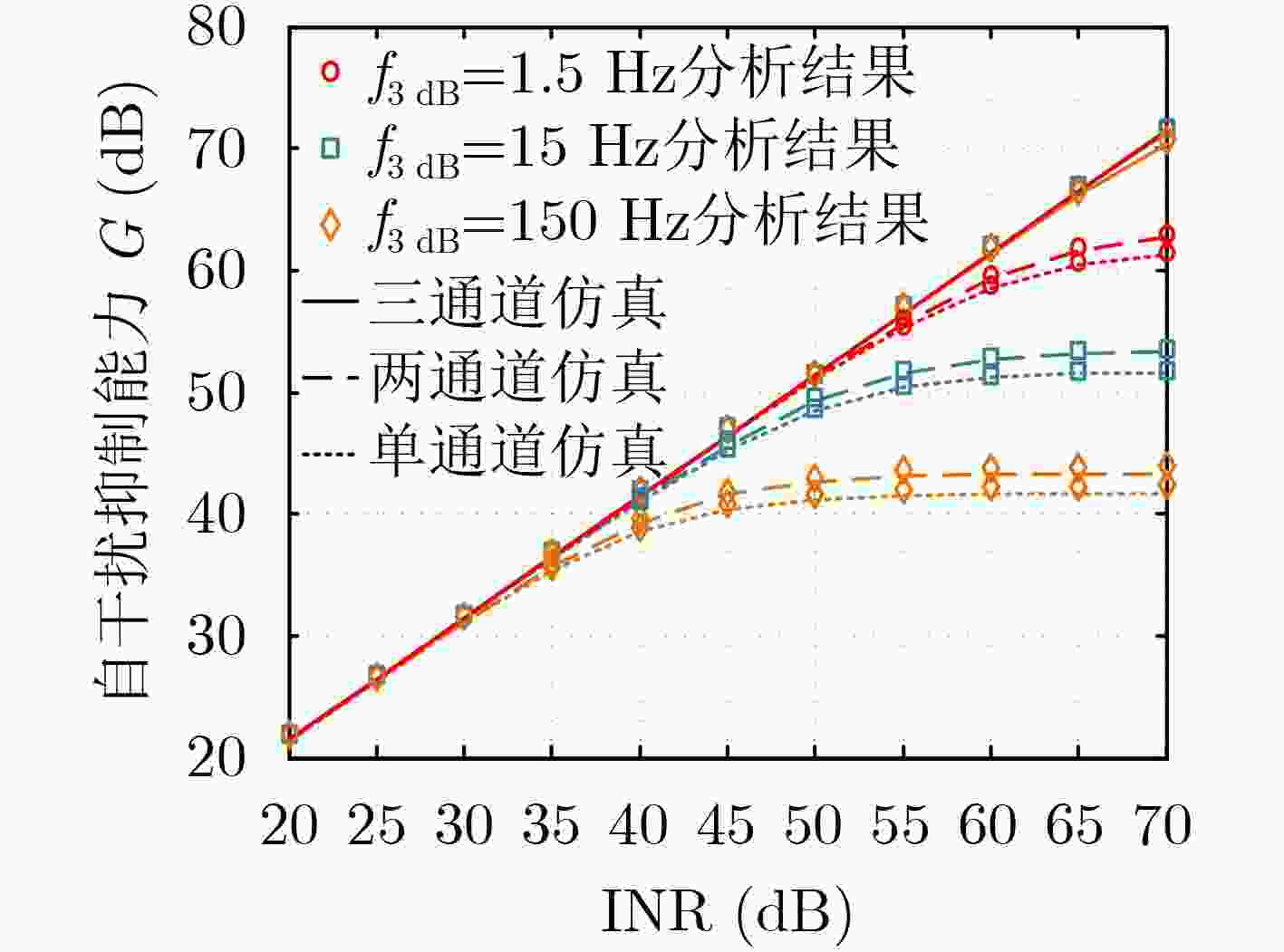
摘要: 相位噪声会限制全双工(FD)收发机的自干扰抑制能力，恶化有用信号解调性能，即使全双工收发机采用发射机、接收机共用本振的结构，也无法消除相位噪声的限制作用。为了降低多径自干扰(SI)分量中相位噪声的影响，该文提出一种多通道变时延下变频全双工收发方法，具体包括可以补偿相位噪声的全双工收发机设计和能够抑制残余相位噪声的自干扰抑制算法。多通道变时延下变频全双工收发机采用多条通道接收同一天线的信号，各接收本振信号为经过不同延时调整的发射本振信号，可以在下变频时补偿多径自干扰中的相位噪声。自干扰抑制算法利用不同接收信号估计相位噪声参数，进一步降低残余相位噪声的影响。此外，该文推导了这种全双工收发方法的自干扰抑制能力，并给出了其随发射功率、接收通道数量的变化关系。分析与仿真结果表明，当接收通道数量高于自干扰信道强径数量时，多通道变时延下变频全双工接收方法不受相位噪声影响。
- 全双工 /
- 相位噪声 /
- 自干扰抑制
Abstract: Phase noise limits the cancellation capability of a Full-Duplex (FD) transceiver receiver and degrades the demodulation performance of the signal-of-interest, even for the transceiver receiver which deploy one common oscillator for its transmitter and its receiver. In order to mitigate the phase noises contained in the multipath Self-Interference (SI) components, a multiple-downconversion FD transceiver receiver design is proposed to suppress these phase noises. The proposed multiple-downconversion FD transceiver receiver design includes a new FD transceiver architecture with multiple receive chains, and a phase noise cancellation algorithm. The FD transceiver architecture deploys multiple receive chains to downconvert the signal received by one antenna. Particularly, the oscillator signal of each receive chain is originated from the transmit oscillator with a unique delay, such that the phase noises contained in the multipath SI components can be compensated. The phase noise cancellation algorithm deploys the received signals in different receive chains to estimate the phase noise coefficients, which can cancel the residual phase noise after the multiple-downconversion. The cancellation capability of the cancellation algorithm is derived and analyzed. Analytical and simulation results demonstrate that, in the scenario that the number of receive chains is greater than the number of strong multiple SI components, the phase noise does not affect the cancellation capability of proposed FD transceiver.
- Full-Duplex(FD) /
- Phase noise /
- Self-Interference(SI) cancellation

HTML全文

图 1 多通道变时延下变频全双工收发机

下载: 全尺寸图片幻灯片

图 2 多通道变时延下变频接收机在不同相位噪声条件下的自干扰抑制能力

下载: 全尺寸图片幻灯片

图 3 多通道变时延下变频接收机在不同信道条件下的自干扰抑制能力

下载: 全尺寸图片幻灯片

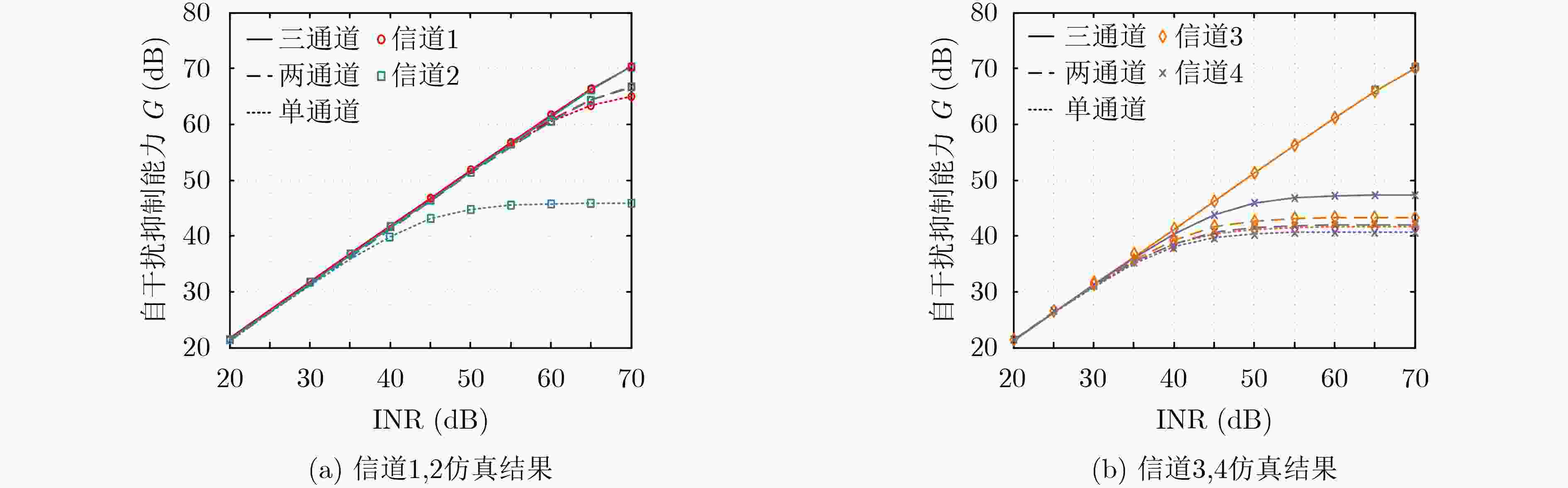
表 1 自干扰信道参数设置(dB)

多径延时(采样点)
0 3 5 8

信道1功率 0 –30 –35 –40
信道2功率 0 –5 –35 –40
信道3功率 0 –5 –8 –40
信道4功率 0 –5 –8 –10

下载: 导出CSV

参考文献(19)

[1]	SABHARWAL A, SCHNITER P, GUO Dongning, et al. In-band full-duplex wireless: Challenges and opportunities[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(9): 1637–1652. doi: 10.1109/JSAC.2014.2330193
[2]	陈慧, 张铭宇, 李兴旺, 等. I/Q失衡影响下无人机多向全双工中继NOMA传输系统性能分析[J]. 电子与信息学报, 2022, 44(3): 987–995. doi: 10.11999/JEIT211020 CHEN Hui, ZHANG Mingyu, LI Xingwang, et al. Performances analysis in UAV-aided multi-way NOMA full-duplex relay system with I/Q imbalance[J]. Journal of Electronics &Information Technology, 2022, 44(3): 987–995. doi: 10.11999/JEIT211020
[3]	刘毅, 吴炯, 杨普, 等. 面向OFDM的同时同频全双工双向高谱效中继方案[J]. 电子与信息学报, 2019, 41(2): 402–408. doi: 10.11999/JEIT180451 LIU Yi, WU Jiong, YANG Pu, et al. High spectrum efficiency full-duplex two-way relay scheme for OFDM[J]. Journal of Electronics &Information Technology, 2019, 41(2): 402–408. doi: 10.11999/JEIT180451
[4]	HE Yimin, ZHAO Mengyun, GUO Wenbo, et al. Performance analysis of nonlinear self-interference cancellation with timing error in full-duplex systems[J]. IEEE Wireless Communications Letters, 2021, 10(5): 1075–1078. doi: 10.1109/LWC.2021.3057893
[5]	徐强, 全欣, 潘文生, 等. 同时同频全双工LTE射频自干扰抑制能力分析及实验验证[J]. 电子与信息学报, 2014, 36(3): 662–668. doi: 10.3724/SP.J.1146.2013.00717 XU Qiang, QUAN Xin, PAN Wensheng, et al. Analysis and experimental verification of RF self-interference cancelation for Co-time Co-frequency full-duplex LTE[J]. Journal of Electronics &Information Technology, 2014, 36(3): 662–668. doi: 10.3724/SP.J.1146.2013.00717
[6]	KIM D, LEE H, and HONG D. A survey of in-band full-duplex transmission: From the perspective of PHY and MAC layers[J]. IEEE Communications Surveys & Tutorials, 2015, 17(4): 2017–2046. doi: 10.1109/COMST.2015.2403614
[7]	QUAN Xin, LIU Ying, SHAO Shihai, et al. Impacts of phase noise on digital self-interference cancellation in full-duplex communications[J]. IEEE Transactions on Signal Processing, 2017, 65(7): 1881–1893. doi: 10.1109/TSP.2017.2652384
[8]	SAHAI A, PATEL G, DICK C, et al. On the impact of phase noise on active cancelation in wireless full-duplex[J]. IEEE Transactions on Vehicular Technology, 2013, 62(9): 4494–4510. doi: 10.1109/TVT.2013.2266359
[9]	SYRJALA V, VALKAMA M, ANTTILA L, et al. Analysis of oscillator phase-noise effects on self-interference cancellation in full-duplex OFDM radio transceivers[J]. IEEE Transactions on Wireless Communications, 2014, 13(6): 2977–2990. doi: 10.1109/TWC.2014.041014.131171
[10]	AHMED E, ELTAWIL A M, and SABHARWAL A. Self-interference cancellation with phase noise induced ICI suppression for full-duplex systems[C]. IEEE Global Communications Conference (GLOBECOM), Atlanta, USA, 2013: 3384–3388.
[11]	AHMED E and ELTAWIL A M. On phase noise suppression in full-duplex systems[J]. IEEE Transactions on Wireless Communications, 2015, 14(3): 1237–1251. doi: 10.1109/TWC.2014.2365536
[12]	SHEHATA H and KHATTAB T. Self-interference cancellation using time-domain phase noise estimation in OFDM full-duplex systems[C]. 13th International Wireless Communications and Mobile Computing Conference, Valencia, Spain, 2017: 293–298.
[13]	SYRJAELAE V and YAMAMOTO K. Self-interference cancellation in full-duplex radio transceivers with oscillator phase noise[C]. 20th European Wireless Conference, Barcelona, Spain, 2014: 1–6.
[14]	PAN Yulong, ZHOU Cheng, CUI Gaofeng, et al. Self-interference cancellation with RF impairments suppression for full-duplex systems[C]. IEEE 82nd Vehicular Technology Conference (VTC Fall), Boston, USA, 2015: 1–5.
[15]	MASMOUDI A and LE-NGOC T. A maximum-likelihood channel estimator in MIMO full-duplex systems[C]. IEEE 80th Vehicular Technology Conference, Vancouver, Canada, 2014: 1–5.
[16]	LI Ruozhu, MASMOUDI A, and LE-NGOC T. Self-interference cancellation with nonlinearity and phase-noise suppression in full-duplex systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(3): 2118–2129. doi: 10.1109/TVT.2017.2754489
[17]	QUAN Xin, PAN Wensheng, LIU Ying, et al. Phase noise mitigation architecture for wireless full-duplex transceivers[J]. Electronics Letters, 2018, 54(24): 1407–1409. doi: 10.1049/el.2018.5684
[18]	QUAN Xin, LIU Ying, FAN Pingzhi, et al. Full-duplex transceiver design in the presence of phase noise and performance analysis[J]. IEEE Transactions on Vehicular Technology, 2021, 70(1): 558–571. doi: 10.1109/TVT.2020.3047076
[19]	PETROVIC D, RAVE W, and FETTWEIS G. Effects of phase noise on OFDM systems with and without PLL: Characterization and compensation[J]. IEEE Transactions on Communications, 2007, 55(8): 1607–1616. doi: 10.1109/TCOMM.2007.902593