Multiple Parameters Weighted-type FRactional Fourier Transform Secure Communication Method Based on Cosine Power-Activation Discrete Hyperchaotic Encryption
-
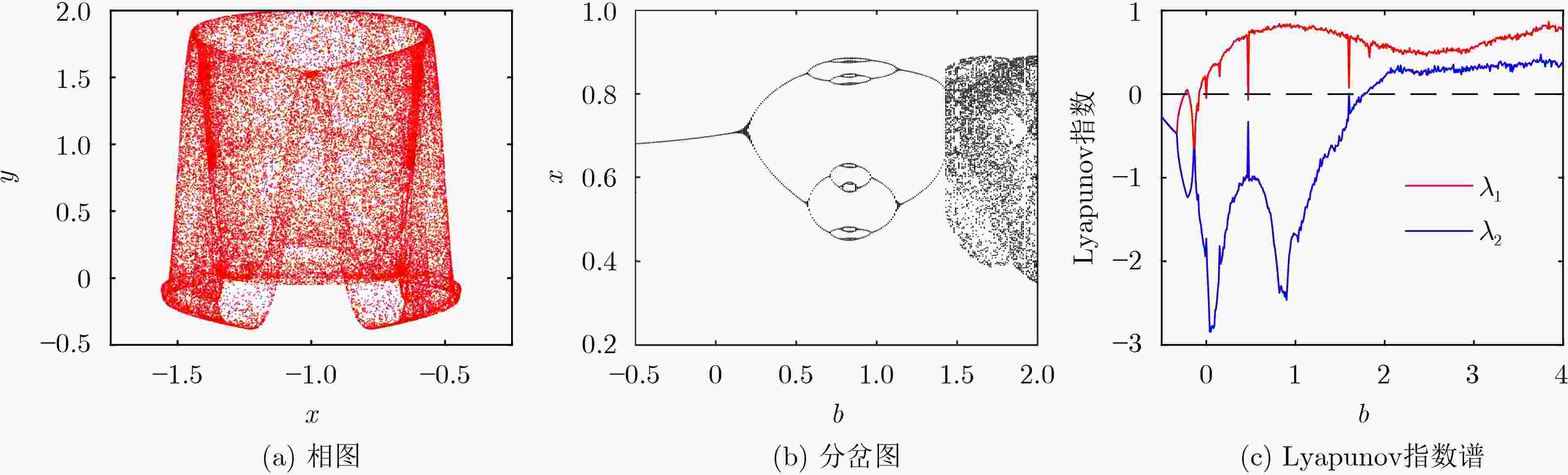
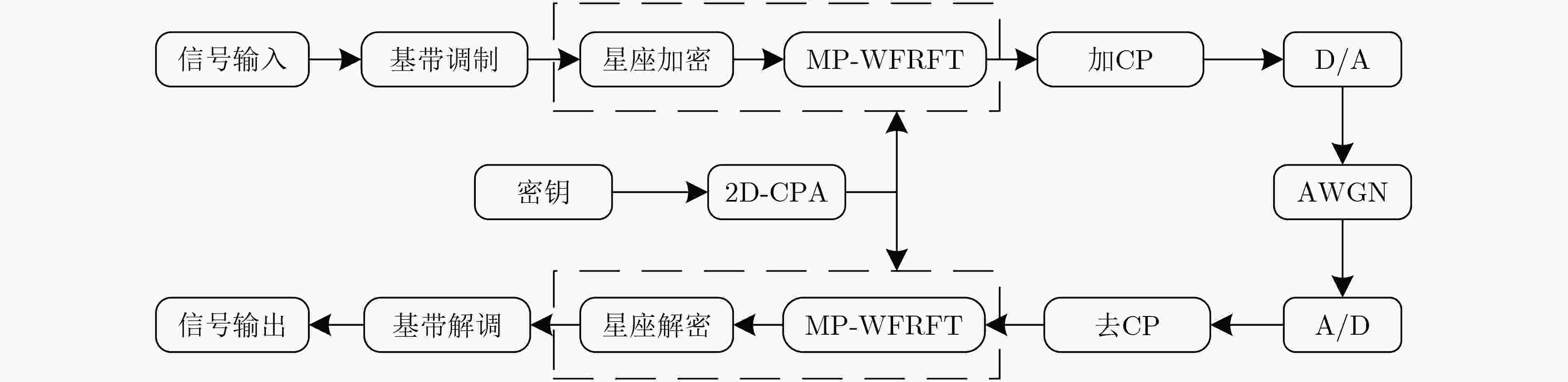
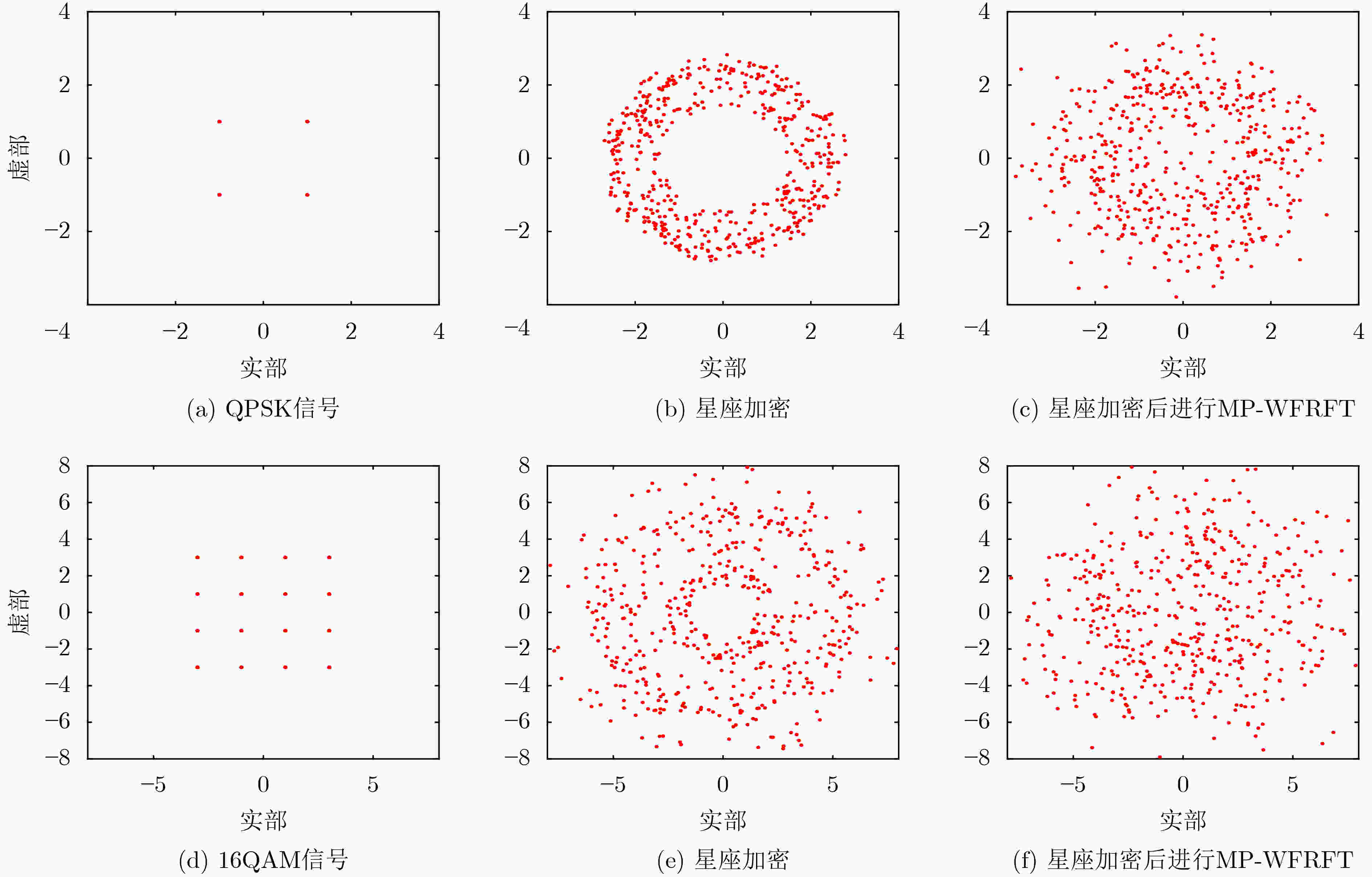
摘要: 为提高物理层安全传输性能,该文提出一种新的基于2维余幂-激活(2D-CPA)离散超混沌加密的多参数加权分数傅里叶变换(MP-WFRFT)安全通信方法。首先,将激活函数和余弦函数作为非线性因子引入1维立方(cubic)混沌映射,构造2维混沌映射。非线性因子可对原始cubic混沌映射的迭代过程进行扰动,从而获得更加饱满的相轨。利用分岔图、相图、Lyapunov指数谱等对提出的2维混沌映射动力学特性进行了验证。结果表明,构造的2维混沌序列随机性良好,可进入超混沌状态。然后,利用余幂-激活离散超混沌序列分别构建幅度变换矩阵、相位旋转矩阵和MP-WFRFT参数池,完成对星座幅相加密,以及MP-WFRFT动态变换加密过程,进一步消除数据统计特征,同时提升MP-WFRFT变换的抗参数扫描性能。数值仿真结果表明,加密数据的星座图呈类高斯分布,且传输系统对密钥的敏感性良好。
-
关键词:
- 2维离散超混沌 /
- 星座加密 /
- 多参数加权分数傅里叶变换 /
- Lyapunov指数
Abstract: To improve the secure transmission performance of physical layer, a novel Multiple Parameters Weighted-type FRactional Fourier Transform (MP-WFRFT) secure communication method based on Two-Dimensional Cosine Power-Activation (2D-CPA) discrete hyperchaotic encryption is proposed. Firstly, the activation function and cosine function are introduced into the one-dimensional cubic chaos map as nonlinear factors to construct the 2D chaos map. The nonlinear factor can perturb the iterative process of the original cubic chaotic map so as to obtain a fuller phase orbit. The dynamic characteristics of the proposed two-dimensional chaotic mapping are verified by using bifurcation diagram, phase diagram and Lyapunov exponential spectrum. The results show that the constructed 2D chaotic sequence has good randomness and can enter hyperchaotic state. Then, the amplitude transformation matrix, phase rotation matrix and MP-WFRFT parameter pool are constructed by using 2D-CPA hyperchaotic sequence respectively to complete the constellation amplitude phase encryption and MP-WFRFT dynamic transformation encryption process, the statistical characteristics of data are further eliminated and the anti-parameter scanning performance of MP-WFRFT transform is improved. Numerical simulation results show that the constellation diagram of the encrypted data is Gaussian-like and that the transmission system is well sensitive to the key. -
表 1 两类混沌映射的Lyapunov指数、ApEn和PE
混沌映射 最大Lyapunov指数 ApEn PE cubic 0.6512 0.6403 0.9290 2D-CPA 0.8054 0.9689 0.9955 表 3 仿真参数
特性 参数 调制方式 QPSK, 16QAM 信道类型 AWGN 分组长度 512 信号长度 262144 -
[1] WEN Shiping, ZENG Zhigang, HUANG Tingwen, et al. Lag synchronization of switched neural networks via neural activation function and applications in image encryption[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(7): 1493–1502. doi: 10.1109/TNNLS.2014.2387355 [2] HU Xiaonan, YANG Xuelin, SHEN Zanwei, et al. Chaos-based partial transmit sequence technique for physical layer security in OFDM-PON[J]. IEEE Photonics Technology Letters, 2015, 27(23): 2429–2432. doi: 10.1109/LPT.2015.2466092 [3] MATTHEWS R. On the derivation of a “Chaotic” encryption algorithm[J]. Cryptologia, 1989, 13(1): 29–42. doi: 10.1080/0161-118991863745 [4] ARIF J, KHAN M A, GHALEB B, et al. A novel chaotic permutation-substitution image encryption scheme based on logistic map and random substitution[J]. IEEE Access, 2022, 10: 12966–12982. doi: 10.1109/ACCESS.2022.3146792 [5] 黄冬梅, 耿霞, 魏立斐, 等. 基于Henon映射的加密遥感图像的安全检索方案[J]. 软件学报, 2016, 27(7): 1729–1740. doi: 10.13328/j.cnki.jos.005039HUANG Dongmei, GENG Xia, WEI Lifei, et al. A secure query scheme on encrypted remote sensing images based on Henon mapping[J]. Journal of Software, 2016, 27(7): 1729–1740. doi: 10.13328/j.cnki.jos.005039 [6] ALI T S and ALI R. A novel medical image signcryption scheme using TLTS and Henon chaotic map[J]. IEEE Access, 2020, 8: 71974–71992. doi: 10.1109/ACCESS.2020.2987615 [7] GILL H S, GILL S S, and BHATIA K S. A novel chaos-based encryption approach for future-generation passive optical networks using SHA-2[J]. Journal of Optical Communications and Networking, 2017, 9(12): 1184–1190. doi: 10.1364/JOCN.9.001184 [8] LIU Fang. WFRFT secure communication method based on chaotic parameter pool[J]. Mathematical Problems in Engineering, 2019, 2019: 1265930. doi: 10.1155/2019/1265930 [9] ZHANG Lijia, XIN Xiangjun, LIU Bo, et al. Secure OFDM-PON based on chaos scrambling[J]. IEEE Photonics Technology Letters, 2011, 23(14): 998–1000. doi: 10.1109/LPT.2011.2149512 [10] 岳敖, 李为, 马东堂, 等. 拉丁阵和幅相变换相结合的物理层加密传输算法[J]. 信号处理, 2016, 32(6): 660–668. doi: 10.16798/j.issn.1003-0530.2016.06.004YUE Ao, LI Wei, MA Dongtang, et al. A novel physical layer encryption algorithm combined Latin rectangle and phase-amplitude mask[J]. Journal of Signal Processing, 2016, 32(6): 660–668. doi: 10.16798/j.issn.1003-0530.2016.06.004 [11] HU Zhouyi and CHAN C K. A 7-D hyperchaotic system-based encryption scheme for secure fast-OFDM-PON[J]. Journal of Lightwave Technology, 2018, 36(16): 3373–3381. doi: 10.1109/JLT.2018.2841042 [12] LIU Zhentao, WU Chunxiao, WANG Jun, et al. A color image encryption using dynamic DNA and 4-D memristive hyper-chaos[J]. IEEE Access, 2019, 7: 78367–78378. doi: 10.1109/ACCESS.2019.2922376 [13] SUN Shuliang. A novel hyperchaotic image encryption scheme based on DNA encoding, pixel-level scrambling and bit-level scrambling[J]. IEEE Photonics Journal, 2018, 10(2): 7201714. doi: 10.1109/JPHOT.2018.2817550 [14] SULTAN A, YANG Xuelin, HAJOMER A A E, et al. Chaotic distribution of QAM symbols for secure OFDM signal transmission[J]. Optical Fiber Technology, 2019, 47: 61–65. doi: 10.1016/j.yofte.2018.11.022 [15] 刘思聪, 李春彪, 李泳新. 基于指数-余弦离散混沌映射的图像加密算法研究[J]. 电子与信息学报, 2022, 44(5): 1754–1762. doi: 10.11999/JEIT210270LIU Sicong, LI Chunbiao, and LI Yongxin. A novel image encryption algorithm based on exponent-cosine chaotic mapping[J]. Journal of Electronics &Information Technology, 2022, 44(5): 1754–1762. doi: 10.11999/JEIT210270 [16] 李春彪, 赵云楠, 李雅宁, 等. 基于正弦反馈Logistic混沌映射的图像加密算法及其FPGA实现[J]. 电子与信息学报, 2021, 43(12): 3766–3774. doi: 10.11999/JEIT200575LI Chunbiao, ZHAO Yunnan, LI Yaning, et al. An image encryption algorithm based on logistic chaotic mapping with sinusoidal feedback and its FPGA implementation[J]. Journal of Electronics &Information Technology, 2021, 43(12): 3766–3774. doi: 10.11999/JEIT200575 [17] 蒋东华, 朱礼亚, 沈子懿, 等. 结合二维压缩感知和混沌映射的双图像视觉安全加密算法[J]. 西安交通大学学报, 2022, 56(2): 139–148. doi: 10.7652/xjtuxb202202015JIANG Donghua, ZHU Liya, SHEN Ziyi, et al. A double image visual security encryption algorithm combining 2D compressive sensing and chaotic mapping[J]. Journal of Xi'an Jiaotong University, 2022, 56(2): 139–148. doi: 10.7652/xjtuxb202202015 [18] FANG Xiaojie, SHA Xuejun, and LI Yue. MP-WFRFT and constellation scrambling based physical layer security system[J]. China Communications, 2016, 13(2): 138–145. [19] 倪磊, 达新宇, 胡航, 等. 基于改进Logistic相位扰码的抗截获通信[J]. 华中科技大学学报:自然科学版, 2019, 47(6): 35–40. doi: 10.13245/j.hust.190607NI Lei, DA Xinyu, HU Hang, et al. Research on anti-interception communication based on improved Logistic phase scrambling[J]. Journal of Huazhong University of Science and Technology:Nature Science Edition, 2019, 47(6): 35–40. doi: 10.13245/j.hust.190607 [20] YUAN Guogang, CHEN Zili, GAO Xijun, et al. Enhancing the security of chaotic direct sequence spread spectrum communication through WFRFT[J]. IEEE Communications Letters, 2021, 25(9): 2834–2838. doi: 10.1109/LCOMM.2021.3096388 [21] 杨振鑫. WFRFT信号参数识别方法研究[D]. [硕士论文], 哈尔滨工业大学, 2020.YANG Zhenxin. Studies on the methods of parameter identification of WFRFT signal[D]. [Master dissertation], Harbin Institute of Technology, 2020. [22] LIU Fang. A cross-hierarchical scanning method based SP-4-WFRFT for digital communication signals[J]. Mathematical Problems in Engineering, 2018, 2018: 6580146. doi: 10.1155/2018/6580146 [23] 肖成龙, 孙颖, 林邦姜, 等. 基于神经网络与复合离散混沌系统的双重加密方法[J]. 电子与信息学报, 2020, 42(3): 687–694. doi: 10.11999/JEIT190213XIAO Chenglong, SUN Ying, LIN Bangjiang, et al. Double encryption method based on neural network and composite discrete chaotic system[J]. Journal of Electronics &Information Technology, 2020, 42(3): 687–694. doi: 10.11999/JEIT190213 [24] ZHANG Wei, ZHANG Chongfu, CHEN Chen, et al. Hybrid chaotic confusion and diffusion for physical layer security in OFDM-PON[J]. IEEE Photonics Journal, 2017, 9(2): 7201010. doi: 10.1109/JPHOT.2017.2683501 [25] KHAN M and MASOOD F. A novel chaotic image encryption technique based on multiple discrete dynamical maps[J]. Multimedia Tools and Applications, 2019, 78(18): 26203–26222. doi: 10.1007/s11042-019-07818-4 [26] ZHANG Wei, ZHANG Chongfu, JIN Wei, et al. Chaos coding-based QAM IQ-encryption for improved security in OFDMA-PON[J]. IEEE Photonics Technology Letters, 2014, 26(19): 1964–1967. doi: 10.1109/LPT.2014.2343616 [27] SHEN Zanwei, YANG Xuelin, HE Hao, et al. Secure transmission of optical DFT-S-OFDM data encrypted by digital chaos[J]. IEEE Photonics Journal, 2016, 8(3): 7904609. doi: 10.1109/JPHOT.2016.2564438 [28] ZHANG Chongfu, ZHANG Wei, CHEN Chen, et al. Physical-enhanced secure strategy for OFDMA-PON using chaos and deoxyribonucleic acid encoding[J]. Journal of Lightwave Technology, 2018, 36(9): 1706–1712. doi: 10.1109/JLT.2018.2789435 [29] SHANNON C E. Communication theory of secrecy systems[J]. The Bell System Technical Journal, 1949, 28(4): 656–715. doi: 10.1002/j.1538-7305.1949.tb00928.x [30] 黄永新, 房宵杰, 沙学军. 基于二维加权分数傅里叶变换的安全传输方法[J]. 哈尔滨工业大学学报, 2022, 54(5): 11–17. doi: 10.11918/202011077HUANG Yongxin, FANG Xiaojie, and SHA Xuejun. A secure transmission method based on two-dimensional weighted fractional Fourier transform[J]. Journal of Harbin Institute of Technology, 2022, 54(5): 11–17. doi: 10.11918/202011077 -






 下载:
下载:


 下载:
下载:
