Off-grid Imaging Method for Computational Microwave Imaging System of Metamaterial Aperture Based on Sparse Bayesian Learning
-
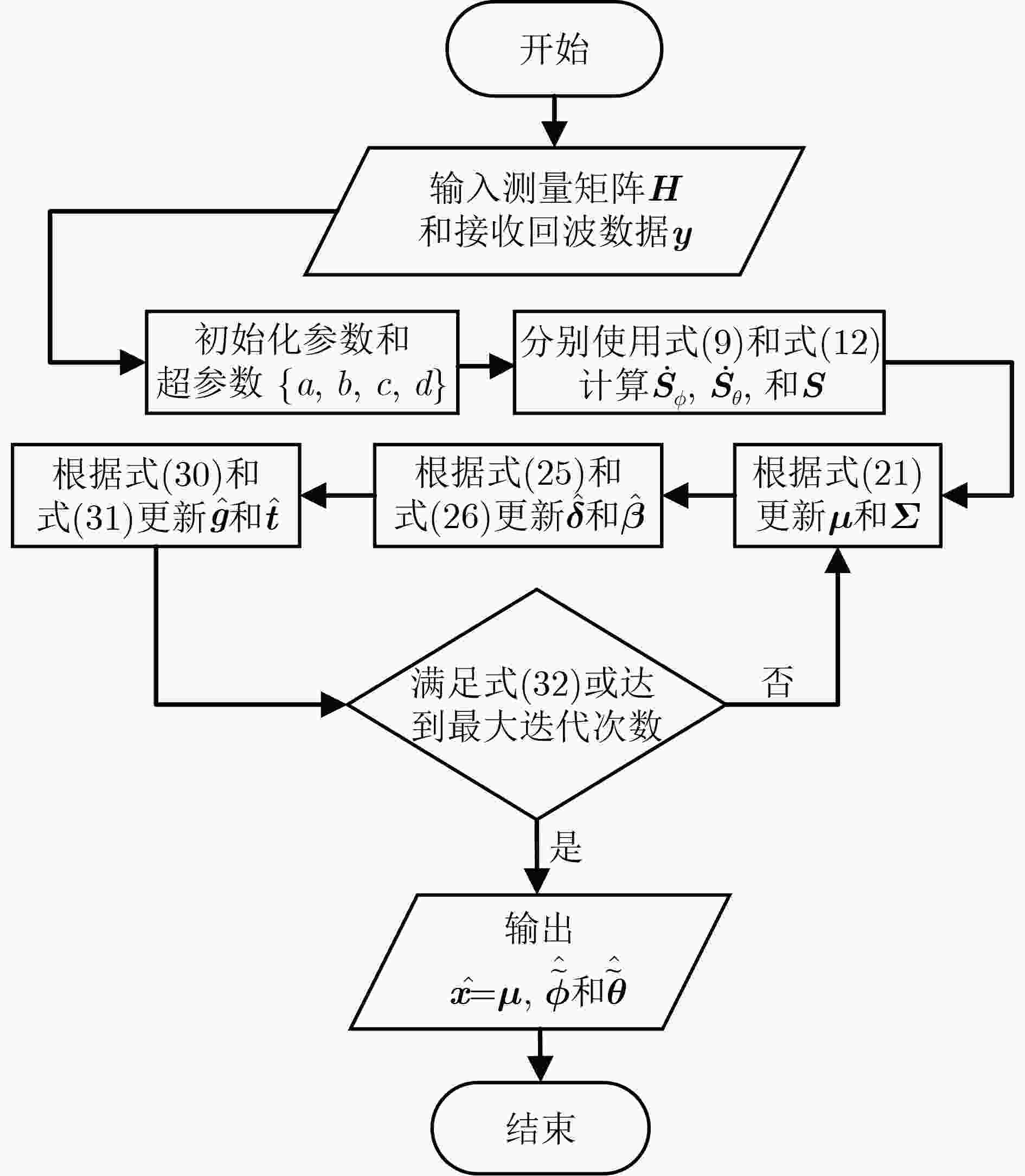
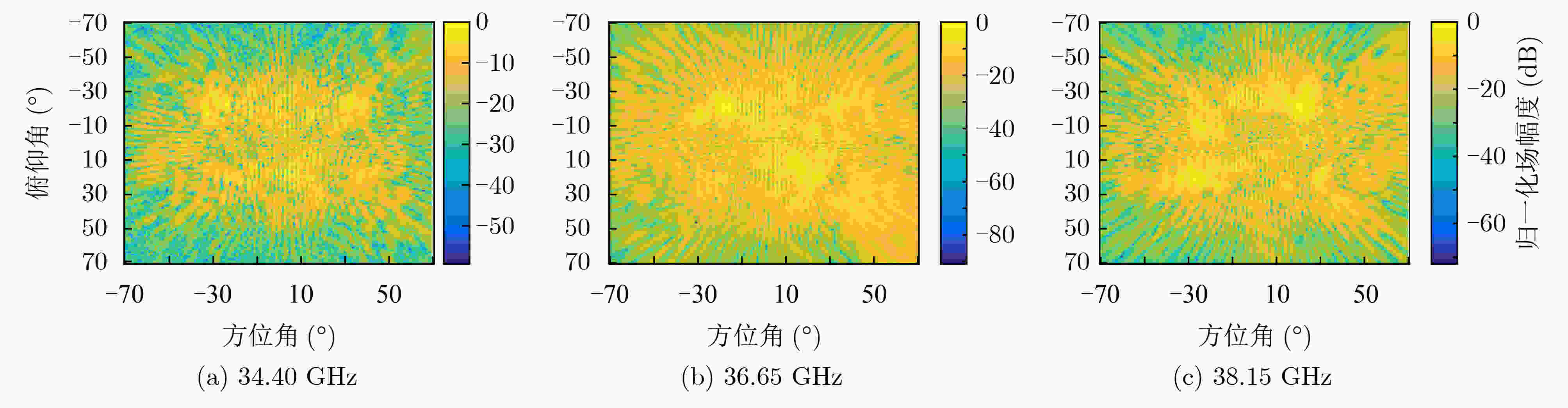
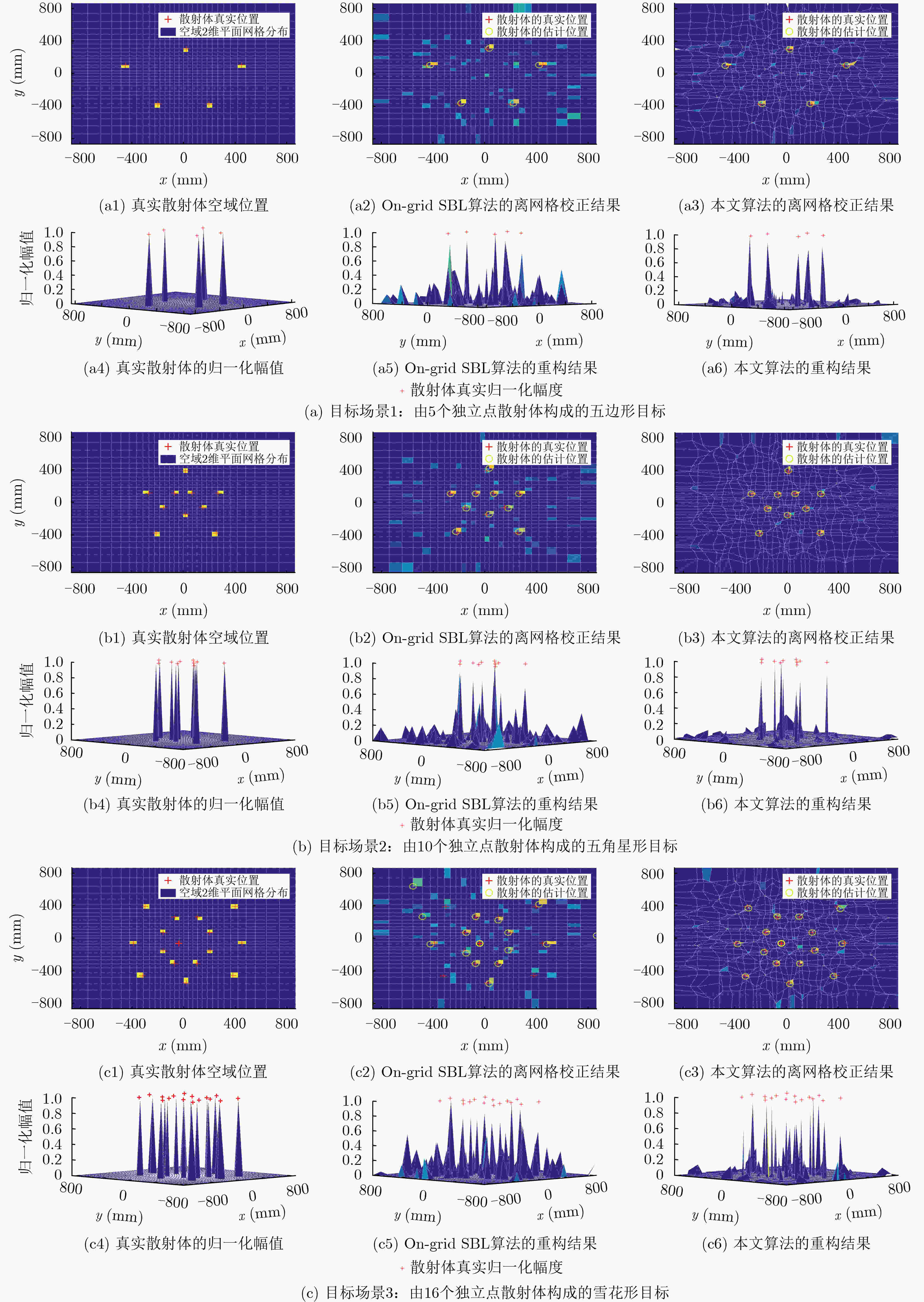
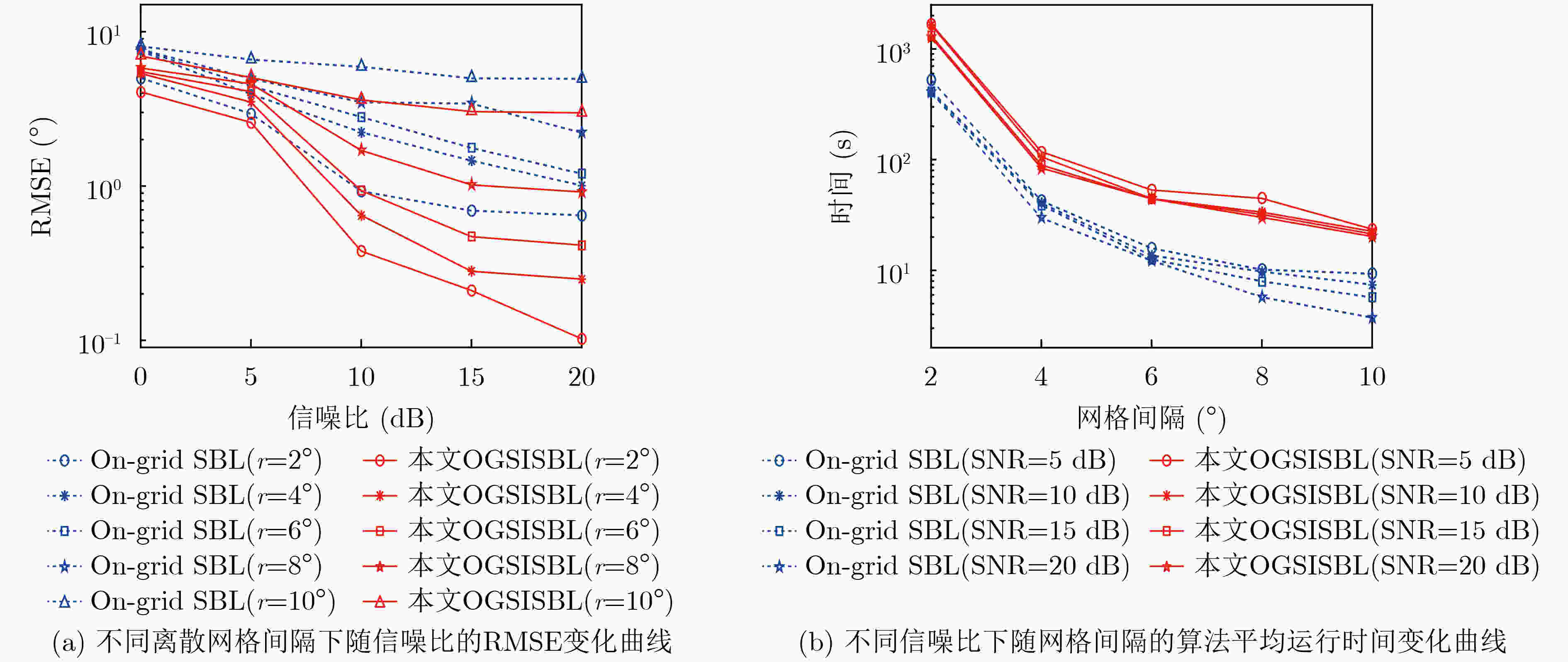
摘要: 基于超材料孔径的计算微波成像可以看作微波压缩感知成像。这种成像方式的成像效果受网格失配误差的严重影响。该文针对超材料孔径计算微波成像系统对2维场景的重构过程进行分析,构建了一种基于Sinc插值函数的2维离网格(Off-grid)观测模型,并在此基础上提出一种基于稀疏贝叶斯学习的Sinc插值离网格成像方法(OGSISBL)。在期望最大化算法的框架下,恢复散射体回波的幅值和位置,同时校准网格失配误差。通过对超材料孔径计算微波成像系统的仿真数据进行成像处理验证所提算法的性能,结果表明所提算法具有很强的鲁棒性。Abstract: Computational microwave imaging based on metamaterial aperture can be considered as microwave compression sensing imaging. The imaging effect of this imaging method is seriously affected by the grid mismatch error. In this paper, a Two-Dimensional (2D) off-grid observation model based on Sinc interpolation function is constructed by analyzing the reconstruction process of 2D scene in the computational microwave imaging system for metamaterial aperture. On this basis, an Off-Grid imaging method using Sinc Interpolation based on Sparse Bayesian Learning (OGSISBL) is proposed. Under the framework of the expectation maximization algorithm, the amplitude and position of the return of the scatterers are recovered, and the off-grid error is calibrated. The performance of the proposed algorithm is verified by imaging the simulation data of the computing microwave imaging system based on metamaterial aperture. The results show that the proposed algorithm has strong robustness.
-
表 1 比较不同信噪比下本文所提算法对散射体位置的重构效果(3种不同场景)(mm)
设置(场景1) SNR=20 dB SNR=15 dB SNR=10 dB SNR=5 dB 平均离网格误差 运行前 运行后 运行前 运行后 运行前 运行后 运行前 运行后 11.00 5.79 11.00 6.13 11.00 7.26 11.00 14.78 设置(场景2) SNR=20 dB SNR=15 dB SNR=10 dB SNR=5 dB 平均离网格误差 运行前 运行后 运行前 运行后 运行前 运行后 运行前 运行后 5.17 2.76 5.17 3.01 5.17 3.94 5.17 9.02 设置(场景3) SNR=20 dB SNR=15 dB SNR=10 dB SNR=5 dB 平均离网格误差 运行前 运行后 运行前 运行后 运行前 运行后 运行前 运行后 5.38 2.86 5.38 3.18 5.38 4.17 5.38 11.09 -
[1] 吴振华. 单通道超材料孔径雷达成像算法研究[D]. [博士论文], 西安电子科技大学, 2019.WU Zhenhua. Research on imaging algorithms of monostatic metamaterial apertures-based radar[D]. [Ph. D. dissertation], Xidian University, 2019. [2] PENG Rixi, YURDUSEVEN O, FROMENTEZE T, et al. Advanced processing of 3D computational microwave polarimetry using a near-field frequency-diverse antenna[J]. IEEE Access, 2020, 8: 166261–166272. doi: 10.1109/ACCESS.2020.3021418 [3] HOANG T V, FUSCO V, FROMENTEZE T, et al. Computational polarimetric imaging using two-dimensional dynamic metasurface apertures[J]. IEEE Open Journal of Antennas and Propagation, 2021, 2: 488–497. doi: 10.1109/OJAP.2021.3069320 [4] SLEASMAN T A, IMANI M F, DIEBOLD A V, et al. Implementation and characterization of a two-dimensional printed circuit dynamic metasurface aperture for computational microwave imaging[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(4): 2151–2164. doi: 10.1109/TAP.2020.3027188 [5] ZHAO Mengran, ZHU Shitao, HUANG Huilin, et al. Frequency-diverse metamaterial cavity antenna for microwave coincidence imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2021, 20(6): 1103–1107. doi: 10.1109/LAWP.2021.3073679 [6] YURDUSEVEN O, GOWDA V R, GOLLUB J N, et al. Printed aperiodic cavity for computational and microwave imaging[J]. IEEE Microwave and Wireless Components Letters, 2016, 26(5): 367–369. doi: 10.1109/LMWC.2016.2548443 [7] ZHAO Mengran, ZHU Shitao, HUANG Huilin, et al. Frequency-diverse metasurface antenna with hybrid bunching methods for coincidence imaging[J]. IEEE Access, 2020, 8: 137711–137719. doi: 10.1109/ACCESS.2020.3012545 [8] LUO Zhenlong, CHENG Yongqiang, CAO Kaicheng, et al. Microwave computational imaging in frequency domain with reprogrammable metasurface[J]. Journal of Electronic Imaging, 2018, 27(6): 063019. doi: 10.1117/1.JEI.27.6.063019 [9] 马彦恒, 侯建强, 李根, 等. 基于方位向信息分离的机动SAR成像算法[J]. 电子与信息学报, 2021, 43(2): 364–371. doi: 10.11999/JEIT190757MA Yanheng, HOU Jianqiang, LI Gen, et al. Maneuvering SAR imaging algorithms based on the separation of azimuthal motion information[J]. Journal of Electronics &Information Technology, 2021, 43(2): 364–371. doi: 10.11999/JEIT190757 [10] 刘新, 阎焜, 杨光耀, 等. UWB-MIMO穿墙雷达三维成像与运动补偿算法研究[J]. 电子与信息学报, 2020, 42(9): 2253–2260. doi: 10.11999/JEIT190356LIU Xin, YAN Kun, YANG Guangyao, et al. Study on 3D imaging and motion compensation algorithm for UWB-MIMO through-wall radar[J]. Journal of Electronics &Information Technology, 2020, 42(9): 2253–2260. doi: 10.11999/JEIT190356 [11] DUARTE M F, DAVENPORT M A, TAKHAR D, et al. Single-pixel imaging via compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 83–91. doi: 10.1109/MSP.2007.914730 [12] YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38–43. doi: 10.1109/TSP.2012.2222378 [13] YOU Kangyong, GUO Wenbin, LIU Yueliang, et al. Grid evolution: Joint dictionary learning and sparse Bayesian recovery for multiple off-grid targets localization[J]. IEEE Communications Letters, 2018, 22(10): 2068–2071. doi: 10.1109/LCOMM.2018.2863374 [14] JAGANNATH R and HARI K V S. Block sparse estimator for grid matching in single snapshot DoA estimation[J]. IEEE Signal Processing Letters, 2013, 20(11): 1038–1041. doi: 10.1109/LSP.2013.2279124 [15] DAI Jisheng, BAO Xu, XU Weichao, et al. Root sparse Bayesian learning for off-grid DOA estimation[J]. IEEE Signal Processing Letters, 2017, 24(1): 46–50. doi: 10.1109/LSP.2016.2636319 [16] WAX M and ADLER A. Direction of arrival estimation in the presence of model errors by signal subspace matching[J]. Signal Processing, 2021, 181: 107900. doi: 10.1016/j.sigpro.2020.107900 [17] FAN Bo, ZHOU Xiaoli, CHEN Shuo, et al. Sparse Bayesian perspective for radar coincidence imaging with model errors[J]. Mathematical Problems in Engineering, 2020, 2020: 9202654. doi: 10.1155/2020/9202654 [18] BURNSIDE W. Aperture antennas and diffraction theory[J]. IEEE Antennas and Propagation Society Newsletter, 1983, 25(1): 21–22. doi: 10.1109/MAP.1983.27664 [19] TZIKAS D G, LIKAS A C, and GALATSANOS N P. The variational approximation for Bayesian inference[J]. IEEE Signal Processing Magazine, 2008, 25(6): 131–146. doi: 10.1109/msp.2008.929620 [20] DAI Fengzhou, ZHANG Shuo, LI Long, et al. Enhancement of metasurface aperture microwave imaging via information-theoretic waveform optimization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5109512. doi: 10.1109/TGRS.2022.3144286 [21] TIPPING M. Sparse Bayesian learning and the relevance vector machine[J]. The Journal of Machine Learning Research, 2001, 1: 211–244. doi: 10.1162/15324430152748236 -





 下载:
下载:



 下载:
下载:
