Elevation Estimation for Airborne Synthetic Aperture Radar Altimetry Based on Parameterized Bayesian Learning
-
摘要: 机载合成孔径雷达高度计(SARA)由于具有高航向分辨率,因此受到广泛关注。然而,现有的SARA地面高程重跟踪方法多基于最小二乘算子,高程参数估计精度和算法抑噪性能均存在上限,容易造成高程参数估计结果过拟合,对复杂高程变化适应能力有限。为此,该文提出一种基于参数化贝叶斯统计学习方法的机载SARA重跟踪算法(PR-Bayes)。通过引入目标场景地形先验概率模型,并结合模型驱动机器学习方法,可实现对目标高程信息重跟踪可信估计,从而有效避免估计参数过拟合问题。该算法基于布朗模型(BM)对SARA回波进行复杂模型参数反演,并设计哈密顿蒙特卡洛(HMC)统计采样器,实现对目标场景地形高度的参数估计。基于该文所提算法,分别通过点目标模拟和DEM半实物模拟对该算法进行有效性验证及高程参数估计精度验证,并通过实测数据验证该算法的实用性。Abstract: Airborne Synthetic Aperture Radar Altimeter (SARA) is capable of exploiting the high-resolution in along-track, which has been attracted wide concerns. However, the existing re-tracking methods are mostly based on the least square operator. The performance of estimation accuracy and noise suppression of the operator are limited due to neglect of noise factors and accordance over-fitting problem. In this paper, Parameterized Retracking Bayes (PR-Bayes) algorithm is proposed under the framework of Bayesian machine learning. By introducing a prior probability model of the terrain scene, and combining with model-driven machine learning method, the elevation information of re-tracking with reliable estimation of the target can be achieved. The problem about over-fitting can be alleviated effectively. In this algorithm, Brown Model (BM) is used to recover complicated model parameters of SARA echo. Then, Hamilton Monte Carlo (HMC) statistical sampler is designed to estimate the terrain height of the scene with a high accuracy and reliable confidence. The accuracy and validity of this algorithm are verified by point target simulation and semi-physical simulation based on DEM respectively, and the practicability is proved by the airborne raw SARA data.
-
表 1 点目标仿真雷达参数
雷达参数 数值 雷达参数 数值 雷达参数 数值 雷达载频 9.6 GHz 采样频率 300 MHz 波长 3.13 cm 脉冲宽度 4 μs 天线孔径 0.4 m 飞行高度 1000 m 信号带宽 200 MHz 脉冲重复频率 2000 Hz 载机速度 60 m/s 表 2 点目标仿真实验结果
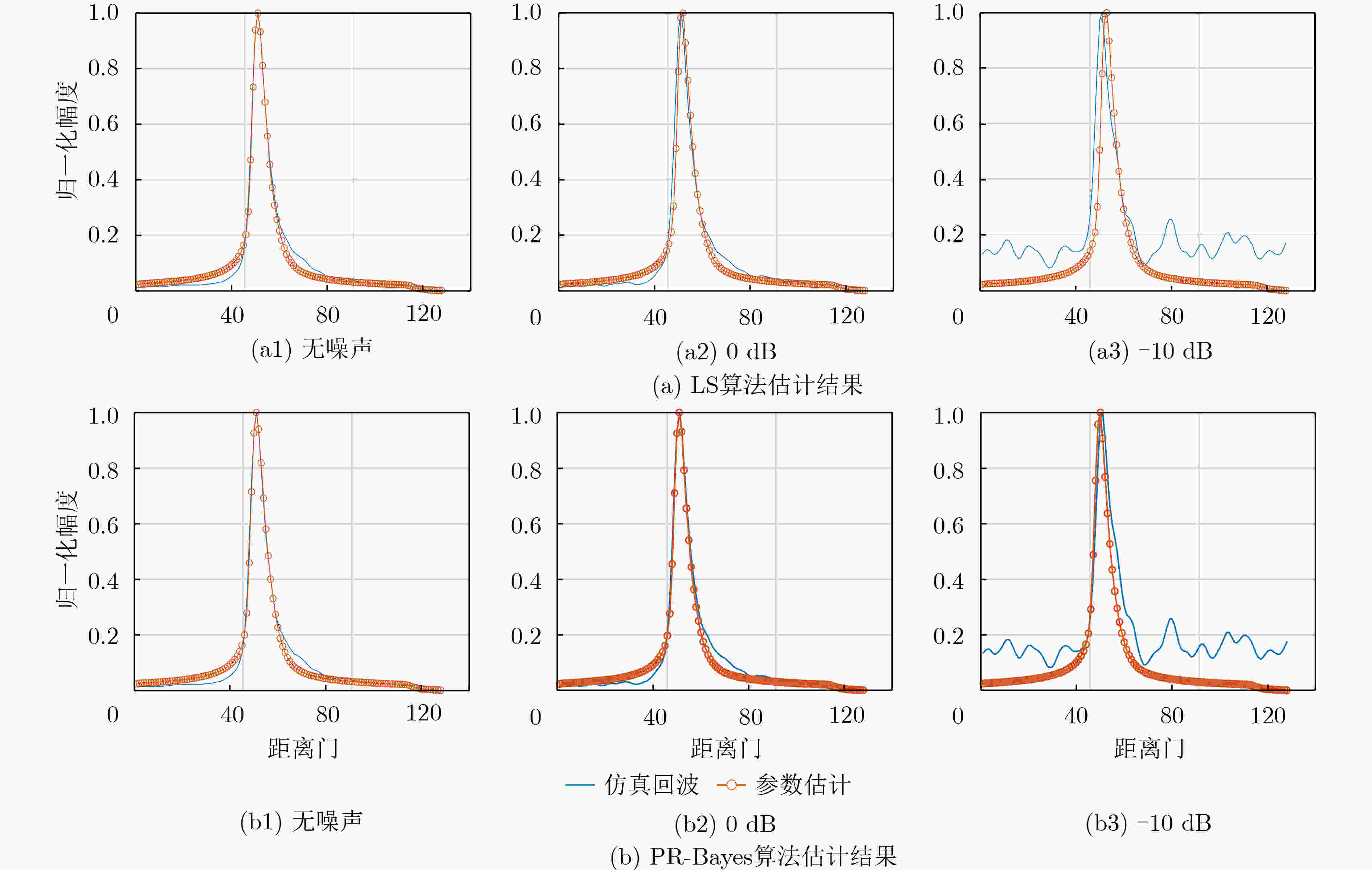
噪声(dB) 真值 LS估计值 PR-Bayes估计值 精度提升(%) 无噪声 50.40 50.04 50.04 0.55 0 50.40 51.02 50.08 50.25 -10 50.40 51.49 49.79 44.23 表 3 半实物仿真数据重跟踪结果定量分析
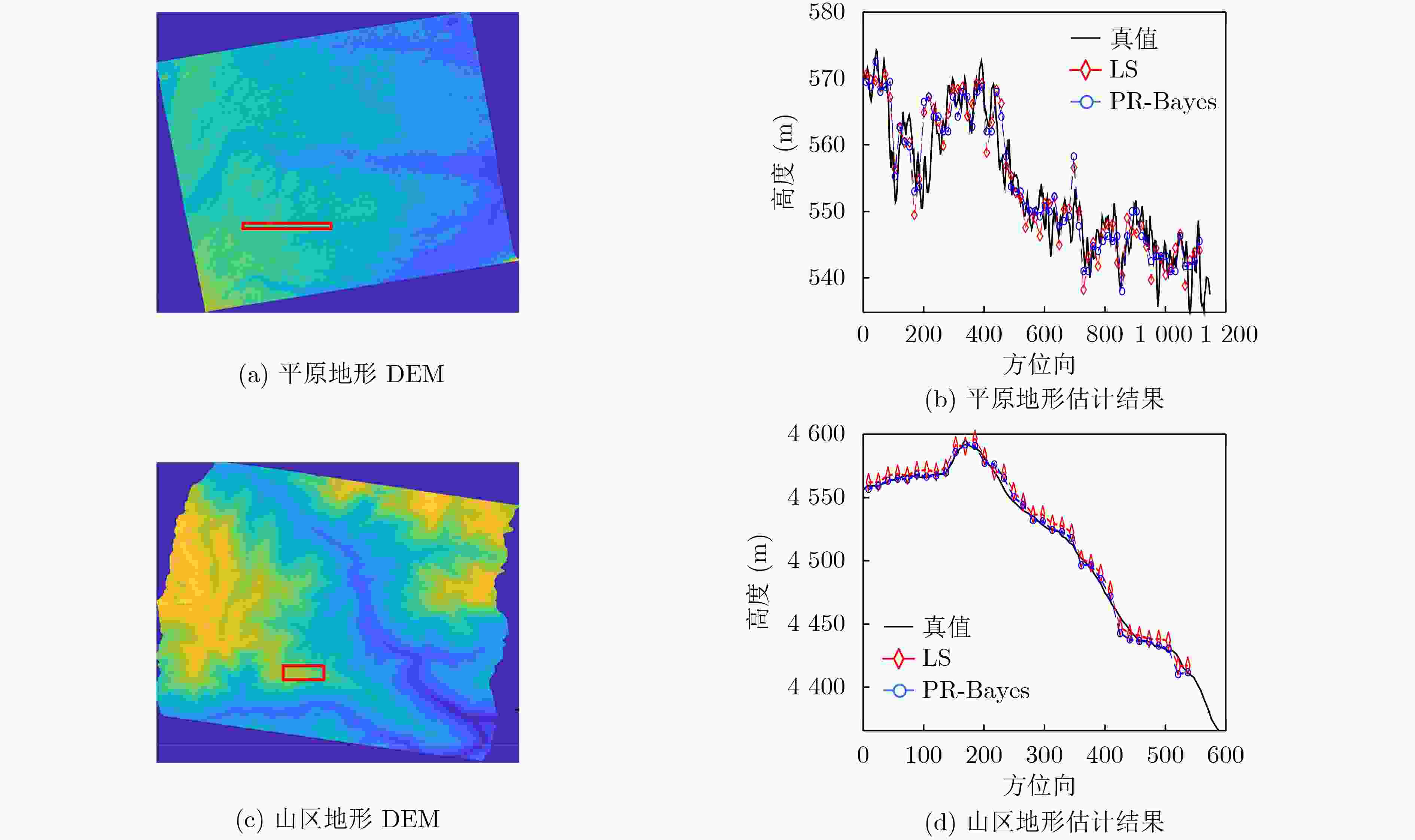
指标(m) LS PR-Bayes 平原STD 2.7852 2.0014 山区STD 1.7811 1.5231 表 4 机载实测数据参数
雷达参数 数值 雷达参数 数值 雷达参数 数值 雷达载频 9.6 GHz 采样频率 125 MHz 波长 3.13 cm 脉冲宽度 5 μs 天线孔径 0.4 m 飞行高度 2600 m 信号带宽 100 MHz 脉冲重复频率 2000 Hz 载机速度 60 m/s 表 5 实测数据重跟踪结果定量分析
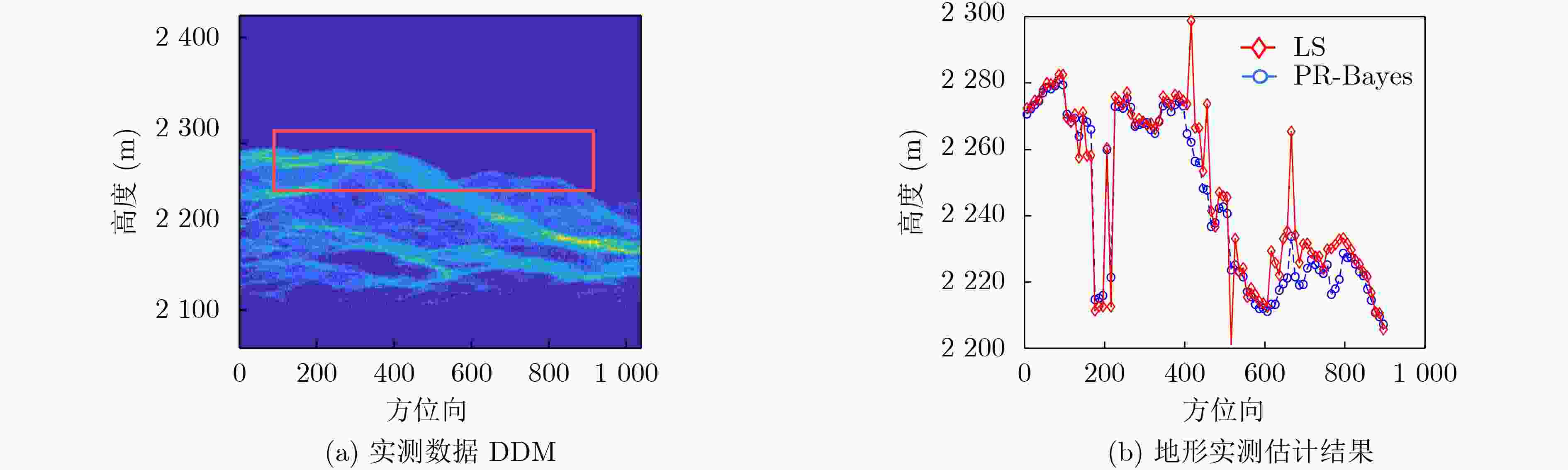
指标(m) LS PR-Bayes STD 14.74 12.22 -
[1] 刘鹏, 许可, 王磊, 等. 合成孔径雷达高度计与传统高度计精度比对分析与机载试验验证[J]. 电子与信息学报, 2016, 38(10): 2495–2501. doi: 10.11999/JEIT151354LIU Peng, XU Ke, WANG Lei, et al. Precision comparison and airborne experiment validation between SAR altimeter and conventional altimeter[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2495–2501. doi: 10.11999/JEIT151354 [2] QUILFEN Y and CHAPRON B. On denoising satellite altimeter measurements for high-resolution geophysical signal analysis[J]. Advances in Space Research, 2021, 68(2): 875–891. doi: 10.1016/j.asr.2020.01.005 [3] SHI Lingwei, XU Ke, LIU Peng, et al. Height precision of SAR altimeter and conventional radar altimeter based on flight experimental data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(6): 2676–2686. doi: 10.1109/JSTARS.2016.2550030 [4] 杨双宝, 翟振和, 许可, 等. 合成孔径雷达高度计数据处理方法[J]. 遥感技术与应用, 2017, 32(6): 1083–1092. doi: 10.11873/j.issn.1004-0323.2017.6.1083YANG Shuangbao, ZHAI Zhenhe, XU Ke, et al. The ground process segment of SAR altimeter[J]. Remote Sensing Technology and Application, 2017, 32(6): 1083–1092. doi: 10.11873/j.issn.1004-0323.2017.6.1083 [5] HALIMI A, MAILHES C, TOURNERET J Y, et al. A semi-analytical model for delay/Doppler altimetry and its estimation algorithm[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4248–4258. doi: 10.1109/TGRS.2013.2280595 [6] NEMETH C and FEARNHEAD P. Stochastic gradient Markov chain Monte Carlo[J]. Journal of the American Statistical Association, 2021, 116(533): 433–450. doi: 10.1080/01621459.2020.1847120 [7] CHAARI L, TOURNERET J Y, CHAUX C, et al. A Hamiltonian Monte Carlo method for non-smooth energy sampling[J]. IEEE Transactions on Signal Processing, 2016, 64(21): 5585–5594. doi: 10.1109/TSP.2016.2585120 [8] VAJARGAH K F, BENIS S G, and GOLSHAN H M. Detection of the quality of vital signals by the Monte Carlo Markov Chain (MCMC) method and noise deleting[J]. Health Information Science and Systems, 2021, 9(1): 26. doi: 10.1007/s13755-021-00157-5 [9] BRESSON G, CHATURVEDI A, RAHMAN M A, et al. Seemingly unrelated regression with measurement error: Estimation via Markov Chain Monte Carlo and mean field variational Bayes approximation[J]. The International Journal of Biostatistics, 2021, 17(1): 75–97. doi: 10.1515/ijb-2019-0120 [10] BAISTHAKUR S and CHAKRABORTY A. Experimental verification for load rating of steel truss bridge using an improved Hamiltonian Monte Carlo-based Bayesian model updating[J]. Journal of Civil Structural Health Monitoring, 2021, 11(4): 1093–1112. doi: 10.1007/s13349-021-00495-8 [11] BROWN G. The average impulse response of a rough surface and its applications[J]. IEEE Transactions on Antennas and Propagation, 1977, 25(1): 67–74. doi: 10.1109/TAP.1977.1141536 [12] BROWN G S. A useful approximation for the flat surface impulse response[J]. IEEE Transactions on Antennas and Propagation, 1989, 37(6): 764–767. doi: 10.1109/8.29363 [13] 何华锋, 戴嘉琪, 贺友. 弹载雷达导引头测高回波模型仿真研究[J]. 电光与控制, 2018, 25(11): 11–14,29. doi: 10.3969/j.issn.1671-637X.2018.11.002HE Huafeng, DAI Jiaqi, and HE You. Simulation of altimeter echo model for missile-borne radar seeker[J]. Electronics Optics &Control, 2018, 25(11): 11–14,29. doi: 10.3969/j.issn.1671-637X.2018.11.002 [14] EGIDO A and SMITH W H F. Fully focused SAR altimetry: Theory and applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 392–406. doi: 10.1109/TGRS.2016.2607122 [15] WARNER B D. Radar terrain return from the spherical earth at near vertical incidence[R]. AD260172, 1961. [16] 杨磊, 夏亚波, 毛欣瑶, 等. 基于分层贝叶斯Lasso的稀疏ISAR成像算法[J]. 电子与信息学报, 2021, 43(3): 623–631. doi: 10.11999/JEIT200292YANG Lei, XIA Yabo, MAO Xinyao, et al. Sparse ISAR imaging algorithm based on Bayesian-lasso[J]. Journal of Electronics &Information Technology, 2021, 43(3): 623–631. doi: 10.11999/JEIT200292 [17] YANG Lei, ZHAO Lifan, BI Guoan, et al. SAR ground moving target imaging algorithm based on parametric and dynamic sparse Bayesian learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(4): 2254–2267. doi: 10.1109/TGRS.2015.2498158 [18] 杨磊, 李埔丞, 李慧娟, 等. 稳健高效通用SAR图像稀疏特征增强算法[J]. 电子与信息学报, 2019, 41(12): 2826–2835. doi: 10.11999/JEIT190173YANG Lei, LI Pucheng, LI Huijuan, et al. Robust and efficient sparse-feature enhancement for generalized SAR imagery[J]. Journal of Electronics &Information Technology, 2019, 41(12): 2826–2835. doi: 10.11999/JEIT190173 [19] PROTIN F, JULES M, NGUYEN D T, et al. Unified modelling of epidemics by coupled dynamics via Monte-Carlo Markov Chain algorithms[J]. arXiv: 2106.13463, 2021. [20] YAO Yu and STEPHAN K E. Markov chain Monte Carlo methods for hierarchical clustering of dynamic causal models[J]. Human Brain Mapping, 2021, 42(10): 2973–2989. doi: 10.1002/hbm.25431 [21] HALIMI A, MAILHES C, TOURNERET J Y, et al. Bayesian estimation of smooth altimetric parameters: Application to conventional and delay/Doppler altimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(4): 2207–2219. doi: 10.1109/TGRS.2015.2497583 -






 下载:
下载:


 下载:
下载:
