Semi-supervised Bearing Fault Diagnosis Using Improved Graph Attention Network under Time-varying Speeds
-
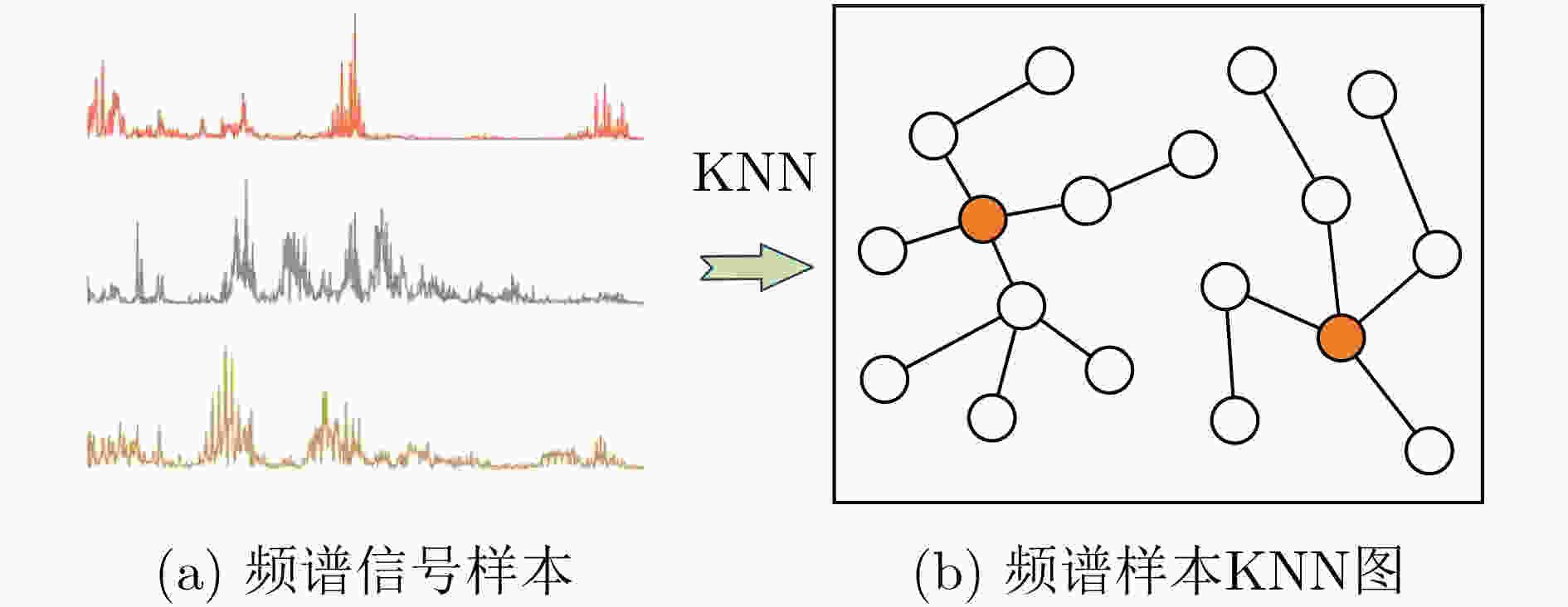
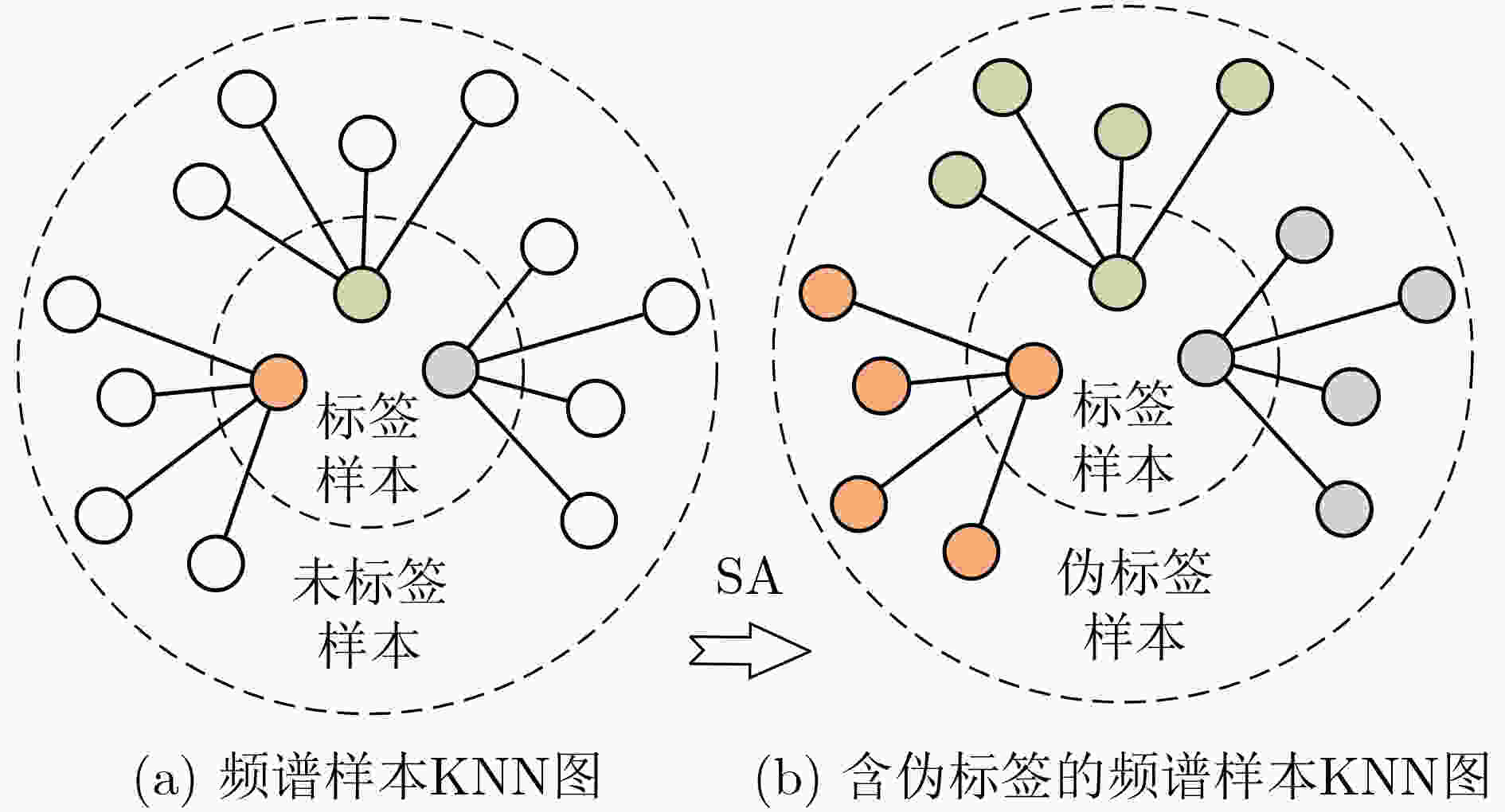
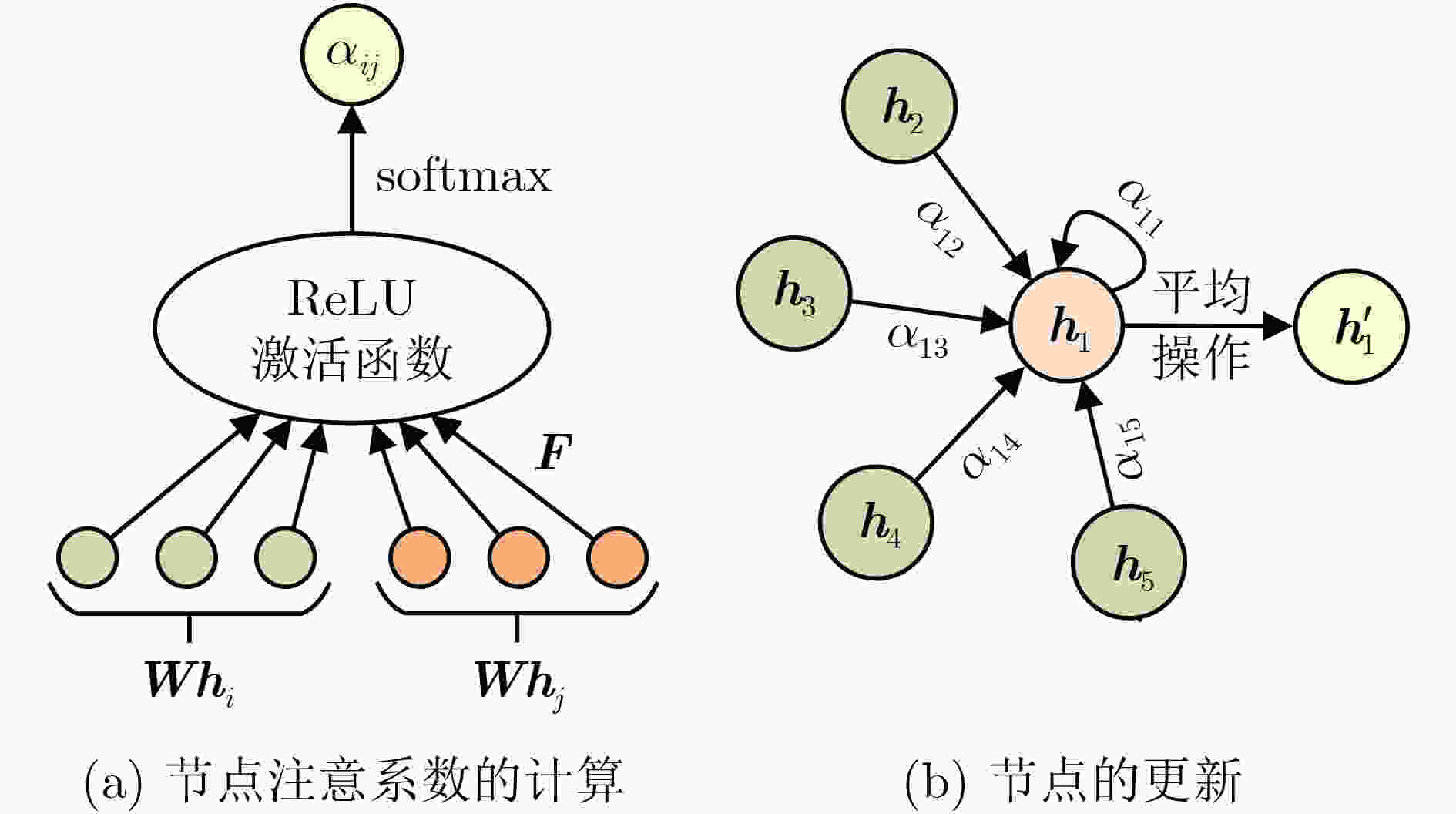
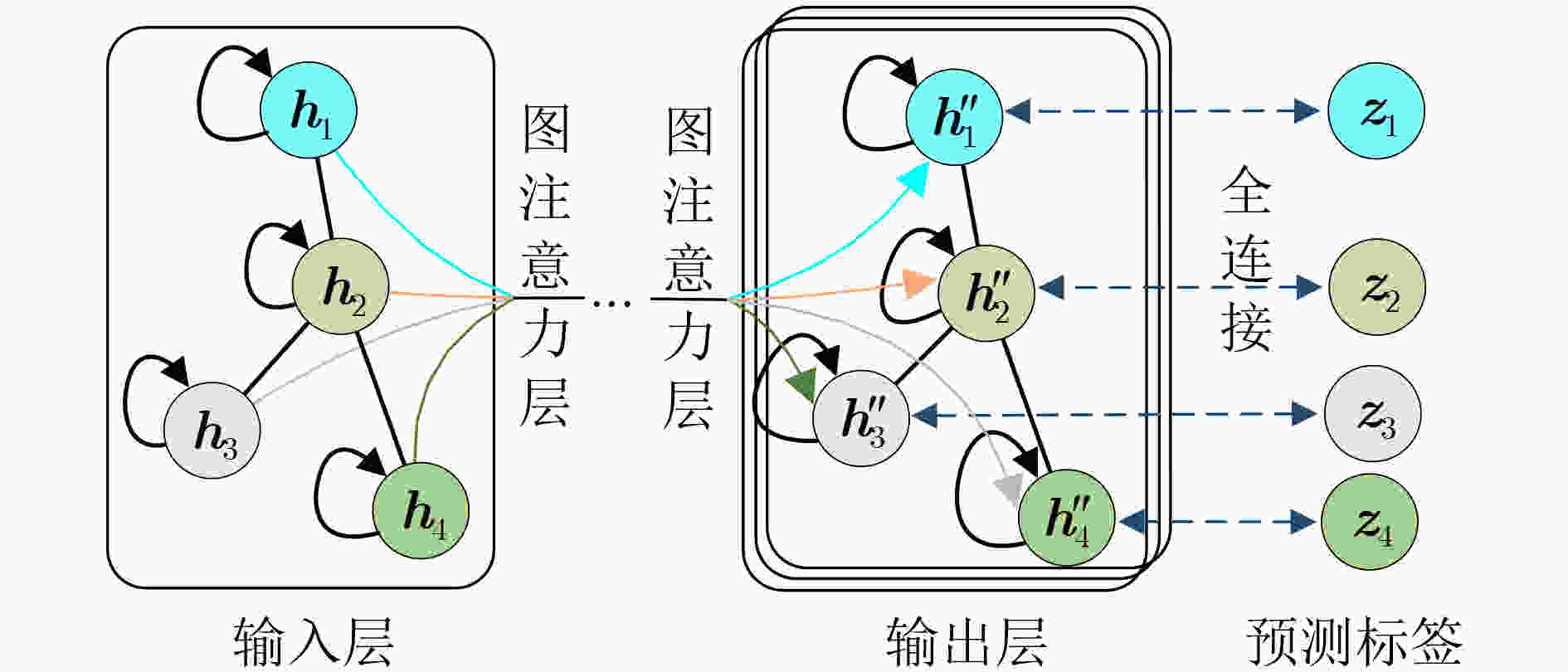
摘要: 新近的基于图神经网络(GNN)的轴承半监督故障诊断研究仍存在标签信息挖掘不充分和诊断场景较理想等问题。工程实际中,轴承经常运行于启停等时变转速工况,且故障标签样本的获取成本越发昂贵。针对以上挑战,该文提出时变转速下基于改进图注意力网络(GAT)的轴承半监督故障诊断新方法。基于K最近邻(KNN)算法和平滑假设(SA)设计伪标签传播策略,将标签信息沿边传播给分布相似的邻域样本,从而充分利用有限样本的标签信息。将每个振动频谱样本视为一个节点,构建基于节点级图注意力网络的半监督学习模型,通过注意力机制进一步挖掘代表性的轴承故障特征。将所提方法用于分析两组时变转速下轴承故障实验数据,结果表明所提方法能够在不超过2%的低标签率情况下,准确诊断轴承的不同故障模式,性能优于其他常用的图神经网络半监督学习方法。Abstract: Recent researches on semi-supervised bearing fault diagnosis based on Graph Neural Network (GNN) still have some problems, such as insufficient label information mining and relatively ideal diagnosis scenarios. In engineering practice, bearings are often operated under time-varying speeds such as startup and shutdown, and fault label samples become increasingly expensive. In response to the above challenges, a new method called semi-supervised bearing fault diagnosis using improved Graph ATtention network (GAT) under time-varying speeds is proposed. Based on K-Nearest Neighbor (KNN) algorithm and Smoothing Assumption (SA), the pseudo-label propagation strategy is designed to spread the label information to the neighborhood samples with similar distribution along the edge, so that the label information hidden in the limited samples can be fully utilized. Each vibration spectrum sample is considered as a node, and a semi-supervised learning model based on node-level GAN is constructed to explore further representative bearing fault features through the attention mechanism. The proposed method is applied to analyze two sets of bearing fault experimental data under time-varying speed, and the results show that the proposed method is able to diagnose accurately different fault modes of bearings at low label rates of no more than 2%, which is better than other commonly used semi-supervised learning methods of GNN.
-
算法1 所提方法的算法流程 输入:含伪标签的训练集(训练输入),无标签的测试集(测试输入) (1)设定k值、图注意力层层数、激活函数、学习率、迭代次数
T等模型超参数(2)随机初始化模型的权重等参数 (3)基于式(3)求解$ {L_{ij}} $,基于式(4)构造边,得到频谱样本KNN图 (4)基于式(5)得到标签样本集Y (5)For epoch in range(T): (6) 基于式(8)、式(9)得到输出节点集合Z (7) 基于式(10)计算损失函数Loss (8) 根据损失函数Loss基于Adam优化器更新模型参数 (9)End For (10)将训练好的模型用于测试集的预测 输出:测试集预测标签的准确率 表 1 轴承数据集信息
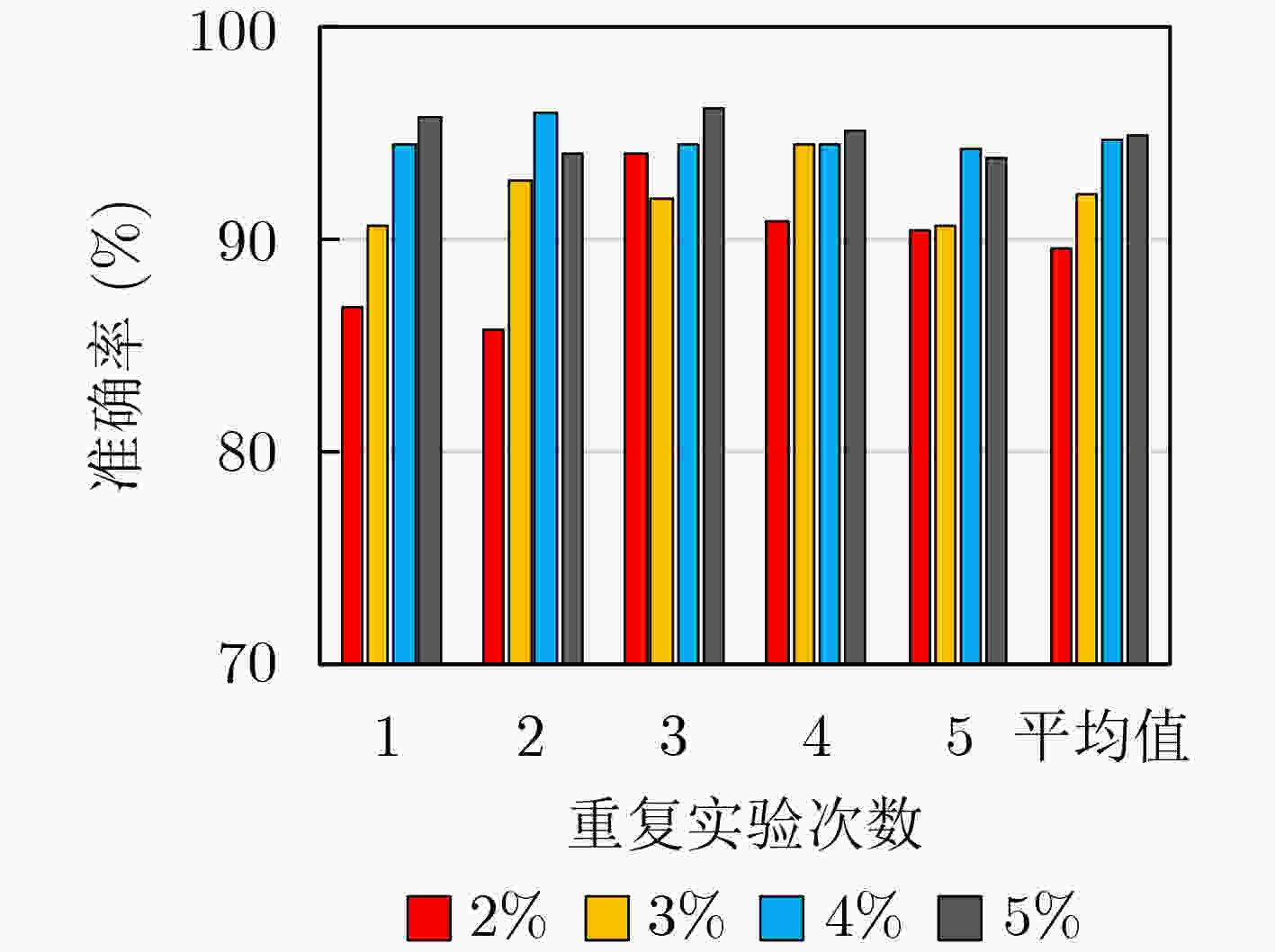
故障诊断案例 时变转速(r/min) 轴承状态 样本总数 标签样本数 训练样本数 案例1 0-3 000-0 正常 2 100(300×7) 42(6×7)(标签率2%) 350(50×7) 内圈轻度故障 内圈中度故障 内圈重度故障 外圈轻度故障 外圈中度故障 外圈重度故障 案例2 882-1 518-1 260 正常 1 000(200×5) 5(1×5)(标签率0.5%) 50(10×5) 906-1 464-1 122 内圈故障 865-1 421-928 滚珠故障 840-1 302-870 外圈故障 795-1 280-766 复合故障 表 2 各方法的诊断结果和运行时间
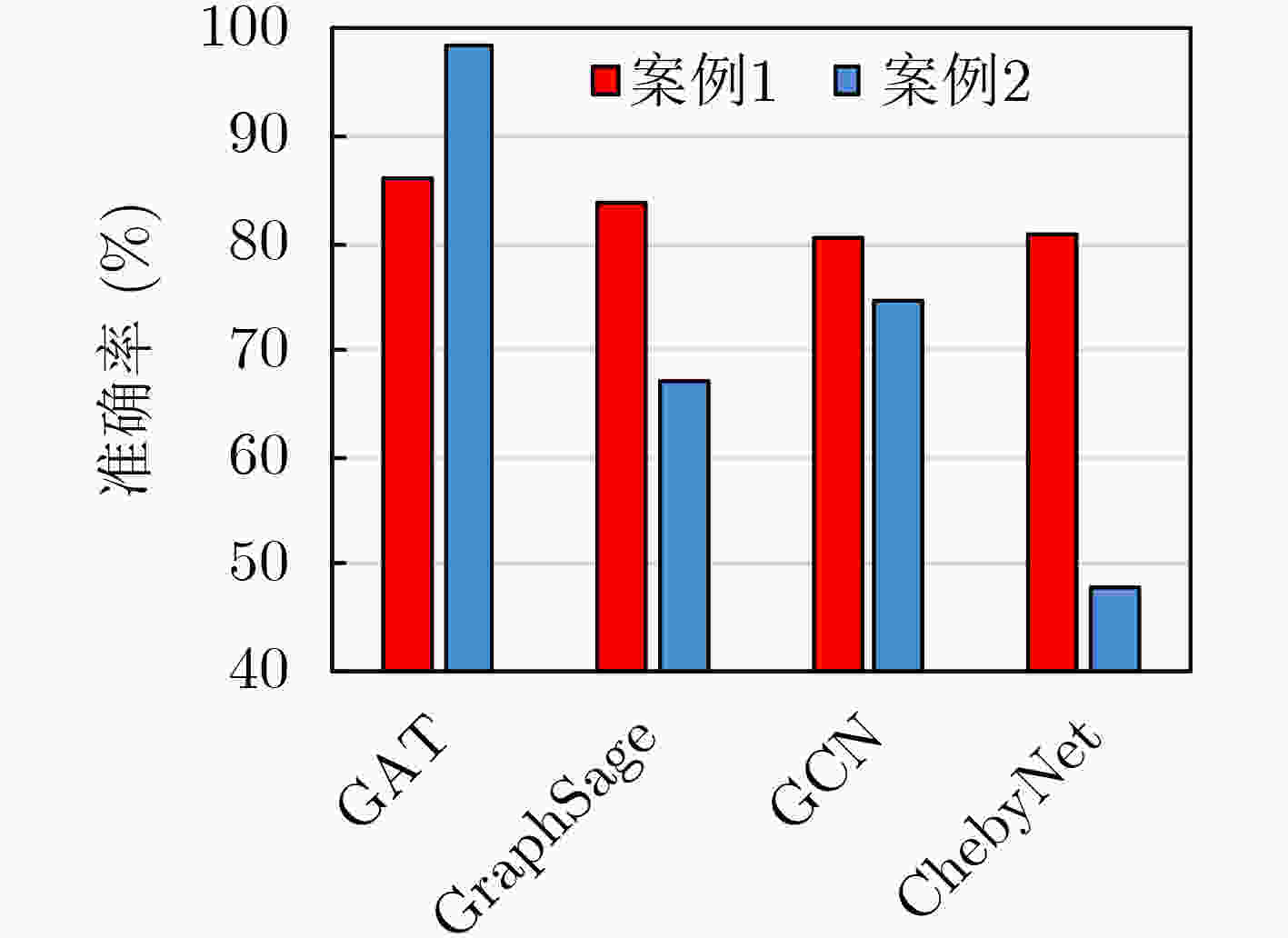
半监督故障诊断方法 准确率和方差 (%) 训练时间 (s) 测试时间 (s) 案例1 案例2 案例1 案例2 案例1 案例2 改进图注意力网络(KNN-SA-GAT) 89.62±3.36 99.58±0.45 5.39 6.20 0.01 0.01 GAT 86.07±4.42 98.55±0.81 5.39 6.21 0.01 0.01 KNN-SA-GraphSage 84.92±0.87 82.38±2.22 4.49 6.64 0.01 0.03 GraphSage 83.82±2.61 67.01±12.44 4.49 6.63 0.01 0.03 KNN-SA-GCN 84.53±2.59 84.99±4.44 4.59 5.24 0.01 0.01 GCN 80.63±5.11 74.55±7.58 4.55 5.23 0.01 0.01 KNN-SA-ChebyNet 86.25±5.58 79.85±4.39 5.40 7.44 0.02 0.05 ChebyNet 80.79±2.17 47.85±10.48 5.39 7.45 0.02 0.05 -
[1] 雷亚国, 贾峰, 孔德同, 等. 大数据下机械智能故障诊断的机遇与挑战[J]. 机械工程学报, 2018, 54(5): 94–104. doi: 10.3901/JME.2018.05.094LEI Yaguo, JIA Feng, KONG Detong, et al. Opportunities and challenges of machinery intelligent fault diagnosis in big data era[J]. Journal of Mechanical Engineering, 2018, 54(5): 94–104. doi: 10.3901/JME.2018.05.094 [2] 邵海东, 张笑阳, 程军圣, 等. 基于提升深度迁移自动编码器的轴承智能故障诊断[J]. 机械工程学报, 2020, 56(9): 84–90. doi: 10.3901/JME.2020.09.084SHAO Haidong, ZHANG Xiaoyang, CHENG Junsheng, et al. Intelligent fault diagnosis of bearing using enhanced deep transfer auto-encoder[J]. Journal of Mechanical Engineering, 2020, 56(9): 84–90. doi: 10.3901/JME.2020.09.084 [3] 文成林, 吕菲亚. 基于深度学习的故障诊断方法综述[J]. 电子与信息学报, 2020, 42(1): 234–248. doi: 10.11999/JEIT190715WEN Chenglin and LV Feiya. Review on deep learning based fault diagnosis[J]. Journal of Electronics &Information Technology, 2020, 42(1): 234–248. doi: 10.11999/JEIT190715 [4] LIANG Pengfei, DENG Chao, WU Jun, et al. Intelligent fault diagnosis via semisupervised generative adversarial nets and wavelet transform[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(7): 4659–4671. doi: 10.1109/tim.2019.2956613 [5] RAZAVI-FAR R, HALLAJI E, FARAJZADEH-ZANJANI M, et al. A semi-supervised diagnostic framework based on the surface estimation of faulty distributions[J]. IEEE Transactions on Industrial Informatics, 2019, 15(3): 1277–1286. doi: 10.1109/tii.2018.2851961 [6] YU Kun, MA Hui, LIN Tianran, et al. A consistency regularization based semi-supervised learning approach for intelligent fault diagnosis of rolling bearing[J]. Measurement, 2020, 165: 107987. doi: 10.1016/j.measurement.2020.107987 [7] TAO Xinmin, REN Chao, LI Qing, et al. Bearing defect diagnosis based on semi-supervised kernel Local Fisher discriminant analysis using pseudo labels[J]. ISA Transactions, 2021, 110: 394–412. doi: 10.1016/j.isatra.2020.10.033 [8] WU Xinya, ZHANG Yan, CHENG Changming, et al. A hybrid classification autoencoder for semi-supervised fault diagnosis in rotating machinery[J]. Mechanical Systems and Signal Processing, 2021, 149: 107327. doi: 10.1016/j.ymssp.2020.107327 [9] NIE Xiaoyin and XIE Gang. A two-stage semi-supervised learning framework for fault diagnosis of rotating machinery[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 3521212. doi: 10.1109/tim.2021.3091489 [10] WU Zonghan, PAN Shirui, CHEN Fengwen, et al. A comprehensive survey on graph neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4–24. doi: 10.1109/TNNLS.2020.2978386 [11] ZHAO Xiaoli, JIA Minping, and LIU Zheng. Semisupervised graph convolution deep belief network for fault diagnosis of electormechanical system with limited labeled data[J]. IEEE Transactions on Industrial Informatics, 2021, 17(8): 5450–5460. doi: 10.1109/tii.2020.3034189 [12] GAO Yiyuan, CHEN Mang, and YU Dejie. Semi-supervised graph convolutional network and its application in intelligent fault diagnosis of rotating machinery[J]. Measurement, 2021, 186: 110084. doi: 10.1016/j.measurement.2021.110084 [13] TANG Yao, ZHANG Xiaofei, ZHAI Yujia, et al. Rotating machine systems fault diagnosis using semisupervised conditional random field-based graph attention network[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 3521010. doi: 10.1109/tim.2021.3091212 [14] 向敏, 饶华阳, 张进进, 等. 基于图卷积神经网络的软件定义电力通信网络路由控制策略[J]. 电子与信息学报, 2021, 43(2): 388–395. doi: 10.11999/JEIT190971XIANG Min, RAO Huayang, ZHANG Jinjin, et al. Software-defined power communication network routing control strategy based on graph convolution network[J]. Journal of Electronics &Information Technology, 2021, 43(2): 388–395. doi: 10.11999/JEIT190971 [15] 盛晓光, 王颖, 钱力, 等. 基于图卷积半监督学习的论文作者同名消歧方法研究[J]. 电子与信息学报, 2021, 43(12): 3442–3450. doi: 10.11999/JEIT200905SHENG Xiaoguang, WANG Ying, QIAN Li, et al. Author name disambiguation based on semi-supervised learning with graph convolutional network[J]. Journal of Electronics &Information Technology, 2021, 43(12): 3442–3450. doi: 10.11999/JEIT200905 [16] CHEN Ke and WANG Shihai. Semi-supervised learning via regularized boosting working on multiple semi-supervised assumptions[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(1): 129–143. doi: 10.1109/TPAMI.2010.92 [17] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks[EB/OL]. https://arxiv.org/abs/1710.10903, 2018. [18] LI Tianfu, ZHOU Zheng, LI Sinan, et al. The emerging graph neural networks for intelligent fault diagnostics and prognostics: A guideline and a benchmark study[J]. Mechanical Systems and Signal Processing, 2022, 168: 108653. doi: 10.1016/j.ymssp.2021.108653 [19] WANG Jinrui, LI Shunming, HAN Baokun, et al. Construction of a batch-normalized autoencoder network and its application in mechanical intelligent fault diagnosis[J]. Measurement Science and Technology, 2019, 30(1): 015106. doi: 10.1088/1361-6501/aaf319 [20] LIU Shen, CHEN Jinglong, HE Shuilong, et al. Subspace network with shared representation learning for intelligent fault diagnosis of machine under speed transient conditions with few samples[J]. ISA Transactions, 2022, 128: 531–544. [21] SHI Zhen, CHEN Jinglong, ZI Yanyang, et al. A novel multitask adversarial network via redundant lifting for multicomponent intelligent fault detection under sharp speed variation[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 3511010. doi: 10.1109/tim.2021.3055821 [22] HUANG Huan and BADDOUR N. Bearing vibration data collected under time-varying rotational speed conditions[J]. Data in Brief, 2018, 21: 1745–1749. doi: 10.1016/j.dib.2018.11.019 [23] HAMILTON W L, YING R, and LESKOVEC J. Inductive representation learning on large graphs[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 1025–1035. [24] DEFFERRARD M, BRESSON X, and VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering[C]. The 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 2016: 3844–3852. [25] KIPF T N and WELLING M. Semi-supervised classification with graph convolutional networks[C]. The 5th International Conference on Learning Representations, Toulon, France, 2017. -






 下载:
下载:




 下载:
下载:
