Outage Performance Analysis and Power Allocation Algorithm of Multi-user Cognitive Radio Non-Orthogonal Multiple Access System
-
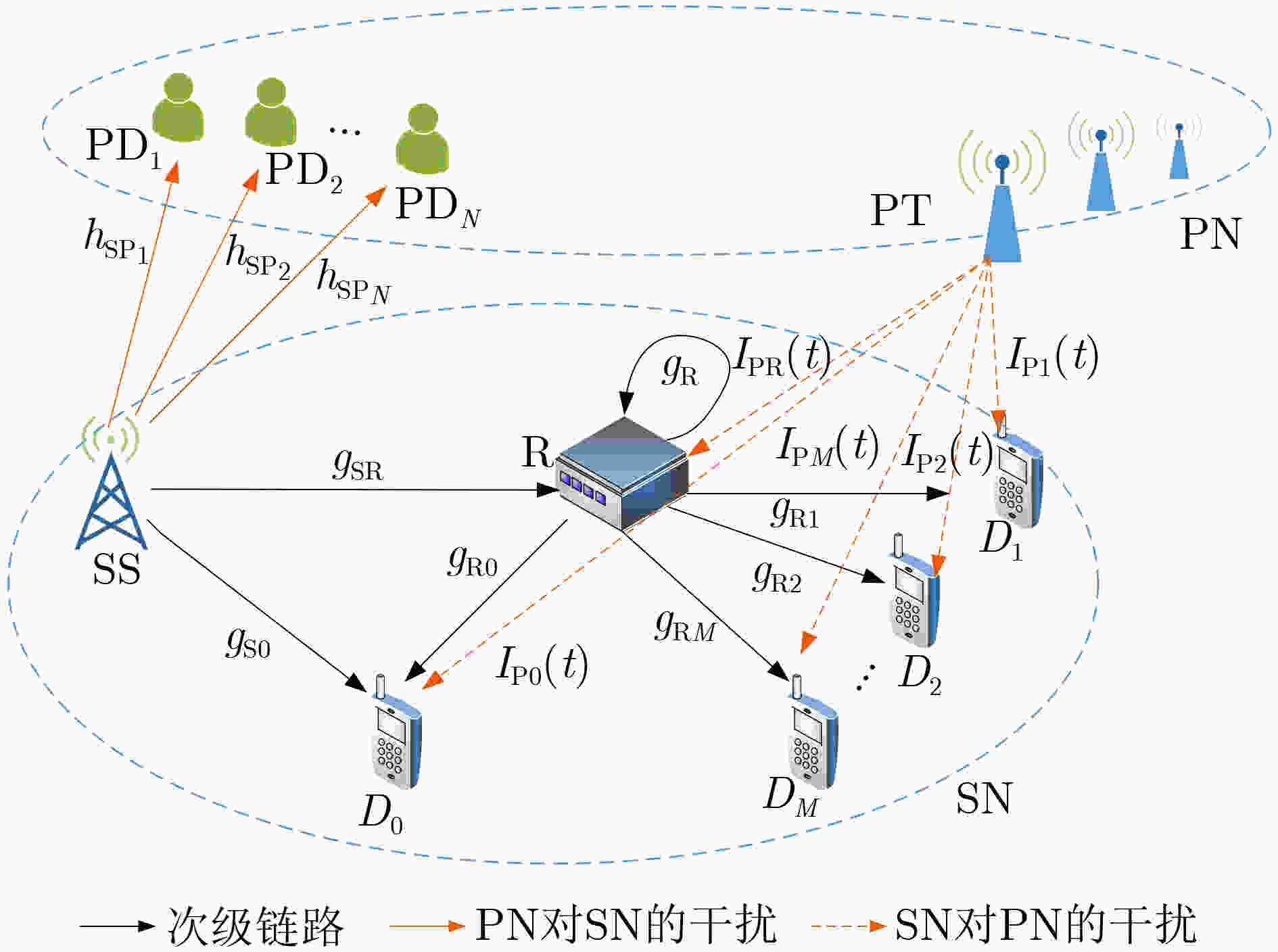
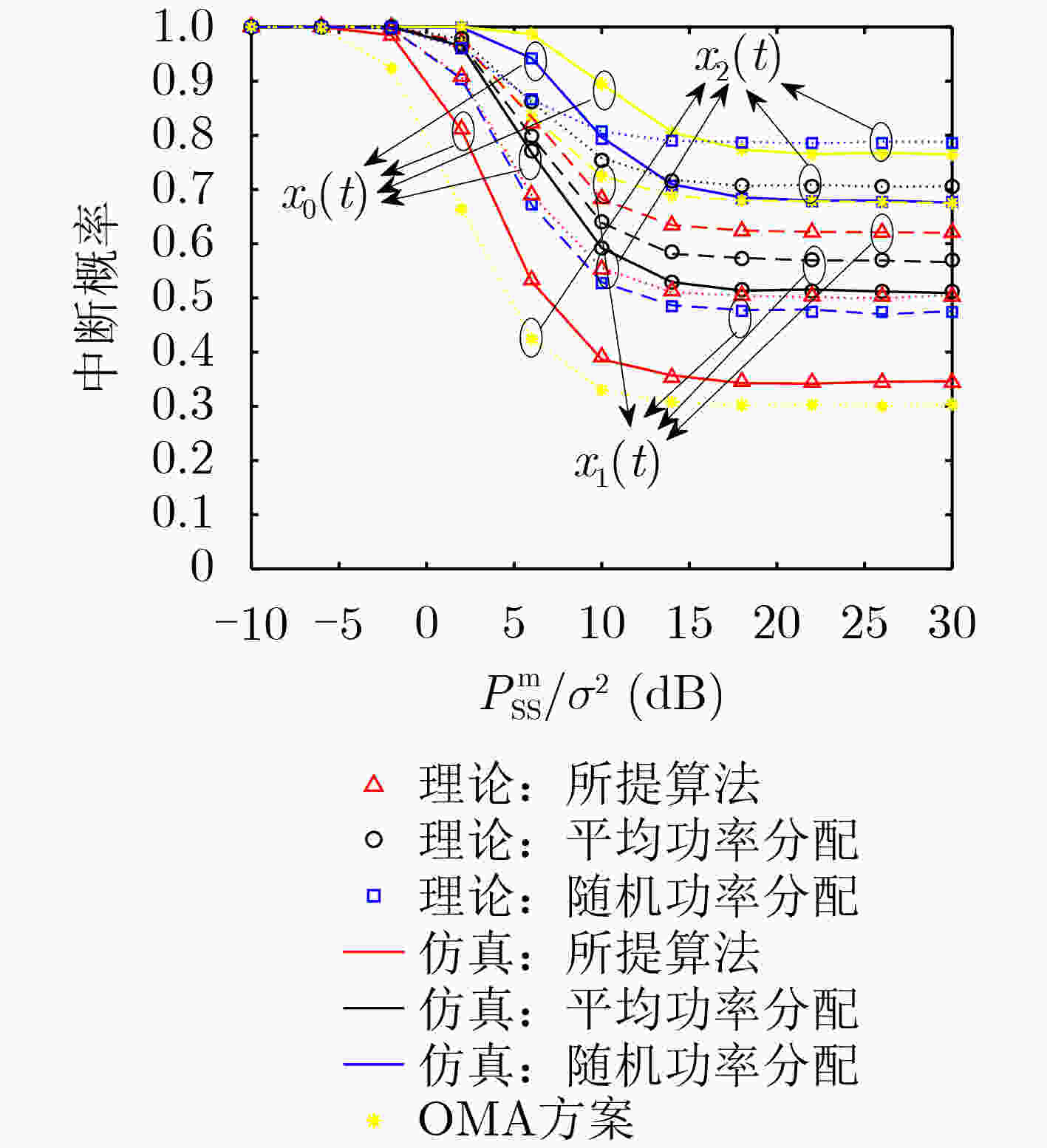
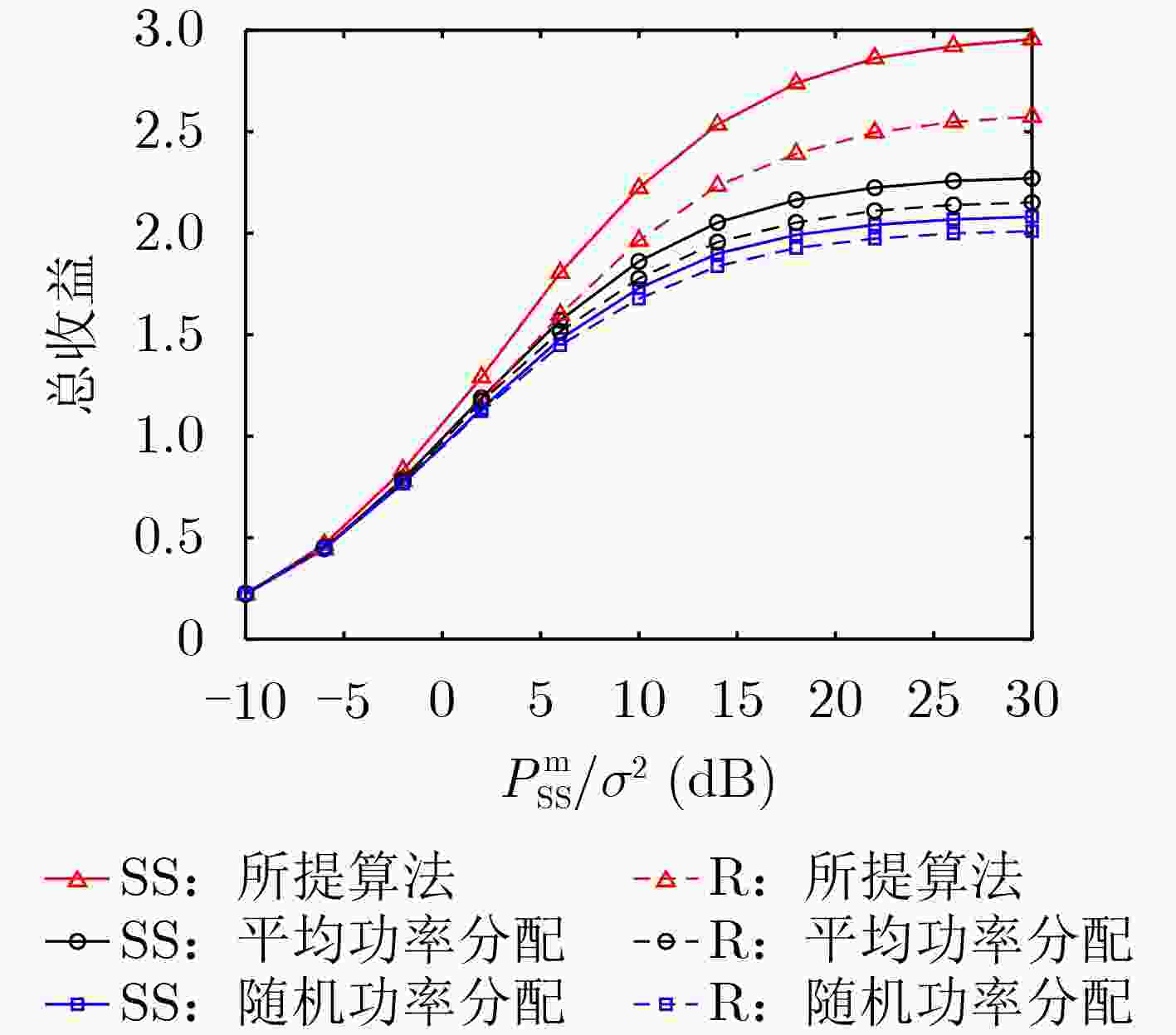
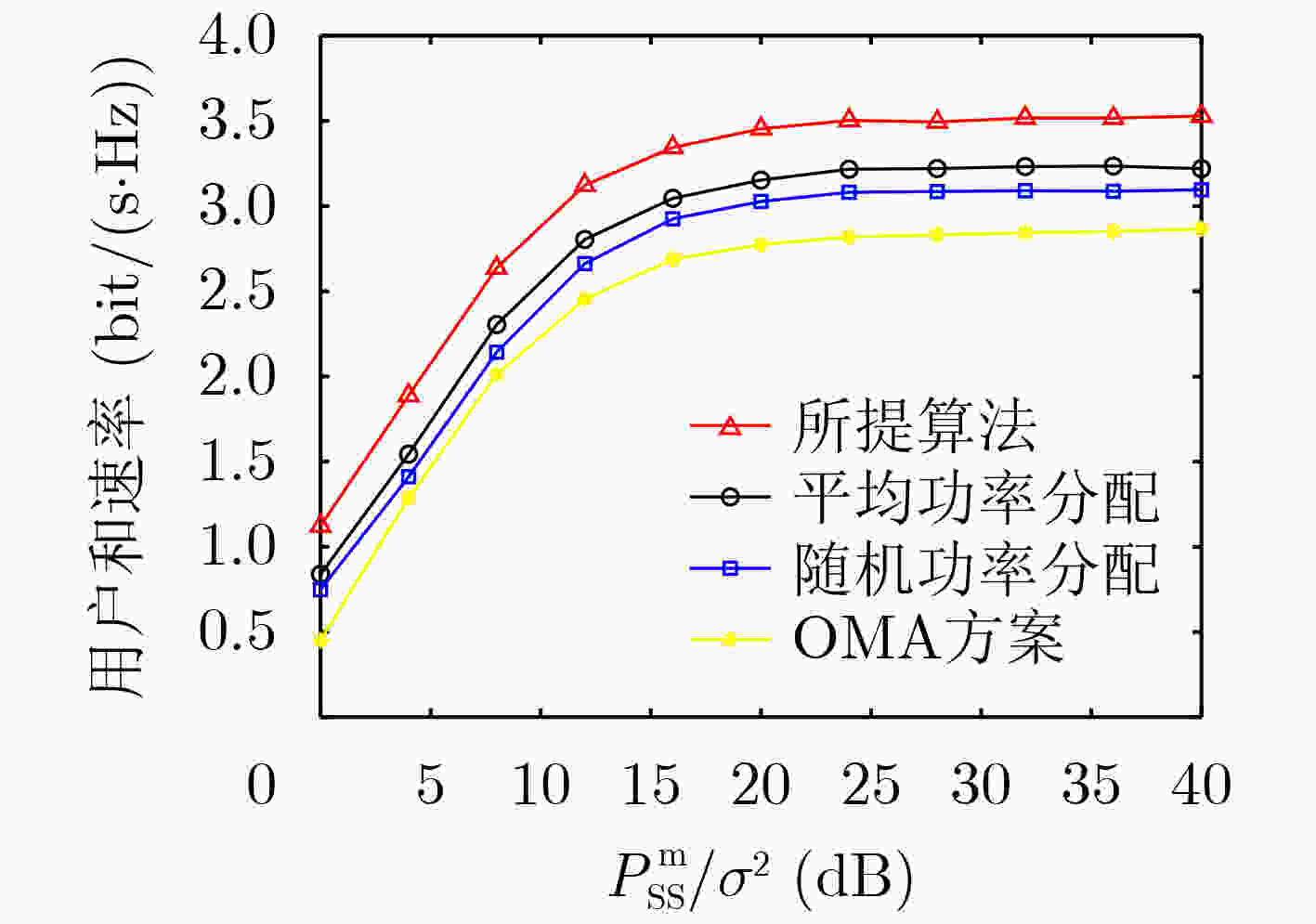
摘要: 非正交多址接入(NOMA)是5G网络关键候选技术之一,其与认知无线电(CR)技术相结合形成系统(CR-NOMA),能够实现更高的频谱效率及更大的吞吐量。该文将直传与中继协同传输(CDRT)方案引入多用户CR-NOMA系统,其中CDRT表示次级源(SS)直接与近端次级用户通信,而仅通过中继(R)与多个远端次级用户通信。在非理想自干扰消除和全双工(FD)中继情况下,推导了每个NOMA用户中断概率(OP)的精确闭式表达。此外,在该系统模型下分析SS, R和用户的收益最优化问题,提出一种基于收益的两阶段迭代功率分配算法。仿真结果显示,在高信噪比(30 dB)条件下,与随机功率分配及平均功率分配方案相比,该文所提算法的用户和速率、SS总收益、R总收益分别可最高提升13%, 56%及26%。蒙特卡罗仿真验证了理论分析与实验结果的一致性。Abstract: Non-Orthogonal Multiple Access (NOMA) is one of the key candidate technologies for 5G networks. Combined with Cognitive Radio (CR) technology, the CR-NOMA system achieves higher spectral efficiency and greater throughput quantity. The Coordinated Direct and Relay Transmission (CDRT) technology is introduced into the CR-NOMA system in this paper, where one Secondary Source (SS) communicates directly with one near-end secondary user, and the SS can only communicate with multiple far-end secondary users with the help of one Relay (R) node. With imperfect self-interference cancellation and Full-Duplex (FD) relaying, closed-form expressions for the Outage Probability (OP) of the NOMA users are derived. In addition, the revenue optimization problem of SS, R, and the users is analyzed, and an iterative algorithm of two-step user power allocation is proposed. Simulation results show, under the condition of a high signal-to-noise ratio (30 dB), compared with the average power allocation scheme and the random power allocation scheme, the proposed algorithm increases the user sum rate by up to 13%, the SS total income by 56%, and the R total income by 26%. Monte Carlo simulations verify that the theoretical analysis well matches the experimental results.
-
表 1 公式符号表
公式符号 符号含义 ${h_{{\text{S}}{{\text{P}}_n}}}(1 \le n \le N)$ SS与PD之间的信道系数 $h_{{\text{SP}}}^{{\text{max}}}$ SS与PD之间的最优信道系数 $ {g_\varphi },\varphi \in \{ {\text{SR}},{\text{R}},{\text{R0}},{\text{R}}m\} (1 \le m \le M) $ 次级节点之间的信道系数 ${I_{ {\text{PS} } } }{\text{~} }{\rm{CN}}(0,\tau {\sigma ^2})$ PN对SN的干扰 $\tau $ PN对SN的干扰因子 ${T_{{\text{ITC}}}}$ 干扰温度限制 $M$ 远端用户数量 ${\alpha _0},{\alpha _m}(1 \le m \le M)$ SS处用户功率分配因子 $ P_{{\text{SS}}}^{\text{m}} $ SS最大发射功率 ${\rho _{{\text{SS}}}}$ SS处对应的发射信噪比 ${\rho _{\text{R}}}$ R处对应的发射信噪比 ${\beta _m}(1 \le m \le M)$ R处用户功率分配因子 ${\hat f_{ {\text{R0} } } }{\text{~} }{\rm{CN}}(0,\xi \sigma _{ {\text{R0} } }^{\text{2} })$ ${D_{\text{0}}}$处残余干扰信道系数 ${\hat f_{\text{R} } }{\text{~} }{\rm{CN}}(0,\eta \sigma _{\text{R} }^{\text{2} })$ R处的残余自干扰信道系数 $\xi $ ${D_{\text{0}}}$处残余干扰因子 $\eta $ R处残余自干扰因子 ${u_0},{u_m}(1 \le m \le M)$ 用户可达速率门限转换信噪比 ${\mathcal{R}_0},{\mathcal{R}_m}(1 \le m \le M)$ ${D_{\text{0}}}$与R处信号实际可达速率 算法1 两阶段迭代功率分配算法 输入:${\varOmega _i},0 \le i \le M + 1$, $\alpha _0^*$, $\alpha _1^*$ 输出:${\text{P}}{{\text{A}}^*}$ (1)初始化$\alpha _0^* = \min (1,\alpha _0^*)$, $\alpha _1^* = \max (0,\alpha _1^*)$, $j = 1$ (2)${P^*} = {\text{zeros} }({\text{1} },{{M - 1} })$, ${\text{P}}{{\text{A}}^*} = [\alpha _0^*,\alpha _1^*,{P^*}]$ (3) ${\text{Whlie}}\;\;\;{\kern 1pt} j < M + 1$ (4) ${\text{If}}\;\;\;{\kern 1pt} \alpha _j^* = 0$ (5) ${P^*}(1,j) = {\alpha _j}$ (6) ${\text{ElseIf}}\;\;\;{\kern 1pt} \alpha _j^* > 0$且$j \leqslant M + 1$ (7) ${\alpha _{{\text{max}}}} = \alpha _j^*$ (8) 通过上述最优化问题求解,计算${\alpha _j}$的最优解$\alpha _j^*$ (9) $\alpha _j^* = \min (1,\alpha _j^*)$ (10) $\alpha _{j + 1}^* = \max (0,{\alpha _{{\text{max}}}} - \alpha _j^*)$ (11) ${P^*}(1,j) = \alpha _j^*$ (12) ${P^*}(1,j + 1) = \alpha _{j + 1}^*$ (13) $j = j + 1$ (14) ${\text{EndIf}}$ (15) ${\text{EndWhile}}$ 表 2 仿真参数设置
仿真参数 参数取值 $ {\alpha _0},{\alpha _1},{\alpha _2} $ 0.1,0.3,0.6 ${r_{\text{0}}} = {r_{\text{1}}} = {r_{\text{2}}}$ 1 bit/(s·Hz) ${\beta _{\text{1}}},{\beta _{\text{2}}}$ 0.4,0.6 ${P_{\text{SS} } }^{\rm{m}}/{\sigma ^{\text{2} } }$ –10~40 dB ${P_{\text{R}}}/{\sigma ^{\text{2}}}$ 10 dB $ {\text{|}}{g_\varphi }{{\text{|}}^{\text{2}}},|{h_{{\text{S}}{{\text{P}}_n}}}{|^2} $ 服从$\dfrac{1}{2}{ {\text{e} }^{ - \frac{1}{2}x} }$分布 $|{\hat f_{{\text{R0}}}}{|^2},|{\hat f_{\text{R}}}{|^2}$ 服从$\dfrac{1}{ {2 \times 0.001} }{ {\text{e} }^{ - \frac{1}{ {2\; \times \;0.001} }x} }$分布 $\tau $ 0.01 -
[1] BOCCARDI F, HEATH R W, LOZANO A, et al. Five disruptive technology directions for 5G[J]. IEEE Communications Magazine, 2014, 52(2): 74–80. doi: 10.1109/MCOM.2014.6736746 [2] TIMOTHEOU S and KRIKIDIS I. Fairness for non-orthogonal multiple access in 5G systems[J]. IEEE Signal Processing Letters, 2015, 22(10): 1647–1651. doi: 10.1109/LSP.2015.2417119 [3] 3GPP. Study on downlink multiuser superposition transmission (MUST) for LTE (Release 13)[R]. TR36.859, 2015. [4] BABU V S, DEEPAN N, and REBEKKA B. Performance analysis of cooperative full duplex NOMA system in cognitive radio networks[C]. 2020 International Conference on Wireless Communications Signal Processing and Networking (WiSPNET), Chennai, India, 2020: 84–87. [5] IM G and LEE J H. Outage probability for cooperative NOMA systems with imperfect SIC in cognitive radio networks[J]. IEEE Communications Letters, 2019, 23(4): 692–695. doi: 10.1109/LCOMM.2019.2903040 [6] ARZYKULOV S, TSIFTSIS T A, NAURYZBAYEV G, et al. Outage performance of cooperative underlay CR-NOMA with imperfect CSI[J]. IEEE Communications Letters, 2019, 23(1): 176–179. doi: 10.1109/LCOMM.2018.2878730 [7] SUN Fan, DE CARVALHO E, POPOVSKI P, et al. Coordinated direct and relay transmission with linear non-regenerative relay beamforming[J]. IEEE Signal Processing Letters, 2012, 19(10): 680–683. doi: 10.1109/LSP.2012.2211588 [8] KADER M F, SHIN S Y, and LEUNG V C M. Full-duplex non-orthogonal multiple access in cooperative relay sharing for 5G systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(7): 5831–5840. doi: 10.1109/TVT.2018.2799939 [9] KIM J B and LEE I H. Non-orthogonal multiple access in coordinated direct and relay transmission[J]. IEEE Communications Letters, 2015, 19(11): 2037–2040. doi: 10.1109/LCOMM.2015.2474856 [10] ZHONG Caijun and ZHANG Zhaoyang. Non-orthogonal multiple access with cooperative full-duplex relaying[J]. IEEE Communications Letters, 2016, 20(12): 2478–2481. doi: 10.1109/LCOMM.2016.2611500 [11] DONG Kunming, SHEN Bin, JIANG Huilin, et al. Outage performance analysis of underlay CR-NOMA network with coordinated direct and relay transmissions[C]. The 94th Vehicular Technology Conference (VTC2021-Fall), Norman, USA, 2021: 1–6. [12] PEI Xinyue, YU Hua, WEN Miaowen, et al. NOMA-based coordinated direct and relay transmission with a half-duplex/full-duplex relay[J]. IEEE Transactions on Communications, 2020, 68(11): 6750–6760. doi: 10.1109/TCOMM.2020.3017002 [13] VU T H, NGUYEN T V, DA COSTA D B, et al. Performance analysis and deep learning design of underlay cognitive NOMA-based CDRT networks with imperfect SIC and co-channel interference[J]. IEEE Transactions on Communications, 2021, 69(12): 8159–8174. doi: 10.1109/TCOMM.2021.3110209 [14] LEE I H and JUNG H. User selection and power allocation for downlink NOMA systems with quality-based feedback in Rayleigh fading channels[J]. IEEE Wireless Communications Letters, 2020, 9(11): 1924–1927. doi: 10.1109/LWC.2020.3008174 [15] 于宝泉, 蔡跃明, 胡健伟. 认知无线电非正交多址接入随机网络物理层安全性能分析[J]. 电子与信息学报, 2020, 42(4): 950–956. doi: 10.11999/JEIT190049YU Baoquan, CAI Yueming, and HU Jianwei. Performance analysis of physical layer security for cognitive radio non-orthogonal multiple access random network[J]. Journal of Electronics &Information Technology, 2020, 42(4): 950–956. doi: 10.11999/JEIT190049 [16] SHEN Zhou, LIU Gang, DING Zhiguo, et al. Optimal power allocations for 5G non-orthogonal multiple access with half/full duplex relaying[C]. 2019 IEEE International Conference on Communications (ICC), Shanghai, China, 2019: 1–7. -





 下载:
下载:


 下载:
下载:
