A Multiple Extended Target Generalized Labeled Multi-Bernoulli Filter Based on Joint Likelihood Function
-
摘要: 高分辨率雷达监视系统可观测到区域内不同形状的多个扩展目标,可靠的形状估计有利于提高扩展目标跟踪性能,并可作为战场态势评估的重要依据。该文针对不同形状多扩展目标跟踪问题,提出一种基于联合似然函数的广义标签多伯努利(JL-GLMB)滤波器,可实现目标数目、航迹以及形状的精确估计。首先,将目标形状建模为星凸集,并利用非线性量测变换滤波器更新GLMB分布中的高斯分量,有效提高扩展目标状态估计精度。然后,通过对数加权融合策略,构造联合似然函数,综合衡量扩展目标和量测单元之间的相似程度。最后,基于吉布斯采样,提出快速计算扩展目标状态后验概率密度的方法,有效提高数据关联的准确率和计算效率。仿真实验结果表明,所提滤波器能够有效估计不同形状的多扩展目标状态,且在杂波环境下具有稳定的势估计。Abstract: High-resolution radar systems monitor multiple extended targets with different shapes in a surveillance area. Reliable shapes estimation can effectively improve tracking performance and are crucial to battle-field situation evaluations. In this paper, a Joint Likelihood based Generalized Labeled Multi-Bernoulli (JL-GLMB) filter is proposed to estimate accurately the number of targets, target tracks, and target shapes. Firstly, the extended target is modeled as a star-convex set, and Gaussian components in the GLMB density are updated by the measurement transformation filter to improve the accuracy of state estimation. Then, a joint likelihood function is constructed by log-weighted fusion strategy to measure comprehensively the similarity between extended target and measurement cell. Finally, a fast approximation method for posterior probability density is proposed based on Gibbs sampling, which improves the accuracy and efficiency of the data association. Simulation results show that the proposed algorithm can effectively estimate multiple extended target states of different shapes, and provide stable cardinality estimation in the clutter environment compared to traditional multiple extended target tracking.
-
算法1 吉布斯采样算法 输入:$ {\gamma ^{(1)}},{T_{\text{G}}},\eta ({\gamma _i}) $ 输出:$ {\gamma ^{(1)}},{\gamma ^{(2)}}, \cdots ,{\gamma ^{({T_{\text{G}}})}} $ 初始化:$ c = [ - 1,0, \cdots ,|{\mathcal{U}}({{\mathbf{Z}}_k})|] $; $ \hat \eta = [\eta ( - 1),\eta (0), \cdots ,\eta (|{\mathcal{U}}({{\mathbf{Z}}_k})|)] $; for $ t = 2,3, \cdots ,{T_{\text{G}}} $ do $ {\gamma ^{(t)}} = [{\text{ }}] $; for $m = 1,2, \cdots ,|{{\boldsymbol{\varXi}} _{k - 1} }| + |{ {\mathbf{B} }_k}|$ do for $ j = 1,2, \cdots ,|{\mathcal{U}}({{\mathbf{Z}}_k})| $ do $ {\hat \eta _m}(j) = {\eta _m}(j) $$(1 - {1_{\{ \gamma _{1:m - 1}^{(t)},\gamma _{m + 1:|{{\boldsymbol{\varXi}} _{k - 1} }| + |{ {\mathbf{B} }_k}|}^{(t - 1)}\} } }(j))$; end for $ \gamma _m^{(t)} \sim {\text{Categorical}}(c,{\hat \eta _m}) $; end for ${\gamma ^{(t)} } = [\gamma _1^{(t)},\gamma _2^{(t)}, \cdots ,\gamma _{|{\varXi _{k - 1} }| + |{ {\mathbf{B} }_k}|}^{(t)}]$; end for 表 1 不同杂波数目下,GPR-GLMB和JL-GLMB滤波器跟踪性能对比(GPR-GLMB/JL-GLMB)
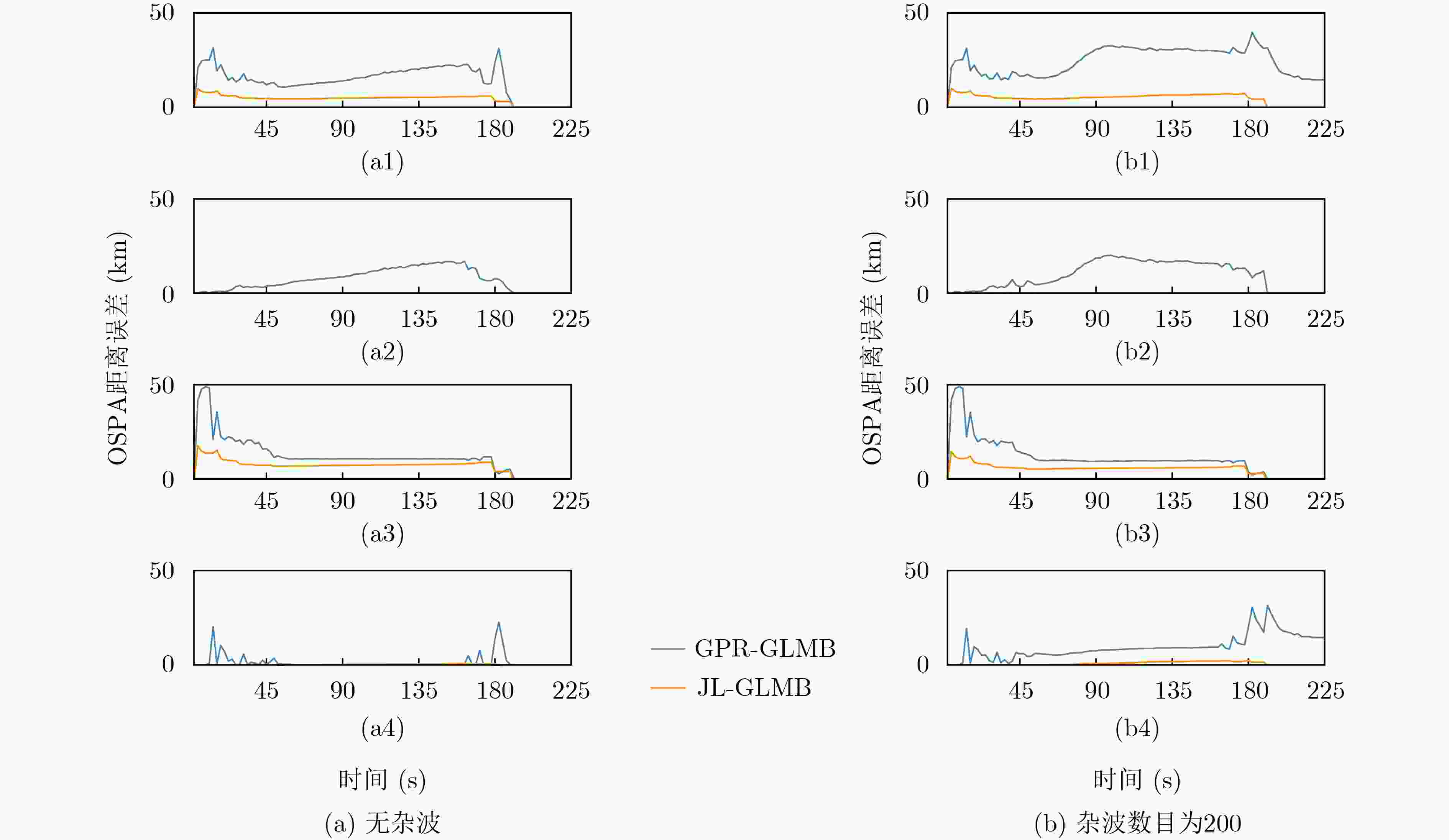
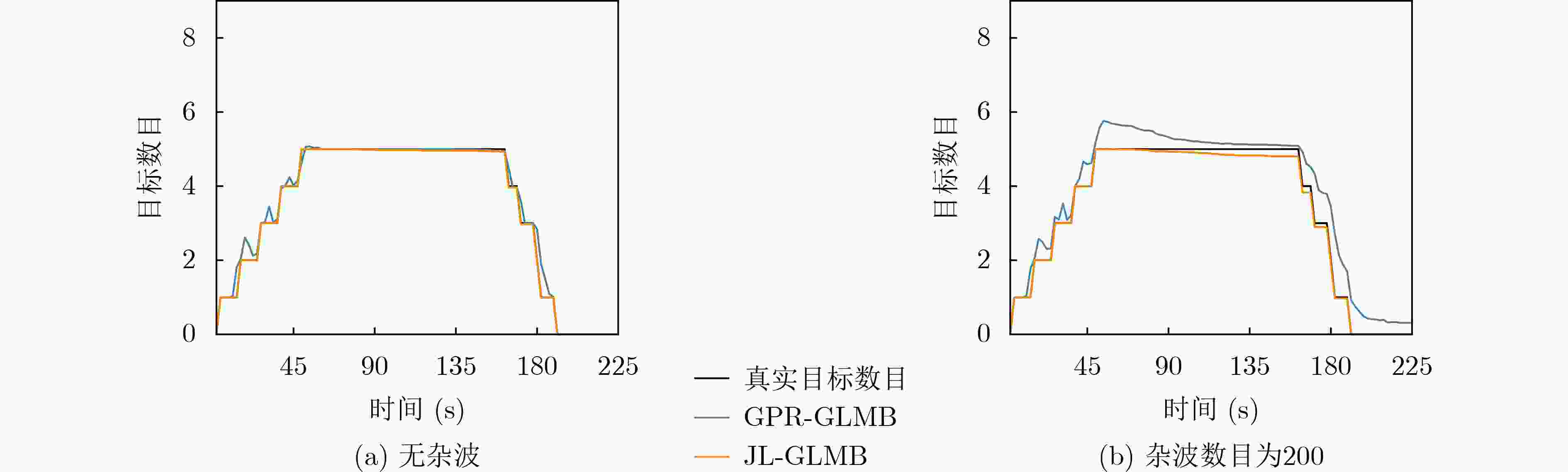
杂波数目 0 50 100 150 200 OSPA距离 14.096 8/4.335 7 16.660 1/4.459 5 19.272 8/4.594 5 21.759 7/4.701 5 24.350 1/4.830 6 位置误差 6.965 0/0.012 8 7.568 7/0.013 2 8.179 7/0.013 3 8.756 7/0.014 0 9.340 3/0.014 6 形状误差 10.807 8/8.154 2 11.091 9/8.181 5 11.255 9/8.210 8 11.435 0/8.278 2 11.644 1/8.297 5 势误差 1.290 0/0.186 0 3.365 8/0.327 5 5.421 5/0.469 0 7.493 6/0.604 2 9.553 0/0.842 0 -
[1] YU Miao, GONG Liyun, OH H, et al. Multiple model ballistic missile tracking with state-dependent transitions and gaussian particle filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1066–1081. doi: 10.1109/TAES.2017.2773258 [2] 李文娟, 顾红, 苏卫民. 基于多伯努利概率假设密度的扩展目标跟踪方法[J]. 电子与信息学报, 2016, 38(12): 3114–3121. doi: 10.11999/JEIT160372LI Wenjuan, GU Hong, and SU Weimin. Extended target tracking method based on Multi-Bernoulli probability hypothesis density[J]. Jounal of Electronics &Information Technology, 2016, 38(12): 3114–3121. doi: 10.11999/JEIT160372 [3] YU Le, ZUO Yanchun, LIU Songhua, et al. False scattering center extraction based on template matching method[J]. IEEE Antennas and Wireless Propagation Letters, 2022, 21(4): 720–724. doi: 10.1109/LAWP.2022.3143868 [4] 何祥宇, 李静, 杨数强, 等. 基于ET-PHD滤波器和变分贝叶斯近似的扩展目标跟踪算法[J]. 计算机应用, 2020, 40(12): 3701–3706. doi: 10.11772/j.issn.1001-9081.2020040451HE Xiangyu, LI Jing, YANG Shuqiang, et al. Extended target tracking algorithm based on ET-PHD filter and variational Bayesian approximation[J]. Journal of Computer Applications, 2020, 40(12): 3701–3706. doi: 10.11772/j.issn.1001-9081.2020040451 [5] RUUD K A, BREKKE E F, and EIDSVIK J. LIDAR extended object tracking of a maritime vessel using an ellipsoidal contour model[C]. Sensor Data Fusion: Trends, Solutions, Applications, Bonn, Germany, 2018: 1–6. [6] ZHANG Xing, YAN Zhibin, CHEN Yunqi, et al. A novel particle filter for extended target tracking with random hypersurface model[J]. Applied Mathematics and Computation, 2022, 425: 127081. doi: 10.1016/j.amc.2022.127081 [7] AKBARI B and ZHU Haibin. Tracking dependent extended targets using multi-output spatiotemporal Gaussian processes[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(10): 18301–18314. doi: 10.1109/TITS.2022.3154926 [8] KAULBERSCH H, BAUM M, and WILLETT P. EM approach for tracking star-convex extended objects[C]. The 20th International Conference on Information Fusion, Xi'an, China, 2017: 1–7. [9] SUN Lifan, LAN Jian, and LI Xiaorong. Extended target tracking using star-convex model with non-linear inequality constraints[C]. The 31st Chinese Control Conference, Hefei, China, 2012: 3869–3874. [10] AFTAB W, DE FREITAS A, ARVANEH M, et al. A gaussian process convolution particle filter for multiple extended objects tracking with non-regular shapes[C]. The 21st International Conference on Information Fusion, Cambridge, UK, 2018: 1–8. [11] WAHLSTRÖM N and ÖZKAN E. Extended target tracking using gaussian processes[J]. IEEE Transactions on Signal Processing, 2015, 63(16): 4165–4178. doi: 10.1109/TSP.2015.2424194 [12] LIU Yiduo, JI Hongbing, and ZHANG Yongquan. Measurement transformation algorithm for extended target tracking[J]. Signal Processing, 2021, 186: 108129. doi: 10.1016/j.sigpro.2021.108129 [13] QIN Zheng, KIRUBARAJAN T, and LIANG Yangang. Application of an efficient graph-based partitioning algorithm for extended target tracking using GM-PHD filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(6): 4451–4466. doi: 10.1109/TAES.2020.2990803 [14] GRANSTROM K and ORGUNER U. A PHD filter for tracking multiple extended targets using random matrices[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5657–5671. doi: 10.1109/TSP.2012.2212888 [15] LUNDQUIST C, GRANSTRÖM K, and ORGUNER U. An extended target CPHD filter and a gamma gaussian inverse wishart implementation[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 472–483. doi: 10.1109/JSTSP.2013.2245632 [16] VO B T and VO B N. Labeled random finite sets and multi-object conjugate priors[J]. IEEE Transactions on Signal Processing, 2013, 61(13): 3460–3475. doi: 10.1109/TSP.2013.2259822 [17] BEARD M, REUTER S, GRANSTRÖM K, et al. A generalised labelled multi-bernoulli filter for extended multi-target tracking[C]. The 18th International Conference on Information Fusion, Washington, USA, 2015: 991–998. [18] 陈辉, 李国财, 韩崇昭, 等. 高斯过程回归模型多扩展目标多伯努利滤波器[J]. 控制理论与应用, 2020, 37(9): 1931–1943. doi: 10.7641/CTA.2020.90978CHEN Hui, LI Guocai, HAN Chongzhao, et al. A multiple extended target multi-Bernouli filter based on Gaussian process regression model[J]. Control Theory &Applications, 2020, 37(9): 1931–1943. doi: 10.7641/CTA.2020.90978 [19] SCHEEL A, REUTER S, and DIETMAYER K. Using separable likelihoods for laser-based vehicle tracking with a labeled multi-bernoulli filter[C]. The 19th International Conference on Information Fusion, Heidelberg, Germany, 2016: 1200–1207. [20] LI Fu, SHUGUROV I, BUSAM B, et al. PolarMesh: A star-convex 3D shape approximation for object pose estimation[J]. IEEE Robotics and Automation Letters, 2022, 7(2): 4416–4423. doi: 10.1109/LRA.2022.3147880 [21] 陈彦锡, 郭琨毅, 殷红成, 等. 复杂场景散射中心模型化与雷达成像应用[J]. 系统工程与电子技术, 2021, 43(10): 2733–2741. doi: 10.12305/j.issn.1001-506X.2021.10.05CHEN Yanxi, GUO Kunyi, YIN Hongcheng, et al. Scattering center modeling and radar imaging application in complex scenes[J]. Systems Engineering and Electronics, 2021, 43(10): 2733–2741. doi: 10.12305/j.issn.1001-506X.2021.10.05 [22] 王碧垚, 王永齐, 顾鹏. 考虑形状差异的RFS多目标跟踪性能评估方法[J]. 火力与指挥控制, 2021, 46(5): 58–63. doi: 10.3969/j.issn.1002-0640.2021.05.011WANG Biyao, WANG Yongqi, and GU Peng. Performance evaluation considering shape difference for multi-target tracking based on random finite set[J]. Fire Control &Command Control, 2021, 46(5): 58–63. doi: 10.3969/j.issn.1002-0640.2021.05.011 -





 下载:
下载:


 下载:
下载:
