Entangled Light Quantum Positioning Method Based on Adaptive Light Source Selection
-
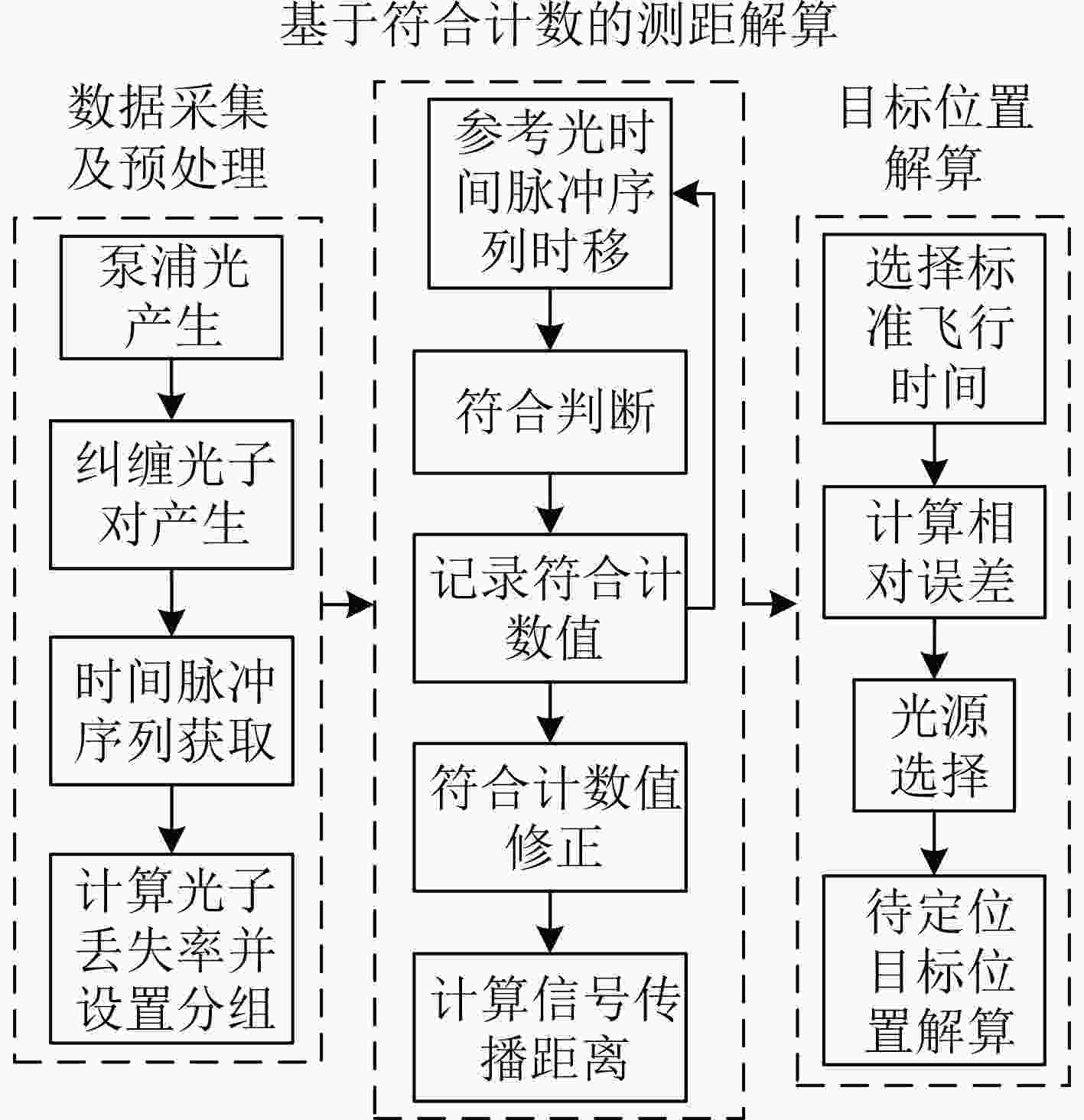
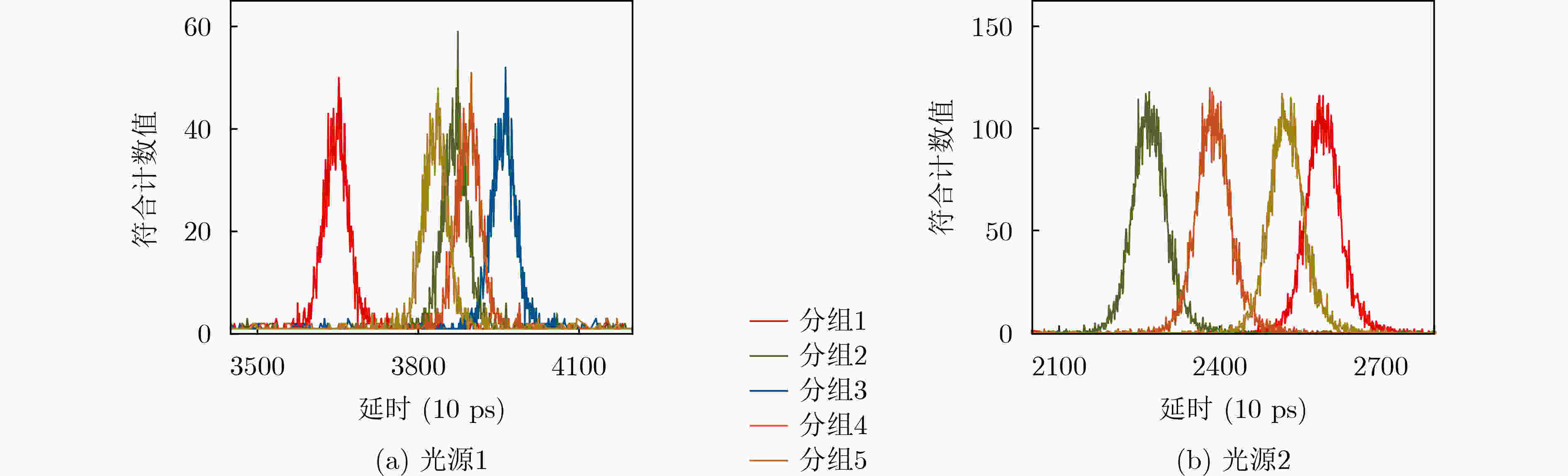
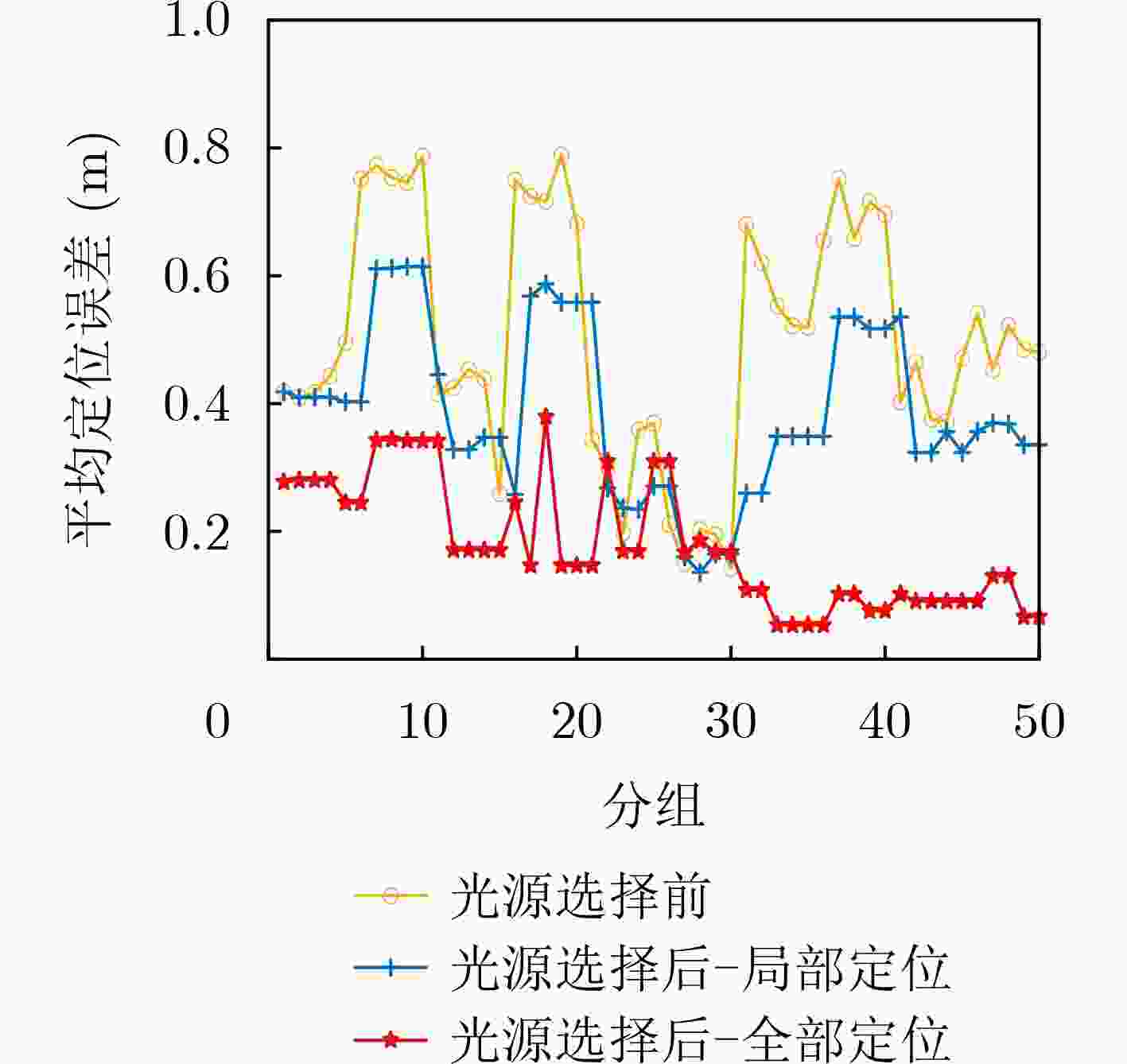
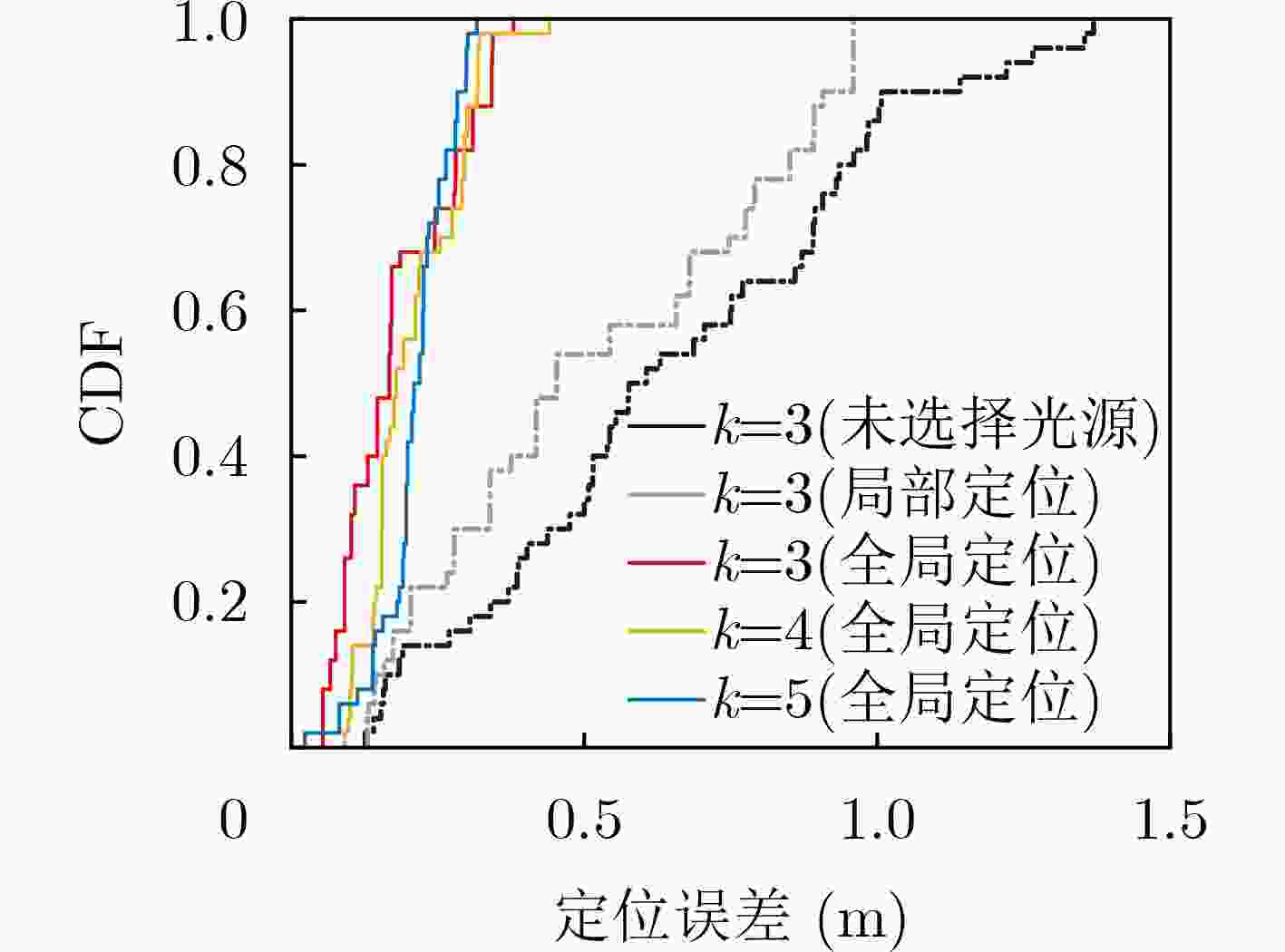
摘要: 纠缠光量子定位方法是目前导航与定位领域的研究热点之一,而现有方法很少考虑散射环境动态变化对不同光源中传播距离估计性能的影响,从而导致定位精度不高且鲁棒性较差的问题。针对这一问题,该文提出一种基于自适应光源选择的纠缠光量子定位方法。首先,建立不同散射环境干扰与各光源信号传播距离之间的数学关系,计算各光源信号光时间脉冲序列光子丢失率均值,并对各光源时间脉冲序列进行动态分组;其次,对纠缠光时间脉冲序列进行符合计数,根据光的2阶关联曲线得到各光源各分组下的传播距离;最后,以各光源各分组下的相对误差为依据,动态选择具有较小相对误差的光源进行定位。实验结果表明,所提方法具有更高的定位精度和更强的定位鲁棒性。Abstract: The entangled photon positioning method is one of the current research hotspots in the field of navigation and positioning. However, the existing methods consider rarely the influence of the dynamic changes of the scattering environment on the performance of propagation distance estimation in different light sources, resulting in the problem of low positioning accuracy and poor robustness. To solve this problem, an entangled light quantum positioning method is proposed based on adaptive light source selection. First of all, the mathematical relationship between the interference of different scattering environments and the light propagation distance in each light source is established, the average photon loss rate of each light source signal light time pulse sequence is calculated, and the time pulse sequence of each light source is dynamically grouped. Then, the optical time pulse sequence is matched, and the propagation distance of each light source in each group is obtained according to the second-order correlation curve of light. Finally, based on the relative error of each light source in each group, the light source with the smaller relative error in each group is dynamically selected for positioning. The experimental results show that the proposed method has high positioning accuracy and strong positioning robustness.
-
表 1 基于自适应光源选择的纠缠光量子定位算法
输入:$\left\{ {\bf{CH1} }_{1},{\bf{CH1} }_{2},\cdots ,{\bf{CH1} }_{A}\right\}$,$\left\{{{\bf{CH2}}}_{1},{\bf{CH2}}_{2},\cdots ,{\bf{CH2}}_{A}\right\}$,$ K $,$ B $,$M$,$T$,$ s $,$ Q $,$ {g_\tau } $ 输出:各分组下选择的定位光源$\left\{ { { {\boldsymbol{v} }_1},{ {\boldsymbol{v} }_2}, \cdots ,{ {\boldsymbol{v} }_M} } \right\}$,其中,第.$m$.个分组下定位光源${{\mathbf{v}}_m} = \left( {{v_1},{v_2}, \cdots ,{v_B}} \right)$ (1) for $q = 1:Q$ do (2) $ {\tau _q} = s \times q $,${\bf{count}}\left( { {\tau _q} } \right) \leftarrow 0$ (3) for $i = 1:\dfrac{K}{M}$ do (4) If $\left| { {t_{1i} } + {\tau _q} - {t_{2i} } } \right| \le {g_\tau }$ do (5) ${\rm{count} }\left( { {\tau _q} } \right) = {\rm{count} }\left( { {\tau _q} } \right) + 1$ (6) end if (7) end for (8) end for (9) ${\text{find} }({\bf{count} }(\tau ) = = \max ({\bf{count} }({\tau _q})))$ (10) 重复式(1)-式(9)$A \cdot M$次,得到$\left\{ { {{\boldsymbol{\tau}} _1},{{\boldsymbol{\tau}} _2}, \cdots ,{{\boldsymbol{\tau}} _M} } \right\}$,${{\boldsymbol{\tau}} _m}{\text{ = } }\left( { {\tau _1},{\tau _2}, \cdots ,{\tau _A} } \right)$ (11) 计算${{\boldsymbol{\tau}} _m}{\left( a \right)^\prime }{\text{ = } }{{\boldsymbol{\tau}} _m}\left( a \right) - {{\boldsymbol{\tau}} _s}$,${{\boldsymbol{\tau}} _s}{\text{ = } }\min \left( {{\boldsymbol{\tau}} \left( a \right)} \right)$ (12) 记录各分组下$ B $个误差最小定位光源$\left\{ { { {\boldsymbol{w} }_1},{ {\boldsymbol{w} }_2}, \cdots ,{ {\boldsymbol{w} }_M} } \right\}$,${ {\boldsymbol{w} }_m} = \left( { {w_1},{w_2}, \cdots ,{w_B} } \right)$ (13) if $ {\tau }_{m}\left({w}_{m}\left(b\right)\right) < {\tau }_{m}\left({w}_{m}\left(b-1\right)\right) $ (14) ${ {\boldsymbol{v} }_m}{\text{ = } }{ {\boldsymbol{v} }_m} \cup {w_m}\left( b \right)$ (15) end if (16) 重复式(13)-式(15)$B \cdot M$次,更新各分组定位光源$\left\{ { { {\boldsymbol{v} }_1},{ {\boldsymbol{v} }_2}, \cdots ,{ {\boldsymbol{v} }_M} } \right\}$,${{\mathbf{v}}_m} = \left( {{v_1},{v_2}, \cdots ,{v_B}} \right)$ 表 2 实验主要参数
名称 取值 激光器功率(mW) 40 非线性晶体尺寸(mm3) 1×2×20 温度控制器精度(°C) 0.01 同步与符合模块时间测量范围(ms) ≥1 单光子探测器死时间(ns) ≤20 单光子探测器暗计数(Hz) <500 单光子探测器饱和计数(MHz) 35 单光子探测器探测效率 >60% 单光子时间分辨率(ps) 350 -
[1] S G F. Newton's mechanics and its influence on the formation of modern physics[J]. Journal of the Franklin Institute, 1927, 204(3): 433–434. doi: 10.1016/S0016-0032(27)92147-4 [2] 朱方悦. 麦克斯韦方程组的简单概述及应用[J]. 中国新通信, 2018, 20(15): 230–231. doi: 10.3969/j.issn.1673-4866.2018.15.189ZHU Fangyue. Brief overview and application of Maxwell equations[J]. China New Telecommunications, 2018, 20(15): 230–231. doi: 10.3969/j.issn.1673-4866.2018.15.189 [3] LU Chenguang. A generalization of Shannon’s information theory[J]. International Journal of General Systems, 1999, 28(6): 453–490. doi: 10.1080/03081079908935247 [4] SPICER D F and SACKETT J N. Shot noise limits to measurement accuracy and bandwidth in electron-beam testing[J]. Journal of Vacuum Science & Technology B:Microelectronics and Nanometer Structures, 1986, 4(1): 213. doi: 10.1116/1.583441 [5] ZHAO Fa, WANG Dong, and YE Liu. Relationship between entanglement and coherence in some two-qubit states[J]. International Journal of Theoretical Physics, 2022, 61(1): 10. doi: 10.1007/s10773-022-05014-z [6] FORTIN S and LOMBARDI O. Entanglement and indistinguishability in a quantum ontology of properties[J]. Studies in History and Philosophy of Science, 2022, 91: 234–243. doi: 10.1016/j.shpsa.2021.11.017 [7] FAN Chenrui, LU Bo, FENG Xueting, et al. Efficient multi-qubit quantum data compression[J]. Quantum Engineering, 2021, 3(2): e67. doi: 10.1002/que2.67 [8] LIU Kui, LI Jiaming, YANG Rongguo, et al. High-fidelity heralded quantum squeezing gate based on entanglement[J]. Optics Express, 2020, 28(16): 23628–23639. doi: 10.1364/OE.398096 [9] GIOVANNETTI V, LLOYD S, and MACCONE L. Positioning and clock synchronization through entanglement[J]. Physical Review A, 2002, 65(2): 022309. doi: 10.1103/PhysRevA.65.022309 [10] LUKIN I P, RYCHKOV D S, FALITS A V, et al. A phase screen model for simulating numerically the propagation of a laser beam in rain[J]. Quantum Electronics, 2009, 39(9): 863–868. doi: 10.1070/QE2009v039n09ABEH013789 [11] 聂敏, 任杰, 杨光, 等. PM2.5大气污染对自由空间量子通信性能的影响[J]. 物理学报, 2015, 64(15): 150301. doi: 10.7498/aps.64.150301NIE min, REN Jie, YANG Guang, et al. Influences of PM2.5 atmospheric pollution on the performance of free space quantum communication[J]. Acta Physica Sinica, 2015, 64(15): 150301. doi: 10.7498/aps.64.150301 [12] 张秀再, 徐茜, 刘邦宇. 雾对自由空间量子通信性能的影响[J]. 光学学报, 2020, 40(7): 0727001. doi: 10.3788/AOS202040.0727001ZHANG Xiuzai, XU Qian, and LIU Bangyu. Effect of fog on the performance of free space quantum communication[J]. Acta Optica Sinica, 2020, 40(7): 0727001. doi: 10.3788/AOS202040.0727001 [13] 丛爽, 吴文燊, 尚伟伟, 等. 削弱大气干扰影响的三种量子测距定位方案[J]. 中国科学技术大学学报, 2020, 50(1): 64–71. doi: 10.3969/j.issn.0253-2778.2020.01.008CONG Shuang, WU Wenshen, SHANG Weiwei, et al. Three quantum ranging and positioning schemes to reduce atmospheric interferences[J]. Journal of University of Science and Technology of China, 2020, 50(1): 64–71. doi: 10.3969/j.issn.0253-2778.2020.01.008 [14] 周政, 安雪碧, 钱泳君, 等. 基于参量下转换的量子纠缠光源仿真模型[J]. 无线电通信技术, 2020, 46(6): 652–657. doi: 10.3969/j.issn.1003-3114.2020.06.005ZHOU Zheng, AN Xuebi, QIAN Yongjun, et al. Simulation model of type-I quantum entangled light source based on BBO crystal[J]. Radio Communications Technology, 2020, 46(6): 652–657. doi: 10.3969/j.issn.1003-3114.2020.06.005 [15] GRICE W P and WALMSLEY I A. Spectral information and distinguishability in type-II down-conversion with a broadband pump[J]. Physical Review A, 1997, 56(2): 1627–1634. doi: 10.1103/PhysRevA.56.1627 [16] 丛爽, 宋媛媛. 量子定位系统中符合计数与到达时间差的获取[J]. 北京航空航天大学学报, 2020, 46(10): 1834–1843. doi: 10.13700/j.bh.1001-5965.2019.0540CONG Shuang and SONG Yuanyuan. Coincidence counting and acquisition of the time difference of arrival in quantum positioning systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(10): 1834–1843. doi: 10.13700/j.bh.1001-5965.2019.0540 [17] KWIAT P G, STEINBERG A M, and CHIAO R Y. High-visibility interference in a Bell-inequality experiment for energy and time[J]. Physical Review A, 1993, 47(4): R2472–R2475. doi: 10.1103/physreva.47.r2472 -





 下载:
下载:


 下载:
下载:
