Energy Efficiency Optimization Algorithm of Cooperative Non-Orthogonal Multiple Access joint Simultaneous Wireless Information and Power Transfer Based on Successive Convex Approximation
-
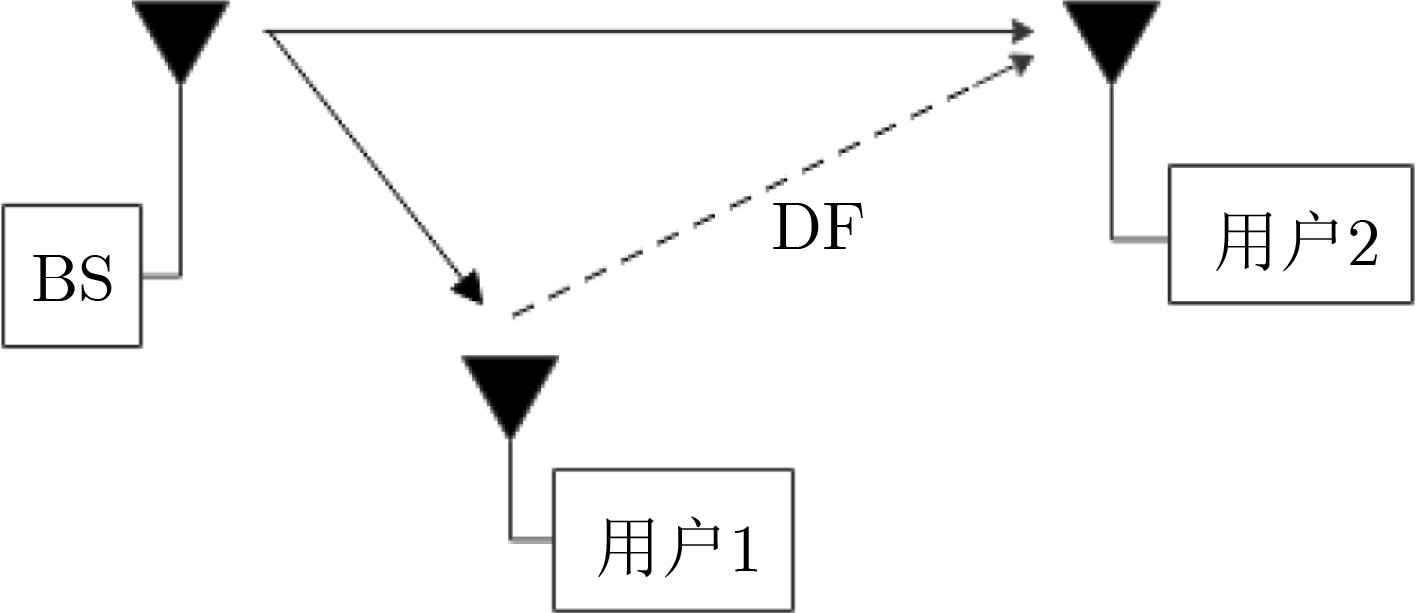
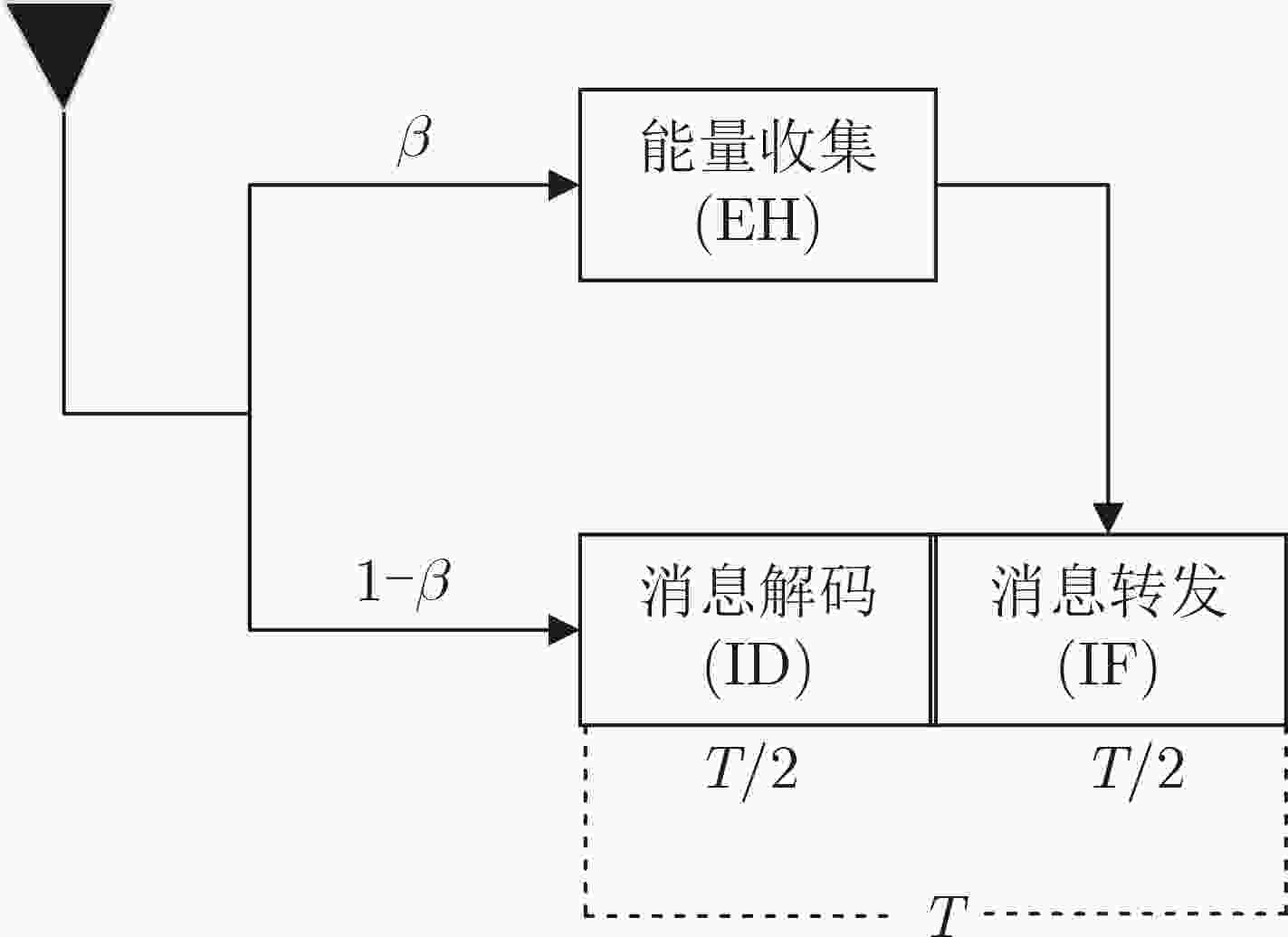
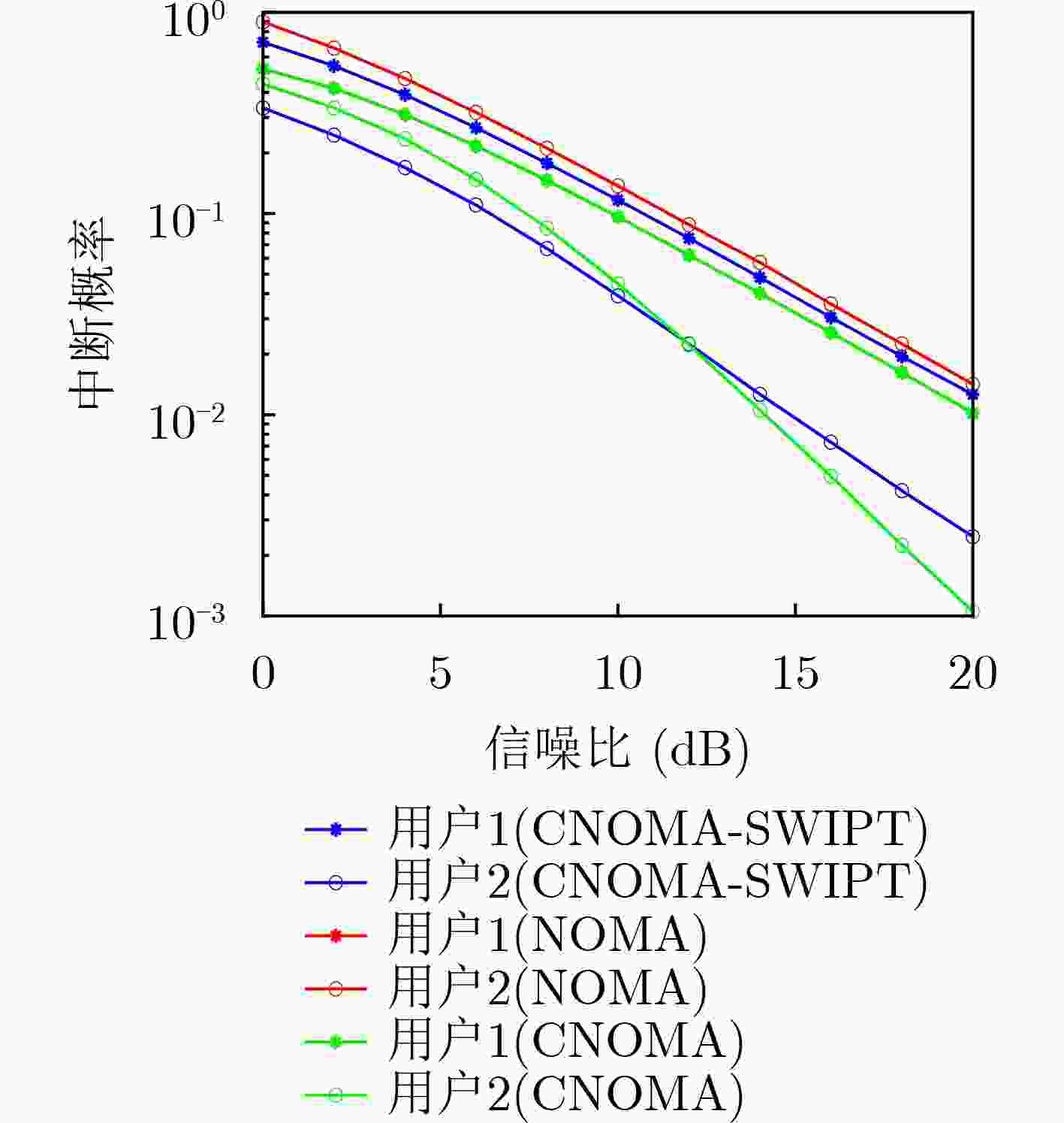
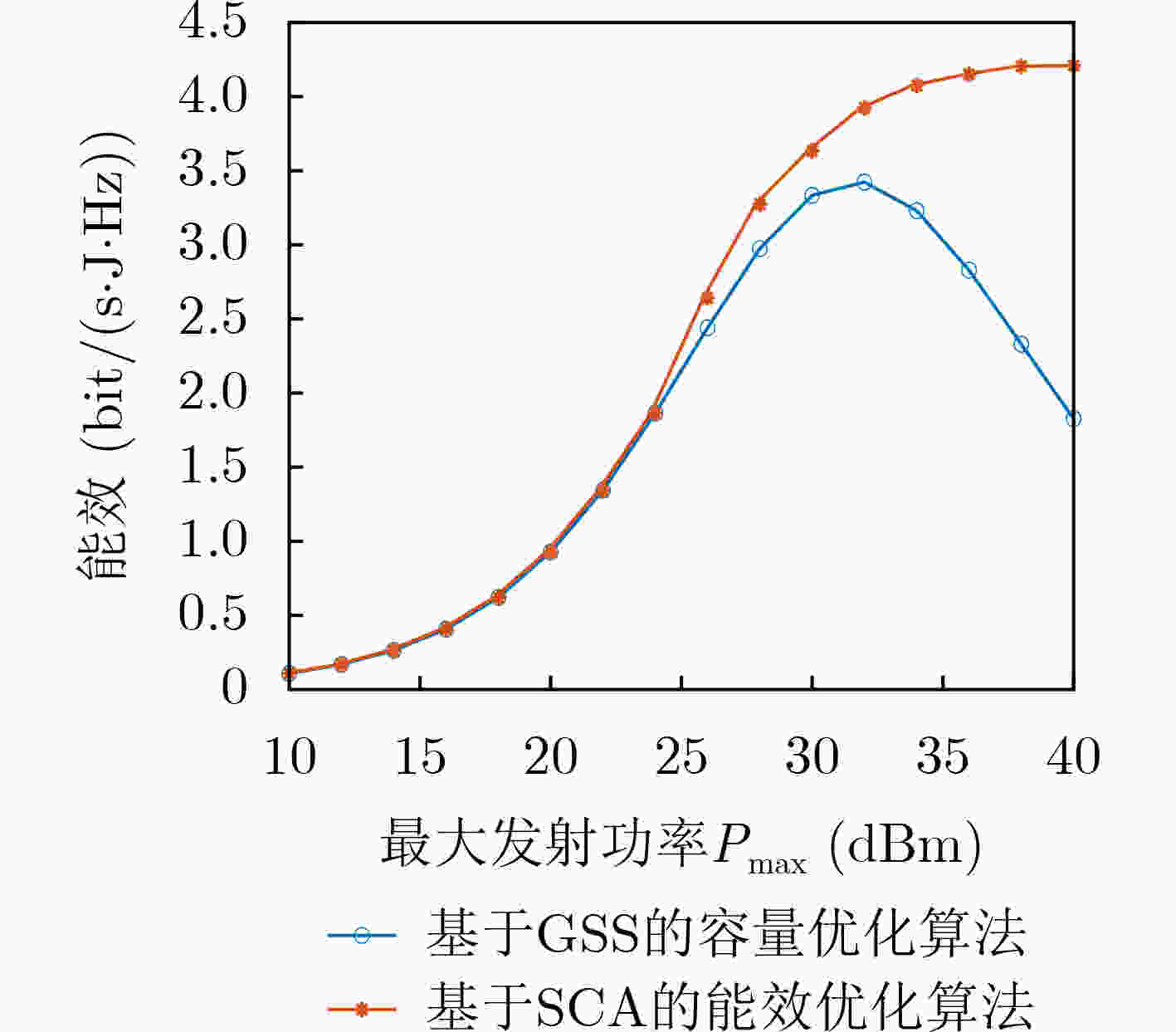
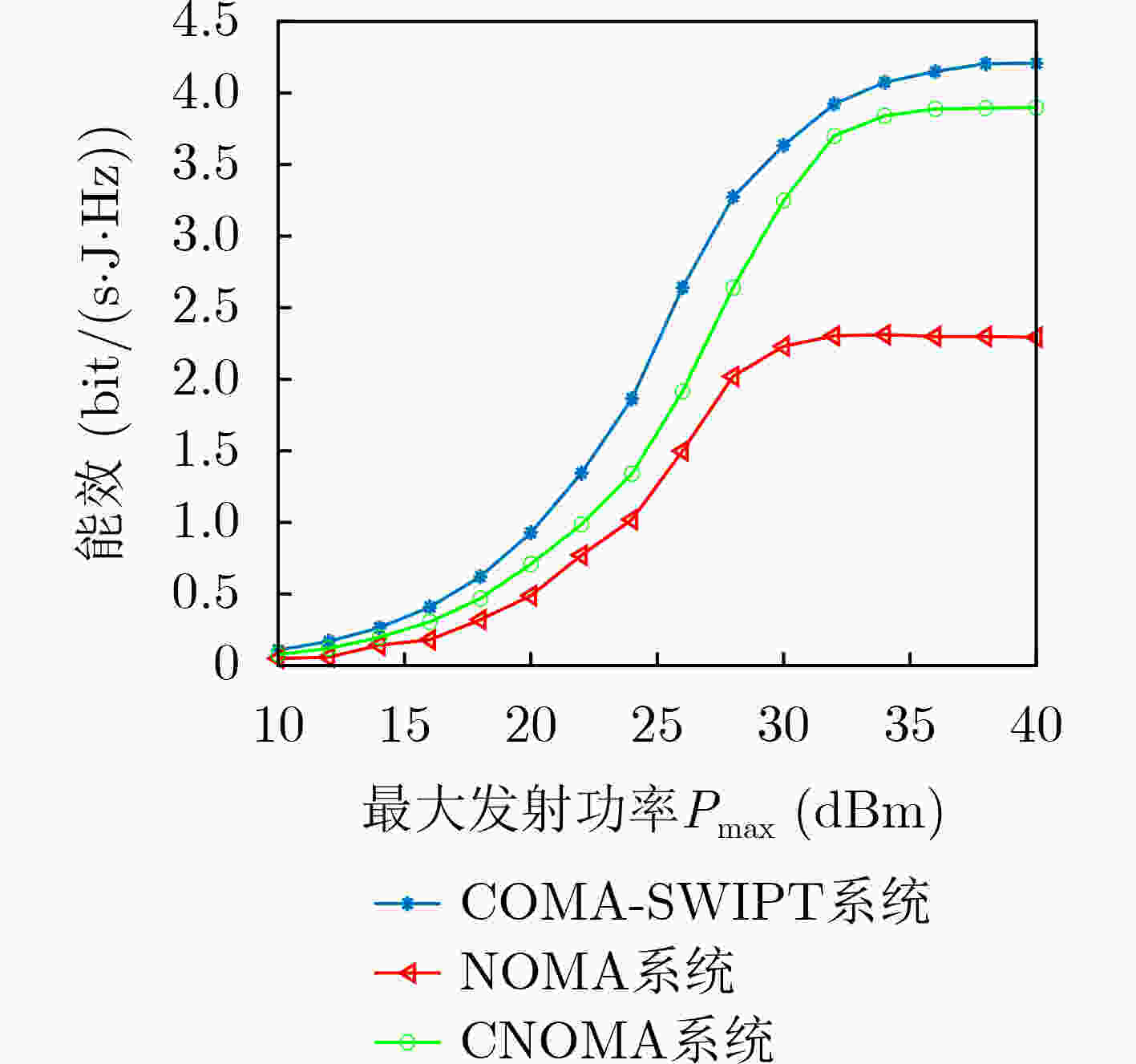
摘要: 在传统的非正交多址(NOMA)系统中,通常将更多的功率分配给边缘用户以此来保证其通信质量,系统公平性以牺牲系统容量为代价。基于协作通信的NOMA系统虽可解决上述问题,但在协作阶段中心用户需承担中继的作用,这种方式必将给中心用户带来一定的负担。为了兼顾系统容量和公平性,该文提出一种基于协作通信和无线携能通信(SWIPT)的新型资源分配方案,该方案在满足边缘用户通信质量情况下,使用能量收集设备完成能量收集,通过连续凸逼近(SCA)求解目标问题最大化系统能效。仿真结果表明,与传统NOMA和协作式非正交多址接入系统(CNOMA)相比,CNOMA-SWIPT系统的能量效率得到了较大的提高,在基站最大发射功率为30 dBm时相比NOMA系统能达到60.8%的增益,相比CNOMA系统能达到比CNOMA系统高出约11.5%的增益,更符合绿色通信的发展理念。Abstract: In a traditional Non-Orthogonal Multiple Access (NOMA) system, more power is usually allocated to edge users to ensure its communication quality. However, the fairness of the system comes at the expense of system capacity. Introducing collaborative communication into the NOMA system, the central user also needs to assume the role of relay in the collaboration phase. This method will inevitably bring a certain burden to the central user. In order to balance system capacity and fairness, a new resource allocation scheme based on cooperative communication and Simultaneous Wireless Information and Power Transfer (SWIPT) is proposed. Energy harvesting equipment is used for energy harvesting, and maximizes the energy efficiency of the system by solving the target problem through Successive Convex Approximation (SCA). Compared with the traditional NOMA and Cooperative NOMA, the energy efficiency of the CNOMA-SWIPT system is greatly improved. When the maximum transmit power of the base station is 30 dBm, CNOMA-SWIPT can achieve a gain of 60.8% compared to the NOMA system and can achieve a gain of about 11.5% higher than that of the CNOMA system, which is more in line with the development concept of green communication.
-
算法1 Dinkelbach分数规划 初始化:迭代次数n=0,准许误差$\epsilon={10}^{-4}$, $ {\lambda }^{n}=0 $ 若F($ \lambda $)=$ {R}_{\mathrm{s}\mathrm{u}\mathrm{m}} $–${\lambda }^{n}{P}_{\mathrm{s}\mathrm{u}\mathrm{m} }\ge \epsilon$,则执行: 用$ {\lambda }^{n} $求解max ($ {R}_{\mathrm{s}\mathrm{u}\mathrm{m}} $–$ {\lambda }^{n}{P}_{\mathrm{s}\mathrm{u}\mathrm{m}} $) ; 更新$ {R}_{\mathrm{s}\mathrm{u}\mathrm{m}} $–$ {\lambda }^{n}{P}_{\mathrm{s}\mathrm{u}\mathrm{m}} $, $ {\lambda }^{n} $, n=n+1; 否则:$ {{\eta }_{\mathrm{E}\mathrm{E}}}^{*}={\lambda }^{n} $ 算法2 基于SCA的P2求解算法 初始化:迭代次数j=1,${a}_{i} ^{j} {,b}_{i} ^{j}$=0(i=1,2,3),$\varDelta $=1,准许误差
$ \epsilon={10}^{-4} $若$\varDelta\ge \epsilon$,则执行: 通过CVX工具箱求解P2,得到${q}_{1} ^{j}, {q}_{2} ^{j}, {q}_{3} ^{j}, {q}_{4} ^{j}, {q}_{5} ^{j}$ 更新${z}_{i} ^{j} {,b}_{i} ^{j}$,${a}_{i} ^{j} {,b}_{i} ^{j}$ 更新:$\varDelta=|{F\left(\lambda \right)}^{j}-{F\left(\lambda \right)}^{j-1}|$; j=j+1;
否则: 输出$\lambda =\dfrac{ {R}_{\mathrm{s}\mathrm{u}\mathrm{m} }({ {q}_{1} }^{j}, {q}_{2} ^{j}, {q}_{3} ^{j}, {q}_{4} ^{j}, {q}_{5} ^{j})}{ {P}_{\mathrm{s}\mathrm{u}\mathrm{m} }( {q}_{1} ^{j}, {q}_{2} ^{j}, {q}_{3} ^{j}, {q}_{4} ^{j}, {q}_{5} ^{j})}$算法3 基于SCA的CNOMA-SWIPT系统能效优化算法 初始化:迭代次数n=0,准许误差$ \epsilon={10}^{-4} $, $ {\lambda }^{n}=0 $ 若F($ {\lambda }^{n} $)$ \ge \epsilon $,则执行: 设j=0, ${a}_{i}^{j} {,b}_{i} ^{j}$=0(i=1,2,3),$\varDelta=1 $; 若$\varDelta\ge \epsilon$,则执行: 通过CVX工具箱求解P2,得到${q}_{1} ^{j}, {q}_{2} ^{j}, {q}_{3} ^{j}, {q}_{4} ^{j}, {q}_{5} ^{j}$; 更新${z}_{i} ^{j} {,b}_{i} ^{j}$, ${a}_{i} ^{j} {,b}_{i} ^{j}$, $\varDelta=|{F\left(\lambda \right)}^{j}-{F\left(\lambda \right)}^{j-1}|$; j=j +1; 直到$\varDelta < \epsilon$,执行:
F($ {\lambda }^{n} $)=${R}_{\mathrm{s}\mathrm{u}\mathrm{m} }\left( {q}_{1} ^{j}, {q}_{2} ^{j} {q}_{3} ^{j},{ {q}_{4} }^{j}, {q}_{5} ^{j}\right)-{\lambda }^{n}{P}_{\mathrm{s}\mathrm{u}\mathrm{m} }\left( {q}_{1} ^{j}, {q}_{2} ^{j}, {q}_{3} ^{j}, {q}_{4} ^{j}, {q}_{5} ^{j}\right); {\lambda }^{n}=\dfrac{ {R}_{\mathrm{s}\mathrm{u}\mathrm{m} }( {q}_{1} ^{j}, {q}_{2} ^{j}, {q}_{3} ^{j}, {q}_{4} ^{j}, {q}_{5} ^{j})}{ {P}_{\mathrm{s}\mathrm{u}\mathrm{m} }( {q}_{1} ^{j}, {q}_{2} ^{j}, {q}_{3} ^{j}, {q}_{4} ^{j}, {q}_{5} ^{j})}$n=n+1; 若F($ {\lambda }^{n} $)<$ \epsilon $: 输出$\lambda =\dfrac{ {R}_{\mathrm{s}\mathrm{u}\mathrm{m} }( {q}_{1} ^{j}, {q}_{2} ^{j}, {q}_{3} ^{j}, {q}_{4} ^{j}, {q}_{5} ^{j})}{ {P}_{\mathrm{s}\mathrm{u}\mathrm{m} }( {q}_{1} ^{j}, {q}_{2} ^{j}, {q}_{3} ^{j}, {q}_{4} ^{j}, {q}_{5} ^{j})}$ -
[1] DING Zhiguo, YANG Zheng, FAN Pingzhi, et al. On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users[J]. IEEE Signal Processing Letters, 2014, 21(12): 1501–1505. doi: 10.1109/LSP.2014.2343971 [2] HIGUCHI K and KISHIYAMA Y. Non-orthogonal access with random beamforming and intra-beam SIC for cellular MIMO downlink[C]. 2013 IEEE 78th Vehicular Technology Conference, Las Vegas, USA, 2013: 1–5. [3] SHAHAB M B and SHIN S Y. User pairing and power allocation for non-orthogonal multiple access: Capacity maximization under data reliability constraints[J]. Physical Communication, 2018, 30: 132–144. doi: 10.1016/j.phycom.2018.05.010 [4] SHAHAB M B, KADER F, and SHIN S Y. On the power allocation of non-orthogonal multiple access for 5G wireless networks[C]. 2016 International Conference on Open Source Systems & Technologies (ICOSST), Lahore, Pakistan, 2016: 89–94. [5] KIMY B, LIM S, KIM H, et al. Non-orthogonal multiple access in a downlink multiuser beamforming system[C]. MILCOM 2013 - 2013 IEEE Military Communications Conference, San Diego, USA, 2014: 1278–1283. [6] DING Zhiguo, PENG Mugen, and POOR H V. Cooperative non-orthogonal multiple access in 5G systems[J]. IEEE Communications Letters, 2015, 19(8): 1462–1465. doi: 10.1109/LCOMM.2015.2441064 [7] KRIKIDIS I, TIMOTHEOU S, NIKOLAOU S, et al. Simultaneous wireless information and power transfer in modern communication systems[J]. IEEE Communications Magazine, 2014, 52(11): 104–110. doi: 10.1109/MCOM.2014.6957150 [8] GUO Shengjie, ZHOU Xiangwei, and ZHOU Xiangyun. Energy-efficient resource allocation in SWIPT cooperative wireless networks[J]. IEEE Systems Journal, 2020, 14(3): 4131–4142. doi: 10.1109/JSYST.2019.2961001 [9] LIU Yuanwei, DING Zhiguo, ELKASHLAN M, et al. Cooperative non-orthogonal multiple access with simultaneous wireless information and power transfer[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 938–953. doi: 10.1109/JSAC.2016.2549378 [10] ZHANG Zhenwei, QU Hua, ZHAO Jihong, et al. Energy efficient transmission design of cooperative NOMA with SWIPT network[C]. 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 2019: 566–572. [11] RAUNIYAR A, ENGELSTAD P E, and ØSTERBØ O N. On the performance of bidirectional NOMA-SWIPT enabled IoT relay networks[J]. IEEE Sensors Journal, 2021, 21(2): 2299–2315. doi: 10.1109/JSEN.2020.3018905 [12] LEE C, JANG G, and CHO S. Energy-efficient adaptive directional queue-stable stochastic scheduling for SWIPT in NOMA[C]. 2020 International Conference on Information Networking (ICOIN), Barcelona, Spain, 2020: 76–79. [13] PARIHAR A S, SWAMI P, BHATIA V, et al. Performance analysis of SWIPT enabled cooperative-NOMA in heterogeneous networks using carrier sensing[J]. IEEE Transactions on Vehicular Technology, 2021, 70(10): 10646–10656. doi: 10.1109/TVT.2021.3110806 [14] TANG Jie, LUO Jingci, LIU Mingqian, et al. Energy efficiency optimization for NOMA with SWIPT[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(3): 452–466. doi: 10.1109/JSTSP.2019.2898114 [15] NGUYEN V D and SHIN O S. An efficient design for NOMA-assisted MISO-SWIPT systems with AC computing[J]. IEEE Access, 2019, 7: 97094–97105. doi: 10.1109/ACCESS.2019.2928877 [16] BUDHIRAJA I, KUMAR N, TYAGI S, et al. An energy-efficient resource allocation scheme for SWIPT-NOMA based femtocells users with imperfect CSI[J]. IEEE Transactions on Vehicular Technology, 2020, 69(7): 7790–7805. doi: 10.1109/TVT.2020.2991466 [17] YUAN Yi, XU Yanqing, YANG Zheng, et al. Energy efficiency optimization in full-duplex user-aided cooperative SWIPT NOMA systems[J]. IEEE Transactions on Communications, 2019, 67(8): 5753–5767. doi: 10.1109/TCOMM.2019.2914386 [18] RAZAVIYAYN M. Successive convex approximation: Analysis and applications[D]. [Ph. D. dissertation], University of Minnesota, 2014. -





 下载:
下载:


 下载:
下载:
