Prediction and Compensation Method of Robot Positioning Error Based on Spatio-temporal Graph Convolution Neural Network
-
摘要: 工业机器人作为智能制造的重要载体，在大范围复杂任务中具有巨大潜力。但是，定位精度低且难以控制的问题阻碍了机器人在高精度任务的进一步推广。为了提升机器人作业精度，该文提出一种基于时空混合图卷积网络的机器人定位误差预测及补偿方法。首先通过设计图关系编码模块、时空混合特征解码模块，构建基于图卷积网络的机器人位姿误差预测模型；然后，针对传统迭代补偿方法中机器人逆解次数多导致效率低的问题，该文将定位误差补偿问题转化为优化问题，并利用遗传算法同时对位置和姿态进行误差补偿；最后，通过拉丁超立方抽样方法获得训练集，实现机器人定位误差预测模型的训练，并通过实验验证了定位误差预测的准确性以及补偿的效果。Abstract: As an important carrier of intelligent manufacturing, industrial robot has great potential in large-scale and complex tasks. However, the problem of low positioning accuracy and difficulty to control hinders the further popularization of robots in high-precision tasks. In order to improve the accuracy of robot operation, a robot positioning error prediction and compensation method based on spatio-temporal convolution graph network is proposed in this work. Firstly, through the design of graph relation coding module and spatio-temporal feature decoding module, the prediction model of the robot position and orientation error based on graph convolution network is constructed; Then, to solve the problem of low efficiency caused by too many times of robotic inverse kinematics solution in traditional iteration compensation methods, the problem of compensation for positioning errors is transformed into optimization problem, and the genetic algorithm is used to compensate the position and attitude errors simultaneously; Finally, the training set is obtained by Latin hypercube sampling method to realize the training of robot positioning error prediction model, and the accuracy of positioning error prediction and the effect of compensation are verified by the experiments.
-
1. 引言
高质量的制造技术是推动经济增长的重中之重，得到制造业市场的进一步关注[1]。工业机器人作为智能制造的重要载体[2]，具有工作空间大、加工柔性强、可在不同场景快速进行配置等优势。另外，相比数控机床，工业机器人自由度多，且可以通过变位机、移动平台等进行拓展，加工灵活性极高，在大型复杂构件的制造中具有巨大的发展潜力。在满足加工质量要求的情况下，机器人加工能达到降低成本、提高效率的效果[3]。
然而，由于机器人关节处的装配误差以及由齿轮间隙和变形引起的误差，使得机器人末端刀具中心点(TCP)的实际位置与编程设定的理想位置存在偏差，严重影响加工质量。该偏差称为机器人的绝对定位误差。一般来说，工业机器人的绝对定位精度低于±1 mm[4]，使得机器人的作业精度低，难以满足高精度工艺需求，限制了机器人在高精加工、精准操作等领域的进一步应用与推广。由于机器人结构的影响，机器人的定位精度会随着机器人在整个工作空间的位置和姿态变化而变化[5]。通常，在机器人作业前，会标定基坐标系，并在此坐标系下进行作业，从而减少了一部分的绝对定位误差。但是，在机器人的大型复杂构件加工等大范围复杂任务中，机器人需要进行大幅度的位置和姿态变化，使其定位误差的大小及方向均发生大幅度变化，致使加工精度的控制变得异常困难。
对此，国内外学者对机器人绝对定位误差的预测和抑制进行了大量的研究工作。在机器人定位误差辨识通常采用机器人几何参数标定的方法，机器人的定位误差的标定可以分为模型标定[6]和无模型标定[7]。模型标定是当前较为常用的方法，首先通过建立的机器人参数模型，如DH模型(Denavit - Hartenberg)、改进DH模型以及PoE(Product of Exponential)模型[8]等，然后根据最小位置误差原理或最小距离误差原理进行机器人实际几何参数标定，从而分析实际与理论之间的误差情况。但是，这种方法一般将机器人看作理想的连杆模型，忽略了占总误差近20%的非几何误差[9]，包括齿轮间隙、装配误差、热效应等。文献[10]指出，经典的基于模型的机器人定位误差标定方法只考虑了恒定的几何误差，忽略了轴承系统和齿轮的不均匀性等更为复杂的非几何误差，导致定位误差预测效果受到限制。因此，近年来，数据驱动的机器人误差预测方法得到许多学者的关注。这类方法不需要建立运动学参数模型，而是将机器人系统视为一个“黑匣子”，借助外部测量工具直接测量机器人定位误差，然后采用神经网络等智能算法建立机器人构型与末端误差之间的映射关系，通过这种映射关系来估算末端点的误差进而实现补偿[11]。
Nguyen等人[12,13]指出由于非几何误差源(如连杆挠度误差、关节柔度误差、齿轮齿隙等)很难或不可能准确完整地建模，因此采用人工神经网络(ANN)对这些难以建模的误差进行补偿，并利用扩展卡尔曼滤波(EKF)算法对机器人各个关节的几何参数进行识别。将基于模型的EKF机器人几何误差识别与基于神经网络的补偿技术相结合，可以有效地解决所有机器人误差源的校正问题。王龙飞等人[14]首先通过空间网格采样方法证明机器人绝对定位误差沿不同坐标系方向存在一定的变化规律，然后建立基于极限学习机(ELM)算法的机器人定位误差预测模型，用于钻孔精度补偿。Li等人[15]提出了一种基于遗传粒子群算法优化神经网络的机器人定位误差预测方法，并利用预测误差对机器人末端位置进行补偿，进而提升机器人机加工精度。周炜等人[16]指出机器人末端相邻两点的定位精度之间存在内在关系，这种特性称为定位误差相似性。利用误差相似性，文献[17]提出一种基于深度置信网络的工业机器人位姿误差的预测方法，建立了机器人末端位姿坐标与位姿误差的映射模型。通过结合离线前馈补偿方法，实现机器人绝对定位精度的提升。
可见，现有研究一般是将机器人的末端位置和姿态作为输入，建立其与定位误差之间的映射关系，从而预测机器人末端定位误差。但是，由于6自由度机器人在同一末端位置和姿态时，会对应多个机器人的关节位姿组合，不同关节位姿组合下的末端定位误差存在较大区别。因此，使用机器人关节空间下的机器人构型作为输入，更能反映机器人定位误差的分布规律。另外，关节构型之间的时间和空间关系与末端定位误差存在较强的相关性，若能将数据之间的相对时空关系应用于机器人定位误差的预测中，将提高机器人定位误差预测的准确性。再者，对于机器人切削加工的误差预测及补偿，现有的方法大多只考虑了机器人末端位置定位误差，而忽略了机器人末端的姿态定位误差，使得误差补偿的效果不佳。
本文提出一种新的机器人定位误差预测及补偿方法，首先通过构建时-空混合的图卷积神经网络，建立机器人关节空间下6维关节坐标与笛卡儿坐标系下机器人末端6维位姿误差之间的映射关系；然后，分析机器人末端位置与姿态误差对刀具中心点作业误差的影响，并将机器人定位误差补偿问题转化为带约束下的高维寻优问题，利用遗传算法进行误差补偿；最后，通过拉丁超立方抽样方法获得训练集，构建机器人定位误差预测网络，并通过测试集验证了定位误差预测的准确性以及补偿的效果。
2. 基于时空混合图卷积网络的机器人位姿误差预测
机器人在运动过程中，末端位姿以及构型空间下的关节坐标信息与时域和空间域相关，对于机器人位姿误差的预测具有重要作用。其中，时域相关信息为不同抽样点之间的运动顺序关系，而空间域依赖信息为关节坐标信息之间的非欧氏距离。因此，本文提出了时空混合图网络，首先设计图关系编码模块提取多维位姿信息的隐藏相关特征。然后，设计时空混合特征解码模块，其中采用图傅里叶变换过程提取时域特征信息，采用离散傅里叶变换过程提取空间域特征信息。时空混合图卷积网络的网络结构如图1所示。
2.1 图关系编码模块
时空混合图卷积网络中，图关系编码模块将机器人构型空间下的6个关节角度作为图结构数据进行输入，并通过Query-Key机制，构造图权重信息矩阵，以表示不同抽样点之间的图关系。机器人关节随着末端运动的变化，需要获取关节坐标随时间变化的关系特征。因此，假设输入关节坐标的几何位置为
X∈RN×T ，其中N 为机器人末端位置采集到的样本点数；T 为各采集样本时间点机器人关节空间的维度。X 作为图关系编码模块的输入端，输入到递归网络的LSTM层[18]，计算几何位姿随着观测点时间序列的隐藏状态变量H 。在图关系编码模块中，受到Transformer模型的灵感[19]的Query-Key机制，用来跟踪当前观测点与前一时刻观测点的相关性。因此，设计了两分支的Query分支和Key分支权重WQ 和WK 。图关系编码模块的图权重信息矩阵W 可设计为全连接网络层结构形式，实现机器人构型与末端位姿的编码，可由隐藏状态变量H ，分支权重WQ ,WK 计算得到Q=HWQ (1) K=HWK (2) W=Softmax(QKT) (3) 其中，
Q 和K 分别表示Query和Key分支网络的激励值。根据式(3)，图权重信息矩阵W 可由Query和Key分支网络的激励值经过Softmax激励函数计算得到。2.2 时空混合特征解码模块
由于出色的隐空间特征学习能力，时空混合特征解码模块采用了图谱卷积操作[20]作为基本计算单元，针对图权重信息矩阵
W 进行建模。在时空混合特征解码模块中，首先采用图傅里叶变换过程提取图权重信息矩阵W 中的空间域特征信息。图傅里叶变换采用正则化的图拉普拉斯的特征向量作为基元，映射输入图信息到正交空间中L=IN−D−12WD−12 (4) 其中，
L ,IN 和D 代表拉普拉斯矩阵、单位矩阵和对角矩阵。对角矩阵可以表示为Dii=N∑j=1Wij (5) 针对拉普拉斯矩阵进行特征值分解，
L=UΛUT ，其中U 和Λ 分别代表对角矩阵D 的特征向量和对角矩阵。在图权重信息矩阵W 中，单通道的机器人关节信息对于每个图节点变成了线性独立关系。此外，在图傅里叶变换的输出端，设计时域特征提取Block，目的是转化各关节序列的时序信息到频率特征。在时域特征提取Block中，首先基于三角函数作为基底，采用离散傅里叶变换过程，提取不同时间戳内关节移动内部频率信息；针对每一通道的关节频率数据，在执行离散傅里叶逆变换过程重新转化为时域信息之前，引入1D卷积层和GLU层提取频率信息特征；值得注意的是，GLU层为门限线性层，在卷积层中引入门限机制。最后，时域特征提取Block的输出端应用图卷积操作，执行图傅里叶逆变换。
最后，采用了两个分支的全连接层网络计算偏移估计输出
ˆY 和回溯输出ˆX 。因此，时空混合图卷积网络的损失函数可以设计为回溯输出和预测输出的差异W=T∑t=0‖ (6) 其中，式(6)的第1项代表预测损失，第2项代表回溯损失。其中在回溯端，采用了循环策略的形式，
{{\boldsymbol{\hat X}}_t} 被前t - 1 ,t - 2 , ···,1 时刻的回溯损失叠加。通过应用循环策略，进而计算机器人末端位姿偏移。3. 机器人作业误差补偿
3.1 机器人位姿误差分析
在机器人操作中，机器人的末端一般需要安装末端执行器，进而执行各种不同的任务。在任务规划中，一般会将工具坐标系指定在末端执行器上，其称为工具中心点(TCP)。而机器人操作过程中的位姿误差，即为工具坐标系沿着规划的轨迹运动时，TCP点与期望位置及姿态的偏差值。由于工具坐标系与机器人末端坐标系的偏移关系，TCP的位置误差会同时受到机器人末端的线位移误差和角位移误差的影响[21]。假设机器人末端执行器不产生额外的误差，机器人末端位置与姿态误差导致末端执行器产生偏差，从而导致TCP点产生偏差，如图2所示。刀具中心点位置和姿态偏差为
\quad\qquad {{\boldsymbol{\varDelta }}_{{\text{tran}}}} = {{\boldsymbol{\delta }}_{{\text{tran}}}} + ( - {{\boldsymbol{\hat v}}_{\text{t}}}){{\boldsymbol{\delta }}_{{\text{rot}}}} (7) \quad\qquad {{\boldsymbol{\varDelta }}_{{\text{rot}}}} = {{\boldsymbol{\delta }}_{{\text{rot}}}} (8) 其中，
{{\mathbf{\delta }}_{{\text{tran}}}} = [ {{\delta _{\text{x}}}}\;\; {{\delta _{\text{y}}}}\;\;{{\delta _{\text{z}}}} ] 为机器人末端的线位移误差，{{\boldsymbol{\delta }}_{{\text{rot}}}} = [ {{\delta _{\text{a}}}}\;\; {{\delta _{\text{b}}}}\;\;{{\delta _{\text{c}}}}] 为机器人末端坐标系{E}下的角位移误差，{{\boldsymbol{v}}_{\text{t}}} = {[{v_{{\text{tx}}}},{v_{{\text{ty}}}},{v_{{\text{tz}}}}]^{\text{T}}} 表示TCP点处工具坐标系与机器人末端法兰中心的相对位置矢量。这个矢量是在坐标系{E}下定义的，在加工过程中是固定不变的。而{{\boldsymbol{\hat v}}_{\text{t}}} 是{{\boldsymbol{v}}_{\text{t}}} 的反对称矩阵，有{{\boldsymbol{\hat v}}_{\text{t}}} = \left[ {\begin{array}{*{20}{c}} 0&{ - {v_{{\text{tz}}}}}&{{v_{{\text{ty}}}}} \\ {{v_{{\text{tz}}}}}&0&{ - {v_{{\text{tx}}}}} \\ { - {v_{{\text{ty}}}}}&{{v_{{\text{tx}}}}}&0 \end{array}} \right] (9) 可见，当机器人安装末端执行器的长度越大时，末端位姿误差对机器人作业的位置精度影响越大，因此，需要对机器人位置和姿态同时进行补偿，以获得更高的作业精度。
3.2 机器人定位误差补偿方法
一般误差补偿的流程包括：当前位置的误差预测、根据误差大小和方向进行位置补偿，由于位置补偿后会产生新的误差，单次补偿后往往会导致新的误差，进而导致误差补偿效果不佳，如图3所示。针对这样的问题，一般需要多次迭代计算获得满足要求的结果。但是，在本文第2节构建的机器人位姿误差模型中，输入参数为机器人的关节坐标，在进行TCP位置调整时，需要经过机器人逆运动学解算，导致多次迭代时计算时间长、效率低的问题。
对此，本节基于机器人位姿误差预测模型，将补偿问题转换为优化问题来解决，进而减少机器人逆运动学解算的次数，具体流程如下。首先根据理想的末端位姿，通过逆解获得理想的机器人构型；然后，在设定范围内进行寻优，并根据第2节的机器人位姿误差预测模型，计算出预测机器人位姿；然后，根据预测情况，判断当前关节坐标是否达到位姿精度要求。对此，构造优化目标函数为
\left. \begin{aligned} & \min {{\boldsymbol{\varDelta }}_{{\text{tran}}}}({{\boldsymbol{\theta }}_i}) \hfill \\ & {\text{s}}{\text{.t}}{\text{.}}{{\boldsymbol{\theta }}_{i,{\text{e}}}} = {f_{{\text{ik}}}}^{ - 1}({\boldsymbol{p}}_{\text{w}}^i) \hfill \\ & {{\boldsymbol{\theta }}_{i{\text{,e}}}} - \delta \le {{\boldsymbol{\theta }}_i} \le {{\boldsymbol{\theta }}_{i,{\text{e}}}} + \delta \hfill \\ & {{\boldsymbol{\theta }}_{\min }} \le {{\boldsymbol{\theta }}_i} \le {{\boldsymbol{\theta }}_{\max }} \end{aligned} \right\} (10) 其中，
{\boldsymbol{\theta }} 为机器人的关节角度，即构型空间下的坐标信息；{\boldsymbol{p}} 为笛卡儿空间下的末端坐标，{f_{{\text{ik}}}} 为机器人逆解，只需要运算1次，即可获得理想的关节角度信息；然后关节角度在理想值附近一定的范围内，并满足机器人关节限位。在本文的问题中，根据误差值大小，寻优范围为理想关节坐标的±5°，寻优算法采用遗传算法，直接运用Matlab软件中的工具箱进行。在寻优迭代的过程中，只需要执行机器人的正运动学计算，避免了频繁逆解造成的效率下降。4. 仿真验证与分析
4.1 实验平台
在本文的定位精度测试实验中，测量对象为KUKA公司的KR210 R2700工业机器人，如图4所示。而测量系统采用了美国精密工程公司(API)的Radian型号激光跟踪仪以及安装在机器人末端执行器上的3个固定靶标作为外部测量工具，还包括数据采集器、数据采集和分析软件。3个靶标相对机器人末端坐标系的位置已经通过激光跟踪仪提前测量。通过对3个靶标位置的测量，可以同时获取机器人末端的位置与姿态。
4.2 基于拉丁超立方采样的样本获取
在神经网络的训练中，训练样本的获取是保证模型预测精度最关键的因素之一。在本文中，误差预测模型的输入参数为机器人的关节角度，输出参数为机器人的位置与姿态定位误差。由于本文采用激光跟踪仪对机器人定位误差进行测量，为了保证测量精度，需要保证所有被测点始终在跟踪仪的视野范围内。因此，此处采用拉丁超立方抽样(Latin Hypercube Sampling, LHS)方法[22]在笛卡儿空间中采集训练样本。LHS法基于分层随机的思想，其一般步骤为：(1)设变量维度为n，将每个维度变量按其变化范围，等分为m个子区间，并在子区间内随机选取一个值，从而每个维度变量得到m个值；(2)将各个维度变量的m个值随机互相组合，形成m个维度为m的向量，作为抽样样本。LHS法能够保证每一个变量在其范围内均匀全覆盖，避免了传统的随机抽样方法中数据过度聚集的问题。如图5所示，我们选取了机器人工作空间中尽量大的立方体区域作为抽样空间，尺寸为800 mm×1200 mm×1000 mm，而机器人末端姿态角的范围为[–15°, 15°]。通过LHS法进行6维的抽样，抽样数量为2000，抽样的结果如图6(a)和图6(b)所示，机器人末端位置与末端姿态的组合即为抽样点的位姿。另外，为了测量过程的高效性，抽样点的遍历可以看作旅行售货商问题(TSP)。本文根据抽样点的欧氏距离构造相似性矩阵，并通过LKH算法[23]进行求解，以减少测量过程中机器人频繁变化造成的时间浪费。
4.3 模型训练及验证
基于2000个抽样数据样本，其中1800个样本用于训练，200个样本用作测试验证。图7(a)展示了时空混合图卷积网络训练和验证过程，其中蓝色曲线代表时空混合图卷积网络的训练过程，橙色曲线代表时空混合图卷积网络的验证过程。时空混合图卷积网络的训练损失值从0.9下降到0.05；空间图卷积网络的验证损失值从0.38下降到0.05。最终，随着迭代次数增加到30，训练损失值和验证损失损失值均收敛到接近值。由图7可以看出，时空混合图卷积网络无论是在训练集还是测试集上，均取得了显著性的收敛信息。
图8(a)—图8(f)分别表示时空混合图卷积网络在X轴、Y轴、Z轴、
\alpha 角、\beta 角、\chi 角方面，实际误差值和补偿后误差拟合度的表现情况对比。其中蓝色点代表实际误差值，红色直线代表将补偿后误差进行线性回归后的可视化图像。R2代表拟合度，作为衡量实际误差和补偿误差的拟合程度，被广泛使用[24,25]。由回归平方和与总离差平方和之比值决定。从图8可以看出，时空混合图卷积网络在X轴、Y轴、Z轴、α角、β角、γ角的拟合度分别达到了0.928，0.932，0.973，0.978，0.999，0.962。另外，为了体现上述网络的效果，构建了7层卷积网络作为对比方法。7层卷积网络由2层卷积层、2层池化层和3层全连接层构成。卷积层采用了1维卷积核，池化层采用了1维最大池化层。7层卷积网络的网络配置如表1所示。
表 1 7层卷积网络的网络配置层数 1 2 3 4 5 6 7 网络配置 Conv1D
(30, 3, relu)MaxPooling1D (2) Conv1D (1, 3, ReLU) MaxPooling1D (2) Dense
(50)Dense
(50)Dense
(6)其中卷积网络的配置Conv1D (. , . , .)分别表示卷积模板数量、卷积核尺寸和激励函数；池化层的配置Pooling1D ( . )表示池化步长；全连接层的配置Dense ( . )表示全连接层神经元数量。
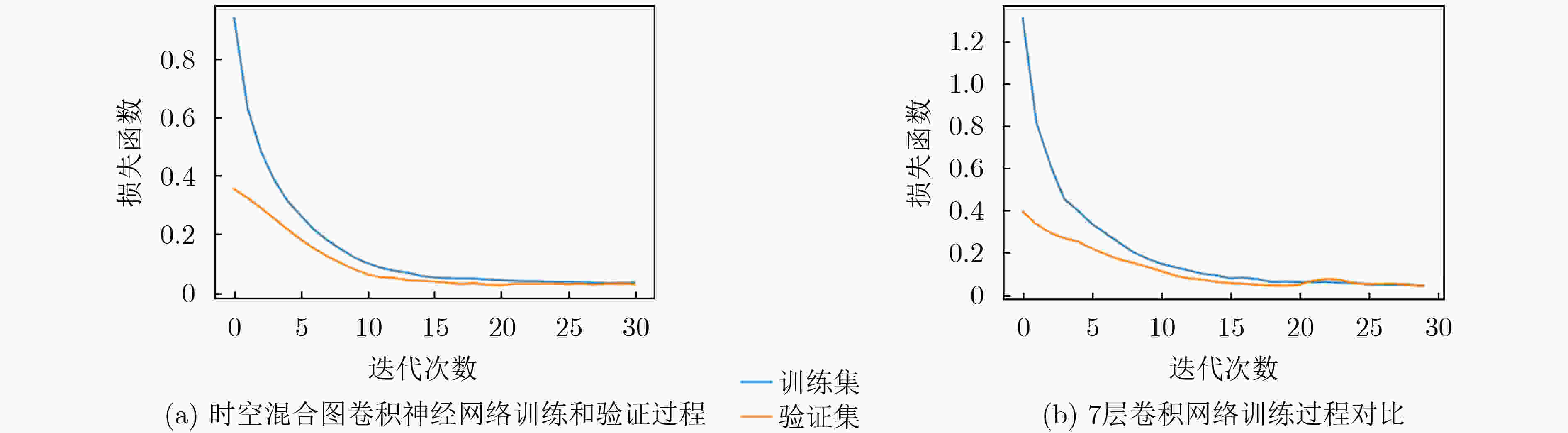
首先，将时空混合图卷积神经网络和7层卷积神经网络在训练中的损失函数进行了对比，如图7(a)，图7(b)之间的对比可见，时空图卷积神经网络在迭代到第10次时实现稳定收敛；而7层卷积网络则用了20次迭代。由此看出，时空图卷积神经网络相比于7层卷积网络，计算效率更高。然后，如表2所示为两个模型在误差预测性能中的对比。可以看出，对于测试数据，本文网络中机器人的位姿误差预测偏差为0.0114；而7层卷积网络的为0.0526。可见，时空图卷积神经网络的预测准确率更高。
表 2 7层卷积网络的网络配置模型 误差 时空图卷积网络 0.0114 7层卷积网络 0.0526 4.4 机器人定位误差补偿效果验证
根据机器人位姿误差预测模型，计算出测试点的误差值，并进行误差补偿。补偿后的机器人位姿重新输出到机器人控制器中，并利用激光跟踪仪对其位置和姿态的误差进行测量，与理想位姿进行对比，即可获得补偿后的机器人位姿误差。误差补偿后，3个轴向的线位移误差以及基坐标系下角位移误差如图9所示。可以看出，机器人的位姿误差均得到较好的抑制，总位置误差从最大2.75 mm降低到了0.56 mm，姿态误差从最大0.39°，降低到了0.18°，分别降低了79.6%及53.8%。试验结果表明，本文的误差预测及补偿方法能够有效提高机器人的位置和姿态定位精度。
5. 结论
针对工业机器人定位精度低的问题，本文首先构建了基于图关系编码模块和时空混合特征解码模块的图卷积神经网络，建立了机器人关节空间关节坐标与笛卡儿空间位姿坐标的映射关系，实现了机器人位姿误差的预测；然后，在此基础上，分析了机器人构型误差对机器人末端执行器定位精度影响情况，进而实现机器人定位误差补偿，提高机器人定位精度；在实验验证中，在机器人定位精度测量系统搭建的基础上，建立了基于拉丁超立方抽样方法的数据采集方法。通过对机器人位置与姿态误差预测及补偿效果的验证，证明了本文算法的有效性。
-
表 1 7层卷积网络的网络配置
层数 1 2 3 4 5 6 7 网络配置 Conv1D
(30, 3, relu)MaxPooling1D (2) Conv1D (1, 3, ReLU) MaxPooling1D (2) Dense
(50)Dense
(50)Dense
(6)
下载: 导出CSV
-
[1] CHEN Yubao. Integrated and intelligent manufacturing: Perspectives and enablers[J]. Engineering, 2017, 3(5): 588–595. doi: 10.1016/J.ENG.2017.04.009 [2] ZHU Zerun, TANG Xiaowei, CHEN Chen, et al. High precision and efficiency robotic milling of complex parts: Challenges, approaches and trends[J]. Chinese Journal of Aeronautics, 2022, 35(2): 22–46. doi: 10.1016/j.cja.2020.12.030 [3] KIM S H, NAM E, HA T I, et al. Robotic machining: A review of recent progress[J]. International Journal of Precision Engineering and Manufacturing, 2019, 20(9): 1629–1642. doi: 10.1007/s12541-019-00187-w [4] GUO Yingjie, DONG Huiyue, WANG Guifeng, et al. Vibration analysis and suppression in robotic boring process[J]. International Journal of Machine Tools and Manufacture, 2016, 101: 102–110. doi: 10.1016/j.ijmachtools.2015.11.011 [5] YE Congcong, YANG Jixiang, ZHAO Huan, et al. Task-dependent workpiece placement optimization for minimizing contour errors induced by the low posture-dependent stiffness of robotic milling[J]. International Journal of Mechanical Sciences, 2021, 205: 106601. doi: 10.1016/j.ijmecsci.2021.106601 [6] NUBIOLA A and BONEV I A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(1): 236–245. doi: 10.1016/j.rcim.2012.06.004 [7] HU J, HUA F, and TIAN W. Robot positioning error compensation method based on deep neural network[J]. Journal of Physis Coference Series, 2020, 1487: 012045. [8] YANG Xiangdong, WU Liao, LI Jinquan, et al. A minimal kinematic model for serial robot calibration using POE formula[J]. Robotics and Computer-Integrated Manufacturing, 2014, 30(3): 326–334. doi: 10.1016/j.rcim.2013.11.002 [9] RENDERS J M, ROSSIGNOL E, BECQUET M, et al. Kinematic calibration and geometrical parameter identification for robots[J]. IEEE Transactions on Robotics and Automation, 1991, 7(6): 721–732. doi: 10.1109/70.105381 [10] MA Le, BAZZOLI P, SAMMONS P M, et al. Modeling and calibration of high-order joint-dependent kinematic errors for industrial robots[J]. Robotics and Computer-Integrated Manufacturing, 2018, 50: 153–167. doi: 10.1016/j.rcim.2017.09.006 [11] ALICI G and SHIRINZADEH B. A systematic technique to estimate positioning errors for robot accuracy improvement using laser interferometry based sensing[J]. Mechanism and Machine Theory, 2005, 40(8): 879–906. doi: 10.1016/j.mechmachtheory.2004.12.012 [12] NGUYEN H N, ZHOU Jian, and KANG H J. A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network[J]. Neurocomputing, 2015, 151: 996–1005. doi: 10.1016/j.neucom.2014.03.085 [13] NGUYEN H N, LE P N, and KANG H J. A new calibration method for enhancing robot position accuracy by combining a robot model–based identification approach and an artificial neural network–based error compensation technique[J]. Advances in Mechanical Engineering, 2019, 11(1): 1–11. doi: 10.1177/1687814018822935 [14] 王龙飞, 李旭, 张丽艳, 等. 工业机器人定位误差规律分析及基于ELM算法的精度补偿研究[J]. 机器人, 2018, 40(6): 843–851,859. doi: 10.13973/j.cnki.robot.170536WANG Longfei, LI Xu, ZHANG Liyan, et al. Analysis of the positioning error of industrial robots and accuracy compensation based on ELM algorithm[J]. Robot, 2018, 40(6): 843–851,859. doi: 10.13973/j.cnki.robot.170536 [15] LI Bo, TIAN Wei, ZHANG Chufan, et al. Positioning error compensation of an industrial robot using neural networks and experimental study[J]. Chinese Journal of Aeronautics, 2022, 35(2): 346–360. doi: 10.1016/j.cja.2021.03.027 [16] 周炜, 廖文和, 田威. 基于空间插值的工业机器人精度补偿方法理论与试验[J]. 机械工程学报, 2013, 49(3): 42–48. doi: 10.3901/JME.2013.03.042ZHOU Wei, LIAO Wenhe, and TIAN Wei. Theory and experiment of industrial robot accuracy compensation method based on spatial interpolation[J]. Journal of Mechanical Engineering, 2013, 49(3): 42–48. doi: 10.3901/JME.2013.03.042 [17] WANG Wei, TIAN Wei, LIAO Wenhe, et al. Error compensation of industrial robot based on deep belief network and error similarity[J]. Robotics and Computer-Integrated Manufacturing, 2022, 73: 102220. doi: 10.1016/j.rcim.2021.102220 [18] HU Ruihan, HUANG Qijun, WANG Hao, et al. Monitor-based spiking recurrent network for the representation of complex dynamic patterns[J]. International Journal of Neural Systems, 2019, 29(8): 1950006. doi: 10.1142/S0129065719500060 [19] SUN Peize, CAO Jinkun, JIANG Yi, et al. TransTrack: Multiple object tracking with transformer[J]. arXiv preprint arXiv: 2012.15460, 2020. [20] SHANG Chao, LIU Qinqing, TONG Qianqian, et al. Multi-view spectral graph convolution with consistent edge attention for molecular modeling[J]. Neurocomputing, 2021, 445: 12–25. doi: 10.1016/J.NEUCOM.2021.02.025 [21] LIAO Zhaoyang, WANG Qinghui, XIE Hailong, et al. Optimization of robot posture and workpiece setup in robotic milling with stiffness threshold[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(1): 582–593. doi: 10.1109/TMECH.2021.3068599 [22] VAN DAM E R, HUSSLAGE B, DEN HERTOG D, et al. Maximin Latin hypercube designs in two dimensions[J]. Operations Research, 2007, 55(1): 158–169. doi: 10.1287/opre.1060.0317 [23] HELSGAUN K. General k-opt submoves for the Lin–Kernighan TSP heuristic[J]. Mathematical Programming Computation, 2009, 1(2): 119–163. doi: 10.1007/s12532-009-0004-6 [24] HAYES T. R-squared change in structural equation models with latent variables and missing data[J]. Behavior Research Methods, 2021, 53(5): 2127–2157. doi: 10.3758/S13428-020-01532-Y [25] MISHRA V N, KUMAR V, PRASAD R, et al. Geographically weighted method integrated with logistic regression for analyzing spatially varying accuracy measures of remote sensing image classification[J]. Journal of the Indian Society of Remote Sensing, 2021, 49(5): 1189–1199. doi: 10.1007/s12524-020-01286-2 期刊类型引用(6)
1. 肖蛰水，陈发，方坤升，王巍，黄海宁. 水下体域网系统架构及关键技术. 水下无人系统学报. 2022(06): 720-725 . 
百度学术2. 孙彦赞，范卫蓉，张舜卿，王涛，吴雅婷. 基于图着色的密集D2D网络资源分配算法. 计算机工程. 2019(02): 26-31 . 百度学术3. 赖增桂，蔡雪梅，李默嘉. 基于时隙泛洪的无路由移动无线自组网协议及其扩展方法. 通信技术. 2018(03): 605-610 . 百度学术4. 柳扬，杨银堂，李迪，石佐辰. 一种无线体域网发射机体偏置线性化技术. 电子与信息学报. 2017(02): 499-503 . 
本站查看5. 房卫东，张武雄，胡明明，陈伟，杨旸. 基于改进LDPC码的短距离跳频无线通信系统. 通信学报. 2017(12): 34-47 . 百度学术6. 李建辉，刘畅，王彩申，王强强. 基于WBAN的多参数健康监护系统研究与设计. 现代电子技术. 2017(22): 149-151 . 百度学术其他类型引用(1)
-
下载:
百度学术
计量
- 文章访问数: 1158
- HTML全文浏览量: 697
- PDF下载量: 133
- 被引次数: 7
下载:
