Flexible Integrated Scheduling Algorithm Based on Reverse Order Layer Priority
-
摘要: 针对以往柔性综合调度算法均考虑正向调度，导致需要考虑目标工序的多紧前工序约束条件，难以合理安排相关工序进而影响产品完工时间的问题，该文提出一种基于逆序层优先的柔性综合调度算法。首先，提出逆序层优先策略，将各工序分配至逆序层待调度工序集；其次，提出动态拟长路径策略，确定各逆序层待调度工序集中工序的调度顺序；然后，分别提出设备选择策略和设备抢占策略以确定目标工序的加工设备以及加工时间；最后，提出基于完工时间翻转的调度方案转换策略，将逆序调度方案转换为正序调度方案。实例表明，和已有主流算法相比，该算法在不提高算法复杂度的前提下能够缩短产品完工时间。Abstract: In view of the previous flexible integrated scheduling algorithms that consider forward scheduling, so that it is necessary to consider the multiply predecessors’ constraints of the target operation, which makes it difficult to arrange rationally the relevant operations and affect the product completion time. A flexible integrated scheduling algorithm based on reverse order layer priority is proposed. Firstly, a reverse-order layer priority strategy is proposed, and each operation is allocated to the set of operations to be scheduled in the reverse-order layer; Secondly, a dynamic pseudo-long path strategy is proposed to determine the scheduling sequence of the centralized operation of each reverse-order layer to be scheduled; Then, the equipment selection strategy and the equipment preemption strategy are proposed to determine the processing equipment and processing time of the target operation. Finally, a scheduling plan conversion strategy based on the completion time flip is proposed, which converts the reverse order scheduling scheme into a positive order scheduling scheme. The example shows that compared with the existing mainstream algorithms, this algorithm can shorten the product completion time without increasing the complexity of the algorithm.
-
[1] GMYS J, MEZMAZ M, MELAB N, et al. A computationally efficient Branch-and-Bound algorithm for the permutation flow-shop scheduling problem[J]. European Journal of Operational Research, 2020, 284(3): 814–833. doi: 10.1016/j.ejor.2020.01.039 [2] REN Weibo, WEN Jingqian, YAN Yan, et al. Multi-objective optimisation for energy-aware flexible job-shop scheduling problem with assembly operations[J]. International Journal of Production Research, 2021, 59(23): 7216–7231. doi: 10.1080/00207543.2020.1836421 [3] ZOU Yunqing, WANG Dujuan, LIN W C, et al. Two-stage three-machine assembly scheduling problem with sum-of-processing-times-based learning effect[J]. Soft Computing, 2020, 24(7): 5445–5462. doi: 10.1007/s00500-019-04301-y [4] WU C C, GUPTA J N D, CHENG S R, et al. Robust scheduling for a two-stage assembly shop with scenario-dependent processing times[J]. International Journal of Production Research, 2021, 59(17): 5372–5387. doi: 10.1080/00207543.2020.1778208 [5] TIRKOLAEE E B, GOLI A, and WEBER G W. Fuzzy mathematical programming and self-adaptive artificial fish swarm algorithm for just-in-time energy-aware flow shop scheduling problem with outsourcing option[J]. IEEE Transactions on Fuzzy Systems, 2020, 28(11): 2772–2783. doi: 10.1109/TFUZZ.2020.2998174 [6] OUKIL A and EL-BOURI A. Ranking dispatching rules in multi-objective dynamic flow shop scheduling: A multi-faceted perspective[J]. International Journal of Production Research, 2021, 59(2): 388–411. doi: 10.1080/00207543.2019.1696487 [7] GAO Da, WANG Gaige, and PEDRYCZ W. Solving fuzzy job-shop scheduling problem using DE algorithm improved by a selection mechanism[J]. IEEE Transactions on Fuzzy Systems, 2020, 28(12): 3265–3275. doi: 10.1109/TFUZZ.2020.3003506 [8] AHMADIAN M M, SALEHIPOUR A, and CHENG T C E. A meta-heuristic to solve the just-in-time job-shop scheduling problem[J]. European Journal of Operational Research, 2021, 288(1): 14–29. doi: 10.1016/j.ejor.2020.04.017 [9] XIE Zhiqiang, HAO Shuzhen, YE Guangjie, et al. A new algorithm for complex product flexible scheduling with constraint between jobs[J]. Computers & Industrial Engineering, 2009, 57(3): 766–772. doi: 10.1016/j.cie.2009.02.004 [10] BIRGIN E G, FEOFILOFF P, FERNANDES C G, et al. A MILP model for an extended version of the flexible job shop problem[J]. Optimization Letters, 2014, 8(4): 1417–1431. doi: 10.1007/s11590-013-0669-7 [11] GAO Yilong, XIE Zhiqiang, and YU Xu. A hybrid algorithm for integrated scheduling problem of complex products with tree structure[J]. Multimedia Tools and Applications, 2020, 79(43): 32285–32304. doi: 10.1007/s11042-020-09477-2 [12] 谢志强, 吕妮. 存在预启动设备的综合调度算法[J]. 机械工程学报, 2021, 57(17): 217–225. doi: 10.3901/JME.2021.17.217XIE Zhiqiang and LÜ Ni. Integrated scheduling algorithm with pre-start device[J]. Journal of Mechanical Engineering, 2021, 57(17): 217–225. doi: 10.3901/JME.2021.17.217 [13] 谢志强, 邵侠, 杨静. 存在设备无关延迟约束的综合柔性调度算法[J]. 机械工程学报, 2011, 47(4): 177–185. doi: 10.3901/JME.2011.04.177XIE Zhiqiang, SHAO Xia, and YANG Jing. Algorithm for integrated flexible scheduling with device-independence deferred constraint[J]. Journal of Mechanical Engineering, 2011, 47(4): 177–185. doi: 10.3901/JME.2011.04.177 [14] 谢志强, 周含笑, 于洁, 等. 基于设备驱动的综合柔性调度冲突调解算法[J]. 北京理工大学学报, 2014, 34(11): 1150–1156. doi: 10.15918/j.tbit1001-0645.2014.11.011XIE Zhiqiang, ZHOU Hanxiao, YU Jie, et al. Conflict mediation algorithm of the integrated flexible scheduling based on device driver[J]. Transactions of Beijing Institute of Technology, 2014, 34(11): 1150–1156. doi: 10.15918/j.tbit1001-0645.2014.11.011 [15] BIRGIN E G, FERREIRA J E, and RONCONI D P. List scheduling and beam search methods for the flexible job shop scheduling problem with sequencing flexibility[J]. European Journal of Operational Research, 2015, 247(2): 421–440. doi: 10.1016/j.ejor.2015.06.023 [16] 谢志强, 桂忠艳, 杨静. 基于设备驱动和实质路径的动态并行综合柔性调度算法[J]. 机械工程学报, 2014, 50(18): 203–212. doi: 10.3901/JME.2014.18.203XIE Zhiqiang, GUI Zhongyan, and YANG Jing. Dynamic parallel integrated flexible scheduling algorithm based on device driver and essential path[J]. Journal of Mechanical Engineering, 2014, 50(18): 203–212. doi: 10.3901/JME.2014.18.203 [17] 赵诗奎, 韩青, 王桂从. 基于虚拟零部件级别分区编码的产品综合调度算法[J]. 计算机集成制造系统, 2015, 21(9): 2435–2445. doi: 10.13196/j.cims.2015.09.020ZHAO Shikui, HAN Qing, and WANG Guicong. Product comprehensive scheduling algorithm based on virtual component level division coding[J]. Computer Integrated Manufacturing Systems, 2015, 21(9): 2435–2445. doi: 10.13196/j.cims.2015.09.020 [18] LEI Qi, GUO Weifei, and SONG Yuchuan. Integrated scheduling algorithm based on an operation relationship matrix table for tree-structured products[J]. International Journal of Production Research, 2018, 56(16): 5437–5456. doi: 10.1080/00207543.2018.1442942 -
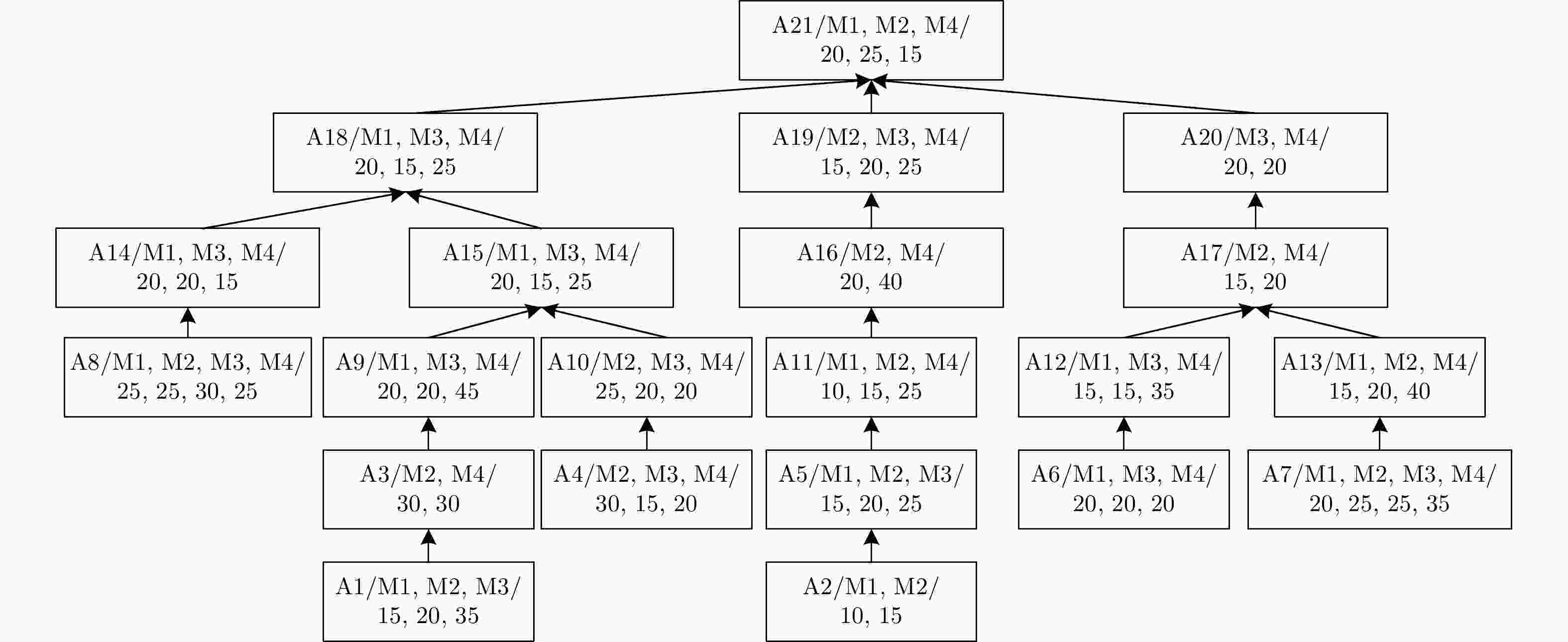
下载:
图(8)
计量
- 文章访问数: 349
- HTML全文浏览量: 178
- PDF下载量: 46
- 被引次数: 0
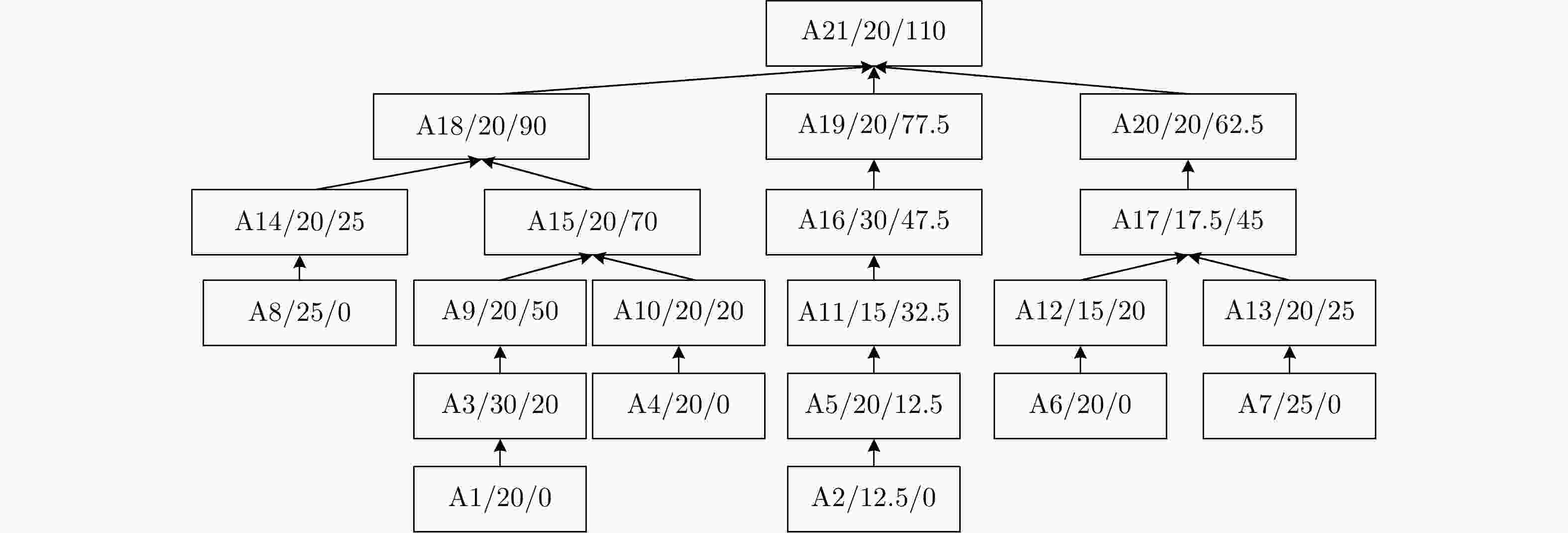
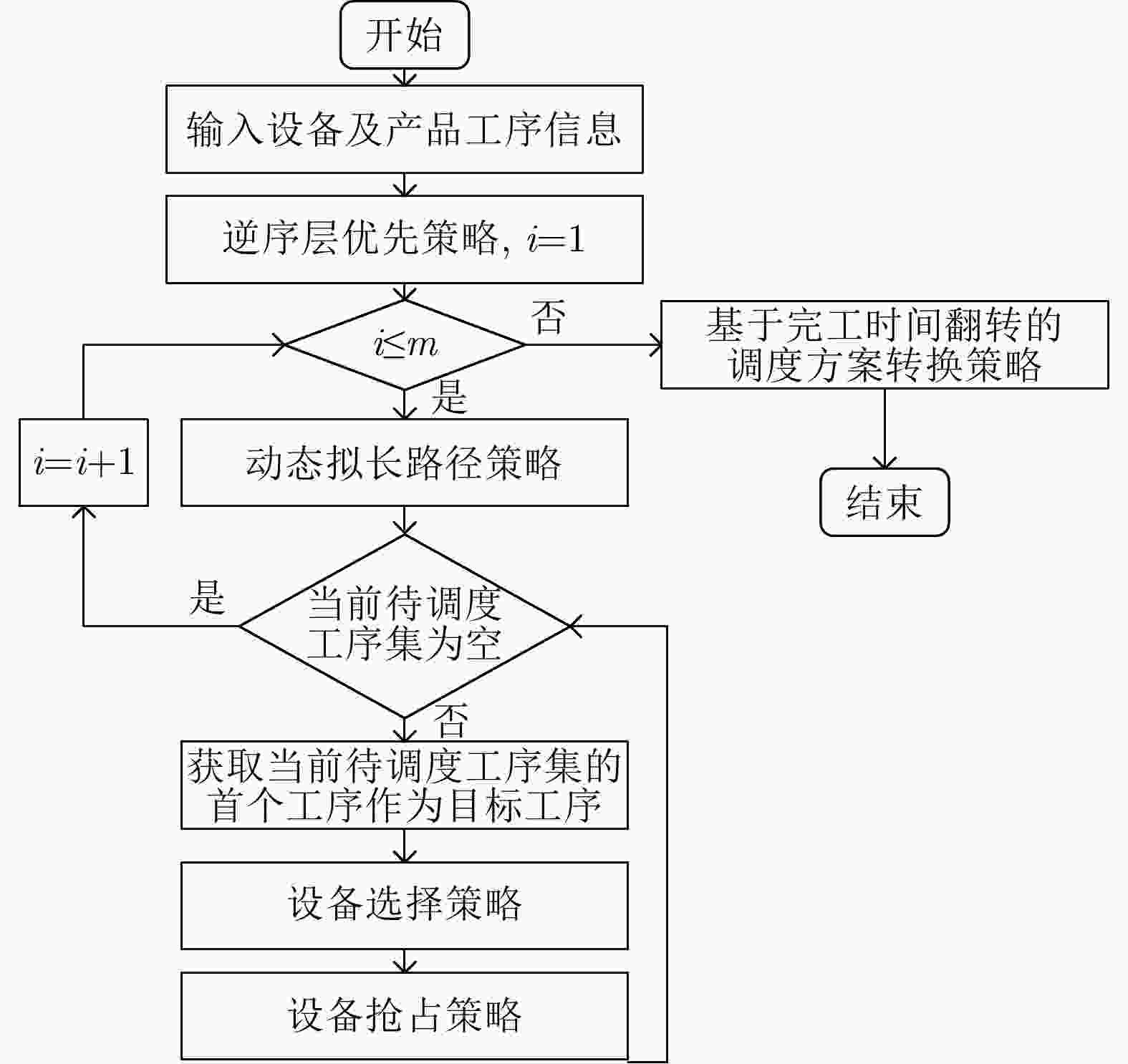
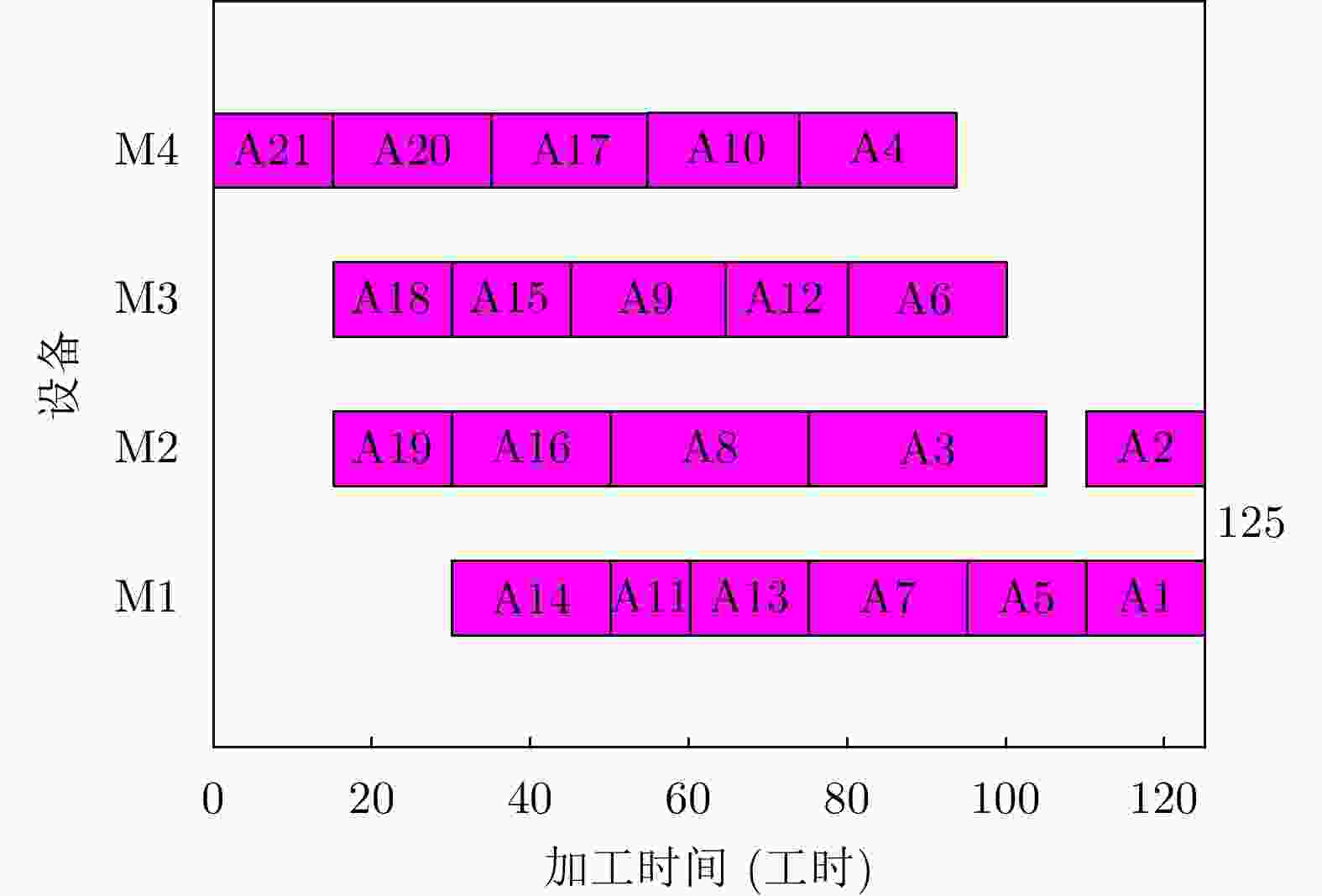
下载:
