UAV-relay Assisted Covert Communication with Finite Block-length
-
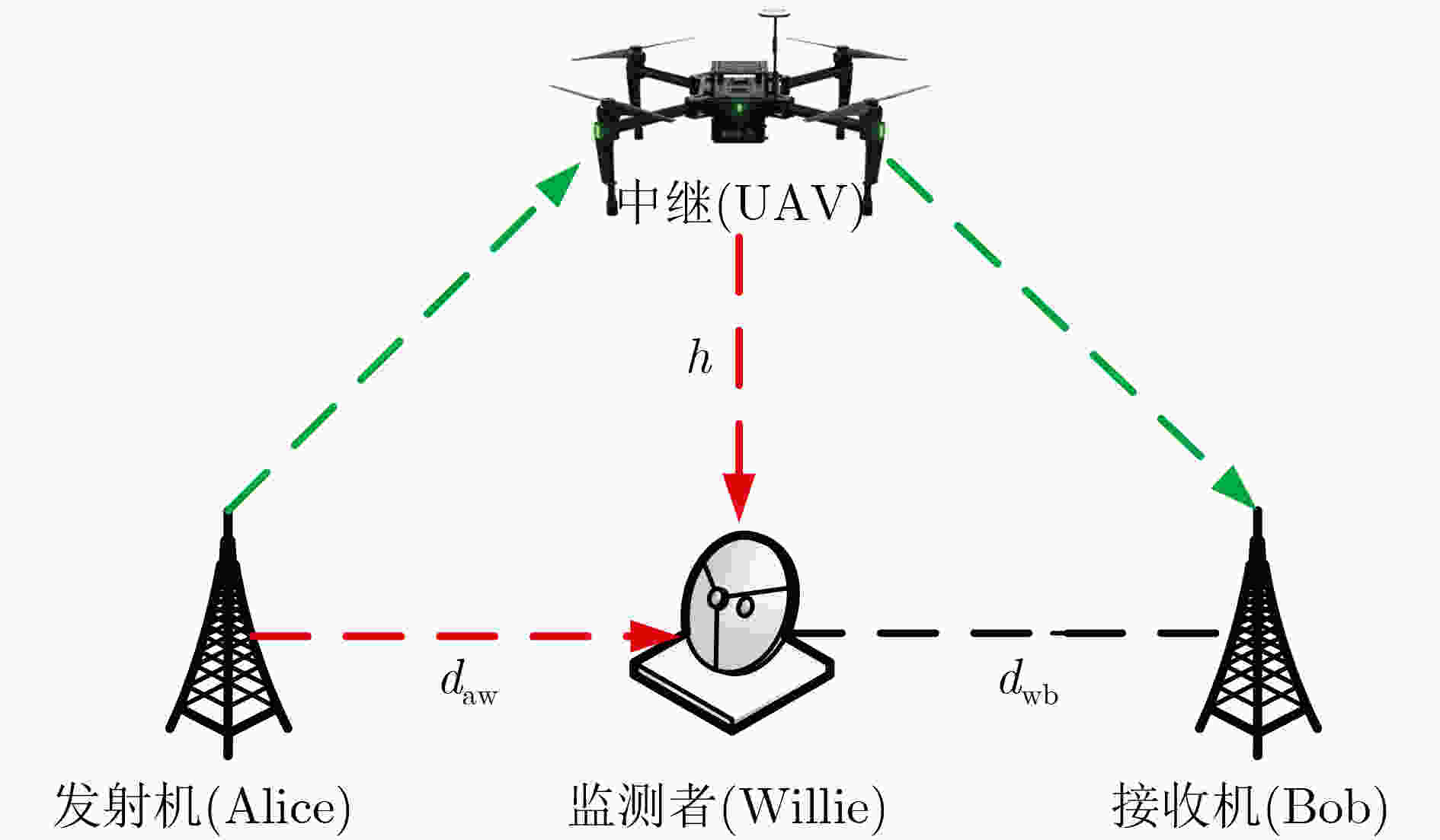
摘要: 由于中长距离的无线隐蔽通信中信号发射功率较大,容易被监测者检测到,针对此问题该文提出无人机(UAV)中继协助的有限码长隐蔽传输方案。首先,根据无人机通信的信道模型,推导从发射机经过无人机中继到合法接收机的信噪比(SNR),得到隐蔽传输中断概率及吞吐量的表达式;然后,分析监测者的检测性能, 即KL(Kullback-Leibler)散度,并将其作为隐蔽通信的约束条件;最后,在此约束的条件下,联合优化发射机和中继的发射功率以及无人机的飞行高度,从而最大化隐蔽通信的吞吐量。仿真结果验证了系统的隐蔽性能,并且通过与缺少无人机协助的传统方案对比,揭示所提出的无人机中继隐蔽传输方案可以有效地降低监测者的KL散度。Abstract: To avoid the high detection in long-distance covert communications due to the large transmission power, an Unmanned Aerial Vehicle (UAV)-relay based covert communication scheme with finite block block-length is proposed in this paper. Firstly, the Signal-to -Noise-Ratio (SNR) at the legal receiver via the UAV-relay is derived, based on which the outage probability and throughput of the covert communication link are also obtained. Secondly, the detection performance of the monitor is analyzed, i.e. KL (Kullback-Leibler) scatter, and it is used as a constraint on the covert communication. Finally, to maximize the throughput of the covert communication, the transmission power at the transmitter and the UAV-relay, as well as the flight height of UAV are jointly optimized. The simulation results verify the performance of the proposed covert communication scheme, and also show its superiority to the traditional strategies without UAVs since it greatly reduces the KL divergence at the warder.
-
Key words:
- Covert communication /
- Unmanned Aerial Vehicle (UAV) /
- Relay /
- Finite block-length
-
表 1 关于最大隐蔽吞吐量及最优发射功率算法
输入:初始化$ {D_{01}} $,$ \epsilon $,$ \delta $,$ {P}_{a}^{\mathrm{max}} $,$ {P}_{r}^{\mathrm{max}} $,$ {\gamma _w} $,$ {\gamma _b} $;给定传输速率$ R $; 输出:$ {\eta ^*} $,$ P_a^{\text{*}} $,$ P_r^{\text{*}} $。 (1)将优化问题式(17)转化为两个子优化问题式(25)、式(29); (a)根据式(16),求得$ {D_{01}} $关于$ {\gamma _w} $的1阶导数,将隐蔽性约束转化为一个等式,通过$ {D}_{01}({\gamma }_{w}^{‡})=2{\epsilon}^{2} $得到$ \gamma _w^\ddag $;
(b)通过求$ {\gamma _w} $关于$ {P_a} $的偏导,利用链式法则,得到$ {D_{01}} $关于$ {P_a} $的偏导$ \dfrac{{\partial {D_{01}}}}{{\partial {P_a}}} = \dfrac{{{\text{d}}{D_{01}}}}{{{\text{d}}{\gamma _w}}}\dfrac{{\partial {\gamma _w}}}{{\partial {P_a}}} $;
(c)通过求$ {\gamma _w} $关于$ {P_r} $的偏导,讨论${\bar \rho _{{\rm{ar}}} }\sigma _w^2$、${\bar \rho _{{\rm{aw}}} }\sigma _r^2$的关系,利用链式法则,得到$ {D_{01}} $关于$ {P_r} $的偏导$ \dfrac{{\partial {D_{01}}}}{{\partial {P_r}}} = \dfrac{{{\text{d}}{D_{01}}}}{{{\text{d}}{\gamma _w}}}\dfrac{{\partial {\gamma _w}}}{{\partial {P_r}}} $;(2)根据式(15),由$ {\gamma _w}(P_a^\ddag ) = \gamma _w^\ddag $,可以反解出$ P_a^\ddag $,通过给定$ {P_r} $,得到最优发射功率$ P_a^* = \min \{ P_a^\ddag ,P_a^{\max }\} $来求解优化问题式(25); (3)根据式(15),由$ {\gamma _w}(P_r^\ddag ) = \gamma _w^\ddag $,得到$ P_r^\ddag $; (a)当${\bar \rho _{{\rm{ar}}} }\sigma _w^2 > {\bar \rho _{{\rm{aw}}} }\sigma _r^2$时,得到最优发射功率$ P_r^* = \min \{ P_r^\ddag ,P_r^{\max }\} $求解优化问题式(29); (b)当${\bar \rho _{{\rm{ar}}} }\sigma _w^2 < {\bar \rho _{{\rm{aw}}} }\sigma _r^2$时,给定$ {P_r} = P_r^{\max } $,得到$ P_a^* = \min \{ P_a^\ddag ,P_a^{\max }\} $; (4)根据$ \eta = R(1 - \delta ) $,得到最大隐蔽吞吐量$ {\eta ^*} $; (a)根据式(11),利用${\rm{Q}}$函数,求得$ \delta $关于$ {\gamma _b} $的1阶导数; (b)由于$ \eta $与$ \delta $成反比,当$ \delta $取最小值时,得到最大的隐蔽吞吐量$ {\eta ^*} $。 -
[1] YAN Shihao, ZHOU Xiangyun, HU Jinsong, et al. Low probability of detection communication: Opportunities and challenges[J]. IEEE Wireless Communications, 2019, 26(5): 19–25. doi: 10.1109/MWC.001.1900057 [2] GOECKEL D, BASH B, GUHA S, et al. Covert communications when the warden does not know the background noise power[J]. IEEE Communications Letters, 2016, 20(2): 236–239. doi: 10.1109/LCOMM.2015.2507594 [3] ZHENG Tongxing, Wang Huiming, NG D W K, et al. Multi-antenna covert communications in random wireless networks[J]. IEEE Transactions on Wireless Communications, 2019, 18(3): 1974–1987. doi: 10.1109/TWC.2019.2900915 [4] SHAHZAD K, ZHOU Xiangyun, and YAN Shihao. Covert wireless communication in presence of a multi-antenna adversary and delay constraints[J]. IEEE Transactions on Vehicular Technology, 2019, 68(12): 12432–12436. doi: 10.1109/TVT.2019.2948608 [5] CHEN Xinying, SUN Wen, XING Chengwen, et al. Multi-antenna covert communication via full-duplex jamming against a warden with uncertain locations[J]. IEEE Transactions on Wireless Communication, 2021, 20(8): 5467–5480. doi: 10.1109/TWC.2021.3068096 [6] HU Jinsong, YAN Shihao, ZHOU Xiangyun, et al. Covert communication achieved by a greedy relay in wireless networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(7): 4766–4779. doi: 10.1109/TWC.2018.2831217 [7] SHEIKHOLESLAMI A, GHADERI M, TOWSLEY D, et al. Multi-hop routing in covert wireless networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(6): 3656–3669. doi: 10.1109/TWC.2018.2812881 [8] JIANG Xu, CHEN Xinying, TANG Jie, et al. Covert communication in UAV-assisted air-ground networks[J]. IEEE Wireless Communications, 2021, 28(4): 190–197. doi: 10.1109/MWC.001.2000454 [9] ZHOU Xiaobo, YAN Shihao, HU Jinsong, et al. Joint optimization of a UAV's trajectory and transmit power for covert communications[J]. IEEE Transactions on Signal Processing, 2019, 67(16): 4276–4290. doi: 10.1109/TSP.2019.2928949 [10] JIANG Xu, YANG Zhutian, ZHAO Nan, et al. Resource allocation and trajectory optimization for UAV-enabled multi-user covert communications[J]. IEEE Transactions on Vehicular Technology, 2021, 70(2): 1989–1994. doi: 10.1109/TVT.2021.3053936 [11] CHEN Xinying, CHANG Zheng, TANG Jie, et al. UAV-aided multi-antenna covert communication against multiple wardens[C]. The 2021 IEEE International Conference on Communications, Montreal, Canada, 2021: 1–6. [12] CHEN Xinying, ZHANG Ning, TANG Jie, et al. UAV-aided covert communication with a multi-antenna jammer[J]. IEEE Transactions on Vehicular Technology, 2021, 70(11): 11619–11631. doi: 10.1109/TVT.2021.3112121 [13] ZHOU Yi, YEOH P L, CHEN He, et al. Improving physical layer security via a UAV friendly jammer for unknown eavesdropper location[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 11280–11284. doi: 10.1109/TVT.2018.2868944 [14] ALZENAD M, EL-KEYI A, and YANIKOMEROGLU H. 3-D placement of an unmanned aerial vehicle base station for maximum coverage of users with different QoS requirements[J]. IEEE Wireless Communications Letters, 2018, 7(1): 38–41. doi: 10.1109/LWC.2017.2752161 [15] AL-HOURANI A, KANDEEPAN S, and LARDNER S. Optimal LAP altitude for maximum coverage[J]. IEEE Wireless Communications Letters, 2014, 3(6): 569–572. doi: 10.1109/LWC.2014.2342736 [16] KRIKIDIS I, THOMPSON J, MCLAUGHLIN S, et al. Amplify-and-forward with partial relay selection[J]. IEEE Communications Letters, 2008, 12(4): 235–237. doi: 10.1109/LCOMM.2008.071987 [17] SHU Feng, XU Tingzhen, HU Jinsong, et al. Delay-constrained covert communications with a full-duplex receiver[J]. IEEE Wireless Communications Letters, 2019, 8(3): 813–816. doi: 10.1109/LWC.2019.2894617 -





 下载:
下载:
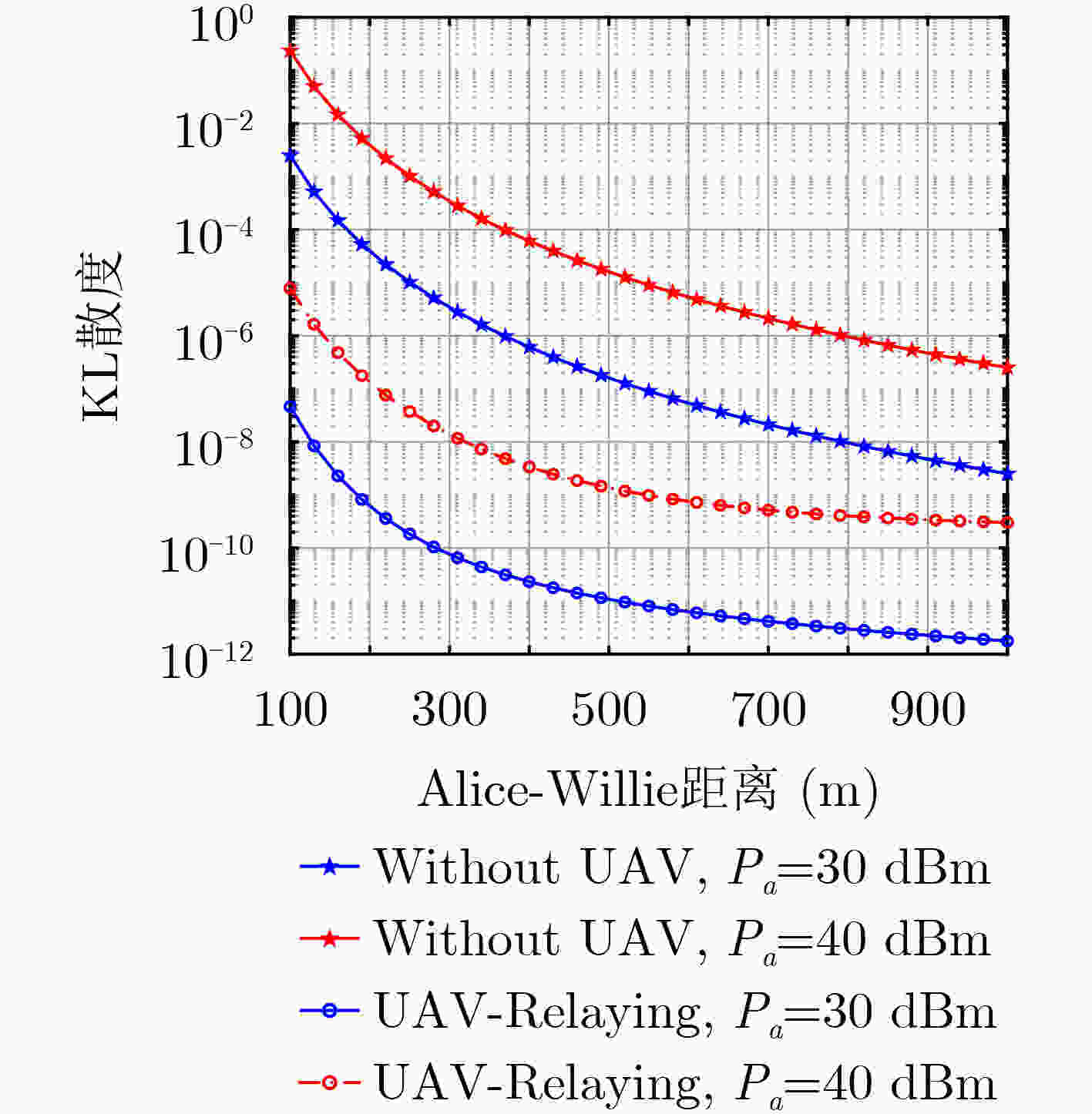


 下载:
下载:
