Outage Performance Analysis of Unmanned Aerial Vehicle Assisted Satellite Communication System with Cooperative Non-Orthogonal Multiple Access
-
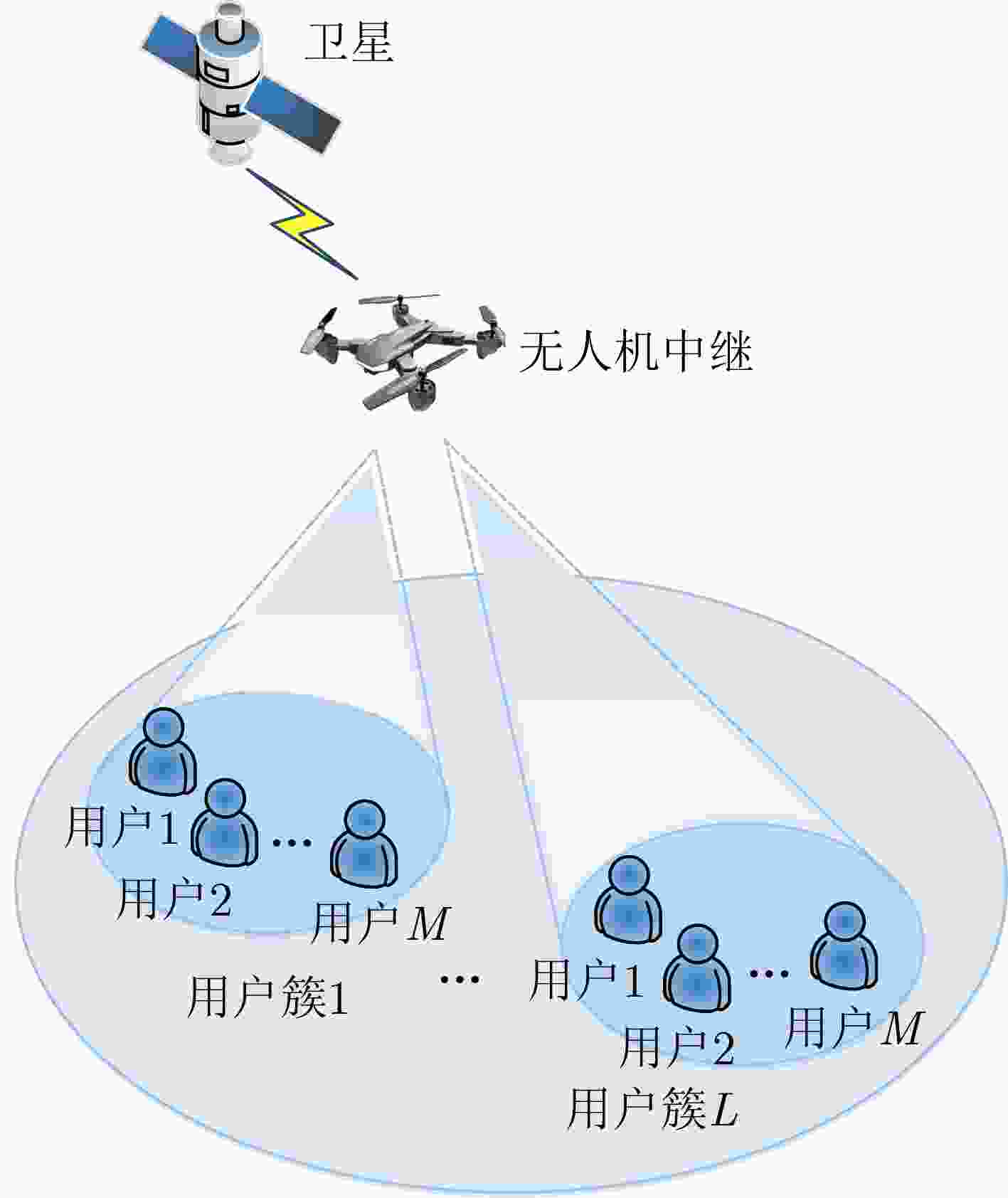
摘要: 针对无人机(UAV)辅助的卫星通信系统下行链路,该文研究了基于多天线波束成形和协作非正交多址(NOMA)技术相结合的多用户传输系统。首先,在UAV采用多天线和NOMA技术服务多个用户的情况下,基于用户平均信干噪比最大化准则,提出一种利用角度信息的波束成形方案。其次,在卫星-UAV链路服从相关阴影莱斯分布,而UAV-地面用户链路服从Nakagami-m分布的条件下,推导出系统的中断概率闭合表达式。然后,为了进一步分析系统性能,还推导了高信噪比条件下系统的中断概率近似表达式。最后,计算机仿真验证了理论分析的正确性和所提方案的优越性。Abstract: Multi-user transmission system combined multi-antenna beamforming with cooperative Non-Orthogonal Multiple Access (NOMA) technique is investigated for Unmanned Aerial Vehicle (UAV) assisted satellite communication system. Firstly, in case that UAV employs multi-antenna and NOMA technique to serve multiple users, a beamforming scheme is proposed to maximize the average signal-to-interference-plus-noise ratio by using angle information of users. Secondly, under the condition that the satellite - UAV link follows the correlated Shadowed-Rician fading while the UAV - terrestrial link follows Nakagami-m fading, the closed-form expressions of outage probability for system are derived. Furthermore, the asymptotic outage probability formulas in the high signal-to-noise ratio regime are also developed to analyze the system performance. Finally, computer simulations are provided to validate the correctness of the theoretical analysis and the superiority of the proposed scheme.
-
表 1 系统的参数设置
参数 数值 卫星波束最大增益$G_{\rm{S}}^{{\rm{max}}}{\text{ } }\left( { {\text{dB} } } \right)$ 53 3 dB角度${\theta _{ { {\rm{S} } } ,3\;{\text{dB} } } }$(o) 0.4 带宽$B{\text{ }}\left( {{\text{MHz}}} \right)$ 5 无人机与地面用户间距离${d_{l,n}}{\text{ }}\left( {\text{m}} \right)$ 500 噪声温度$T{\text{ }}\left( {\text{K}} \right)$ 300 -
[1] LIN Min, LIN Zhi, ZHU Weiping, et al. Joint beamforming for secure communication in cognitive satellite terrestrial networks[J]. IEEE Journal on Selected Areas in Communications, 2018, 36(5): 1017–1029. doi: 10.1109/JSAC.2018.2832819 [2] LIN Zhi, LIN Min, DE COLA T, et al. Supporting IoT with rate-splitting multiple access in satellite and aerial-integrated networks[J]. IEEE Internet of Things Journal, 2021, 8(14): 11123–11134. doi: 10.1109/JIOT.2021.3051603 [3] 席博, 洪涛, 张更新. 卫星物联网场景下基于节点选择的协作波束成形技术研究[J]. 电子与信息学报, 2020, 42(12): 2882–2890. doi: 10.11999/JEIT190707XI Bo, HONG Tao, and ZHANG Gengxin. Research on the collaborative beamforming technique based on the node selection for satellite internet of things[J]. Journal of Electronics &Information Technology, 2020, 42(12): 2882–2890. doi: 10.11999/JEIT190707 [4] 徐常志, 靳一, 李立, 等. 面向6G的星地融合无线传输技术[J]. 电子与信息学报, 2021, 43(1): 28–36. doi: 10.11999/JEIT200363XU Changzhi, JIN Yi, LI Li, et al. Wireless transmission technology of satellite-terrestrial integration for 6G mobile communication[J]. Journal of Electronics &Information Technology, 2021, 43(1): 28–36. doi: 10.11999/JEIT200363 [5] BHATNAGAR M R and ARTI M K. Performance analysis of hybrid satellite-terrestrial FSO cooperative system[J]. IEEE Photonics Technology Letters, 2013, 25(22): 2197–2200. doi: 10.1109/LPT.2013.2282836 [6] 袁祖霞, 林敏, 刘笑宇, 等. 基于多用户反馈的星地协作传输系统性能分析[J]. 系统工程与电子技术, 2021, 43(4): 1089–1098. doi: 10.12305/j.issn.1001-506x.2021.04.27YUAN Zuxia, LIN Min, LIU Xiaoyu, et al. Performance analysis of a hybrid satellite-terrestrial cooperative networks with multiuser feedback[J]. Systems Engineering and Electronics, 2021, 43(4): 1089–1098. doi: 10.12305/j.issn.1001-506x.2021.04.27 [7] HUANG Qingquan, LIN Min, ZHU Weiping, et al. Uplink massive access in mixed RF/FSO satellite-aerial-terrestrial networks[J]. IEEE Transactions on Communications, 2021, 69(4): 2413–2426. doi: 10.1109/TCOMM.2021.3049364 [8] 贾向东, 路艺, 纪澎善, 等. 大规模无人机协助的多层异构网络设计及性能研究[J]. 电子与信息学报, 2021, 43(9): 2632–2639. doi: 10.11999/JEIT200443JIA Xiangdong, LU Yi, JI Pengshan, et al. Design of large-scale UAV-assisted multi-tier heterogeneous networks and performance research[J]. Journal of Electronics &Information Technology, 2021, 43(9): 2632–2639. doi: 10.11999/JEIT200443 [9] KONG Huaicong, LIN Min, ZHU Weiping, et al. Multiuser scheduling for asymmetric FSO/RF links in satellite-UAV-terrestrial networks[J]. IEEE Wireless Communications Letters, 2020, 9(8): 1235–1239. doi: 10.1109/LWC.2020.2986750 [10] LIU Xiaoyu, LIN Min, HUANG Qingquan, et al. Performance analysis for multi-user integrated satellite and UAV cooperative networks[J]. Physical Communication, 2019, 36: 100762. doi: 10.1016/j.phycom.2019.100762 [11] SHARMA P K, DEEPTHI D, and KIM D I. Outage probability of 3-D mobile UAV relaying for hybrid satellite-terrestrial networks[J]. IEEE Communications Letters, 2020, 24(2): 418–422. doi: 10.1109/LCOMM.2019.2956526 [12] LIN Zhi, LIN Min, WANG Junbo, et al. Joint beamforming and power allocation for satellite-terrestrial integrated networks with non-orthogonal multiple access[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(3): 657–670. doi: 10.1109/JSTSP.2019.2899731 [13] HAN Lve, ZHU Weiping, and LIN Min. Outage of NOMA-based hybrid satellite-terrestrial multi-antenna DF relay networks[J]. IEEE Wireless Communications Letters, 2021, 10(5): 1083–1087. doi: 10.1109/LWC.2021.3058005 [14] ZHANG Xiaokai, GUO Daoxing, AN Kang, et al. Performance analysis of NOMA-based cooperative spectrum sharing in hybrid satellite-terrestrial networks[J]. IEEE Access, 2019, 7: 172321–172329. doi: 10.1109/ACCESS.2019.2956185 [15] LI Xingwang, LI Jingjing, LIU Yuanwei, et al. Residual transceiver hardware impairments on cooperative NOMA networks[J]. IEEE Transactions on Wireless Communications, 2020, 19(1): 680–695. doi: 10.1109/TWC.2019.2947670 [16] BADRUDEEN A A, LEOW C Y, and WON S H. Performance analysis of hybrid beamforming precoders for multiuser millimeter wave NOMA systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(8): 8739–8752. doi: 10.1109/TVT.2020.3000443 [17] WANG Changqing, YANG Xiangyu, DU Quancheng, et al. Outage performance of satellite-UAV network framework based on NOMA[C]. The 2021 IEEE 5th International Conference on Cryptography, Security and Privacy, Zhuhai, China, 2021: 171–175. [18] ALAVI F, CUMANAN K, FOZOONI M, et al. Robust energy-efficient design for MISO non-orthogonal multiple access systems[J]. IEEE Transactions on Communications, 2019, 67(11): 7937–7949. doi: 10.1109/TCOMM.2019.2931972 [19] HUANG Qingquan, LIN Min, WANG Junbo, et al. Outage performance of satellite-aerial-terrestrial network[C]. 2019 IEEE Globecom Workshops, Waikoloa, USA, 2019: 1–6. [20] WANG Zhengdao and GIANNAKIS G B. A simple and general parameterization quantifying performance in fading channels[J]. IEEE Transactions on Communications, 2003, 51(8): 1389–1398. doi: 10.1109/TCOMM.2003.815053 [21] GRADSHTEYN I S and RYZHIK I M. Table of Integrals, Series, and Products[M]. 7th ed. Burlington: Academic, 2007. -





 下载:
下载:





 下载:
下载:
