多扩展目标跟踪中基于多特征优化的传感器控制方法

陈辉; 魏凤旗; 韩崇昭

doi:10.11999/JEIT211244

多扩展目标跟踪中基于多特征优化的传感器控制方法

doi: 10.11999/JEIT211244

1.
兰州理工大学电气工程与信息工程学院兰州 730050
2.
西安交通大学自动化科学与工程学院西安 710049

基金项目: 国家自然科学基金 (62163023, 61763029, 61873116)，甘肃省教育厅产业支撑计划项目(2021CYZC-02)

详细信息

作者简介:
陈辉：男，教授，博士生导师，主要研究方向为认知对抗、数据融合、最优控制等

魏凤旗：男，硕士生，研究方向为数据融合与多目标跟踪技术

韩崇昭：男，教授，博士生导师，主要研究方向为数据融合、电子对抗、雷达目标跟踪等

通讯作者:
陈辉　huich78@hotmail.com

中图分类号: TN911.73; TP274
计量
- 文章访问数: 539
- HTML全文浏览量: 143
- PDF下载量: 66
- 被引次数: 0
出版历程
- 收稿日期: 2021-11-09
- 修回日期: 2022-06-02
- 录用日期: 2022-06-22
- 网络出版日期: 2022-06-29
- 刊出日期: 2023-01-17

Sensor Control Based on Multiple Feature Optimization in Multiple Extended Targets Tracking

1.
School of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China
2.
School of Automation Science and Engineering, Xi'an Jiaotong University, Xi’an 710049, China

Funds: The National Natural Science Foundation of China (62163023, 61763029, 61873116), The Industrial Support Project of Education Department of Gansu Province (2021CYZC-02)

摘要

摘要: 针对多扩展目标的优化跟踪问题，该文在有限集统计(FISST)理论框架下，提出一种能够综合优化多扩展目标跟踪性能的传感器控制方法。首先，该文给出加权广义最优子模式分配(WGOSPA)距离构造多扩展目标跟踪多特征估计在其统计平均周围的广义离差，进而研究提出多特征融合下的传感器控制最优决策方法，并利用序贯蒙特卡罗(SMC)技术研究传感器控制最优决策过程的数值求解方法，然后利用伽马高斯逆威沙特多伯努利(GGIW-MBer)滤波器实现所提出的传感器控制策略。最后通过仿真实验验证了所提算法的有效性。
- 传感器控制 /
- 多扩展目标跟踪 /
- 评价函数 /
- 有限集统计 /
- 伽马高斯逆威沙特混合
Abstract: Focusing on the optimal tracking problem of multiple extended targets, a sensor control method is proposed, which can comprehensively optimize the tracking performance of multiple extended targets in the framework of FInite Set STatistics (FISST). First, a Weighted Generalized Optimal Sub-Pattern Assignment (WGOSPA) distance is proposed to construct multiple extended targets tracking multiple feature estimation of generalized dispersion around its statistical average. In addition, an optimal decision-making method of sensor control through the multi-characteristic fusion is studied and proposed. Furthermore, the numerical solution method of the optimal decision-making process of sensor control is studied by using Sequential Monte Carlo (SMC) technology. Then, the proposed sensor control strategy is realized by using Gamma Gaussian Inverse Wishart Multi-Bernoulli (GGIW-MBer) filter. Finally, the effectiveness of the proposed algorithm is verified by simulation experiments.
- Sensor control /
- Multiple extended targets tracking /
- Evaluation function /
- Finite set statistics /
- Gamma Gaussian Inverse Wishart mixture

HTML全文

图 1 多扩展目标跟踪中的传感器控制基本原理图

下载: 全尺寸图片幻灯片

图 2 传感器动作空间示意图

下载: 全尺寸图片幻灯片

图 3 目标的实际轨迹

下载: 全尺寸图片幻灯片

图 4 方案2中的传感器运动轨迹

下载: 全尺寸图片幻灯片

图 5 MC实验中方案2传感器轨迹控制图

下载: 全尺寸图片幻灯片

图 6 目标质心位置估计GOSPA距离统计

下载: 全尺寸图片幻灯片

图 7 目标跟踪轨迹图

下载: 全尺寸图片幻灯片

图 8 椭圆长短轴GOSPA距离统计

下载: 全尺寸图片幻灯片

图 9 多扩展目标跟踪的势估计

下载: 全尺寸图片幻灯片

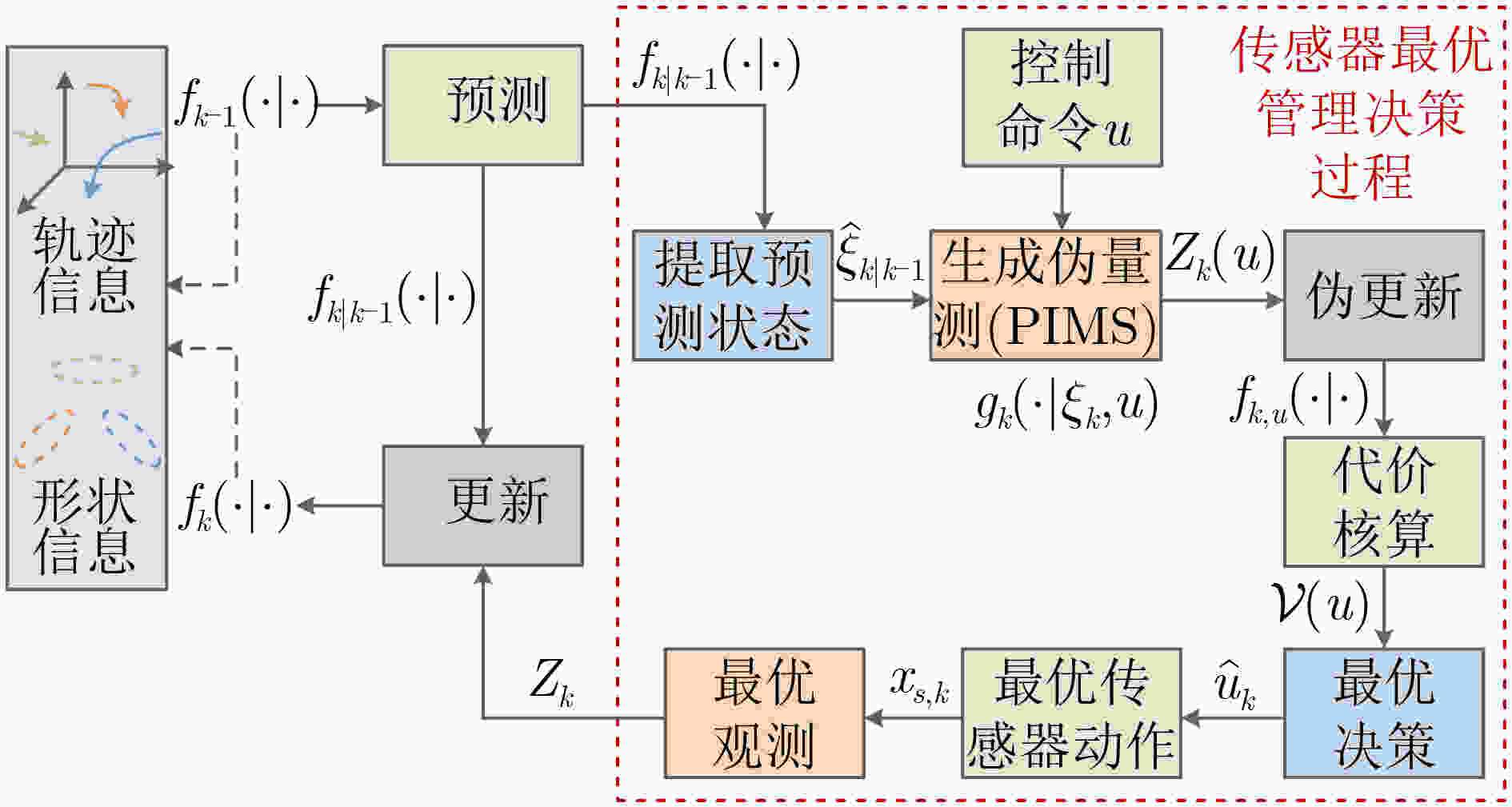
算法1　多扩展目标跟踪基于多特征优化的传感器控制算法
输入：$ k - 1 $时刻多扩展目标多特征信息$ {\zeta _{k - 1}} $与传感器坐标　　　　${x_{{\rm{s}},k - 1} }$，
其中，${\zeta _{k - 1} } = \left\{ { {\alpha _{k - 1} },{\beta _{k - 1} },{{\boldsymbol{m}}_{k - 1} },{{\boldsymbol{P}}_{k - 1} },{{\boldsymbol{v}}_{k - 1} },{{\boldsymbol{V}}_{k - 1} } } \right\}$。
(1) 多扩展目标跟踪的预测过程，得到$ {f_{k\|k - 1}}\left( { \cdot \| \cdot } \right) $。
(2) 传感器控制
$ {\hat \xi _{k\|k - 1}} = {\text{Sef}}\left\{ {{f_{k\|k - 1}}\left( { \cdot \| \cdot } \right)} \right\} $，
确定所有可能的控制方案${{\boldsymbol{U}}_k}$。
${\text{for all } }u \in {{\boldsymbol{U}}_k}{\text{ do} }$
生成PIMS：${{\boldsymbol{Z}}_k}\left( u \right)$，
量测集划分：${\boldsymbol{\rho}} \angle {{\boldsymbol{Z}}_k}\left( u \right)$，
计算伪更新后验密度$ {f_{k,u}}\left( { \cdot \| \cdot } \right) $，
提取状态的统计平均：$ {\bar \xi _{k,u}} \leftarrow {\text{Sef}}\left\{ {{f_{k,u}}\left( { \cdot \| \cdot } \right)} \right\} $，
蒙特卡罗采样：$ \left\{ {{\xi _{k,l}}} \right\}_{l = 1}^L \leftarrow {\text{MC}}\left( {{f_{k,u}}\left( { \cdot \| \cdot } \right),L} \right) $，
$ \mathcal{V}\left( u \right) \leftarrow 0 $，
$ {\text{for }}l = 1:L $
$\mathcal{V}\left( u \right) \leftarrow \mathcal{V}\left( u \right) + \dfrac{1}{L}d_p^{\left( { {c_w},\alpha } \right)}\left( { {\xi _{k,l} },{ {\bar \xi }_{k,u} } } \right)$。
$ {\text{end for}} $
$ {\text{end for}} $ 　$ {\hat u_k} \leftarrow \mathop {\arg \min }\limits_{u \in {U_k}} \mathcal{V}\left( u \right) $。
(3) 多扩展目标跟踪的更新过程，得到$ {f_{k\|k}}\left( { \cdot \| \cdot } \right) $。
(4) 提取状态信息$ {\xi _k} $，并计算目标势$ {N_k} = \left\| {{\xi _k}} \right\| $。
输出：目标势$ {N_k} $，多扩展目标状态集$ {\xi _k} $，$ k $时刻传感器坐标　　　　${x_{{\rm{s}},k} }$。

下载: 导出CSV

算法2　GGIW-MBer预测过程
输入：$ \zeta _{k - 1}^{\left( {i,j} \right)} $。
预测第$ j $个GGIW分量的参数：
${\boldsymbol{m}}_{k\|k - 1}^{\left( {i,j} \right)} = {{\boldsymbol{F}}_{k\|k - 1} }{\boldsymbol{m}}_{k - 1}^{\left( {i,j} \right)}$
${\boldsymbol{P}}_{k\|k - 1}^{\left( {i,j} \right)} = {{\boldsymbol{F}}_{k\|k - 1} }{\boldsymbol{P}}_{k - 1}^{\left( {i,j} \right)}{\boldsymbol{F}}_{k\|k - 1}^{\text{T} } + {{\boldsymbol{Q}}_k}$
$v_{k\|k - 1}^{\left( {i,j} \right)} = {{\rm{e}}^{ - \frac{ { {T_{\rm{s}}} } }{\tau } } }v_{k - 1}^{\left( {i,j} \right)}$
$V_{k\|k - 1}^{\left( {i,j} \right)} = \dfrac{ {v_{k\|k - 1}^{\left( {i,j} \right)} - d - 1} }{ {v_{k - 1}^{\left( {i,j} \right)} - d - 1} }V_{k - 1}^{\left( {i,j} \right)}$
$X_{k\|k - 1}^{\left( {i,j} \right)} = \dfrac{ {V_{k\|k - 1}^{\left( {i,j} \right)} } }{ {v_{k\|k - 1}^{\left( {i,j} \right)} - 2d - 2} }$
$\alpha _{k\|k - 1}^{\left( {i,j} \right)} = \dfrac{ {\alpha _{k - 1}^{\left( {i,j} \right)} } }{ { {\eta _{k - 1} } } }$
$\beta _{k\|k - 1}^{\left( {i,j} \right)} = \dfrac{ {\beta _{k - 1}^{\left( {i,j} \right)} } }{ { {\eta _{k - 1} } } }$
输出：$ \zeta _{k\|k - 1}^{\left( {i,j} \right)} $。

下载: 导出CSV

算法3　GGIW-MBer更新过程
输入：$ \zeta _{k\|k - 1}^{\left( {i,j} \right)} $，量测集划分${\boldsymbol{W}}$。
更新第$ j $个GGIW分量的参数：　$\bar z_k^W = \dfrac{1}{ {\left\| {\boldsymbol{W} } \right\|} }\displaystyle\sum\limits_{z_k^{\left( i \right)} \in W} { {\boldsymbol{z} }_k^{\left( i \right)} }$
${\boldsymbol{X}}_{k\|k - 1}^{\left( {i,j} \right)} = \dfrac{ {{\boldsymbol{V}}_{k\|k - 1}^{\left( {i,j} \right)} } }{ {v_{k\|k - 1}^{\left( {i,j} \right)} - 2d - 2} }$
${\boldsymbol{S} }_{k\|k - 1}^{\left( {i,j,W} \right)} = { {\boldsymbol{H} }_k}{\boldsymbol{P} }_{k\|k - 1}^{\left( {i,j} \right)}{\boldsymbol{H} }_k^{\text{T} } + \dfrac{ { {\boldsymbol{X} }_{k\|k - 1}^{\left( {i,j} \right)} } }{ {\left\| {\boldsymbol{W} } \right\|} }$
${\boldsymbol{K}}_{k\|k - 1}^{\left( {i,j,W} \right)} = {\boldsymbol{P}}_{k\|k - 1}^{\left( {i,j} \right)}{\boldsymbol{H}}_k^{\text{T} }{\left( {{\boldsymbol{S}}_{k\|k - 1}^{\left( {i,j,W} \right)} } \right)^{ - 1} }$
${\boldsymbol{\varepsilon}} _{k\|k - 1}^{\left( {i,j,W} \right)} = \bar {\boldsymbol{z}}_k^W - {{\boldsymbol{H}}_k}{\boldsymbol{m}}_{k\|k - 1}^{\left( {i,j} \right)}$
${\boldsymbol{m}}_k^{\left( {i,j} \right)} = {\boldsymbol{m}}_{k\|k - 1}^{\left( {i,j} \right)} + {\boldsymbol{K}}_{k\|k - 1}^{\left( {i,j,W} \right)}{\boldsymbol{\varepsilon}} _{k\|k - 1}^{\left( {i,j,W} \right)}$
${\boldsymbol{P}}_k^{\left( {i,j} \right)} = {\boldsymbol{P}}_{k\|k - 1}^{\left( {i,j} \right)} - {\boldsymbol{K}}_{k\|k - 1}^{\left( {i,j,W} \right)}{\boldsymbol{S}}_{k\|k - 1}^{\left( {i,j,W} \right)}{\left( {{\boldsymbol{K}}_{k\|k - 1}^{\left( {i,j,W} \right)} } \right)^{\text{T} } }$
${\boldsymbol{Z}}_k^W = \displaystyle\sum\limits_{z_k^{\left( i \right)} \in W} {\left( {{\boldsymbol{z}}_k^{\left( i \right)} - \bar {\boldsymbol{z}}_k^W} \right){ {\left( {{\boldsymbol{z}}_k^{\left( i \right)} - \bar {\boldsymbol{z}}_k^W} \right)}^{\text{T} } } }$
$\begin{aligned} {\boldsymbol{N} }_{k\|k - 1}^{\left( {i,j,W} \right)} =& {\left( { {\boldsymbol{X} }_{k\|k - 1}^{\left( {i,j} \right)} } \right)^{\frac{1}{2} } }{\left( { {\boldsymbol{S} }_{k\|k - 1}^{\left( {i,j,W} \right)} } \right)^{ - \frac{1}{2} } }{\boldsymbol{\varepsilon} } _{k\|k - 1}^{\left( {i,j,W} \right)}{\text{ } } \times {\left( { {\boldsymbol{\varepsilon} } _{k\|k - 1}^{\left( {i,j,W} \right)} } \right)^{\text{T} } }\\ & \cdot{\left(\left( { {\boldsymbol{S} }_{k\|k - 1}^{\left( {i,j,W} \right)} } \right)^{ -\frac {1} {2} } \right)^{ {\rm{T} } } }\left({\left( { {\boldsymbol{X} }_{k\|k - 1}^{\left( {i,j} \right)} } \right)^{\frac{ 1}{2} } }\right)^{\rm{T} }\end{aligned}$
$v_k^{\left( {i,j,W} \right)} = v_{k\|k - 1}^{\left( {i,j,W} \right)} + \left\| {\boldsymbol{W}} \right\|$
${\boldsymbol{V}}_k^{\left( {i,j,W} \right)} = {\boldsymbol{V}}_{k\|k - 1}^{\left( {i,j,W} \right)} + {\boldsymbol{N}}_{k\|k - 1}^{\left( {i,j,W} \right)} + {\boldsymbol{Z}}_k^W$ 　${\boldsymbol{X} }_k^{\left( {i,j,W} \right)} = \dfrac{ { {\boldsymbol{V} }_k^{\left( {i,j,W} \right)} } }{ {v_k^{\left( {i,j,W} \right)} - 2d - 2} }$
$\alpha _k^{\left( {i,j,W} \right)} = \alpha _{k\|k - 1}^{\left( {i,j,W} \right)} + \left\| {\boldsymbol{W}} \right\|$
$ \beta _k^{\left( {i,j,W} \right)} = \beta _{k\|k - 1}^{\left( {i,j,W} \right)} + 1 $
输出：$ \zeta _k^{\left( {i,j} \right)} $。

下载: 导出CSV

表 1 多扩展目标初始参数

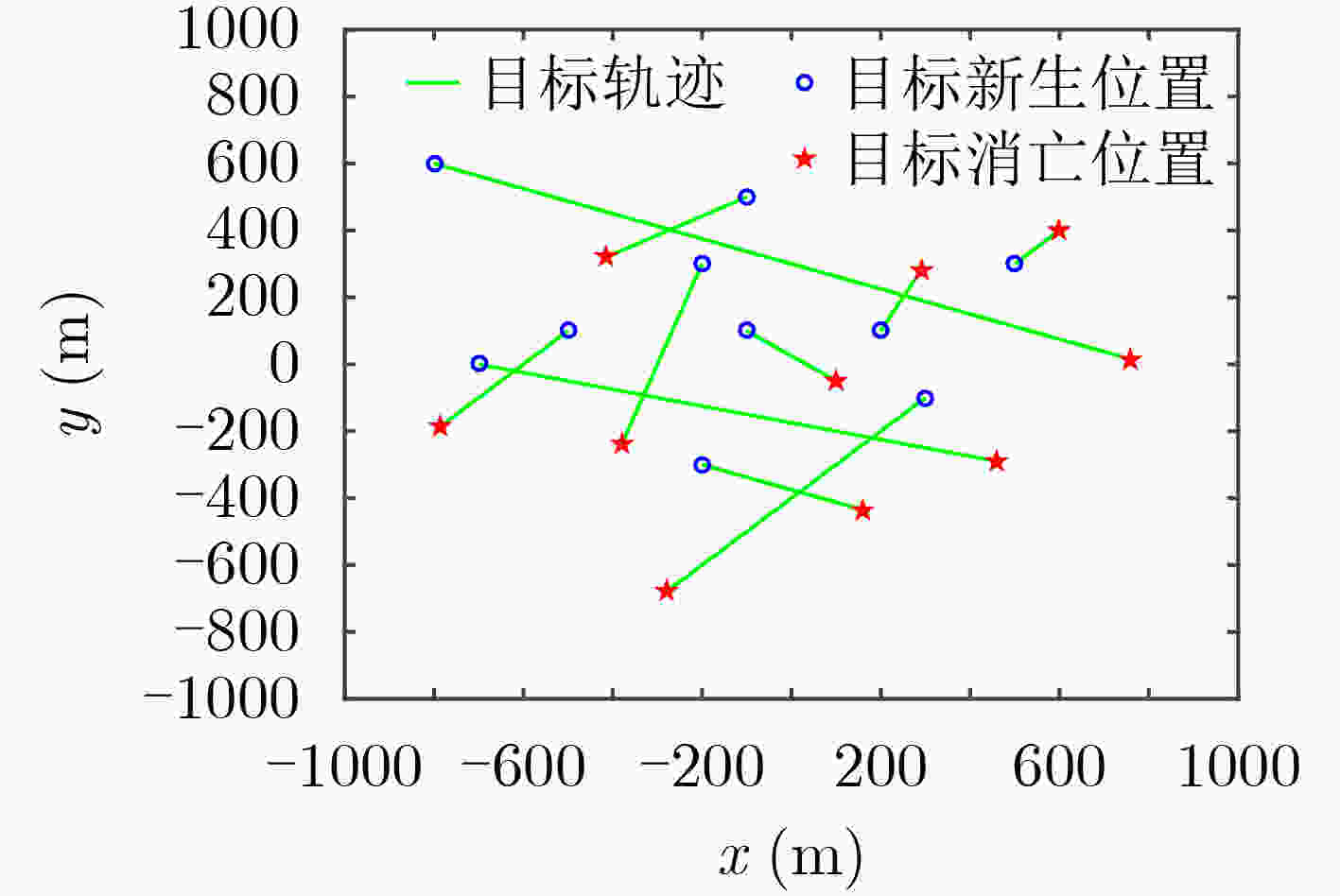
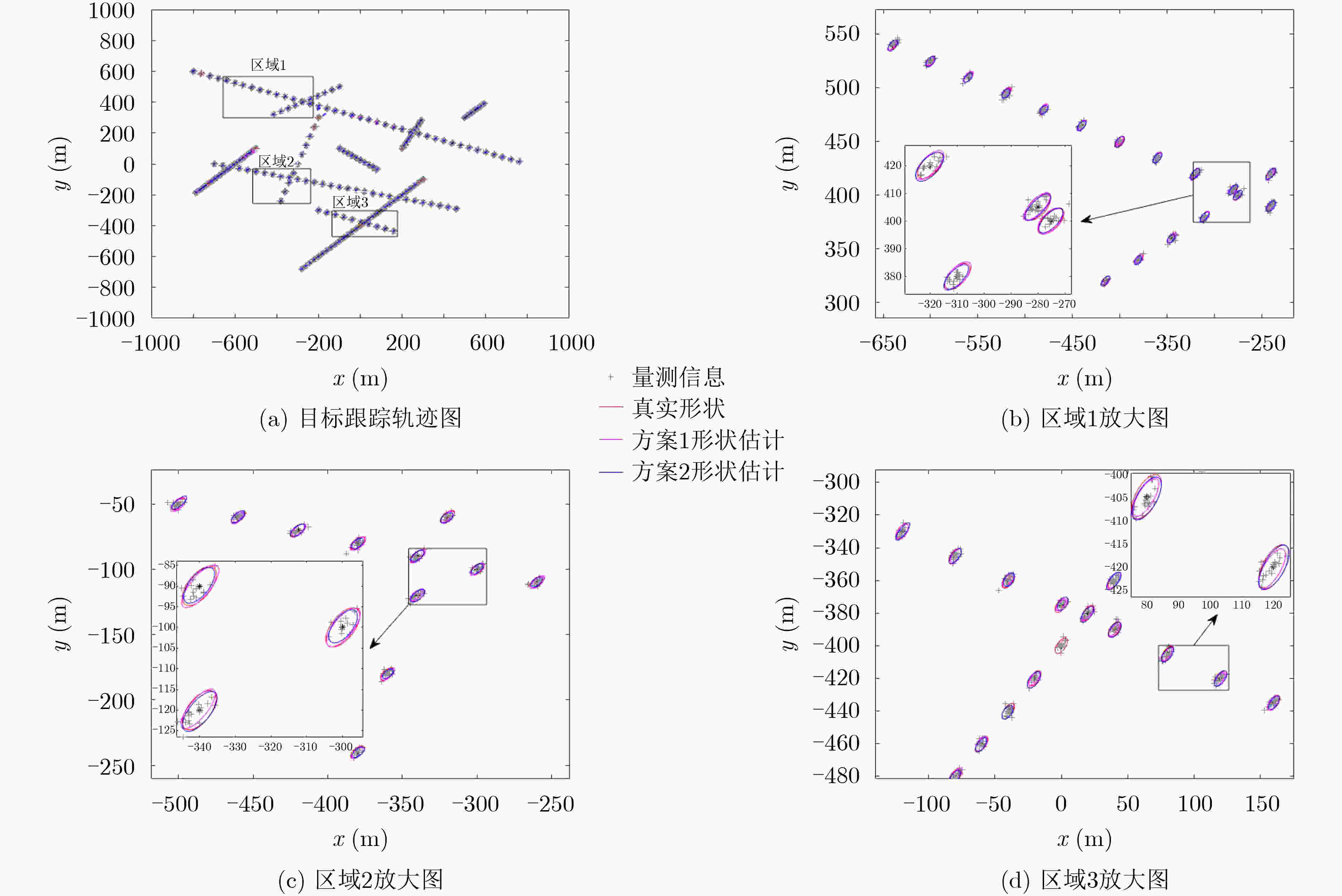
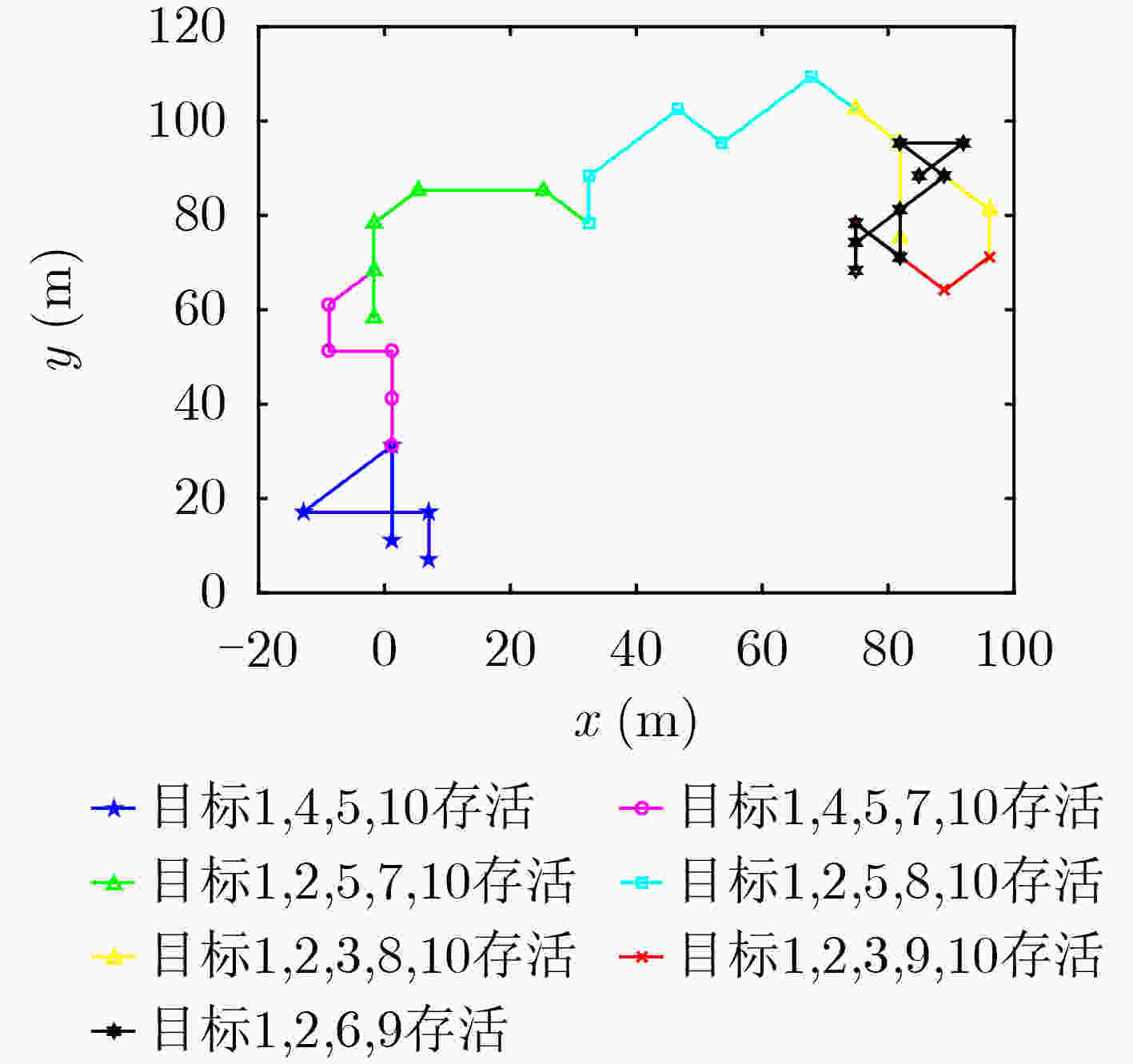
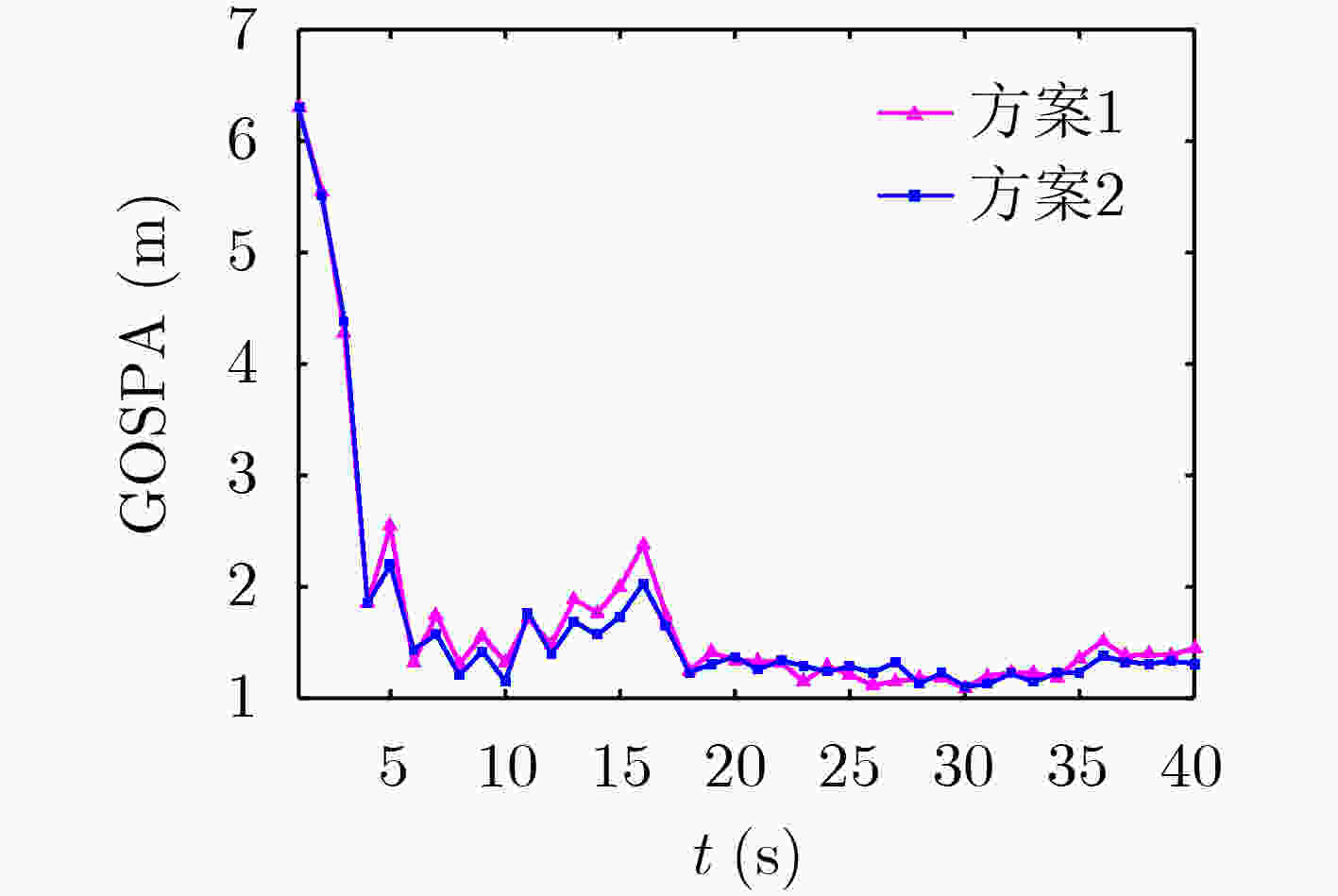
目标	出生时刻 (s)	消亡时刻 (s)	初始状态 (m; m; m/s; m/s)
1	1	40	[–800; 600; 40; –15]
2	11	40	[–700; 0; 40; –10]
3	21	30	[–100; 500; –35; –20]
4	1	10	[200; 100; 10; 20]
5	1	20	[–500; 100; –15; –15]
6	31	40	[–100; 100; 20; –15]
7	6	15	[500; 300; 10; 10]
8	16	25	[–200; 300; –20; –60]
9	26	35	[–200; –300; 40; –15]
10	1	30	[300; –100; –20; –20]

下载: 导出CSV

表 2 目标质心估计的GOSPA距离统计均值(m)

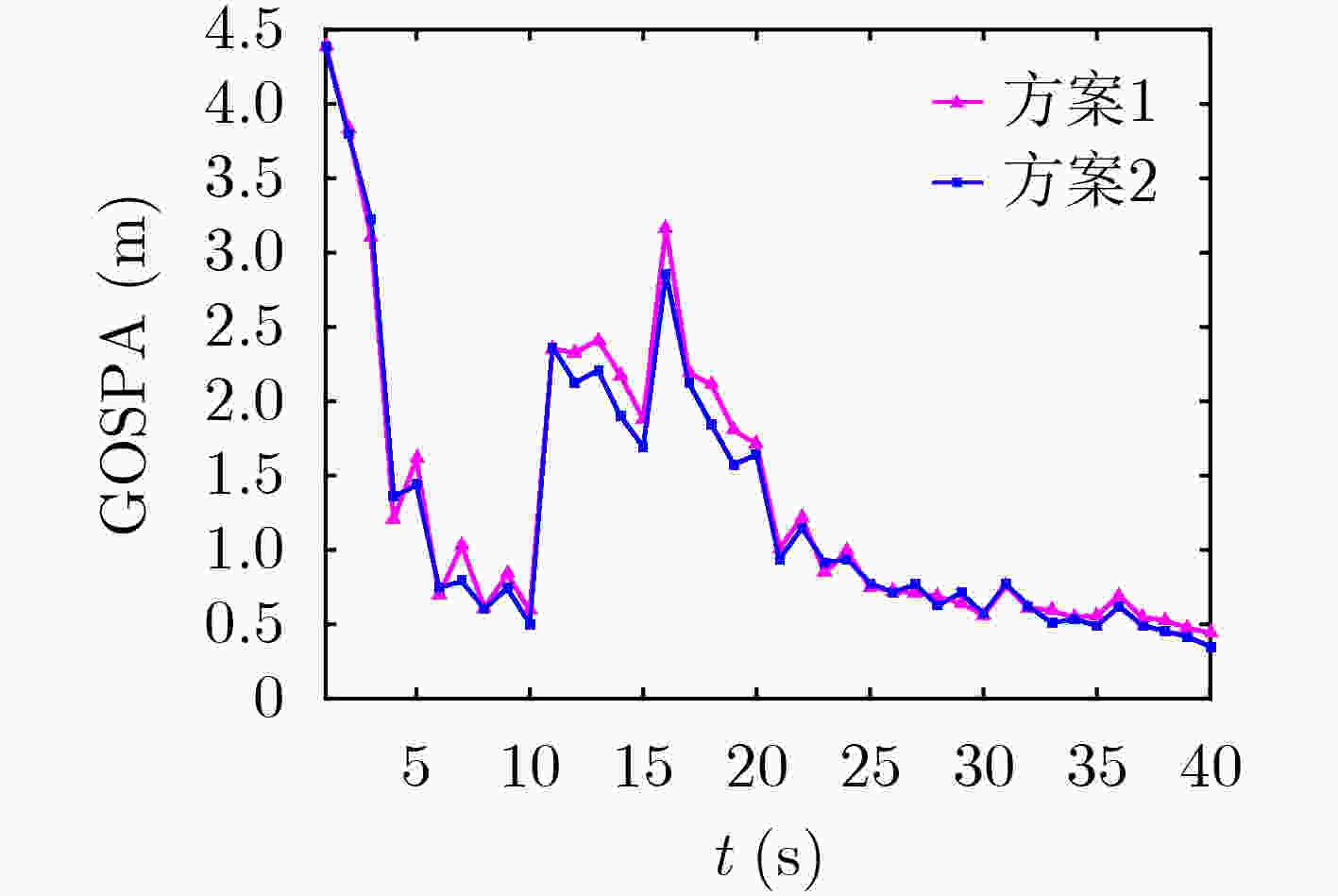
	方案1	方案2
GOSPA距离	1.1303	1.0671

下载: 导出CSV

表 3 目标长短轴的GOSPA距离统计平均值(m)

	方案1	方案2
GOSPA距离	1.5594	1.5009

下载: 导出CSV

参考文献(30)

[1]	SHIN D, SONG Y, OH J, et al. Nonlinear disturbance observer-based standoff target tracking for small fixed-wing UAVs[J]. International Journal of Aeronautical and Space Sciences, 2021, 22(1): 108–119. doi: 10.1007/s42405-020-00275-6
[2]	KIM D Y, VO B N, VO B T, et al. A labeled random finite set online multi-object tracker for video data[J]. Pattern Recognition, 2019, 90: 377–389. doi: 10.1016/j.patcog.2019.02.004
[3]	陈辉, 邓东明, 韩崇昭. 基于区间箱粒子多伯努利滤波器的传感器控制策略[J]. 自动化学报, 2021, 47(6): 1428–1443. doi: 10.16383/j.aas.c180541 CHEN Hui, DENG Dongming, and HAN Chongzhao. Sensor control based on interval box-particle multi-Bernoulli filter[J]. Acta Automatica Sinica, 2021, 47(6): 1428–1443. doi: 10.16383/j.aas.c180541
[4]	陈辉, 李国财, 韩崇昭, 等. 高斯过程回归模型多扩展目标多伯努利滤波器[J]. 控制理论与应用, 2020, 37(9): 1931–1943. doi: 10.7641/CTA.2020.90978 CHEN Hui, LI Guocai, HAN Chongzhao, et al. A multiple extended target multi-Bernouli filter based on Gaussian process regression model[J]. Control Theory &Applications, 2020, 37(9): 1931–1943. doi: 10.7641/CTA.2020.90978
[5]	CORALUPPI S, CARTHEL C, KREAMER W, et al. New graph-based and MCMC approaches to multi-INT surveillance[C]. The 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 2016: 394–401.
[6]	BOSTRÖM-ROST P, AXEHILL D, and HENDEBY G. PMBM filter with partially grid-based birth model with applications in sensor management[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(1): 530–540. doi: 10.1109/TAES.2021.3103255
[7]	HERO A O and COCHRAN D. Sensor management: Past, present, and future[J]. IEEE Sensors Journal, 2011, 11(12): 3064–3075. doi: 10.1109/JSEN.2011.2167964
[8]	陈辉, 韩崇昭. 机动多目标跟踪中的传感器控制策略的研究[J]. 自动化学报, 2016, 42(4): 512–523. doi: 10.16383/j.aas.2016.c150529 CHEN Hui and HAN Chongzhao. Sensor control strategy for maneuvering multi-target tracking[J]. Acta Automatica Sinica, 2016, 42(4): 512–523. doi: 10.16383/j.aas.2016.c150529
[9]	罗开平, 姜维, 李一军. 传感器管理述评[J]. 电子学报, 2010, 38(8): 1900–1907. LUO Kaiping, JIANG Wei, and LI Yijun. Review of sensor management[J]. Acta Electronica Sinica, 2010, 38(8): 1900–1907.
[10]	MAHLER R P S. Advances in Statistical Multisource-Multitarget Information Fusion[M]. Boston: Artech House, 2014: 825–860.
[11]	MAHLER R P S. Statistical Multisource-Multitarget Information Fusion[M]. Boston: Artech House, 2007: 655–667.
[12]	杨威, 付耀文, 龙建乾, 等. 基于有限集统计学理论的目标跟踪技术研究综述[J]. 电子学报, 2012, 40(7): 1440–1448. doi: 10.3969/j.issn.0372-2112.2012.07.025 YANG Wei, FU Yaowen, LONG Jianqian, et al. The FISST-based target tracking techniques: A survey[J]. Acta Electronica Sinica, 2012, 40(7): 1440–1448. doi: 10.3969/j.issn.0372-2112.2012.07.025
[13]	AUGHENBAUGH J M and LA COUR B R. Metric selection for information theoretic sensor management[C]. The 11th International Conference on Information Fusion, Cologne, Germany, 2008: 1–8.
[14]	HOANG H G, VO B N, VO B T, et al. The Cauchy–Schwarz divergence for Poisson point processes[J]. IEEE Transactions on Information Theory, 2015, 61(8): 4475–4485. doi: 10.1109/TIT.2015.2441709
[15]	陈辉, 贺忠良, 邓东明, 等. 高斯混合多伯努利滤波器基于柯西施瓦兹散度的传感器控制方法[J]. 电子学报, 2020, 48(4): 706–716. doi: 10.3969/j.issn.0372-2112.2020.04.012 CHEN Hui, HE Zhongliang, DENG Dongming, et al. Sensor control using Cauchy-Schwarz divergence via Gaussian mixture multi-Bernoulli filter[J]. Acta Electronica Sinica, 2020, 48(4): 706–716. doi: 10.3969/j.issn.0372-2112.2020.04.012
[16]	RISTIC B, VO B N, and CLARK D. A note on the reward function for PHD filters with sensor control[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1521–1529. doi: 10.1109/TAES.2011.5751278
[17]	陈辉, 贺忠良, 连峰, 等. 多目标跟踪中基于目标威胁度评估的传感器控制方法[J]. 电子与信息学报, 2018, 40(12): 2861–2867. doi: 10.11999/JEIT180212 CHEN Hui, HE Zhongliang, LIAN Feng, et al. Threat assessment based sensor control for multi-target tracking[J]. Journal of Electronics &Information Technology, 2018, 40(12): 2861–2867. doi: 10.11999/JEIT180212
[18]	KATSILIERIS F, DRIESSEN H, and YAROVOY A. Threat-based sensor management for target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 2772–2785. doi: 10.1109/TAES.2015.140052
[19]	HOANG H G and VO B T. Sensor management for multi-target tracking via multi-Bernoulli filtering[J]. Automatica, 2014, 50(4): 1135–1142. doi: 10.1016/j.automatica.2014.02.007
[20]	GOSTAR A K, HOSEINNEZHAD R, and BAB-HADIASHAR A. Multi-Bernoulli sensor control via minimization of expected estimation errors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 1762–1773. doi: 10.1109/TAES.2015.140211
[21]	MAHLER R P S and ZAJIC T R. Probabilistic objective functions for sensor management[J]. SPIE, 2004, 233–244.
[22]	KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042–1059. doi: 10.1109/TAES.2008.4655362
[23]	FELDMANN M, FRÄNKEN D, and KOCH W. Tracking of extended objects and group targets using random matrices[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1409–1420. doi: 10.1109/TSP.2010.2101064
[24]	TUNCER B and ÖZKAN E. Random matrix based extended target tracking with orientation: A new model and inference[J]. IEEE Transactions on Signal Processing, 2021, 69: 1910–1923. doi: 10.1109/TSP.2021.3065136
[25]	BAUM M and HANEBECK U D. Random hypersurface models for extended object tracking[C]. 2009 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajaman, United Arab Emirates, 2009: 178–183.
[26]	WAHLSTRÖM N and ÖZKAN E. Extended target tracking using Gaussian processes[J]. IEEE Transactions on Signal Processing, 2015, 63(16): 4165–4178. doi: 10.1109/TSP.2015.2424194
[27]	陈辉, 杜金瑞, 韩崇昭. 基于星凸形随机超曲面模型多扩展目标多伯努利滤波器[J]. 自动化学报, 2020, 46(5): 909–922. doi: 10.16383/j.aas.c180130 CHEN Hui, DU Jinrui, and HAN Chongzhao. A multiple extended target multi-bernouli filter based on star-convex random hypersurface model[J]. Acta Automatica Sinica, 2020, 46(5): 909–922. doi: 10.16383/j.aas.c180130
[28]	MAHLER R. PHD filters for nonstandard targets, I: Extended targets[C]. The 12th International Conference on Information Fusion, Seattle, USA, 2009: 915–921.
[29]	GOSTAR A K, HOSEINNEZHAD R, BAB-HADIASHAR A, et al. Sensor-management for multitarget filters via minimization of posterior dispersion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(6): 2877–2884. doi: 10.1109/TAES.2017.2718280
[30]	RAHMATHULLAH A S, GARCÍA-FERNÁNDEZ Á F, and SVENSSON L. Generalized optimal sub-pattern assignment metric[C]. The 20th International Conference on Information Fusion (Fusion), Xi’an, China, 2017: 1–8.