A Method of Nonlinearity Estimation and Correction Based on Difference Filtering
-
摘要: 在线性调频连续波雷达系统中,各个器件的非理想特性使得信号的相位产生各种畸变,严重影响雷达的测距精度以及成像质量,需要经过一定的校正手段才能获得高精度的测量结果。该文针对线性调频连续波信号以及确定性非线性相位的特点,建立了受到非线性干扰的线性调频连续波信号模型,提出一种新的基于差分滤波的非线性估计方法能够对周期性及非周期性非线性进行同时估计,并利用匹配傅里叶变换(MFT)方法对非线性相位进行校正。通过仿真和对比分析,表明该方法与其他方法相比具有更高的估计精度,且在非线性度较大时也能够具有良好的校正效果。最后采用雷达的实测数据验证了该算法的有效性。Abstract: In the linear Frequency Modulation Continuous Waveform (FMCW) Radar system, due to the non-ideal characteristics of each instrument, the phase of the signal produces various distortions, which affects seriously the radar's ranging accuracy and imaging quality. It requires certain correction methods to obtain high-precision measurement results. In view of the characteristics of FMCW signal and deterministic nonlinear phase, this paper establishes a FMCW signal model subject to nonlinear interference, and proposes a new nonlinear estimation method based on difference filtering, which can simultaneously estimate periodic and non-periodic nonlinearities, and uses Matching Fourier Transform (MFT) method to correct the nonlinear phase. Simulation and comparative analysis show that this method has higher estimation accuracy than other methods, and it can also have a good correction effect when the nonlinearity is large. Finally, the actual measurement data of the radar is used to verify the effectiveness of the algorithm.
-
表 1 雷达系统仿真参数
参数名称 参数符号 数值 单位 频率范围 $ f $ 1~2.5 GHz 采样率 ${f}_{{\rm{s}}}$ 2.5 MHz 时宽 $ T $ 4 ms 带宽 $B$ 1.5 GHz 调频斜率 $K$ 375 GHz/s 目标时延 $\tau $ 2 us 表 2 雷达系统设计参数
参数名称 参数符号 数值 单位 频率范围 $f$ 450~2150 MHz 采样率 ${f_{\rm{s}}}$ 200 kHz 时宽 $T$ 4 ms 带宽 $B$ 1.7 GHz 调频斜率 $K$ 425 GHz/s -
[1] RIZIK A, TAVANTI E, VIO R, et al. Single target recognition using a low-cost FMCW radar based on spectrum analysis[C]. The 27th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 2020: 1–4. [2] LI Yabin, PENG Hongli, LI Mingming, et al. A miniaturized and high frequency response 35GHz FMCW radar for short range target detections[C]. 2020 IEEE Electrical Design of Advanced Packaging and Systems (EDAPS), Shenzhen, China, 2020: 1–3. [3] BI Hui, WANG Jingjing, and BI Guoan. Wavenumber domain algorithm-based FMCW SAR sparse imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(10): 7466–7475. doi: 10.1109/TGRS.2019.2913761 [4] WANG Shuai, WANG Bingnan, XIANG Maosheng, et al. Signal modeling and imaging of frequency-modulated continuous wave sliding spotlight synthetic aperture Ladar[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4007305. doi: 10.1109/LGRS.2020.3043747 [5] ZHAO Bo, ZHANG Yueyi, LANG Shinan, et al. Shallow-layers-detection ice sounding radar for mapping of polar ice sheets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 4301010. doi: 10.1109/TGRS.2021.3074186 [6] AYHAN S, SCHERR S, BHUTANI A, et al. Impact of frequency ramp nonlinearity, phase noise, and SNR on FMCW radar accuracy[J]. IEEE Transactions on Microwave Theory and Techniques, 2016, 64(10): 3290–3301. doi: 10.1109/TMTT.2016.2599165 [7] CHU Wei, LIU Yunqing, LI Xiaolong, et al. Phase estimation and correction of nonlinear sweep frequency for detecting vehicle targets with FMCW Radar[C]. The IEEE 6th International Conference on Computer and Communications (ICCC), Chengdu, China, 2020: 1273–1277. [8] LANG Shinan, CUI Xiangbin, ZHAO Yukai, et al. A novel range processing method of surface-based FMCW ice-sounding radar for accurately mapping the internal reflecting horizons in Antarctica[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 3633–3643. doi: 10.1109/JSTARS.2020.3004357 [9] ANGHEL A, VASILE G, CACOVEANU R, et al. Short-range wideband FMCW Radar for Millimetric displacement measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(9): 5633–5642. doi: 10.1109/TGRS.2013.2291573 [10] JIN Ke, LAI Tao, WANG Ting, et al. A method for nonlinearity correction of wideband FMCW radar[C]. Proceedings of 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 2016: 1–5. [11] WANG Rongrong, XIANG Maosheng, WANG Bingnan, et al. Nonlinear phase estimation and compensation for FMCW Ladar based on Synchrosqueezing wavelet transform[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(7): 1174–1178. doi: 10.1109/LGRS.2020.2997999 [12] META A, HOOGEBOOM P, and LIGTHART L. Range Non-linearities correction in FMCW SAR[C]. 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, USA, 2006: 403–406. [13] YANG Jian, LIU Chang, and WANG Yanfei. Nonlinearity correction of FMCW SAR based on homomorphic deconvolution[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 991–995. doi: 10.1109/LGRS.2012.2227667 [14] 赵志勇, 常文革, 黎向阳, 等. 去调频处理中空变相位误差补偿方法[J]. 国防科技大学学报, 2014, 36(3): 169–176. doi: 10.11887/j.cn.201403030ZHAO Zhiyong, CHANG Wenge, LI Xiangyang, et al. Range-dependent phase error compensation of dechirp[J]. Journal of National University of Defense Technology, 2014, 36(3): 169–176. doi: 10.11887/j.cn.201403030 [15] 郭文举. 宽带调频连续波雷达幅相误差估计与补偿技术[D]. [硕士论文], 北京理工大学, 2016.GUO Wenju. The amplitude and phase error estimation and compensation technology of wideband FMCW radar[D]. [Master dissertation], Beijing Institute of Technology, 2016. [16] 宿绍莹, 侯庆凯, 任艳, 等. 匹配滤波和去斜率脉压方法性能分析与比较[J]. 信号处理, 2011, 27(2): 202–206. doi: 10.3969/j.issn.1003-0530.2011.02.007SU Shaoying, HOU Qingkai, REN Yan, et al. Performance comparison of matched filtering and dechirp pulse compression[J]. Signal Processing, 2011, 27(2): 202–206. doi: 10.3969/j.issn.1003-0530.2011.02.007 [17] 耿淑敏, 江志红, 程翥, 等. FM-CW SAR距离-多普勒成像算法研究[J]. 电子与信息学报, 2007, 29(10): 2346–2349. doi: 10.3724/SP.J.1146.2006.00415GENG Shumin, JIANG Zhihong, CHENG Zhu, et al. Study on imaging algorithm of FM-CW SAR[J]. Journal of Electronics &Information Technology, 2007, 29(10): 2346–2349. doi: 10.3724/SP.J.1146.2006.00415 [18] 王盛利, 李士国, 倪晋麟, 等. 一种新的变换—匹配傅里叶变换[J]. 电子学报, 2001, 29(3): 403–405. doi: 10.3321/j.issn:0372-2112.2001.03.030WANG Shengli, LI Shiguo, NI Jinlin, et al. A new transform—match Fourier transform[J]. Acta Electronica Sinica, 2001, 29(3): 403–405. doi: 10.3321/j.issn:0372-2112.2001.03.030 -





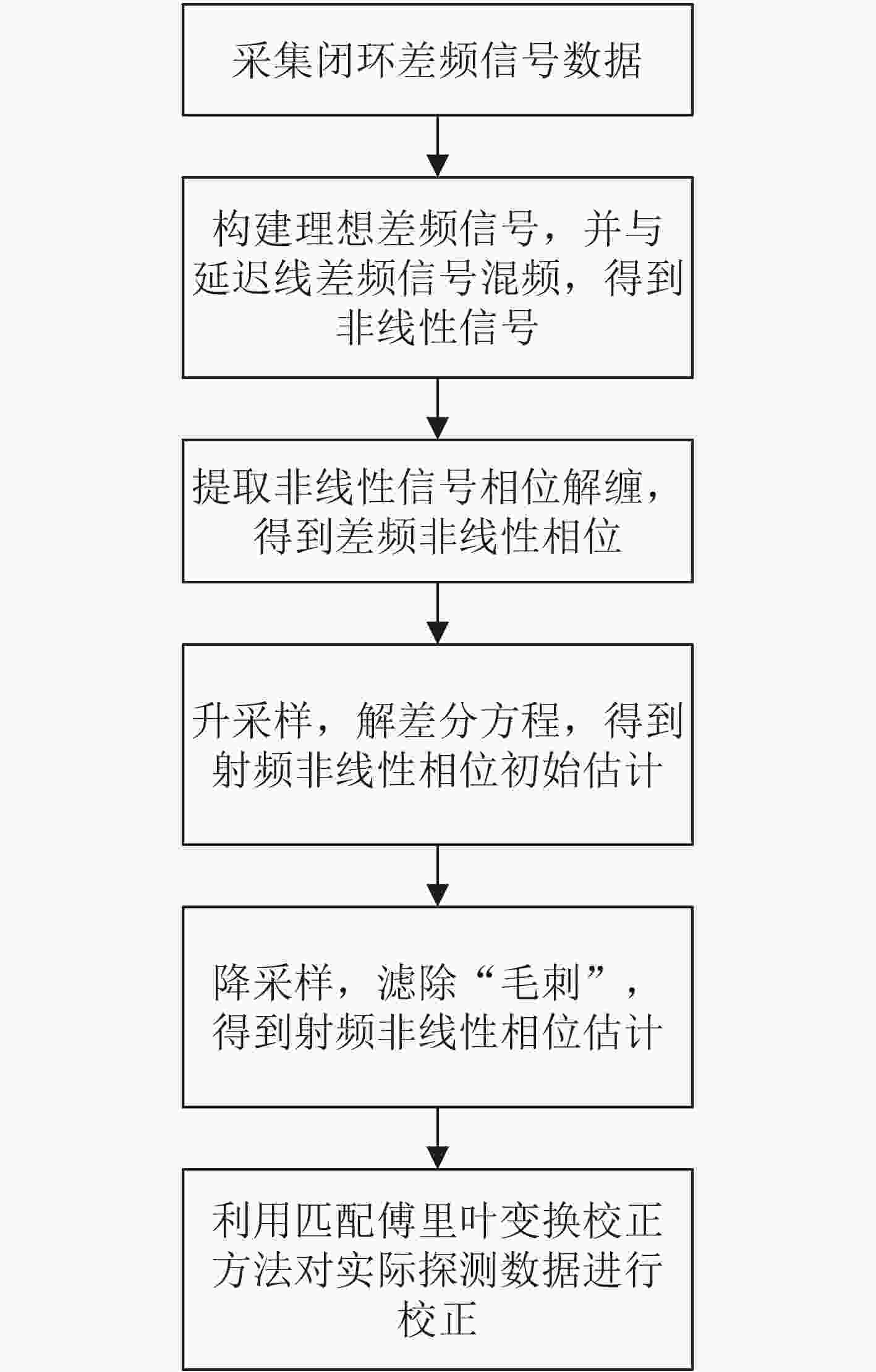
 下载:
下载:





 下载:
下载:
