Atrial Fibrillation Detection Based on Hilbert-Huang Transform and Deep Convolutional Neural Network
-
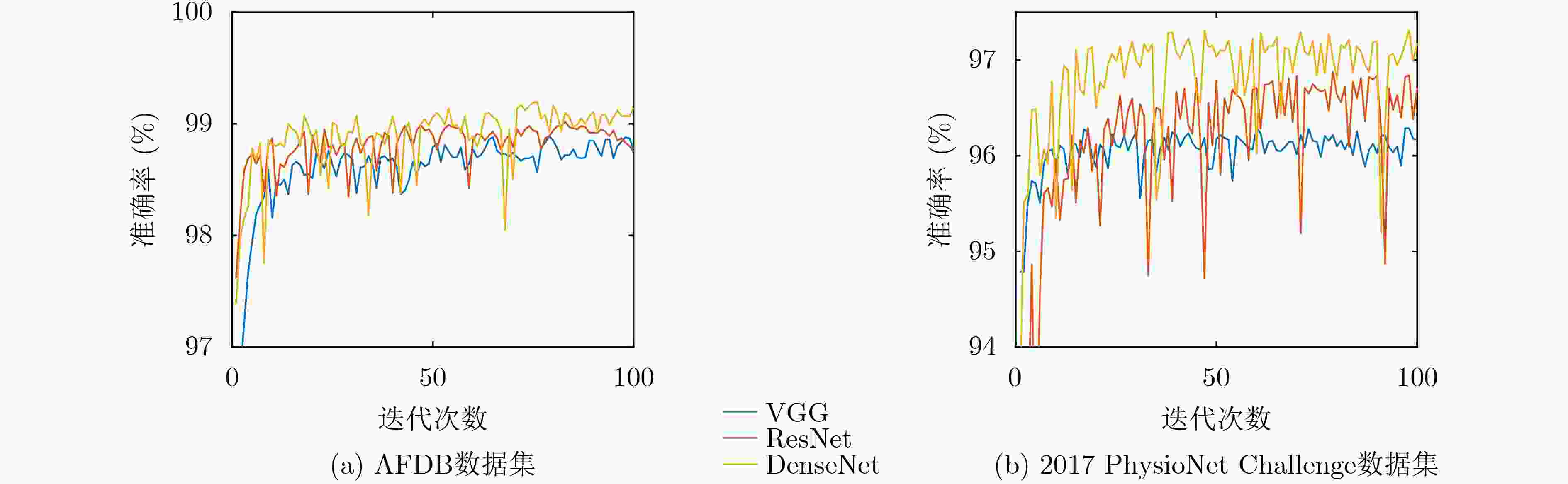
摘要: 房颤是一种常见的心律失常,其发病率会随着年龄增长而升高。因此,从心电(ECG)信号中尽早识别出房颤,有助于降低中风风险和心源性死亡率。为有效提高其检测准确率,该文提出一种基于希尔伯特黄变换(HHT)和深度卷积神经网络的房颤检测方法。1维的时域心电信号通过希尔伯特黄变换,转换为时频域信号,旨在通过时频分析,丰富原始信号的特征。进而,采用DenseNet深度卷积神经网络来处理精细的时频图,并在迭代过程中选出最佳检测模型。该方法获得的最佳检测模型在麻省理工学院-贝斯以色列医院(MIT-BIH)和2017年生理信号竞赛(2017 PhysioNet Challenge)的房颤数据集上分别取得了99.11%和97.25%的检测准确率。此外,该文将希尔伯特黄变换与其他时频分析方法以及稠密网络(DenseNet)与其他卷积神经网络进行了对比。相比于其他检测方法,实验结果表明希尔伯特黄变换和深度卷积神经网络(DCNN)为房颤检测提供了更加准确的识别方式。Abstract: Atrial fibrillation is a common arrhythmia and its morbidity increases with age. Thus, stroke risk and cardiogenic mortality can be significantly reduced by early atrial fibrillation detection from ElectroCardioGram (ECG). In order to improve effectively detection accuracy, a novel approach is proposed to detect atrial fibrillation based on Hilbert-Huang Transform(HHT) and deep convolutional neural network. HHT is employed to transform electrocardiogram from time domain to time-frequency domain so as to enrich the feature of original data. Following that, DenseNet is introduced to deal with the detailed graph and the best model is selected during the iteration. The optimal model obtained by the proposed method achieves 99.11% and 97.25% accuracy respectively on the Massachusetts Institute of Technology - Beth Israel Hospital(MIT-BIH) and 2017 PhysioNet Challenge atrial fibrillation databases. In addition, HHT and DenseNet are compared with other time-frequency analysis and convolutional neural networks, respectively. Compared with some existing methods, the results proved that atrial fibrillation detection by HHT and Deep Convolutional Neural Network(DCNN) obtains a high detection performance.
-
表 1 EMD算法步骤
步骤 1 $r(t) = x(t)$ 步骤 2 $ s(t) = r(t) $ 步骤 3 求$ s(t) $的极大值和极小值。 步骤 4 根据极大极小值分别计算上包络线$ {e_{\max }}(t) $和下包络线$ {e_{\min }}(t) $。 步骤 5 计算两个包络线的均线$ m(t) = $$ [{e_{\max }}(t){\text{ + }}{e_{\min }}(t)]/2 $。 步骤 6 计算$ h(t) = r(t) - m(t) $。如果$ h(t) $满足上述两个限制,则$ h(t) $为其中一个IMF,否则令$ s(t) = r(t) - h(t) $返回步骤3。 步骤 7 计算$ r(t) = r(t) - s(t) $,如果${{r}}(t)$有超过两个极值点,返回步骤2去计算另一个IMF,否则分解结束。 表 2 DenseNet结构
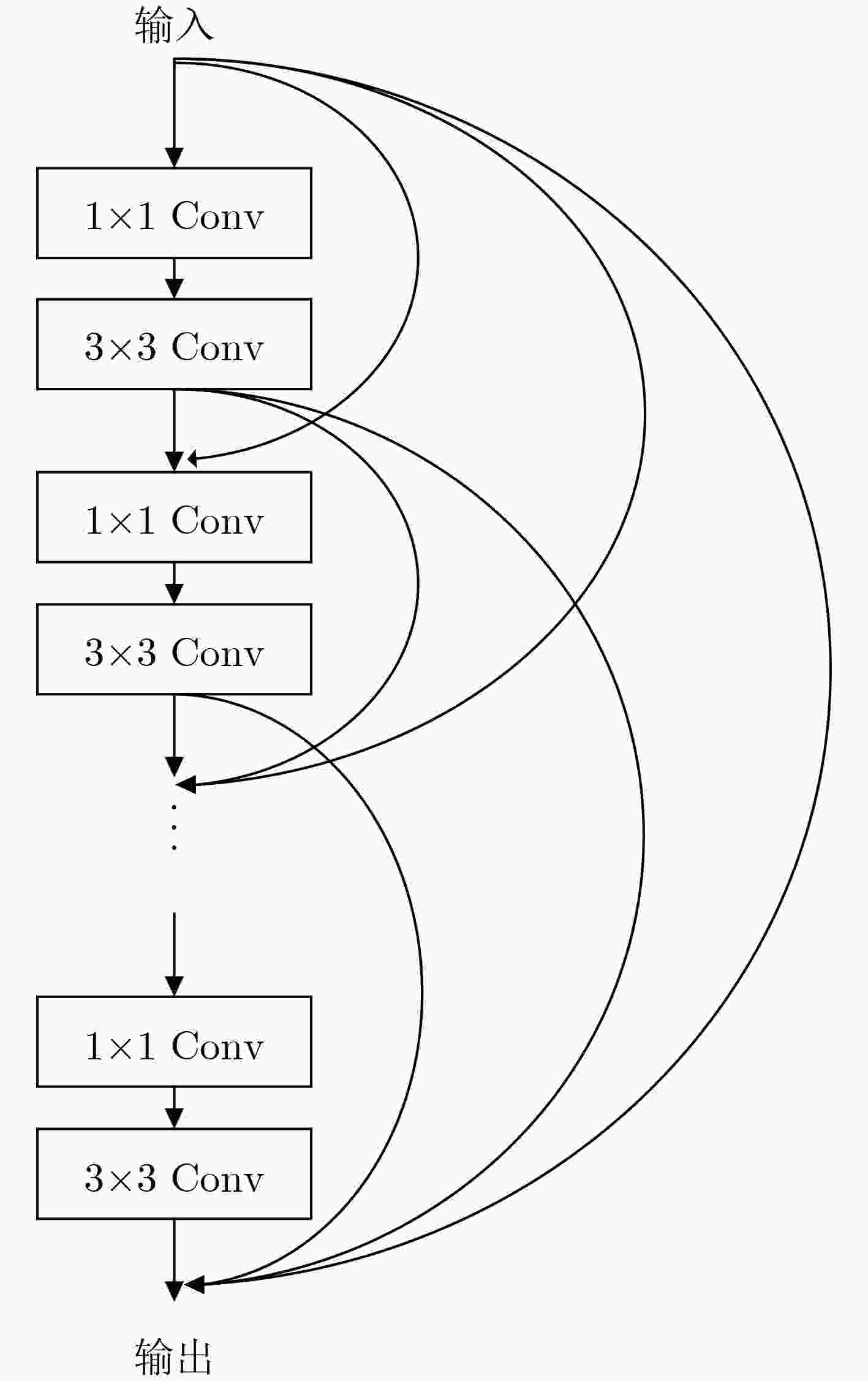
层 输出特征图 结构 Conv1 48×623 7×7 conv, 64, stride=2, padding=1 Pool1 24×312 2×2 max pool Dense Block1 24×312 $\left[ {\begin{array}{*{20}{c}} {{\text{1}} \times {\text{1}}\;{\text{conv}},\;128} \\ {3 \times 3\;{\text{conv,}}\;32,{\text{ padding = 1}}} \end{array}} \right] \times 6$ Conv2 24×312 1×1 conv, 128 Pool2 12×156 2×2 avg pool Dense Block2 12×156 $ \left[ {\begin{array}{*{20}{c}} {{\text{1}} \times {\text{1}}\;{\text{conv}},\;128} \\ {3 \times 3\;{\text{conv,}}\;32,{\text{ padding = 1}}} \end{array}} \right] \times 12 $ Conv3 12×156 1×1 conv, 256 Pool3 6×78 2×2 avg pool Dense Block3 6×78 $\left[ {\begin{array}{*{20}{c}} {{\text{1}} \times {\text{1}}\;{\text{conv}},\;128} \\ {3 \times 3\;{\text{conv,}}\;32,{\text{ padding = 1}}} \end{array}} \right] \times 32$ Conv4 6×78 1×1 conv, 640 Pool4 3×39 2×2 avg pool Dense Block4 3×39 $\left[ {\begin{array}{*{20}{c}} {{\text{1}} \times {\text{1}}\;{\text{conv}},\;128} \\ {3 \times 3\;{\text{conv,}}\;32,{\text{ padding = 1}}} \end{array}} \right] \times 32$ Pool1 1×1 3×39 avg pool flatten 1×1664 Fully connected layer 1×2 表 3 AFDB数据集
训练集 验证集 测试集 总计 房颤 24413 3052 3051 30516 窦性节律 56224 7028 7028 70280 总计 80637 10080 10079 100796 表 4 2017 PhysioNet Challenge数据集
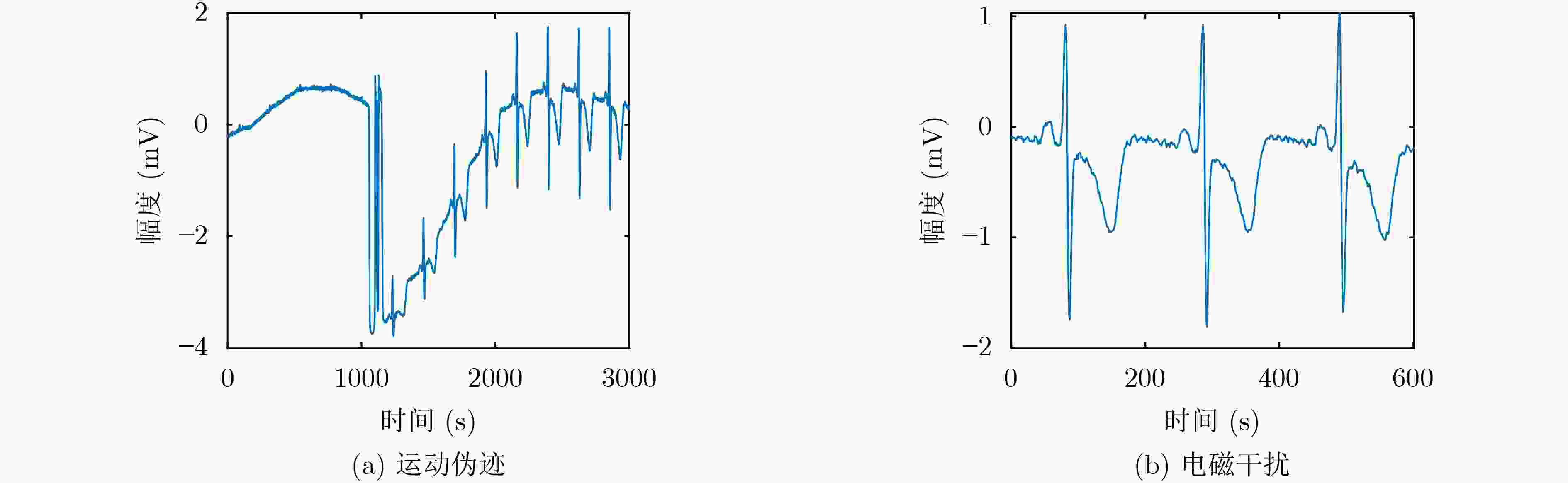
训练集 验证集 测试集 总计 房颤 4383 548 548 5479 窦性节律 30012 3752 3751 37515 总计 34395 4300 4299 42994 表 5 运动伪迹时模型鲁棒性验证(%)
对比算法 ACC SP SE 本文 77.40 84.62 70.37 随机森林 60.38 57.69 62.96 支持向量机 56.60 53.85 59.26 Adaboost 62.26 61.54 62.96 表 6 电磁干扰时模型鲁棒性验证(%)
对比算法 ACC SP SE 本文 97.85 98.04 97.62 随机森林 93.91 93.46 94.44 支持向量机 87.81 89.29 86.33 Adaboost 91.40 92.86 89.93 表 7 不同算法的性能比较(%)
-
[1] YOUNG M. Atrial fibrillation[J]. Critical Care Nursing Clinics of North America, 2019, 31(1): 77–90. doi: 10.1016/j.cnc.2018.11.005 [2] HENDRIKS J M L and HEIDBÜCHEL H. The management of atrial fibrillation: An integrated team approach–insights of the 2016 European Society of Cardiology guidelines for the management of atrial fibrillation for nurses and allied health professionals[J]. European Journal of Cardiovascular Nursing, 2019, 18(2): 88–95. doi: 10.1177/1474515118804480 [3] KIRCHHOF P, BENUSSI S, KOTECHA D, et al. 2016 ESC Guidelines for the management of atrial fibrillation developed in collaboration with EACTS[J]. Kardiol Pol, 2016, 74(12): 1359–1469. doi: 10.5603/KP.2016.0172 [4] FREEDMAN B, CAMM J, CALKINS H, et al. Screening for atrial fibrillation: A report of the AF-SCREEN international collaboration[J]. Circulation, 2017, 135(19): 1851–1867. doi: 10.1161/CIRCULATIONAHA.116.026693 [5] LAI Dakun, ZHANG Xinshu, ZHANG Yifei, et al. Convolutional neural network based detection of atrial fibrillation combing R-R intervals and F-wave frequency spectrum[C]. The 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 2019: 4897–4900. [6] DUNCKER D, DING W Y, ETHERIDGE S, et al. Smart wearables for cardiac monitoring—real-world use beyond atrial fibrillation[J]. Sensors, 2021, 21(7): 2539. doi: 10.3390/s21072539 [7] EBRAHIMZADEH E, KALANTARI M, JOULANI M, et al. Prediction of paroxysmal Atrial Fibrillation: A machine learning based approach using combined feature vector and mixture of expert classification on HRV signal[J]. Computer Methods and Programs in Biomedicine, 2018, 165: 53–67. doi: 10.1016/j.cmpb.2018.07.014 [8] MOHEBBI M and GHASSEMIAN H. Prediction of paroxysmal atrial fibrillation based on non-linear analysis and spectrum and bispectrum features of the heart rate variability signal[J]. Computer Methods and Programs in Biomedicine, 2012, 105(1): 40–49. doi: 10.1016/j.cmpb.2010.07.011 [9] ACHARYA U R, FUJITA H, LIH O S, et al. Automated detection of arrhythmias using different intervals of tachycardia ECG segments with convolutional neural network[J]. Information Sciences, 2017, 405: 81–90. doi: 10.1016/j.ins.2017.04.012 [10] 蒋芳芳, 徐敬傲, 李任, 等. 基于CNN的心冲击信号阵发性房颤自动检测方法[J]. 东北大学学报:自然科学版, 2019, 40(11): 1539–1542,1548. doi: 10.12068/j.issn.1005-3026.2019.11.004JIANG Fangfang, XU Jing’ao, LI Ren, et al. Automatic detection method of paroxysmal atrial fibrillation for ballistocardiagram based on CNN[J]. Journal of Northeastern University:Natural Science, 2019, 40(11): 1539–1542,1548. doi: 10.12068/j.issn.1005-3026.2019.11.004 [11] PETMEZAS G, HARIS K, STEFANOPOULOS L, et al. Automated atrial fibrillation detection using a hybrid CNN-LSTM network on imbalanced ECG datasets[J]. Biomedical Signal Processing and Control, 2021, 63: 102194. doi: 10.1016/j.bspc.2020.102194 [12] 杨萍, 王丹, 康子健, 等. 基于模式识别和集成CNN-LSTM的阵发性房颤预测模型[J]. 浙江大学学报:工学版, 2020, 54(5): 1039–1048. doi: 10.3785/j.issn.1008-973X.2020.05.023YANG Ping, WANG Dan, KANG Zijian, et al. Prediction model of paroxysmal atrial fibrillation based on pattern recognition and ensemble CNN-LSTM[J]. Journal of Zhejiang University:Engineering Science, 2020, 54(5): 1039–1048. doi: 10.3785/j.issn.1008-973X.2020.05.023 [13] 顾佳艳, 蒋明峰, 李杨, 等. 基于多头注意力机制的房颤检测方法[J]. 计算机系统应用, 2021, 30(4): 17–24. doi: 10.15888/j.cnki.csa.007885GU Jiayan, JIANG Mingfeng, LI Yang, et al. Atrial fibrillation detection using multi-head attention mechanism[J]. Computer Systems &Applications, 2021, 30(4): 17–24. doi: 10.15888/j.cnki.csa.007885 [14] FAN Xiaomao, YAO Qihang, CAI Yunpeng, et al. Multiscaled fusion of deep convolutional neural networks for screening atrial fibrillation from single lead short ECG recordings[J]. IEEE Journal of Biomedical and Health Informatics, 2018, 22(6): 1744–1753. doi: 10.1109/JBHI.2018.2858789 [15] XIA Yong, WULAN Naren, WANG Kuanquan, et al. Detecting atrial fibrillation by deep convolutional neural networks[J]. Computers in Biology and Medicine, 2018, 93: 84–92. doi: 10.1016/j.compbiomed.2017.12.007 [16] MA Caiyun, WEI Shoushui, CHEN Tongshuai, et al. Integration of results from convolutional neural network in a support vector machine for the detection of atrial fibrillation[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 70: 2504610. doi: 10.1109/TIM.2020.3044718 [17] 杨淑莹, 桂彬彬, 陈胜勇. 基于小波分解和1D-GoogLeNet的心律失常检测[J]. 电子与信息学报, 2021, 43(10): 3018–3027. doi: 10.11999/JEIT200774YANG Shuying, GUI Binbin, and CHEN Shengyong. Arrhythmia detection based on wavelet decomposition and 1D-GoogLeNet[J]. Journal of Electronics &Information Technology, 2021, 43(10): 3018–3027. doi: 10.11999/JEIT200774 [18] HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903–995. doi: 10.1098/rspa.1998.0193 [19] HUANG Gao, LIU Zhuang, VAN DER MAATEN L, et al. Densely connected convolutional networks[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, New York, USA, 2017: 2261–2269. [20] 杨永春, 廖红英, 尹晓姝. 远程心电监测系统在阵发性房颤监测中的应用价值[J]. 检验医学与临床, 2021, 18(19): 2824–2826. doi: 10.3969/j.issn.1672-9455.2021.19.010YANG Yongchun, LIAO Hongying, and YIN Xiaoshu. Application value of remote ECG monitoring system in monitoring paroxysmal atrial fibrillation[J]. Laboratory Medicine and Clinic, 2021, 18(19): 2824–2826. doi: 10.3969/j.issn.1672-9455.2021.19.010 [21] 胡振原, 刘澄玉, 李建清. 一种可消除运动伪迹的可穿戴心电监测系统[J]. 电子测量技术, 2020, 43(15): 72–78. doi: 10.19651/j.cnki.emt.2004492HU Zhenyuan, LIU Chengyu, and LI Jianqing. Wearable ECG detection system for eliminating motion artifacts[J]. Electronic Measurement Technology, 2020, 43(15): 72–78. doi: 10.19651/j.cnki.emt.2004492 [22] MOODY G B and MARK R R. A new method for detecting atrial fibrillation using R-R intervals[J]. Computers in Cardiology, 1983, 10: 227–230. [23] GOLDBERGER A L, AMARAL L A N, GLASS L, et al. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals[J]. Circulation, 2000, 101(23): e215–e220. doi: 10.1161/01.CIR.101.23.e215 [24] SIMONYAN K and ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]. The 3rd International Conference on Learning Representations, San Diego, USA, 2015. [25] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. [26] JIN Yanrui, QIN Chengjin, HUANG Yixiang, et al. Multi-domain modeling of atrial fibrillation detection with twin attentional convolutional long short-term memory neural networks[J]. Knowledge-Based Systems, 2020, 193: 105460. doi: 10.1016/j.knosys.2019.105460 [27] JIN Yanrui, QIN Chengjin, LIU Jinlei, et al. A novel domain adaptive residual network for automatic atrial fibrillation detection[J]. Knowledge-Based Systems, 2020, 203: 106122. doi: 10.1016/j.knosys.2020.106122 [28] FAUST O, SHENFIELD A, KAREEM M, et al. Automated detection of atrial fibrillation using long short-term memory network with RR interval signals[J]. Computers in Biology and Medicine, 2018, 102: 327–335. doi: 10.1016/j.compbiomed.2018.07.001 [29] MA Fengying, ZHANG Jingyao, CHEN Wei, et al. An automatic system for atrial fibrillation by using a CNN-LSTM Model[J]. Discrete Dynamics in Nature and Society, 2020, 2020: 3198783. doi: 10.1155/2020/3198783 [30] ANDERSEN R S, PEIMANKAR A, and PUTHUSSERYPADY S. A deep learning approach for real-time detection of atrial fibrillation[J]. Expert Systems with Applications, 2019, 115: 465–473. doi: 10.1016/j.eswa.2018.08.011 [31] BEHAR J A, ROSENBERG A A, YANIV Y, et al. Rhythm and quality classification from short ECGs recorded using a mobile device[C]. 2017 Computing in Cardiology (CinC), Rennes, France, 2017, doi: 10.22489/CinC.2017.165-056. [32] LIMAM M and PRECIOSO F. Atrial fibrillation detection and ECG classification based on convolutional recurrent neural network[C]. 2017 Computing in Cardiology (CinC), Rennes, France, 2017, doi: 10.22489/CinC.2017.171-325. -





 下载:
下载:


 下载:
下载:
