Related-Tweak Multiple Impossible Differential Attack for TweAES
-
摘要: TweAES算法是在NIST轻量级密码标准竞赛中,进入到第2轮的认证加密候选算法。该文提出了对8轮TweAES算法的相关调柄多重不可能差分攻击。首先,利用两类不可能差分区分器,构造了两条攻击路径,每条攻击路径需要攻击16 Byte子密钥。值得注意的是,两条攻击路径有相同的明文结构和14 Byte的公共子密钥,攻击者可以利用同一个明文结构下的明文对,筛选两次错误子密钥,且因为有大量的公共子密钥,可以提高子密钥筛选的效率。此外,利用密钥生成算法的不完全性,有针对性地选择子密钥字节。利用子密钥之间的相关性,提高主密钥恢复效率,从而改进整体攻击方案的结果。与前人的分析结果相比较,该文对8轮TweAES的攻击方案在时间、数据、存储3项复杂度结果上均有所改进。Abstract: TweAES is one of the second-round candidates in the NIST Lightweight Cryptography Standardization competition. The related-tweak multiple impossible differentials attack of 8-round TweAES is presented. Firstly, two types of impossible differential distinguishers are utilized to construct two attack trails, and each attack trail needs to guess 16 Byte subkey. It is worth noting that two attack trails have the same plaintext structure and 14 Byte common subkey. Attackers can utilize the plaintext pairs with the same plaintext structure to reject wrong subkeys by two filters processed, and because of a large number of common subkey, the efficiency of subkeys sifting can be improved. Furthermore, the incompleteness of the key schedule is utilized to choose the subkey Bytes. With the help of the relations of subkey Bytes, the efficiency of reconstructing the corresponding master keys can be improved, so the complexity of the whole attack scheme can be improved. Compared with the previous results, this work obtain the new attack scheme of 8-round TweAES, which needs lower time, data, and memory complexities than other attack schemes.
-
Key words:
- Lightweight cipher /
- Impossible differential /
- TweAES /
- Tweak
-
表 1 符号说明
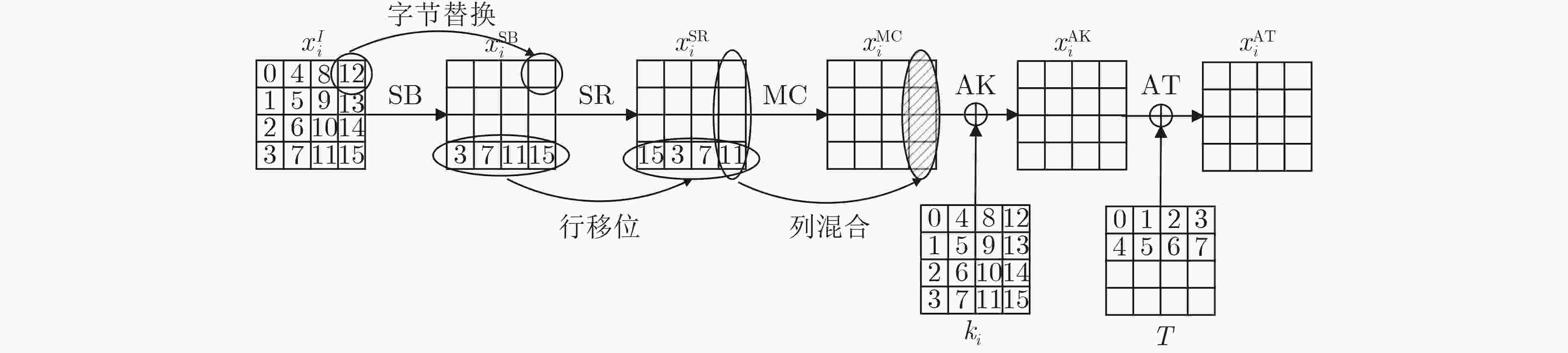
符号 意义 $ P $ 明文 $ C $ 密文 $x_{i,(p,\cdots,r)}^{{\rm{I/SB/SR/MC/AK/AT}}}$ 第$ i $轮输入/字节替换/行移位变换/混合变换/轮密钥加/调柄加后的第$(p, \cdots ,r)$ Byte值 $\Delta x$ $x$的差分值 ${k_{i,(p,\cdots,r)} }$ 第$ i $轮子密钥${k_i}$的第$(p, \cdots ,r)$ Byte值 $a{\not \to _{i - {\rm{round}}} }b$ 差分$ a $经$ i $轮加密后不能得到差分$ b $ 表 2 TweAES的8个6轮相关调柄不可能差分区分器
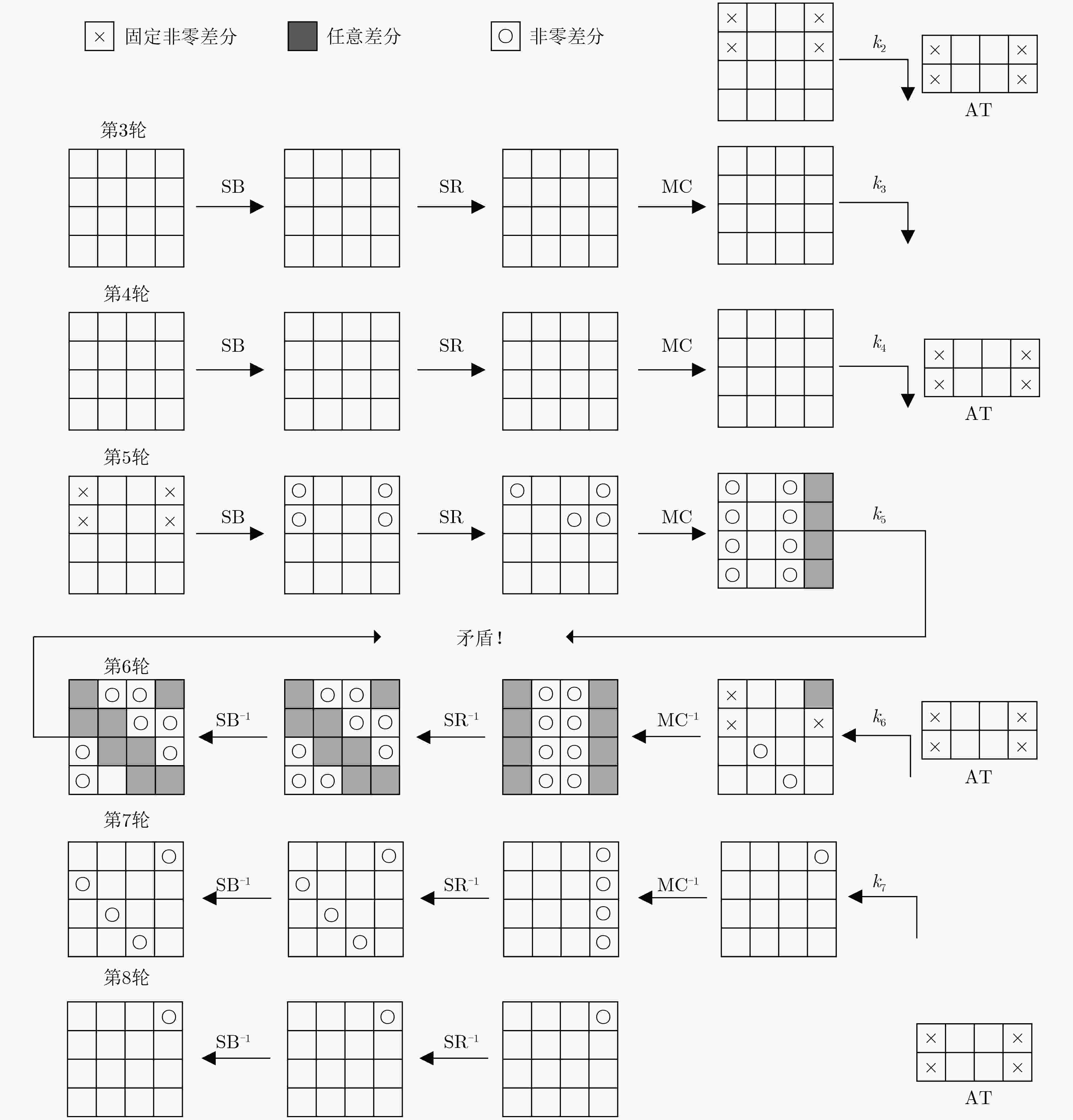
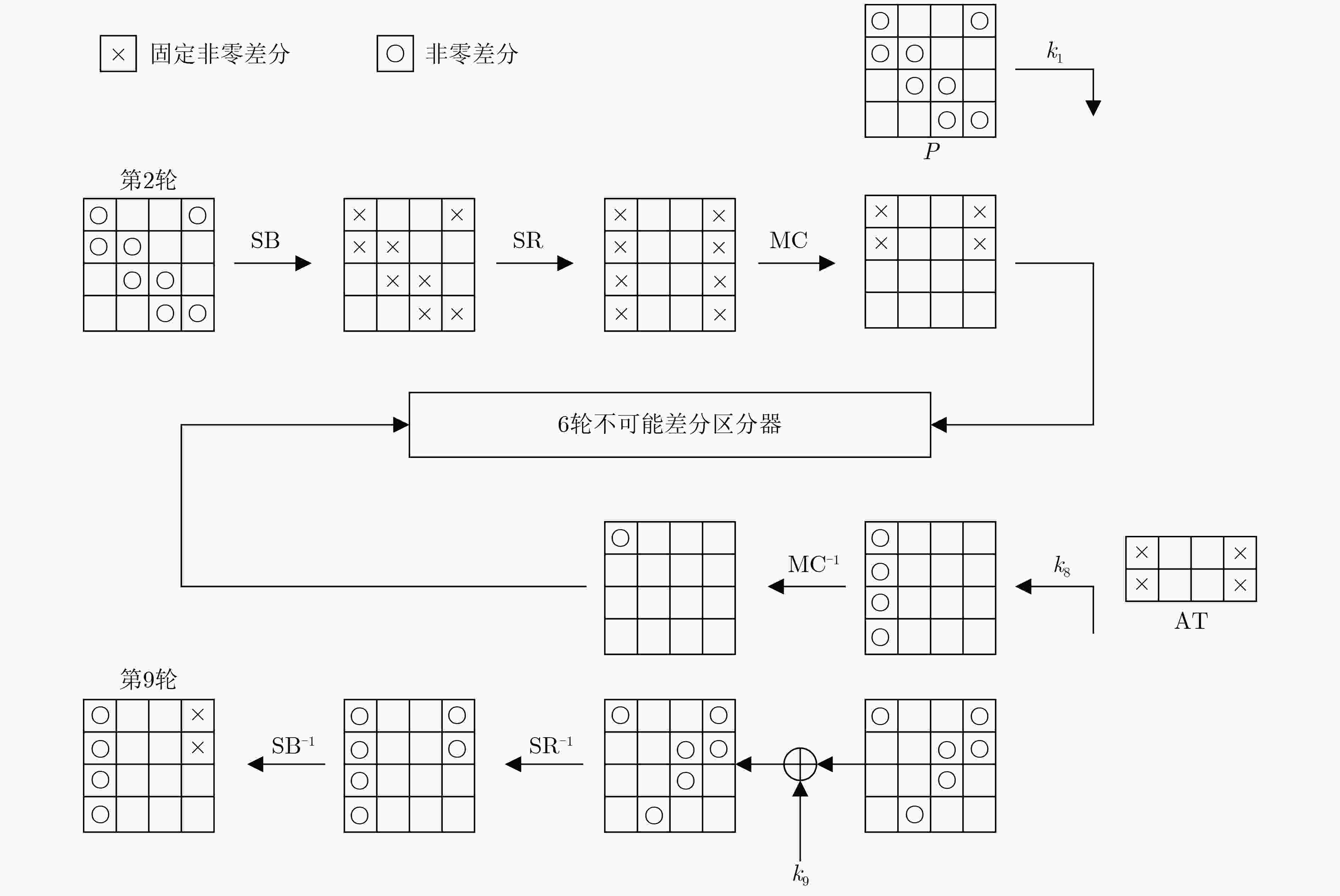
类别 序号 区分器的输入差分(具体差分值) 区分器的输入差分(截断差分值) 一 1 (a,a,0,0,0,0,0,0,0,0,0,0,a,a,0,0) (0,0,0,0,0,0,0,0,0,0,0,0,*,0,0,0) 2 (0,0,0,0,0,0,0,0,0,0,0,0,0,*,0,0) 3 (0,0,0,0,0,0,0,0,0,0,0,0,0,0,*,0) 4 (0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,*) 二 5 (*,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0) 6 (0,*,0,0,0,0,0,0,0,0,0,0,0,0,0,0) 7 (0,0,*,0,0,0,0,0,0,0,0,0,0,0,0,0) 8 (0,0,0,*,0,0,0,0,0,0,0,0,0,0,0,0) 注:a为8 bit具体值0x01,*为8 bit任意非零值。主调柄差分值为(1001)。 表 3 AES-128中第9轮子密钥后12 Byte与第1轮子密钥关联
密钥字节 关联字节 密钥字节 关联字节 密钥字节 关联字节 4 A16\{0,2,8,10} 8 A16\{0,1,4} 12 A16\{0,1,2,4,5,8,10} 5 A16\{1,3,9,11} 9 A16\{1,2,5} 13 A16\{1,2,3,5,6,9,11} 6 A16\{0,2,8,10} 10 A16\{2,3,6} 14 A16\{0,2,3,6,7,8,10} 7 A16\{1,3,9,11} 11 A16\{0,3,7} 15 A16\{0,1,3,4,7,9,11} 注:密钥字节为第9轮子密钥字节位置,A16代表全部16 Byte,关联字节指与第1轮子密钥字节的关联:如$ {k_{9, (4)}} $与4 Byte子密钥$ {k_{1, (0,2,8,10)}} $无关,只需要知道子密钥$ {k_1} $其余的12 Byte,即可由AES-128的密钥生成算法得到。 表 4 TweAES的攻击结果
-
[1] CHAKRABORTI A, DATTA N, JHA A, et al. ESTATE: A lightweight and low energy authenticated encryption mode[J]. IACR Transactions on Symmetric Cryptology, 2020, 2020(S1): 350–389. doi: 10.13154/tosc.v2020.iS1.350-389 [2] DWORKIN M J, BARKER E B, NECHVATAL J R, et al. Advanced encryption standard (AES)[EB/OL]. https: //doi. org/https://doi.org/10.6028/NIST.FIPS.197, 2001. [3] BIHAM E, BIRYUKOV A, and SHAMIR A. Cryptanalysis of Skipjack reduced to 31 rounds using impossible differentials[C]. Proceedings of International Conference on the Theory and Applications of Cryptographic Techniques, Czech Republic, 1999: 12-23. [4] AOKI K, ICHIKAWA T, KANDA M, et al. Camellia: A 128-bit block cipher suitable for multiple platforms — design andanalysis[C]. Proceedings of the 7th Annual International Workshop on Selected Areas in Cryptography, Ontario, Canada, 2000: 39-56. [5] TSUNOO Y, TSUJIHARA E, SHIGERI M, et al. Cryptanalysis of CLEFIA using multiple impossible differentials[C]. Proceedings of 2008 International Symposium on Information Theory and Its Applications, Auckland, New Zealand, 2008: 1-6. [6] BOURA C, NAYA-PLASENCIA M, and SUDER V. Scrutinizing and improving impossible differential attacks: Applications to CLEFIA, Camellia, LBlock and Simon[C]. Proceedings of the 20th International Conference on the Theory and Application of Cryptology and Information Security, Kaoshiung, China, 2014: 179-199. [7] BOURA C, LALLEMAND V, NAYA-PLASENCIA M, et al. Making the impossible possible[J]. Journal of Cryptology, 2018, 31(1): 101–133. doi: 10.1007/s00145-016-9251-7 [8] LI Xinran, JIN Chenhui, and FU Fangwei. Improved results of impossible differential cryptanalysis on reduced FOX[J]. The Computer Journal, 2016, 59(4): 541–548. doi: 10.1093/comjnl/bxv073 [9] LI Xinran, FU Fangwei, and GUANG Xuan. Multiple impossible differential cryptanalysis on reduced FOX[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2015, 98(3): 906–911. doi: 10.1587/transfun.E98.A.906 [10] SHIRAI T, SHIBUTANI K, AKISHITA T, et al. The 128-bit blockcipher CLEFIA (extended abstract)[C]. Proceedings of the 14th International Workshop on Fast Software Encryption, Luxembourg, 2007: 181-195. [11] WU Wenling and ZHANG Lei. LBlock: A lightweight block cipher[C]. Proceedings of the 9th International Conference on Applied Cryptography and Network Security, Nerja, Spain, 2011: 327-344. [12] JUNOD P and VAUDENAY S. FOX: A new family of block ciphers[C]. Proceedings of the 11th International Workshop on Selected Areas in Cryptography, Waterloo, Canada, 2004: 114-129. [13] BONNETAIN X, NAYA-PLASENCIA M, and SCHROTTENLOHER A. Quantum security analysis of AES[J]. IACR Transactions on Symmetric Cryptology, 2019, 2019(2): 55–93. doi: 10.13154/tosc.v2019.i2.55-93 [14] GILBERT H. A simplified representation of AES[C]. Proceedings of the 20th International Conference on the Theory and Application of Cryptology and Information Security, Kaoshiung, China, 2014: 200-222. [15] MALA H, DAKHILALIAN M, RIJMEN V, et al. Improved impossible differential cryptanalysis of 7-round AES-128[C]. Proceedings of the 11th International Conference on Cryptology in India, Hyderabad, India, 2010: 282-291. [16] SUN Siwei, GERAULT D, LAFOURCADE P, et al. Analysis of AES, SKINNY, and others with constraint programming[J]. IACR Transactions on Symmetric Cryptology, 2017, 2017(1): 281–306. doi: 10.13154/tosc.v2017.i1.281-306 [17] CUI Ting, JIN Chenhui, ZHANG Bin, et al. Searching all truncated impossible differentials in SPN[J]. IET Information Security, 2017, 11(2): 89–96. doi: 10.1049/iet-ifs.2015.0052 [18] 张海青. AES型密钥编排方案扩散不完全性的研究及应用[D]. [硕士论文], 战略支援部队信息工程大学, 2019.ZHANG Haiqing. Research and application of incomplete diffusion of AES-like key schedule[D]. [Master dissertation], Information Engineering University, 2019. [19] LEURENT G and PERNOT C. New representations of the AES key schedule[C]. Proceedings of the 40th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 2021: 54-84. [20] NIU Chao, LI Muzhou, WANG Meiqin, et al. Related-tweak impossible differential cryptanalysis of reduced-round TweAES[C]. Proceedings of the 28th International Conference on Selected Areas in Cryptography, Cham, Switzerland, 2021: 223-245. -





 下载:
下载:


 下载:
下载:
